Self-interference Digital Cancellation Algorithm in Simultaneous Transceiver System Based on Deep Neural Network
-
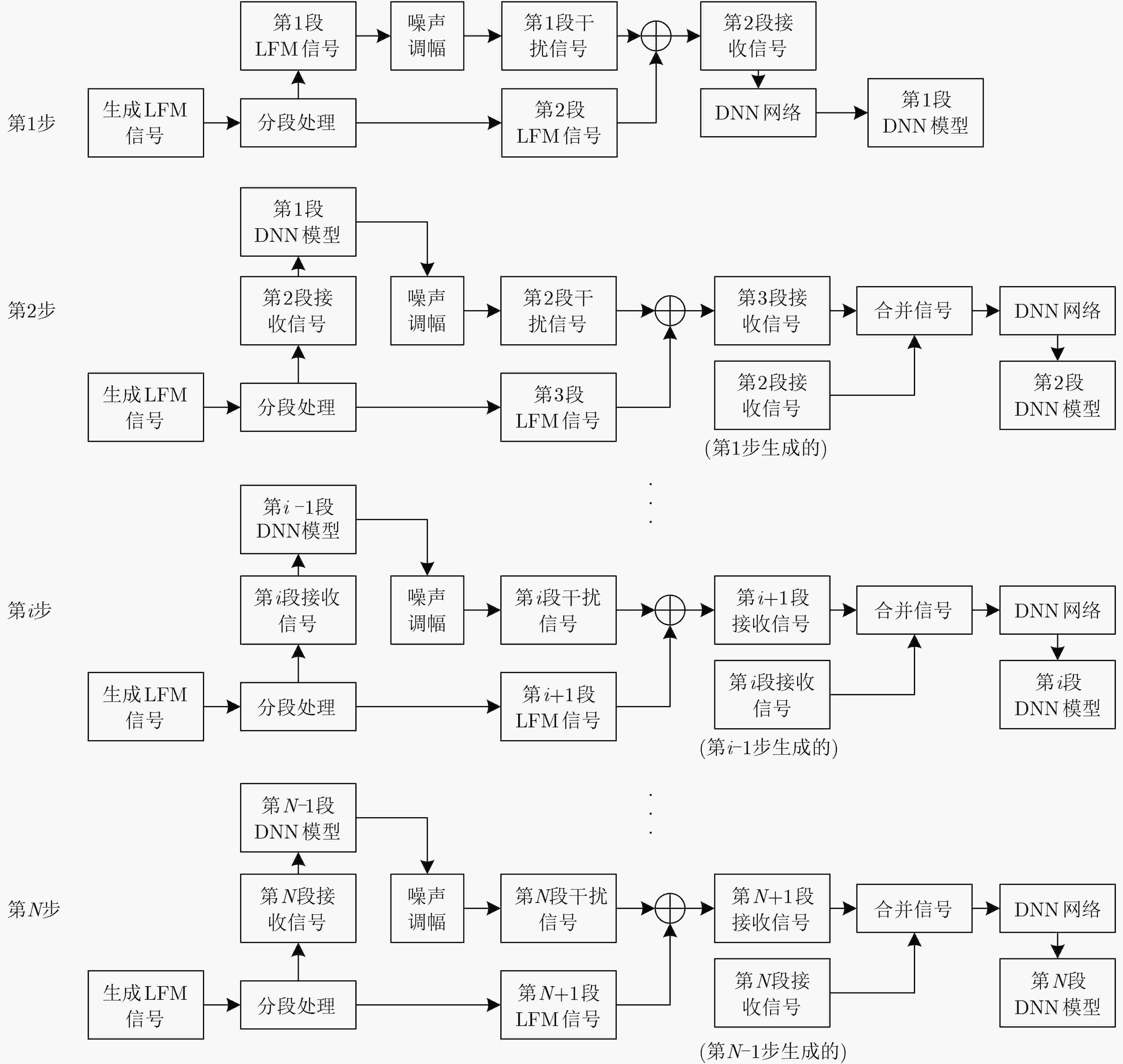
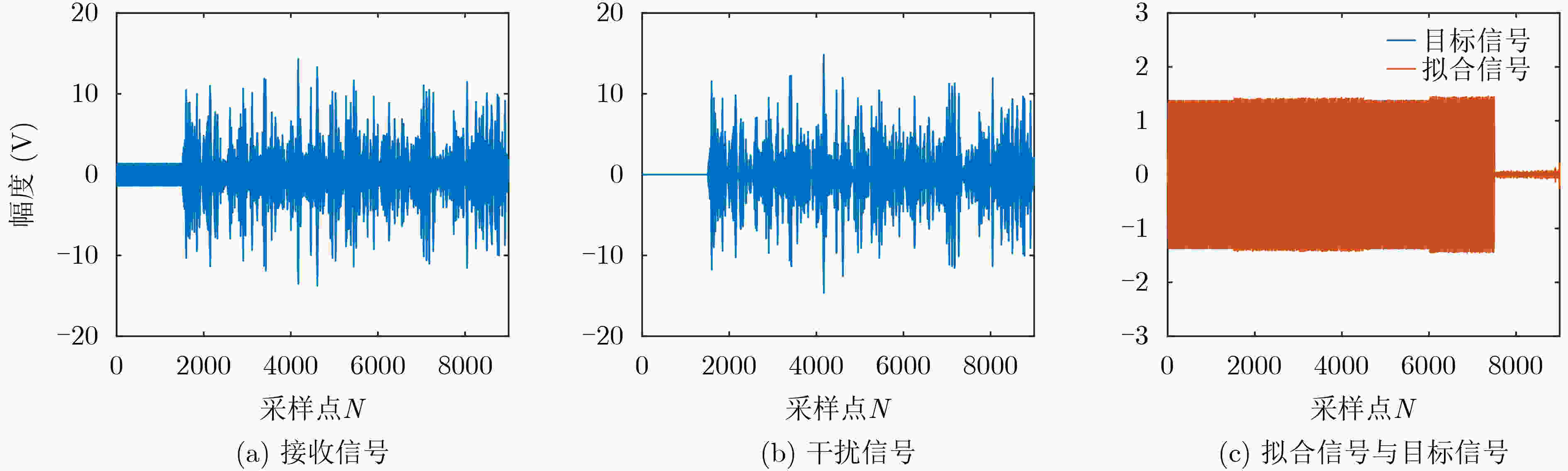
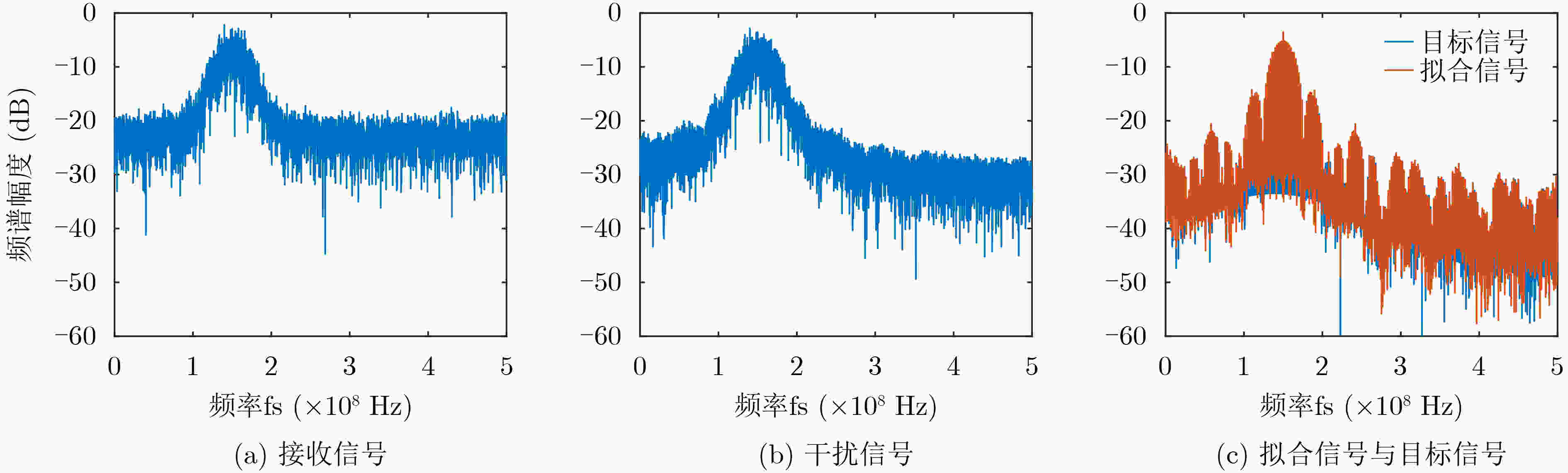
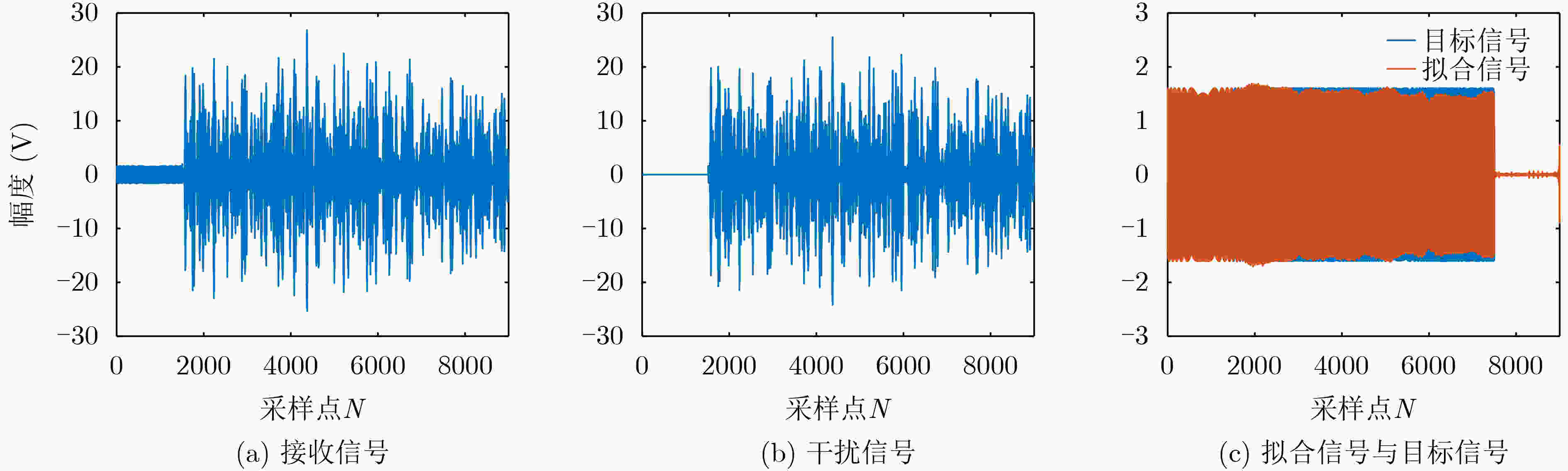
摘要: 为了解决转发式干扰机收发同时系统中的自干扰难以对消问题,该文设计一种基于深度神经网络(DNN)的自干扰对消算法。在自干扰信号与目标信号强相关且混叠的情况下该算法可以有效地消除自干扰信号。在此基础上,该文利用分段侦收的信号快速生成干扰的方法,验证了该算法在收发同时系统中自干扰信号对消的可行性,实现了基于本脉冲的雷达干扰信号构建,对敌方雷达快速做出反应,在电子对抗中占据有利地位。该文利用典型的线性调频(LFM)和二进制相移键控(BPSK)雷达信号生成数据集训练深度神经网络,用测试集去测试网络输出的模型。实验结果表明:在收发同时系统中目标信号与自干扰信号混叠的情况下,基于DNN的自干扰对消算法可以有效消除自干扰信号,在信干比–8 dB的情况下,对消比可达到26 dB以上。Abstract: In order to solve the problem that the self-interference is difficult to eliminate in the transceiver system of the repeater jammer, a self-interference cancellation algorithm based on Deep Neural Network(DNN) is presented in this paper. This proposed algorithm can effectively eliminate the self-interference signal when the self-interference signal is correlated and mixed with the target signal. On this basis, the interference generation method of segmenting interception is used in this paper, which verifies the feasibility of jamming signal cancellation in the simultaneous transceiver system. It realizes the construction of radar jamming signal considering the pulse, which can quickly respond to enemy radars and occupy a favorable position in electronic countermeasures. In this paper, a typical Linear Frequency Modulation(LFM) and Binary Phase Shift Keying (BPSK) radar signal are used to generate a data set to train the DNN network, and the test set is used to test the output model of the network. The experimental results show that the self-interference cancellation algorithm based on DNN can effectively eliminate the self-interference signal when the target signal and self-interference signal are mixed in the simultaneous transceiver system, and the cancellation ratio can reach more than 26 dB when the signal to interference ratio is –8 dB.
-
表 1 信号的调制参数
信号形式 载频${f_c}$(MHz) 带宽$B$(MHz) 初相位$\varphi $ 幅度$A$ 信干比(dB) 训练集 LFM信号 100~200 20~40 0~2π 1~2 –7~–11 BPSK信号 100~200 无 无 1~2 –7~–11 测试集 LFM信号 100/150/200 20/25/30 0~2π 1~2 –6~–12
(步进–2 dB)BPSK信号 100/150/200 无 无 1~2 –6~–12
(步进–2 dB)表 2 LMS算法与DNN算法在不同信干比下的对消比(LMS算法/DNN算法)(dB)
中心频率(MHz) 信干比(dB) LFM信号带宽 BPSK信号 20 MHz 25 MHz 30 MHz 100 –6 2.51/30.26 2.47/28.80 2.46/27.43 7.20/35.43 –8 4.33/30.95 4.07/30.60 4.13/27.98 5.99/35.78 –10 6.09/31.22 5.64/32.97 5.52/30.81 8.53/38.76 –12 6.83/30.47 8.04/31.60 8.32/28.93 9.68/38.57 150 –6 2.46/30.74 2.48/30.07 2.52/28.24 4.23/33.75 –8 4.47/31.99 4.42/30.12 4.25/29.06 7.73/36.23 –10 5.00/30.52 6.03/31.64 5.85/27.93 8.14/37.18 –12 6.36/28.06 8.27/28.59 7.98/27.60 8.67/39.09 200 –6 2.55/29.54 2.54/27.56 2.10/28.65 5.34/35.07 –8 4.10/32.34 4.54/30.95 4.28/26.01 6.71/35.13 –10 5.94/30.29 6.03/29.10 5.83/26.74 9.28/37.89 –12 7.39/30.10 7.89/28.95 7.40/26.84 8.51/38.15 -
[1] 李永祯, 胡万秋, 陈思伟, 等. 有源转发式干扰的全极化单脉冲雷达抑制方法研究[J]. 电子与信息学报, 2015, 37(2): 276–282. doi: 10.11999/JEIT140146LI Yongzhen, HU Wanqiu, CHEN Siwei, et al. Active repeater jamming suppression using polarimetric monopulse radar[J]. Journal of Electronics &Information Technology, 2015, 37(2): 276–282. doi: 10.11999/JEIT140146 [2] 王峰. 转发式弹载干扰机对抗技术研究[J]. 中国电子科学研究院学报, 2012, 7(4): 423–426. doi: 10.3969/j.issn.1673-5692.2012.04.022WANG Feng. Counter measures for repeater jamming fixed in the missile in Radar’s main-lobe[J]. Journal of China Academy of Electronics and Information Technology, 2012, 7(4): 423–426. doi: 10.3969/j.issn.1673-5692.2012.04.022 [3] REZAZADEH N and SHAFAI L. A compact dual‐band dual‐mode antenna for GPS L1/L2 adaptive interference cancellation[J]. Microwave and Optical Technology Letters, 2020, 62(3): 1230–1236. doi: 10.1002/mop.32114 [4] MOTZ C, PLODER O, PAIREDER T, et al. Enhanced transform-domain LMS based self-interference cancellation in LTE carrier aggregation transceivers[C]. 17th International Conference on Computer Aided Systems Theory, Linz, Austria, 2020: 28–35. [5] 龙戈农, 童宁宁, 李洪兵, 等. 改进的LMS算法及其在雷达干扰对消系统中的应用[J]. 空军工程大学学报(自然科学版), 2010, 11(5): 31–34. doi: 10.3969/j.issn.1009-3516.2010.05.007LONG Genong, TONG Ningning, LI Hongbing, et al. A refrained LMS algorithm and its application in radar jamming cancellation system[J]. Journal of Air Force Engineering University (Natural Science Edition) , 2010, 11(5): 31–34. doi: 10.3969/j.issn.1009-3516.2010.05.007 [6] 姜冰磊, 冯西安. 一种权系数部分更新的变步长自适应多径干扰对消算法[J]. 振动与冲击, 2016, 35(13): 85–89. doi: 10.13465/j.cnki.jvs.2016.13.014JIANG Binglei and FENG Xi’an. A variable step and adaptive multipath interference cancellation algorithm based on partial-update of weight coefficients[J]. Journal of Vibration and Shock, 2016, 35(13): 85–89. doi: 10.13465/j.cnki.jvs.2016.13.014 [7] 刘建成, 全厚德, 赵宏志, 等. 基于迭代变步长LMS的数字域自干扰对消[J]. 电子学报, 2016, 44(7): 1530–1538. doi: 10.3969/j.issn.0372-2112.2016.07.002LIU Jiancheng, QUAN Houde, ZHAO Hongzhi, et al. Digital self-interference cancellation based on iterative variable step-size LMS[J]. Acta Electronica Sinica, 2016, 44(7): 1530–1538. doi: 10.3969/j.issn.0372-2112.2016.07.002 [8] 张兰勇, 王帮民, 刘胜, 等. 一种新的变步长自适应噪声消除算法[J]. 电子学报, 2017, 45(2): 321–327. doi: 10.3969/j.issn.0372-2112.2017.02.009ZHANG Lanyong, WANG Bangmin, LIU Sheng, et al. A novel variable step-size adaptive interference cancellation algorithm[J]. Acta Electronica Sinica, 2017, 45(2): 321–327. doi: 10.3969/j.issn.0372-2112.2017.02.009 [9] XU Tongyang, XU Tianhua, and DARWAZEH I. Deep learning for interference cancellation in non-orthogonal signal based optical communication systems[C]. 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama). , Toyama, Japan, 2018: 241–248. [10] KRISTENSEN A T, BURG A, and BALATSOUKAS-STIMMING A. Advanced machine learning techniques for self-interference cancellation in full-duplex radios[C]. 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, USA, 2019: 1149–1153. [11] MOTADE S N and KULKARNI A V. Channel estimation and data detection using machine learning for MIMO 5G communication systems in fading channel[J]. Technologies, 2018, 6(3): 72. doi: 10.3390/technologies6030072 [12] LI Xiaoyu, YIN Xihang, and YAO Xin. Self-interference cancellation in radar jammer based on deep neural networks[C]. The 2020 4th International Conference on Digital Signal Processing, Chengdu, China, 2020: 234–238. [13] LU Jun, ZHANG Qunfei, SHI Wentao, et al. Variable step-size normalized subband adaptive filtering algorithm for self-interference cancellation[J]. Measurement Science and Technology, 2021, 32(9): 095118. doi: 10.1088/1361-6501/abe9dd [14] 吴飞, 邵士海, 唐友喜. 一种基于多天线波束成形的全双工自干扰抵消算法[J]. 电子学报, 2017, 45(1): 8–15. doi: 10.3969/j.issn.0372-2112.2017.01.002WU Fei, SHAO Shihai, and TANG Youxi. A novel self-interference cancellation algorithm using multi-antenna beamforming in full-duplex system[J]. Acta Electronica Sinica, 2017, 45(1): 8–15. doi: 10.3969/j.issn.0372-2112.2017.01.002 [15] LUO Yongjiang, BI Luhao, and ZHAO Dong. Adaptive digital self-interference cancellation based on fractional order LMS in LFMCW radar[J]. Journal of Systems Engineering and Electronics, 2021, 32(3): 573–583. doi: 10.23919/JSEE.2021.000049 [16] 章坚武, 余皓, 章谦骅. 改进的双曲正切函数的变步长LMS算法[J]. 通信学报, 2020, 41(11): 116–123. doi: 10.11959/j.issn.1000-436x.2020224ZHANG Jianwu, YU Hao, and ZHANG Qianhua. Improved variable step-size LMS algorithm based on hyperbolic tangent function[J]. Journal on Communications, 2020, 41(11): 116–123. doi: 10.11959/j.issn.1000-436x.2020224 [17] 周凯, 李德鑫, 粟毅, 等. 基于雷达发射波形和非匹配滤波联合设计的间歇采样转发干扰抑制方法[J]. 电子与信息学报, 2021, 43(7): 1939–1946. doi: 10.11999/JEIT200299ZHOU Kai, LI Dexin, SU Yi, et al. Joint transmitted waveform and mismatched filter design against interrupted-sampling repeater jamming[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1939–1946. doi: 10.11999/JEIT200299 -





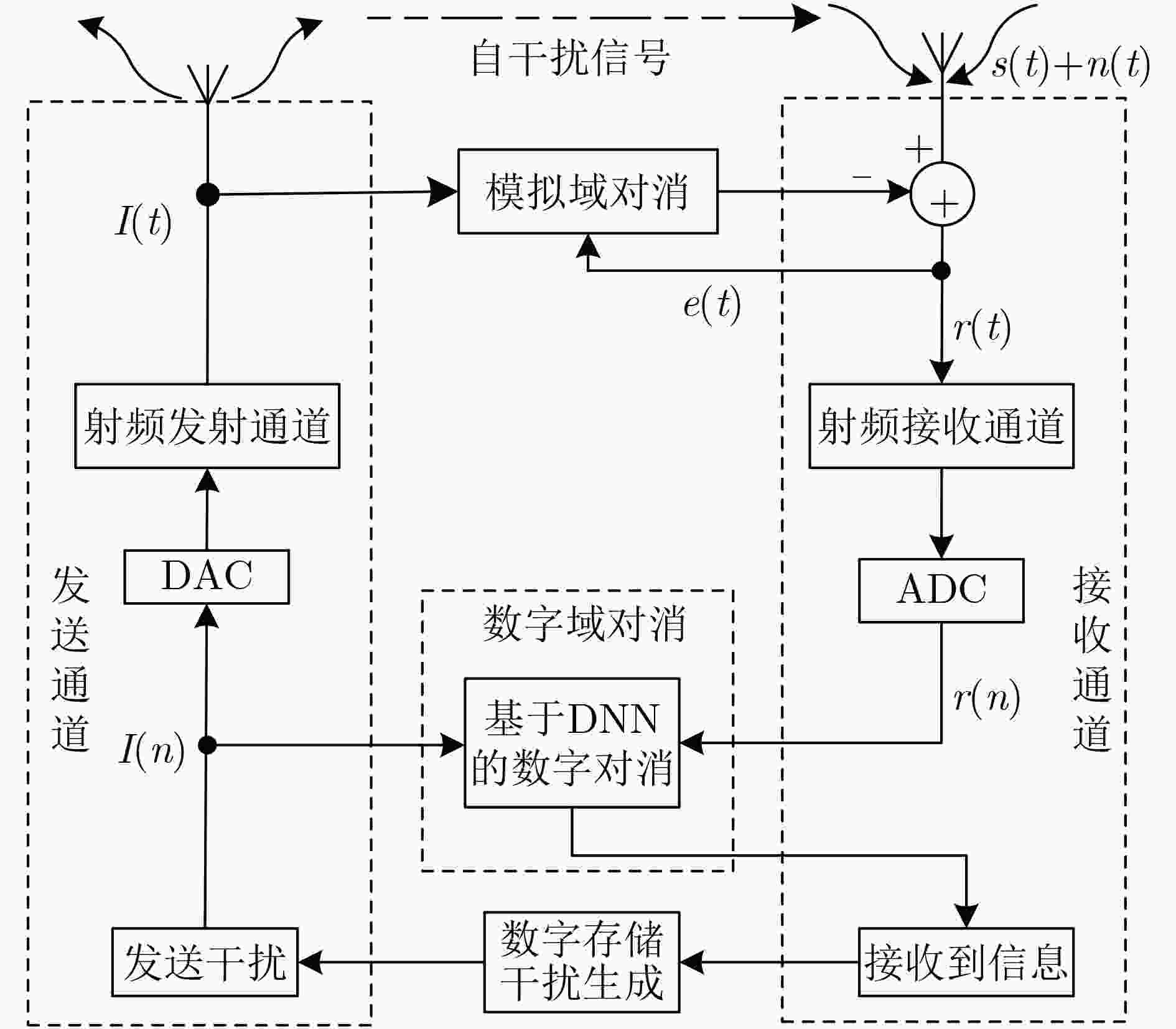
 下载:
下载:
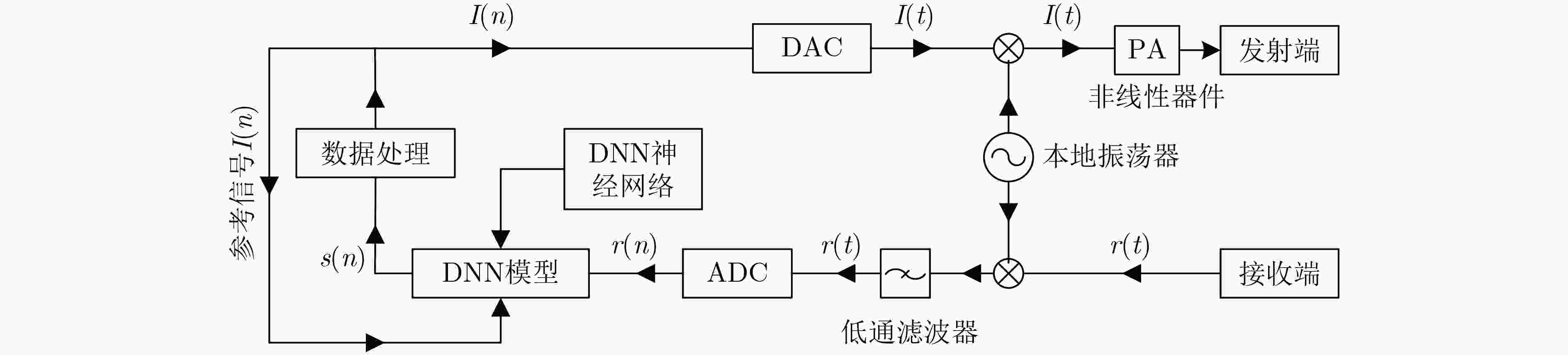
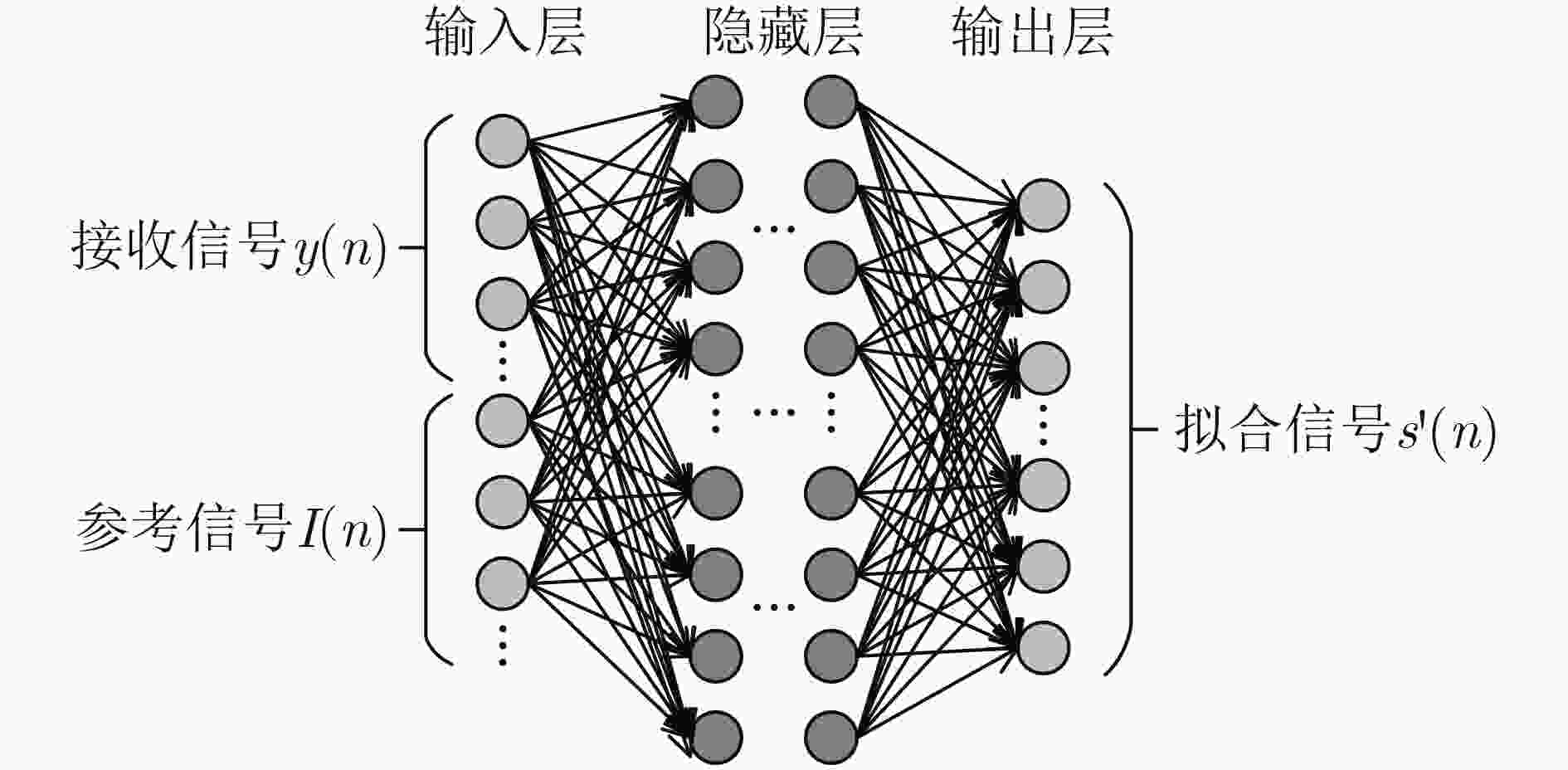

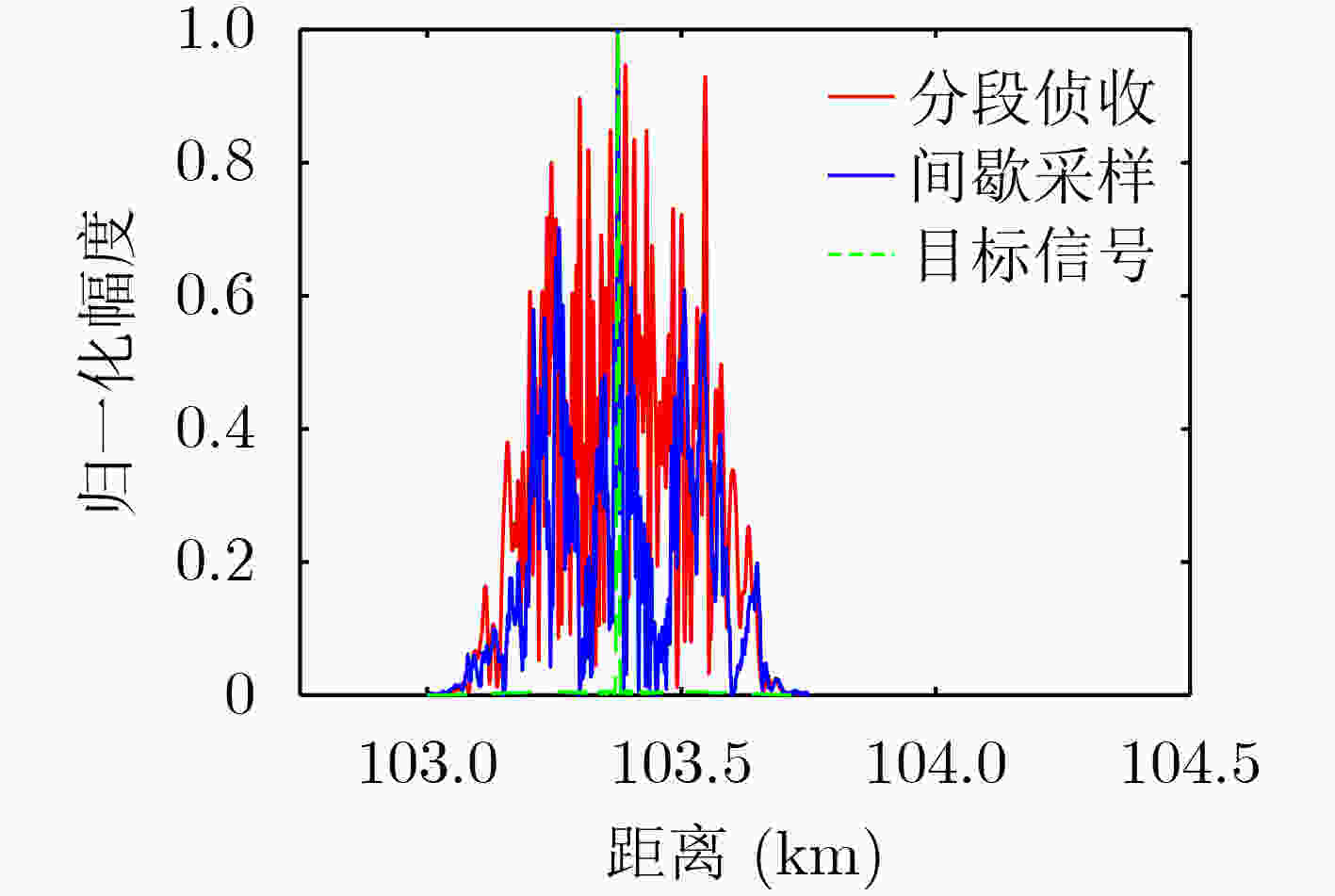



 下载:
下载:
