Research on Symbol Detection of Mixed Signals Based on Sparse AutoEncoder Detector
-
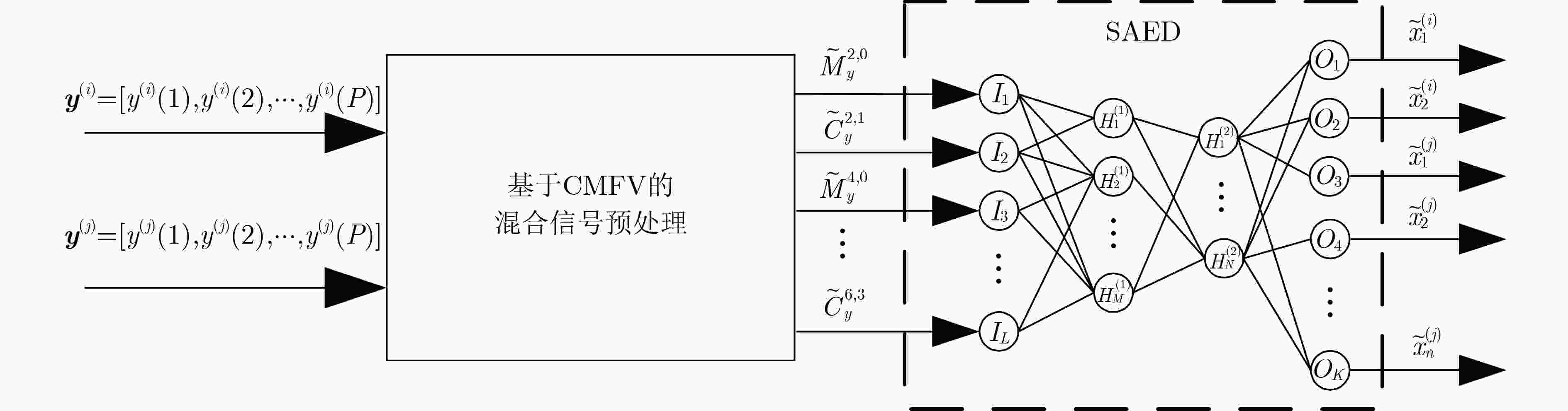
摘要: 基于深度神经网络(DNN)的符号检测器(SD)的结构直接影响检测精度和计算复杂度,然而,已有的工作中并未对DNN符号检测器的结构选择方法开展研究。此外,已知的基于DNN的符号检测器复杂度较高且仅能完成单一调制信号的检测。针对以上问题,该文提出基于误符号率(SER)度量的低复杂度稀疏自编码器符号检测器(SAED)结构选择策略,同时,利用提出的累积量和矩特征向量(CMFV)实现了对混合信号的检测。所设计的符号检测器不依赖信道模型和噪声假设,对不同调制方式的信号具有较好的检测性能。仿真结果表明,该文设计的SAE符号检测器的SER性能接近最大似然(ML)检测理论值,且在频偏、相偏和有限训练样本等非理想条件下具有较强的鲁棒性。Abstract: The architecture of Deep Neural Network (DNN) based detectors can affect the Symbol Detection (SD) accuracy and computational complexity. However, most of the works ignore the architecture selection method when establishing a DNN-based symbol detector. Moreover, the existing DNN detectors use complex architectures and only perform single-type modulated symbols detection. The Symbol Error Rate (SER) based strategy is proposed to design a low complexity Sparse AutoEncoder Detector (SAED) to tackle this problem. Furthermore, a Cumulant and Moment Feature Vector (CMFV)-based method is introduced for mixed symbols detection. Also, the designed symbol detector does not rely on a comprehensive knowledge of channel models and parameters but has the capability to detect various modulation signals. Simulation results show that the SER performance of the SAE symbol detector is close to the values of the Maximum Likelihood (ML) detection approach and provides a stable performance against phase offsets, frequency offsets, and under a limited training dataset.
-
表 1 基于SER度量的SAED结构选择策略
输入: $({\boldsymbol{y} },{\boldsymbol{l} }),\rho ,\xi ,\zeta ,L,\varDelta ,\beta$ 输出:每个隐藏层的候选节点数目$N_i^{{\text{save}}}$ (1) $i \leftarrow 1$ (2) for ${N_i} = 1,2, \cdots ,L$ do (3) 根据式(3)—式(9)计算$\kappa _{{\text{SAED}}}^{{N_i}}$ (4) end for (5) while $\min (\kappa _{ {\text{SAED} } }^{ {N_i} }) - {\kappa _t} > \varDelta$ (6) do ${N_i} = \mathop {\arg }\limits_{ {N_i} \in \left( {1,2, \cdots ,L} \right)} (\min (\kappa _{ {\text{SAED} } }^{ {N_i} }) + \beta )$ (7) $N_i^{{\text{save}}} \leftarrow {N_i}$ (8) $L = \max (N_i^{{\text{save}}})$ (9) $i = i + 1$ (10) for ${N_i} = 1,2, \cdots ,L - 1$ do (11) 根据式(3)—式(9)计算$\kappa _{{\text{SAED}}}^{{N_i}}$ (12) end for (13) end while 表 2 SAED结构和参数配置
结构/参数 节点个数/数值 输入层 8 隐藏层1 7 隐藏层2 3 Softmax层 4,10,12 稀疏系数$(\rho )$ 0.9 稀疏惩罚权重$(\xi )$ 3 权重衰减$(\zeta )$ 0.0001 -
[1] PROAKIS J G. Digital Communications[M]. New York: McGraw-Hill, 2001: 112–180. [2] MENG Fan, CHEN Peng, WU Lenan, et al. Automatic modulation classification: A deep learning enabled approach[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10760–10772. doi: 10.1109/TVT.2018.2868698 [3] 郭晨, 简涛, 徐从安, 等. 基于深度多尺度一维卷积神经网络的雷达舰船目标识别[J]. 电子与信息学报, 2019, 41(6): 1302–1309. doi: 10.11999/JEIT180677GUO Chen, JIAN Tao, XU Congan, et al. Radar HRRP target recognition based on deep multi-scale 1D convolutional neural network[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1302–1309. doi: 10.11999/JEIT180677 [4] 唐伦, 周钰, 谭颀, 等. 基于强化学习的5G网络切片虚拟网络功能迁移算法[J]. 电子与信息学报, 2020, 42(3): 669–677. doi: 10.11999/JEIT190290TANG Lun, ZHOU Yu, TAN Qi, et al. Virtual network function migration algorithm based on reinforcement learning for 5G network slicing[J]. Journal of Electronics &Information Technology, 2020, 42(3): 669–677. doi: 10.11999/JEIT190290 [5] FARSAD N and GOLDSMITH A. Neural network detection of data sequences in communication systems[J]. IEEE Transactions on Signal Processing, 2018, 66(21): 5663–5678. doi: 10.1109/TSP.2018.2868322 [6] LIU Chang, WANG Jie, LIU Xuemeng, et al. Deep CM-CNN for spectrum sensing in cognitive radio[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(10): 2306–2321. doi: 10.1109/JSAC.2019.2933892 [7] O’SHEA T and HOYDIS J. An introduction to deep learning for the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 563–575. doi: 10.1109/TCCN.2017.2758370 [8] ZHANG Min, LIU Zongyan, LI Li, et al. Enhanced efficiency BPSK demodulator based on one-dimensional convolutional neural network[J]. IEEE Access, 2018, 6: 26939–26948. doi: 10.1109/ACCESS.2018.2834144 [9] SAMUEL N, DISKIN T, and WIESEL A. Learning to detect[J]. IEEE Transactions on Signal Processing, 2019, 67(10): 2554–2564. doi: 10.1109/TSP.2019.2899805 [10] GAO Xuanxuan, JIN Shi, WEN Chaokai, et al. ComNet: Combination of deep learning and expert knowledge in OFDM receivers[J]. IEEE Communications Letters, 2018, 22(12): 2627–2630. doi: 10.1109/LCOMM.2018.2877965 [11] GOODFELLOW I, BENGIO Y, and COURVILLE A. Deep Learning[M]. Cambridge: MIT Press, 2016: 306–319. [12] BISHOP C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006: 48–58. [13] SWAMI A and SADLER B M. Hierarchical digital modulation classification using cumulants[J]. IEEE Transactions on Communications, 2000, 48(3): 416–429. doi: 10.1109/26.837045 [14] NIKIAS C L and MENDEL J M. Signal processing with higher-order spectra[J]. IEEE Signal Processing Magazine, 1993, 10(3): 10–37. doi: 10.1109/79.221324 [15] YE Hao, LI G Y, and JUANG B H. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114–117. doi: 10.1109/LWC.2017.2757490 [16] DÖRNER S, CAMMERER S, HOYDIS J, et al. Deep learning based communication over the air[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 132–143. doi: 10.1109/JSTSP.2017.2784180 -





 下载:
下载:



 下载:
下载:
