Research on Timed-Release Encryption System Based on Multiple Time Servers
-
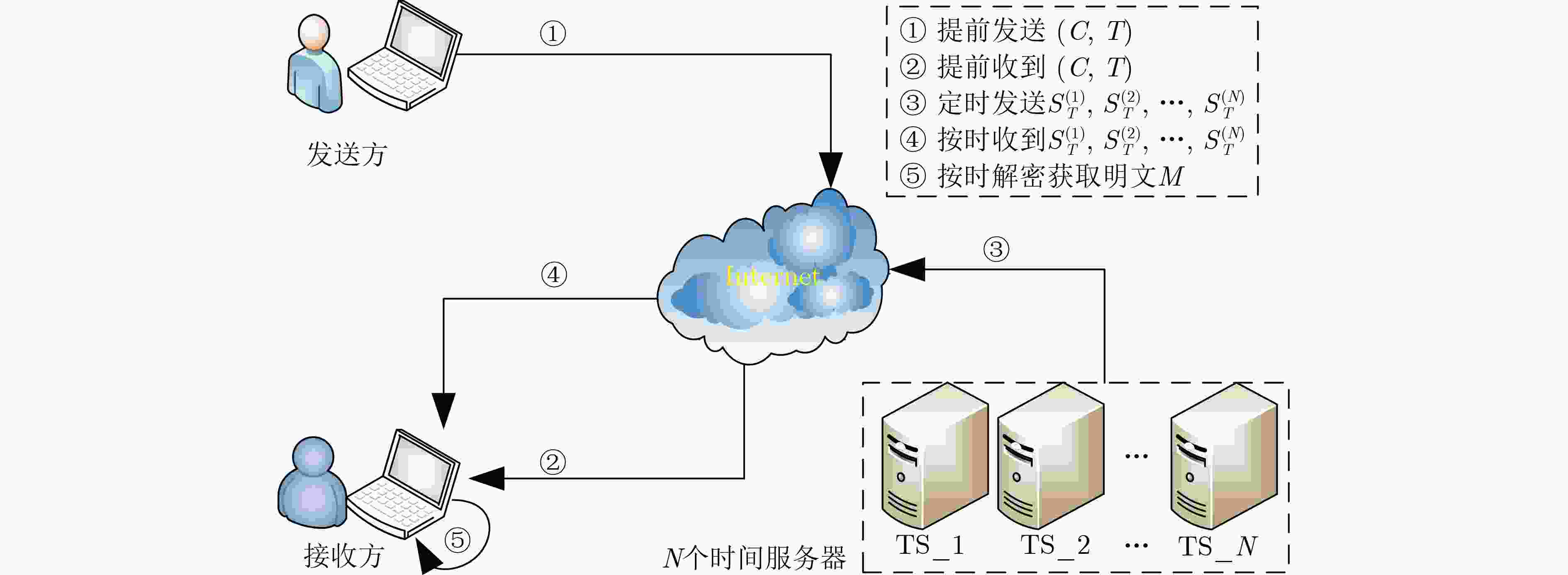
摘要: 时控性加密(TRE)是一种被称为“向未来发送消息”的密码原语,接收方在未来指定时间之前无法解密密文。目前,大部分TRE方案采用非交互式单时间服务器方法,系统用户能够正常解密,依赖于单一时间服务器在预定解密时间计算并广播的时间陷门。如果单一的时间服务器遭受攻击,或被腐败,则容易直接威胁TRE的安全应用。因此,需要将1个时间服务器“分散”成多个。但已有多时间服务器TRE方案既没有给出安全性分析,也没有给出严格的安全性证明。为此,该文给出一种随机预言机模型下基于双线性迪菲·赫尔曼(BDH)问题的多时间服务器的TRE模型MTSTRE,构造出一种可证明安全的具体和通用方案,并严格证明所提具体方案在自适应选择明文攻击下是安全的。效率分析表明,与已有最有效的多时间服务器TRE解决方案相比,所提具体方案的计算效率也略有提高。Abstract: Timed-Release Encryption (TRE) is a cryptographic primitive called "sending messages into the future", the receiver can not decrypt the ciphertext until a designed time in the future. Currently, most TRE schemes use a non-interactive single time server approach, where the system user is able to decrypt properly, relying on a time trapdoor calculated and broadcast by a time server at the designed decryption time. If the single time server is attacked or corrupted, it is prone to directly threaten the TRE security application. Therefore, a single time server needs to be “distributed” into multiple ones. However, existing multiple time servers TRE schemes do not provide neither the security analysis nor the strict formal security proofs. To deal with this problem, a new Multiple Time Servers TRE (MTSTRE) scheme based on Bilinear Diffie-Hellman (BDH) problem in the random oracle model is proposed, a concrete scheme with provable security and a general scheme is proposed, and then it is strictly proved that the concrete scheme is security under adaptive chosen-plaintext attack. Efficiency analysis shows that compared with the most effective existing multiple time servers TRE scheme, the calculation efficiency of the concrete scheme is slightly improved.
-
表 1 其他基本运算相对于PMec运算的相对耗时统计表
基本运算操作 标识符号 相对耗时(PMT) 双线性对运算 BP 3.7870 G1群上的点乘运算 PMec 1 G1群上的点加运算 PAec 0.0074 G2群上的幂运算 Expdl 0.3409 G2群上的乘运算 Muldl 0.0026 $ \mathbb{Z}_q^* $上的模逆运算 Inv 0.0029 $ {H_1} $函数:${\{ 0,1\} ^*} \to {G_1}$ H1 0.3214 $ {H_2} $函数:${G_2} \to {\{ 0,1\} ^{ { {\log}_{2} }q} }$ H2 0.0784 表 2 多时间服务器TRE方案相对耗时表
表 3 密封投标应用场景相对耗时统计表(PMT)
阶段 Enc TS-Rel Dec 总计 相对耗时 31.304 1.3214 19.697 52.3224 -
[1] RIVEST R L, SHAMIR A, and WAGNER D A. Time-lock puzzles and timed-release crypto[R]. 1996. [2] 王通, 何宇帆, 李磊. 基于不可区分混淆的定时释放密码方案[J]. 计算机应用研究, 2017, 34(9): 2795–2798. doi: 10.3969/j.issn.1001-3695.2017.09.051WANG Tong, HE Yufan, and LI Lei. New timed-release encryption based on indistinguishability obfuscation[J]. Application Research of Computers, 2017, 34(9): 2795–2798. doi: 10.3969/j.issn.1001-3695.2017.09.051 [3] UNRUH D. Revocable quantum timed-release encryption[J]. Journal of the ACM, 2015, 62(6): 49. doi: 10.1145/2817206 [4] CHAE S W, KIM J I, and PARK Y. Practical time-release blockchain[J]. Electronics, 2020, 9(4): 672. doi: 10.3390/electronics9040672 [5] KAVITHA V, GEETHA D, KARUNKUZHALI D, et al. A completely distributed blockchain period authentication framework[J]. Journal of Physics:Conference Series, 2021, 1964: 042047. doi: 10.1088/1742-6596/1964/4/042047 [6] MANGIPUDI E V, LU Donghang, PSOMAS A, et al. Collusion-deterrent threshold information escrow[R]. 2021. [7] BITANSKY N, GOLDWASSER S, JAIN A, et al. Time-lock puzzles from randomized encodings[C]. 2016 ACM Conference on Innovations in Theoretical Computer Science, Cambridge, USA, 2016: 345–356. [8] FAN C I, CHEN Juncheng, HUANG Shiyuan, et al. Provably secure timed-release proxy conditional reencryption[J]. IEEE Systems Journal, 2017, 11(4): 2291–2302. doi: 10.1109/JSYST.2014.2385778 [9] CHAN A C F and BLAKE I F. Scalable, server-passive, user-anonymous timed release cryptography[C]. The 25th IEEE International Conference on Distributed Computing Systems, Columbus, USA, 2005: 504–513. [10] HRISTU-VARSAKELIS D, CHALKIAS K, and STEPHANIDES G. A versatile secure protocol for anonymous timed-release encryption[J]. Journal of Information Assurance and Security, 2008, 3(5): 80–89. [11] WATANABE Y and SHIKATA J. Timed-release computational secret sharing and threshold encryption[J]. Designs, Codes and Cryptography, 2018, 86(1): 17–54. doi: 10.1007/s10623-016-0324-2 [12] HONG Jianan, XUE Kaiping, XUE Yingjie, et al. TAFC: Time and attribute factors combined access control for time-sensitive data in public cloud[J]. IEEE Transactions on Services Computing, 2020, 13(1): 158–171. doi: 10.1109/TSC.2017.2682090 [13] ISHIZAKA M and KIYOMOTO S. Time-specific encryption with constant-size secret-keys secure under standard assumption[EB/OL].https://eprint.iacr.org/2020/595.pdf, 2020. [14] LEE K. Self-updatable encryption with short public parameters and its extensions[J]. Designs, Codes and Cryptography, 2016, 79(1): 121–161. doi: 10.1007/s10623-015-0039-9 [15] WANG Xu’an, SANGAIAH A K, NEDJAH N, et al. On the security of a CCA-secure timed-release conditional proxy broadcast re-encryption scheme[M]. XHAFA F, LEU F Y, FICCO M, et al. Advances on P2P, Parallel, Grid, Cloud and Internet Computing. Cham: Springer, 2018: 192–198. [16] 袁科, 王亚慧, 汤茜, 等. 一种支持任意指定时间解密的时间控制加密系统及方法[P]. 中国专利, 111556009A, 2020.YUAN Ke, WANG Yahui, TANG Qian, et al. Time control encryption system and method supporting decryption at any specified time[P]. China Patent, 111556009A, 2020. [17] MERKLE R C. Secure communications over insecure channels[J]. Communications of the ACM, 1978, 21(4): 294–299. doi: 10.1145/359460.359473 [18] GOWDA B K and SUMATHI R. Hierarchy attribute-based encryption with timing enabled privacy preserving keyword search mechanism for e-health clouds[C]. The 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology, Bangalore, India, 2017: 425–429. [19] MONT M C, HARRISON K, and SADLER M. The HP time vault service: Innovating the way confidential information is disclosed, at the right time[R]. HPL-2002-243, 2002. [20] YUAN Ke, WANG Yahui, ZENG Yingming, et al. Provably secure security-enhanced timed-release encryption in the random oracle model[J]. Security and Communication Networks, 2021, 2021: 5593363. doi: 10.1155/2021/5593363 -





 下载:
下载:


 下载:
下载:
