Wireless Communications Interference Avoidance Based on Fast Reinforcement Learning
-
摘要: 针对无线通信环境中存在未知且动态变化的干扰，该文联合考虑通信信道接入和发射功率控制提出了基于快速强化学习的未知干扰规避策略，以确保通信收发端的可靠通信。将干扰规避问题建模为马尔可夫决策过程，其优化目标为在保证通信质量的前提下同时降低系统发射功率和减少信道切换次数。随后，提出一种赢或学习快速策略爬山(WoLF-PHC)学习方法的干扰规避方案，从而实现快速规避干扰的目的。仿真结果表明，在不同干扰模式下，所提WoLF-PHC算法的抗干扰性能、收敛速度均优于传统的随机选择方法和Q学习算法。
-
关键词:
- 干扰规避 /
- 赢或学习快速策略爬山 /
- Q学习 /
- 马尔可夫决策
Abstract: In this article, the unknown and dynamic interference in the wireless communication environment is studied. Jointly considering communication channel access and transmit power control, a fast reinforcement learning strategy is proposed to ensure reliable communication at the transceivers. The interference avoidance problem is firstly modeled as a Markov decision process to lower the transmission power of the system and reduce the number of channel switching while ensuring the communication quality. Subsequently, a Win or Learn Fast Policy Hill-Climbing (WoLF-PHC) learning method is proposed to avoid rapidly interference. Simulation results show that the anti-interference performance and convergence speed of the proposed WoLF-PHC algorithm are superior to the traditional random selection method and Q learning algorithm under different interference situations. -
1. 引言
无线通信信道的开放性使其更容易受到未知干扰攻击，对正常通信构成威胁，因此抗干扰技术得到了广泛的研究[1,2]。抗干扰技术主要是通过频谱感知方式[3]检测干扰信息，并根据自身通信状态进行干扰规避和对抗的过程，从而改善通信效率。干扰规避常用技术主要包括跳频 (Frequency Hopping, FH)、传输速率自适应 (Rate Adaptive, RA)、功率控制等。如果干扰规律已知且恒定，可以使用监督学习进行训练，得到特定的策略进行规避。但是一般无线环境中干扰规律未知且动态变化，预先制定好的规避策略难以适应环境变化。当干扰变化时原策略可能失效，无法采用监督学习制定策略来优化通信性能，需要探索更加有效的干扰规避算法。
在时域和频域都动态变化的通信环境中，业界通常利用强化学习 (Reinforcement Learning, RL) 与环境进行交互获得学习经验来优化干扰规避策略[4]，从而达到规避干扰的目的。近年来，许多学者将动态频谱接入 (Dynamic Spectrum Access, DSA) 和Q学习进行结合，提出了多种有效的智能抗干扰方法。文献[5,6]将信道选择问题建模为马尔可夫决策过程 (Markov Decision Process, MDP)，提出了一种智能选择最优信道的实时强化学习算法(即Q学习)，从而选择条件较好的信道进行数据传输来主动避免信道拥塞。在文献[7]中，应用极小极大-Q原理来确定用于传输数据信道的数目，并确定了如何在不同信道之间进行信道切换的方案以规避干扰。文献[8]在多信道动态抗干扰博弈中，基于强化Q学习技术提出了一种最优的信道接入策略。此外，在认知无线网络(Cognitive wireless Network, CRN)场景中，文献[9]提出的基于策略同步Q学习的信道分配策略主动避免了网络中的信道拥塞问题。然而，以上算法均只采用信道切换进行躲避干扰，显然频繁的信道切换会增大系统开销，并不能带来整体性能的提升，因此需要考虑其他方式来进行躲避干扰，完成正常通信。
随着通信设备的更新换代，越来越多的通信设备开始具有切换通信频率和调节发射功率的能力[10]。文献[11]首次研究了多用户场景下同时进行信道选择和功率分配决策的协作抗干扰问题，并将该问题建模为一个多主一从的Stackelberg博弈过程。文献[12,13]提出的零和博弈研究了跳频和传输速率控制，通过联合优化跳频和传输速率自适应技术来避免干扰。无线通信系统中的发送机通过改变其信道、调整其速率或同时改变这两种方式来避开干扰，以提高系统的平均吞吐量，但该文献仅对反应式扫频干扰这一种干扰模式做出了分析，并不适用于多种干扰环境。而文献[14]则将上述决策问题描述为一个马尔可夫决策过程，提出了一种基于深度强化学习 (Deep Reinforcement Learning, DRL)的抗干扰算法，该算法可以同时对通信频率和功率进行决策，但是该算法并没有考虑信道切换的代价，不能从多方面说明算法的优势。基于Q学习的2维抗干扰移动通信方案[15]为每个状态策略保留Q函数，用于选择发射功率和接入信道，但是状态空间维度过大会造成Q学习的学习速度降低，难以适应动态变化的无线通信环境。
针对动态变化的干扰环境，干扰规避策略不仅需要考虑通信信道的接入和发射功率控制，还应该考虑算法收敛速度以快速适应环境变化。考虑这一联合优化目标，本文将动态变化环境中的干扰规避问题建模为一个马尔可夫决策过程，提出了一种赢或学习快速策略爬山 (Win or Learn Fast Policy Hill-Climbing, WoLF-PHC)的干扰规避方法，本方法使用“赢或快学习”准则以及可变的学习率，从而更快地实现最优的干扰规避策略。本文主要的研究工作如下：
(1) 首先基于实际无线通信环境，建立2维时频域的经典干扰模型，比如扫频干扰、随机干扰、跟随式干扰、贪婪随机策略干扰，用于后续仿真验证。
(2) 然后将干扰环境下的接入信道和发射功率控制问题建模为一个马尔可夫决策过程，分别给出状态、动作、转移概率和奖励4个元素，并将其定义为一个4元组
$(S,A,p,R)$ 。(3) 介绍传统Q学习算法，接着提出一种基于WoLF-PHC学习的快速干扰规避算法。
(4) 将所提的WoLF-PHC算法与传统Q学习和随机策略进行仿真对比，验证了所提WoLF-PHC算法性能最佳。
2. 系统模型及问题描述
2.1 干扰模型
为了模拟无线通信环境中的未知干扰，干扰机在每个时隙随机选择干扰信道并发送特定干扰功率的干扰信号，以恶化或中断正在进行的通信链路。本文考虑4种干扰模型[15]场景，分别为扫频干扰、贪婪随机策略干扰、跟随式干扰、随机干扰。具体定义如下：
(1) 扫频干扰：每个时隙干扰m个信道，总信道数M为m的整数倍，扫频周期即为
$T = {M}/{m}$ 。例如，在第1个扫描周期先产生一个随机序列$ \left[ {3,5,1,4,2,6} \right] $ ，即第1个时隙干扰信道$ \left[ {{f_3},{f_5}} \right] $ ，第2个时隙干扰信道$ \left[ {{f_1},{f_4}} \right] $ ，第3个时隙干扰信道$ \left[ {{f_2},{f_6}} \right] $ 。当一个扫频周期结束之后，继续重复上一个周期的干扰策略。(2) 贪婪随机策略干扰：每个时隙随机选择干扰信道，使用
${P_0} = 1- \varepsilon $ 的概率干扰相同信道，${P_1} = \varepsilon $ 的概率随机干扰新信道。假设每个时隙生成一个$ \left( {0,1} \right) $ 的随机数，如果这个随机数小于$\varepsilon $ ，则随机干扰一个新信道，如果这个随机数大于$\varepsilon $ ，那么继续干扰原信道。(3) 跟随式干扰：根据正在进行通信的信道来选择干扰策略。即干扰上一时隙通信所采用的信道，上一时隙通信采用哪个信道，当前时隙就干扰哪个信道。
(4) 随机干扰：每个时隙随机选择信道和干扰功率进行干扰。
2.2 问题分析与建模
如图1所示，考虑无线通信环境中，存在发送机、干扰机、接收机。设信道增益为1，发送信号为x(t)，噪声为n(t)，干扰信号为z(t)，那么接收信号y(t)为
$$ y(t) = x(t) + z(t) + n(t) $$ (1) 假设该系统中发送机的发射功率集合为
${P_{\text{U}}} = \{ {p_{{\rm{u}}1}},{p_{{\rm{u}}2}},\cdots,{p_{{\rm{u}}i,}}\cdots,{p_{{\rm{u}}L}}\}$ ，${p_{{\rm{u}}i}}$ 表示可供选择的发射功率大小，共有L种发射功率。第$k$ 个时隙所使用的发射功率记为$ p_{\text{u}}^k $ ，$p_{\text{u}}^k \in {P_{\text{U}}}$ 。干扰功率集合设为${P_{\text{J}}} = {\text{\{ }}{p_{{\rm{j}}1}},{p_{{\rm{j}}2}},\cdots,{p_{{\rm{j}}i}},\cdots,{p_{{\rm{j}}W}}{\text{\} }}$ ，${p_{{\rm{j}}i}}$ 表示可供选择的干扰功率大小，共有W种发射功率。第$k$ 个时隙干扰功率记为$p_{\text{j}}^k$ ，$p_{\text{j}}^k \in {P_{\text{J}}}$ ，噪声功率为${\sigma ^2}$ 。利用频谱感知算法[3]，我们可以获得未知环境下的干扰信息(即干扰所占信道和干扰功率)。基于这一干扰信息，发送机需要选择合适的信道和发射功率使接收信号达到一定的信干噪比，完成正常解调达到正常通信的目的。发送机应尽量减少信道的切换和发射功率，以达到较少开销的目的。这里引入信道切换代价和功率来衡量系统开销。所谓信道切换代价，即为后一时隙与前一时隙选择的通信信道不同时，进行信道切换所带来的代价；而功率代价，即为所使用的发射功率越大，成本越大。因此，在未知且动态变化的干扰环境中，发送机应需要尽量减少信道切换和发射功率的代价，同时还要规避干扰，从而完成正常通信。本文将未知环境下发送机选择信道和功率控制过程建模为一个马尔可夫决策过程 (Markov Decision Process, MDP)[6]。MDP为寻找最优策略提供了数学模型，在描述MDP时，通常采用状态、动作、转移概率和奖励这4个元素，并将其定义为一个4元组
$(S,A,p,R)$ 。其中，状态空间$S$ 和动作空间$A$ 是离散的，由于本文的下一状态由当前动作确定，所以状态转移概率为确定值，记为$ p:S \times S \times A \to [0,1] $ ，表示给定当前状态${s^k} \in S$ 下选择动作${a^k} \in A$ 转移到下一状态${s^{k + 1}} \in S$ 的概率。本文的MDP模型具体如下：(1) 状态：定义第
$ k $ 个时隙的状态为${s^k} = (f_{\text{u}}^k,f_{\text{j}}^k)$ ，其中${f}_{\text{u}}^{k},{f}_{\text{j}}^{k}\in \{1,2,\cdots ,M\}$ ，前者表示当前时隙选择的通信信道，后者表示当前时隙干扰所占用的信道，设状态空间为$S$ 。(2) 动作：定义在第k个时隙用户采取的动作为
${a^k} = ({f^{k + 1}_{\text{u}}},{p^{k + 1}_{\text{u}}})$ ，其中${f^{k + 1}_{\text{u}}} \in \{ 1,2, \cdots ,M\}$ ,${p^{k + 1}_{\text{u}}} \in {P_{\text{U}}}$ 。${f^{k + 1}_{\text{u}}}$ 为第$ k + 1 $ 个时隙用户选择的通信信道，${p^{k + 1}_{\text{u}}}$ 为第$ k + 1 $ 个时隙用户采用的发射功率，动作空间大小为$ M \times L $ ，记为$A$ 。(3) 奖励函数：当用户在
$ {s^k} $ 状态执行动作$ {a^k} $ 时，会获得相应的奖励值$ {R^k} $ 。这里定义第k个时隙的信干噪比 (Signal to Interference plus Noise Ratio, SINR)为$$ {\text{SIN}}{{\text{R}}^k} = \frac{{p_{\text{u}}^{k + 1}}}{{p_{\text{j}}^{k + 1}\varphi (f_{\text{u}}^{k + 1},f_{\text{j}}^{k + 1}) + {\sigma ^2}}} $$ (2) 其中，
$\varphi ({f}_{\text{u}}^{k+1},{f}_{\text{j}}^{k+1})\text{=}\left\{\begin{array}{l}1,\text{ }{f}_{\text{u}}^{k+1}\in {f}_{\text{j}}^{k+1}\\ 0,其他\end{array} \right.$ ，即如果通信信道受到干扰，则$\varphi (\cdot)$ 为1；否则为0。当${\text{SINR}} \ge {T_{\text{h}}}$ 时，表示接收机能正常解调接收信号完成正常通信；否则表示当前通信失败，其中${T_{\text{h}}}$ 表示根据实际应用所选择的最小SINR门限值。设信道切换代价为${C_{\text{f}}}$ ，功率代价为${C_{\text{P}}}\times \dfrac{{p_{\text{u}}^{k + 1}}}{{{p_{\max }}}}$ ，${p_{\max }}$ 表示最大发射功率，${C_{\text{P}}}$ 表示最大功率传输代价。奖励值$ {R^k} $ 由是否正常通信、功率代价和信道切换代价共同决定，可定义为[12]$$ \begin{split} &{R^k}{\text{ = }}\\ &\left\{ \begin{gathered} 1 - {C_{\text{P}}} \times \frac{{p_{\text{u}}^{k + 1}}}{{{p_{\max }}}} - {C_{\text{f}}} \times {K}(f_{\text{u}}^k,f_{\text{u}}^{k + 1}),{\text{ SINR}} \ge {T_{\text{h}}} \\ - 1 - {C_{\text{P}}} \times \frac{{p_{\text{u}}^{k + 1}}}{{{p_{\max }}}} - {C_{\text{f}}} \times {K}(f_{\text{u}}^k,f_{\text{u}}^{k + 1}),{\text{ SINR}} < {T_{\text{h}}}{\kern 1pt} \\ \end{gathered} \right. \end{split} $$ (3) 其中，
$ K(f_{\text{u}}^k,f_{\text{u}}^{k + 1}){\text{ = }}\left\{ \begin{gathered} 1,{\text{ }}f_{\text{u}}^k \ne f_{\text{u}}^{k + 1} \\ 0,{\text{ }}f_{\text{u}}^k = f_{\text{u}}^{k + 1} \\ \end{gathered} \right. $ ，即前一时隙与后一时隙采用不同通信信道时进行了信道切换，将产生信道切换代价。当${\text{SINR}} \ge {T_{\text{h}}}$ 时，表示正常通信，记为1，并减去相应的信道切换代价和功率代价可得奖励值。在学习过程中，用户不断与环境交互，探索干扰的变化规律，从而获得最优的传输策略。本文的系统目标是优化用户的传输策略
$\pi $ ，使系统的长期累积收益最大化，因此系统优化问题可以建模为$$ \mathop {\max }\limits_\pi E\left[ {\sum\limits_{i = 1}^\infty {{\gamma ^{i - 1}}} {R^{k + i}}} \right] $$ (4) 其中，γ (0<γ≤1)为折扣因子，表示未来收益对当前收益的重要程度。
由于问题式(4)被建模为马尔可夫决策问题，可以采用Q学习方法与环境进行实时交互，根据选取动作得到下一时隙的反馈奖励值，并不断更新2维Q矩阵来实现抗干扰策略的优化。下面将介绍传统Q学习算法，并对该算法的现有缺陷进行分析，进而提出一种基于WoLF-PHC的快速强化学习算法。所提算法在未知干扰模型且干扰动态变化的情况下，不仅能保持Q学习的性能，而且能快速学习干扰变化规律并获得最优规避策略，在随机干扰的情况下也能保证收敛。
3. 基于快速强化学习的干扰规避算法
3.1 传统Q学习算法
采用Q学习的方法来解决MDP问题的主要思想是将状态和动作构建成一张2维Q表来存储Q值，然后根据Q值来选取能够获得最大收益的动作。Q表中的元素即
$ Q(s,a) $ ，表示在某一时隙的s状态下(s∈S)，采取动作a(a∈A)后预计能够得到的累计奖励值。在第k个时隙的状态s下采取动作a，更新的Q函数为[6,12]$$ \begin{split} {Q^{k + 1}}\left( {{s^k},{a^k}} \right) =& (1 - \alpha ){Q^k}\left( {{s^k},{a^k}} \right) \\ &+ \alpha \left( {{R^k} + \gamma {{\max }_a}{Q^k}\left( {{s^{k + 1}},a} \right)} \right) \end{split} $$ (5) 其中，
${s^k}$ ,${a^k}$ 分别表示当前的动作和状态，$\alpha \in (0,1]$ 表示学习率，$\gamma \in (0,1]$ 表示折扣因子，${R^k}$ 代表在$ {s^k} $ 状态执行动作${a^k}$ 时获得的奖励值。${Q^k}\left( {{s^k},{a^k}} \right)$ 为当前的Q值，${Q^{k + 1}}\left( {{s^k},{a^k}} \right)$ 则表示更新后的Q值。${\max _a}{Q^k}\left( {{s^{k + 1}},a} \right)$ 表示下一个状态所有Q值中的最大值。在基于Q学习的选择策略中，如果用户总是选择Q值对应最大的动作，算法容易陷入局部最优，因此可以采用贪婪策略选择动作。在贪婪选择动作的过程中，产生一个
$[0,1]$ 的随机数，如果该数小于$\varepsilon $ ，则随机采取一个动作，否则选择Q值最大对应的动作。贪婪策略[16]定义为$$ \pi (s,a) = \left\{ {\begin{array}{*{20}{l}} \mathop {\arg \max }\limits_a Q(s,a),&{p_{\text{r}}} < \varepsilon \\ {a_{{\text{ran}}}}{\text{, }}&{p_{\text{r}}} \ge \varepsilon \end{array}} \right. $$ (6) 基于Q学习的功率和信道选择策略具体步骤如表1所示。
表 1 基于Q学习的功率和信道选择策略初始化：设k=0，确定初始状态$ {s^k} = (f_{\text{u}}^k,f_{\text{j}}^k) $，随机选择当前时隙通信信道$f_{\text{u}}^k$，并且进行频谱感知获取当前时隙的干扰信道$f_{\text{j}}^k$以及干扰功
率$ {p_{\text{j}}}^k $；初始化Q表为全0矩阵；设置学习率$\alpha $，折扣因子$\gamma $；学习过程：当$ k < K $时， (1) 利用贪婪策略选取动作$ {a^k} = ({f_{\text{u}}}^{k + 1},{p_{\text{u}}}^{k + 1}) $，然后再根据频谱感知结果，和选取的动作更新下一时隙的状态${s^{k{\text{ + }}1}} = (f_{\text{u}}^{k{\text{ + }}1},f_{\text{j}}^{k{\text{ + }}1})$，
计算出${\text{SIN}}{{\text{R}}^k}$和下一时隙反馈的奖励值$ {R^k} $；(2) 根据式(5)，更新Q表，$ k = k + 1 $。 Q学习采用恒定的学习率，收敛速度较慢。根据后面仿真结果图2(d)可知，针对随机策略的干扰该算法不一定达到收敛。在实际无线通信场景中，很难预知干扰的动态变化情况。可见，传统Q学习算法并不适用于所有环境。为此，本文提出了一种新的WoLF-PHC算法，其采用可变的学习率使用户加快学习，并且根据赢或快学习(Win or Learn Fast, WoLF)准则保证了算法的收敛性。
3.2 WoLF-PHC算法
赢或学习快速策略爬山(WoLF-PHC)[17]是将“赢或快学习” (WoLF)规则与“策略爬山法” (Policy Hill-Climbing, PHC)相结合的一种学习算法。其中PHC算法是Q学习的简单扩展，通过学习率
$ \delta \in (0,1) $ 逐步增大选择最大行为值(即Q值)的概率来改进策略。当$\delta {\text{ = }}1$ 时，该算法等效于Q学习算法。该算法中，Q函数的更新规则与Q学习算法中的更新规则相同，即式(5)所示。然而，面对随机策略干扰，PHC算法依然无法收敛。因此，文献[16]进一步引入了WoLF算法以确保算法收敛。当用户当前“赢”时，缓慢调整学习速率，当用户“输”时，加快学习速率，这样使得PHC算法能够收敛到纳什均衡。当前策略$\pi (s,a)$ 和平均策略$\bar \pi (s,a)$ 之间的差异可以作为判断算法输或赢的标准。为了计算平均策略，引入$C(s)$ 表示当前状态$s$ 出现的次数，平均策略的规则为$$ \begin{split} \bar \pi \left( {s,a} \right) \leftarrow& \bar \pi \left( {s,a} \right) \\ & + \frac{1}{{C(s)}}\left( {\pi \left( {s,a} \right) - \bar \pi \left( {s,a} \right)} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a \in A \end{split} $$ (7) 当前策略
$\pi (s,a)$ 的初始值为${1}/{{|A|}}$ ，$|A|$ 为动作空间的长度。如果选择最大Q值的动作，则当前策略增加一个值；而选择其他动作则减去一个值。当前策略的更新规则可表示为$$ \pi \left( {s,a} \right) \leftarrow \pi \left( {s,a} \right) + \left\{ \begin{gathered} \varDelta ,a = \arg {\max _a}Q\left( {s,a} \right) \\ \frac{{ - \varDelta }}{{\left| A \right| - 1}} \\ \end{gathered} \right. $$ (8) 其中
$$ \begin{split} &\varDelta=\\ &\left\{\begin{array}{l} -\mathrm{min}\left(\pi \left(s,a\right),\dfrac{\delta }{\left|A\right|-1}\right), \text{}a\ne \mathrm{arg}{\mathrm{max}}_{a{'}\in A}Q\left(s,a {'}\right)\text{ }\\ {\displaystyle \sum _{a{'}\ne a}\mathrm{min}}\left(\pi \left(s,a{'}\right),\dfrac{\delta }{\left|A\right|-1}\right),其他\end{array} \right. \end{split} $$ $$ $$ (9) 其中，
$\delta $ 取决于当前策略平均奖励值$\displaystyle\sum\limits a \pi (s,a) Q(s,a)$ 和平均策略平均奖励值$\displaystyle\sum\limits a {\bar \pi } (s,a)Q(s,a)$ ，当前者大于后者时，认为当前代理(Agent)是“赢”的，则采用小的学习速率${\delta _{\text{w}}}$ 缓慢学习；否则采用大的学习速率${\delta _{\text{l}}}$ 快速学习，这里${\delta _{\text{l}}} > {\delta _{\text{w}}}$ 。WoLF-PHC算法引入两种学习速率，不但能加快学习速度还能使用户收敛到最优策略。基于WoLF-PHC学习的功率和信道策略具体步骤如表2所示。
表 2 基于WoLF-PHC学习的功率和信道选择策略初始化：折扣因子$\gamma $，学习率$\alpha $，学习速率${\delta _{\text{l}}}$, ${\delta _{\text{w}}}$；Q表为全0矩阵，$\pi \left( {s,a} \right){\text{ = } }{1}/{ { {\text{|} }A{\text{|} } } }$, $C({{s} }) = 0$； 学习过程：当$ k < K $时， (1) 根据当前策略$\pi (s,a)$和当前状态$s$选择动作$a$； (2) 获取下一时隙的状态$s$并计算$ R $，然后根据式(5)，更新Q表； (3) 更新$C({{s} }) \leftarrow C(s) + 1$，再根据式(8)和式(7)更新$\pi (s,a)$和$\bar \pi (s,a)$ (4) $ k{\text{ }} = {\text{ }}k + 1 $。 4. 仿真分析
本节主要基于所提WoLF-PHC算法、Q学习算法以及随机策略进行信道和发射功率的选择，并对这3种算法进行仿真分析对比。其中，随机策略是根据上一时隙的感知结果，下一时隙随机选择上一时隙未受干扰的信道和干扰功率。在仿真过程中，首先在频谱感知信息完全正确的情况下，研究了算法的收敛性并对其进行性能评估。其次，在频谱感知结果存在误差的情况下，对算法的鲁棒性能进行分析讨论。仿真参数如表3所示。
表 3 仿真参数参数 值 信道总数M 6 蒙特卡罗仿真次数${\text{Mont}}$ 1000 时隙数$ {\text{Slots}} $ 10000 学习率$\alpha $ 0.5 折扣因子$\gamma $ 0.9 学习速率${\delta _{\text{l}}}$,${\delta _{\text{w}}}$ 0.1,0.03 信道切换代价${C_{\rm{h}}}$ 0.5 功率代价系数${C_{\rm{p}}}$ 0.5 干扰功率集合${P_{\rm{J}}}$ [2,4,6,8,10,12]×0–3 W 发射功率集合${P_{\rm{U}}}$ [7,14,21,28]×10–3 W 噪声功率${\sigma ^2}$ 10–3 W 如图2所示，本文针对扫频干扰、贪婪随机策略干扰、跟随式干扰、随机干扰4种典型干扰场景进行性能分析。假设一共有
$M = 6$ 个频率不重叠的通信信道，纵坐标表示信道，横坐标代表时隙。实心色块代表当前时隙存在干扰的信道，颜色深浅代表干扰功率的大小，颜色越深代表功率越大，白色代表当前时隙无干扰且不被占用的通信信道，网格块代表当前时隙正在通信的信道。其中，图2(a)表示扫频周期为$T = 3$ ，每个时隙存在$ m = 2 $ 个信道的扫频干扰；图2(b)为贪婪概率为$\varepsilon {\text{ = }}0.2$ 的贪婪随机策略干扰；图2(c)为跟随式干扰，当第1个时隙选取${f_5}$ 信道进行通信时，在第2个时隙就干扰${f_5}$ 信道；图2(d)为随机干扰。4.1 频谱感知结果完全正确的性能分析
为了对系统一段时间的性能进行统计，仿真过程中在每50个时隙内累积并统计一次奖励值。假设历史干扰检测所占用的信道和干扰功率完全正确，由图3(a)—图3(c)可知，当经历一段时间后，每种干扰模型下所得到的累积奖励值能够趋于稳定，可见算法具有收敛性。此外，还可以观察到WoLF-PHC比Q学习能更快地达到收敛，这说明该算法能够快速地学习干扰规律并迅速适应环境，采取最优策略使用户完成通信。在算法收敛后，WoLF-PHC和Q学习的性能相近，而随机策略性能相比这两者差很多。而由图3(d)所示，针对随机干扰，Q学习最终不能达到收敛，WoLF-PHC依然可以快速收敛。所以由仿真结果可知，在历史频谱感知结果完全正确的情况下，WoLF-PHC比Q学习可以获得更快的收敛速度，且性能也略优于Q学习，远好于随机策略。
4.2 频谱感知结果存在误差的性能分析
图4表示在扫频干扰的环境下，WoLF-PHC算法基于不同误检概率下的干扰规避性能，其中
$p$ 表示感知干扰所占信道错误的概率。由图4可以看出，当频谱感知结果存在误差时会对所提的干扰规避算法产生一定的影响。当频谱感知完全正确的情况下，干扰规避的性能优于频谱感知存在错误的情况，而且误检概率越大，干扰规避性能会越差，但随着时间的推移，不同误检概率的干扰规避性能几乎相近。而且，所提WoLF-PHC算法仍然能够实现收敛，对频谱感知误差具有一定的鲁棒性。5. 结论
本文主要在未知干扰环境下，研究了一种联合发射功率控制和动态信道接入的WoLF-PHC干扰规避方法。在4种典型的干扰环境下，通过对比基于Q学习的干扰规避方法、基于WoLF-PHC的干扰规避方法和随机干扰选择方法，可以看出前两种算法都比随机选择方法性能更优。所提的基于WoLF-PHC干扰规避方法的性能和收敛速度均比Q学习更好。进一步，在频谱感知结果存在误差的情况下对干扰规避性能的影响进行分析可知，频谱感知的误检概率越大，干扰规避性能会略差。在不同频谱感知误差情况下，所提WoLF-PHC算法仍然能够实现收敛，具有一定的鲁棒性。
-
表 1 基于Q学习的功率和信道选择策略
初始化：设k=0，确定初始状态$ {s^k} = (f_{\text{u}}^k,f_{\text{j}}^k) $，随机选择当前时隙通信信道$f_{\text{u}}^k$，并且进行频谱感知获取当前时隙的干扰信道$f_{\text{j}}^k$以及干扰功
率$ {p_{\text{j}}}^k $；初始化Q表为全0矩阵；设置学习率$\alpha $，折扣因子$\gamma $；学习过程：当$ k < K $时， (1) 利用贪婪策略选取动作$ {a^k} = ({f_{\text{u}}}^{k + 1},{p_{\text{u}}}^{k + 1}) $，然后再根据频谱感知结果，和选取的动作更新下一时隙的状态${s^{k{\text{ + }}1}} = (f_{\text{u}}^{k{\text{ + }}1},f_{\text{j}}^{k{\text{ + }}1})$，
计算出${\text{SIN}}{{\text{R}}^k}$和下一时隙反馈的奖励值$ {R^k} $；(2) 根据式(5)，更新Q表，$ k = k + 1 $。 
下载: 导出CSV
表 2 基于WoLF-PHC学习的功率和信道选择策略
初始化：折扣因子$\gamma $，学习率$\alpha $，学习速率${\delta _{\text{l}}}$, ${\delta _{\text{w}}}$；Q表为全0矩阵，$\pi \left( {s,a} \right){\text{ = } }{1}/{ { {\text{|} }A{\text{|} } } }$, $C({{s} }) = 0$； 学习过程：当$ k < K $时， (1) 根据当前策略$\pi (s,a)$和当前状态$s$选择动作$a$； (2) 获取下一时隙的状态$s$并计算$ R $，然后根据式(5)，更新Q表； (3) 更新$C({{s} }) \leftarrow C(s) + 1$，再根据式(8)和式(7)更新$\pi (s,a)$和$\bar \pi (s,a)$ (4) $ k{\text{ }} = {\text{ }}k + 1 $。
下载: 导出CSV
表 3 仿真参数
参数 值 信道总数M 6 蒙特卡罗仿真次数${\text{Mont}}$ 1000 时隙数$ {\text{Slots}} $ 10000 学习率$\alpha $ 0.5 折扣因子$\gamma $ 0.9 学习速率${\delta _{\text{l}}}$,${\delta _{\text{w}}}$ 0.1,0.03 信道切换代价${C_{\rm{h}}}$ 0.5 功率代价系数${C_{\rm{p}}}$ 0.5 干扰功率集合${P_{\rm{J}}}$ [2,4,6,8,10,12]×0–3 W 发射功率集合${P_{\rm{U}}}$ [7,14,21,28]×10–3 W 噪声功率${\sigma ^2}$ 10–3 W
下载: 导出CSV
-
[1] ZOU Yulong, ZHU Jia, WANG Xianbin, et al. A survey on wireless security: Technical challenges, recent advances, and future trends[J]. Proceedings of the IEEE, 2016, 104(9): 1727–1765. doi: 10.1109/JPROC.2016.2558521 [2] GROVER K, LIM A, and YANG Qing. Jamming and anti-jamming techniques in wireless networks: A survey[J]. International Journal of Ad Hoc and Ubiquitous Computing, 2014, 17(4): 197–215. doi: 10.1504/IJAHUC.2014.066419 [3] LI Fang, XIONG Jun, ZHAO Xiaodi, et al. An improved FCME algorithm based on differential spectrum envelope for interference detection in satellite communication systems[C]. The 5th International Conference on Computer and Communication Systems (ICCCS), Shanghai, China, 2020: 874–879. [4] SUTTON R S and BARTO A G. Reinforcement Learning: An Introduction[M]. Cambridge: MIT Press, 1998: 216–224. [5] KONG Lijun, XU Yuhua, ZHANG Yuli, et al. A reinforcement learning approach for dynamic spectrum anti-jamming in fading environment[C]. The IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 2018: 51–58. [6] SLIMENI F, CHTOUROU Z, SCHEERS B, et al. Cooperative Q-learning based channel selection for cognitive radio networks[J]. Wireless Networks, 2019, 25(7): 4161–4171. doi: 10.1007/s11276-018-1737-9 [7] WANG Beibei, WU Yongle, LIU K J R, et al. An anti-jamming stochastic game for cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(4): 877–889. doi: 10.1109/JSAC.2011.110418 [8] GWON Y, DASTANGOO S, FOSSA C, et al. Competing mobile network game: Embracing antijamming and jamming strategies with reinforcement learning[C]. 2013 IEEE Conference on Communications and Network Security (CNS), National Harbor, USA, 2013: 28–36. [9] SLIMENI F, SCHEERS B, CHTOUROU Z, et al. Jamming mitigation in cognitive radio networks using a modified Q-learning algorithm[C]. 2015 IEEE International Conference on Military Communications and Information Systems (ICMCIS), Cracow, Poland, 2015: 1–7. [10] MPITZIOPOULOS A, GAVALAS D, KONSTANTOPOULOS C, et al. A survey on jamming attacks and countermeasures in WSNs[J]. IEEE Communications Surveys & Tutorials, 2009, 11(4): 42–56. doi: 10.1109/SURV.2009.090404 [11] ZHANG Yuli, XU Yuhua, XU Yitao, et al. A multi-leader one-follower stackelberg game approach for cooperative anti-jamming: No Pains, No Gains[J]. IEEE Communications Letters, 2018, 22(8): 1680–1683. doi: 10.1109/LCOMM.2018.2843374 [12] HANAWAL M K, ABDEL-RAHMAN M J, and KRUNZ M. Joint adaptation of frequency hopping and transmission rate for anti-jamming wireless systems[J]. IEEE Transactions on Mobile Computing, 2016, 15(9): 2247–2259. doi: 10.1109/TMC.2015.2492556 [13] HANAWAL M K, ABDEL-RAHMAN M J, and KRUNZ M. Game theoretic anti-jamming dynamic frequency hopping and rate adaptation in wireless systems[C]. The 12th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Hammamet, Tunisia, 2014: 247–254. [14] LI Yangyang, XU Yitao, WANG Ximing, et al. Power and frequency selection optimization in anti-jamming communication: A deep reinforcement learning approach[C]. The IEEE 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 2019: 815–820. [15] XIAO Liang, JIANG Donghua, XU Dongjin, et al. Two-dimensional antijamming mobile communication based on reinforcement learning[J]. IEEE Transactions on Vehicular Technology, 2018, 67(10): 9499–9512. doi: 10.1109/TVT.2018.2856854 [16] PEI Xufang, WANG Ximing, YAO Junnan, et al. Joint time-frequency anti-jamming communications: A reinforcement learning approach[C]. The 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi'an, China, 2019: 1–6. [17] BOWLING M and VELOSO M. Multiagent learning using a variable learning rate[J]. Artificial Intelligence, 2002, 136(2): 215–250. doi: 10.1016/S0004-3702(02)00121-2 期刊类型引用(6)
1. 陈帅明. 基于深度强化学习的通信动态抗干扰决策模型. 电脑知识与技术. 2024(09): 89-92 . 
百度学术2. 韩晓娱，刘昊昱，张世层，王丽冲. LEO卫星系统对GSO卫星系统干扰规避技术研究. 计算机与网络. 2024(01): 74-79 . 百度学术3. 周成，林茜，马丛珊，应涛，满欣. 通信干扰信道和功率智能决策算法. 电子与信息学报. 2024(10): 3957-3965 . 
本站查看4. 高科婕，朱勇刚，张凯，周展阳. 资源受限下基于改进Q学习的干扰自适应采样. 电子信息对抗技术. 2024(06): 26-34 . 百度学术5. 肖亮，陈顺，王烁华，吕泽芳，杨和林. 面向数字孪生的智能无线通信抗干扰技术. 移动通信. 2023(06): 8-13 . 百度学术6. 李博扬，刘洋，万诺天，许魁，夏晓晨，张月月，张咪. 基于强化学习的无人机电磁干扰感知与抗干扰传输方法. 电讯技术. 2023(12): 1855-1861 . 百度学术其他类型引用(3)
-
下载:
百度学术
计量
- 文章访问数: 884
- HTML全文浏览量: 1103
- PDF下载量: 218
- 被引次数: 9
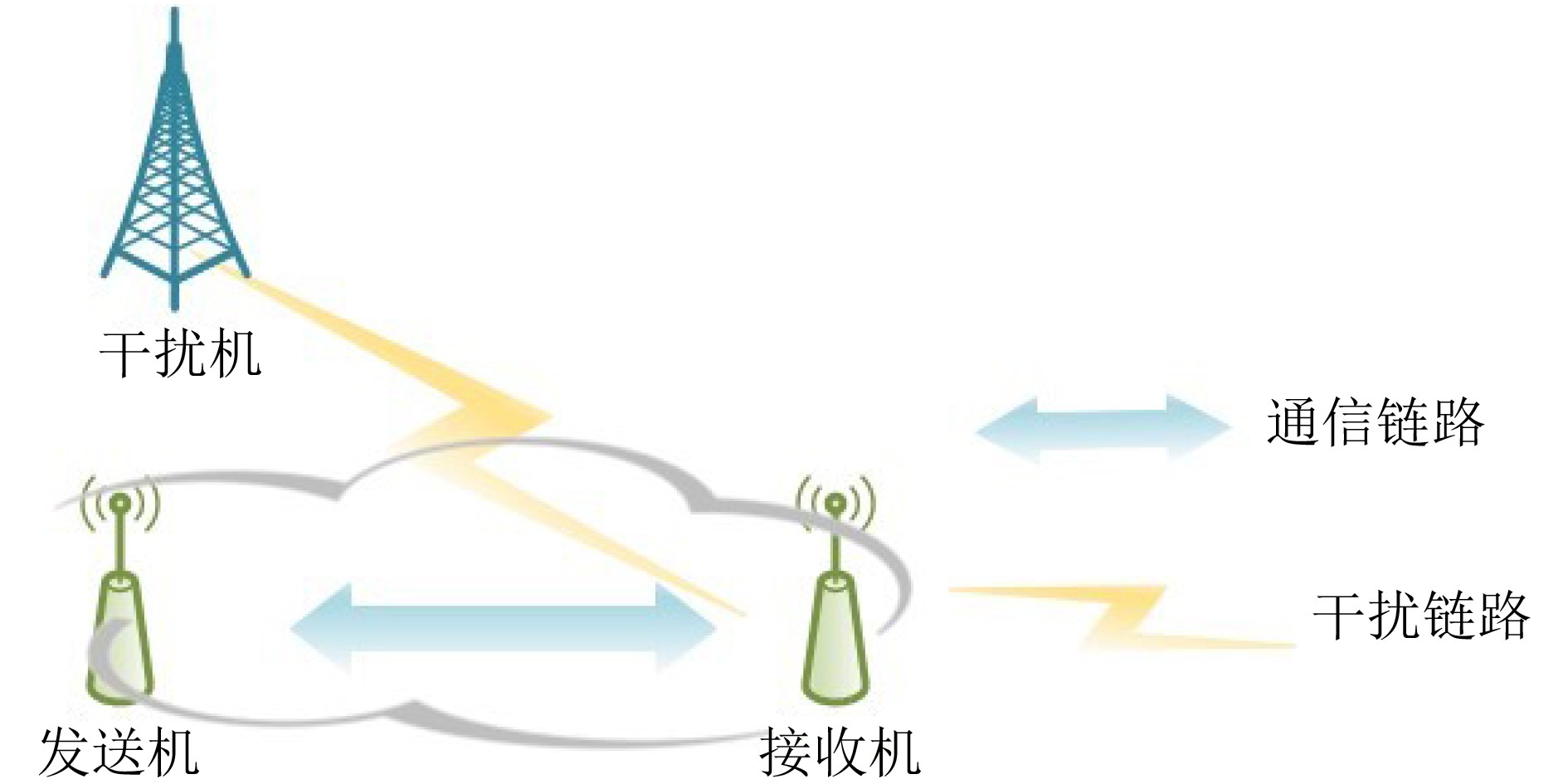
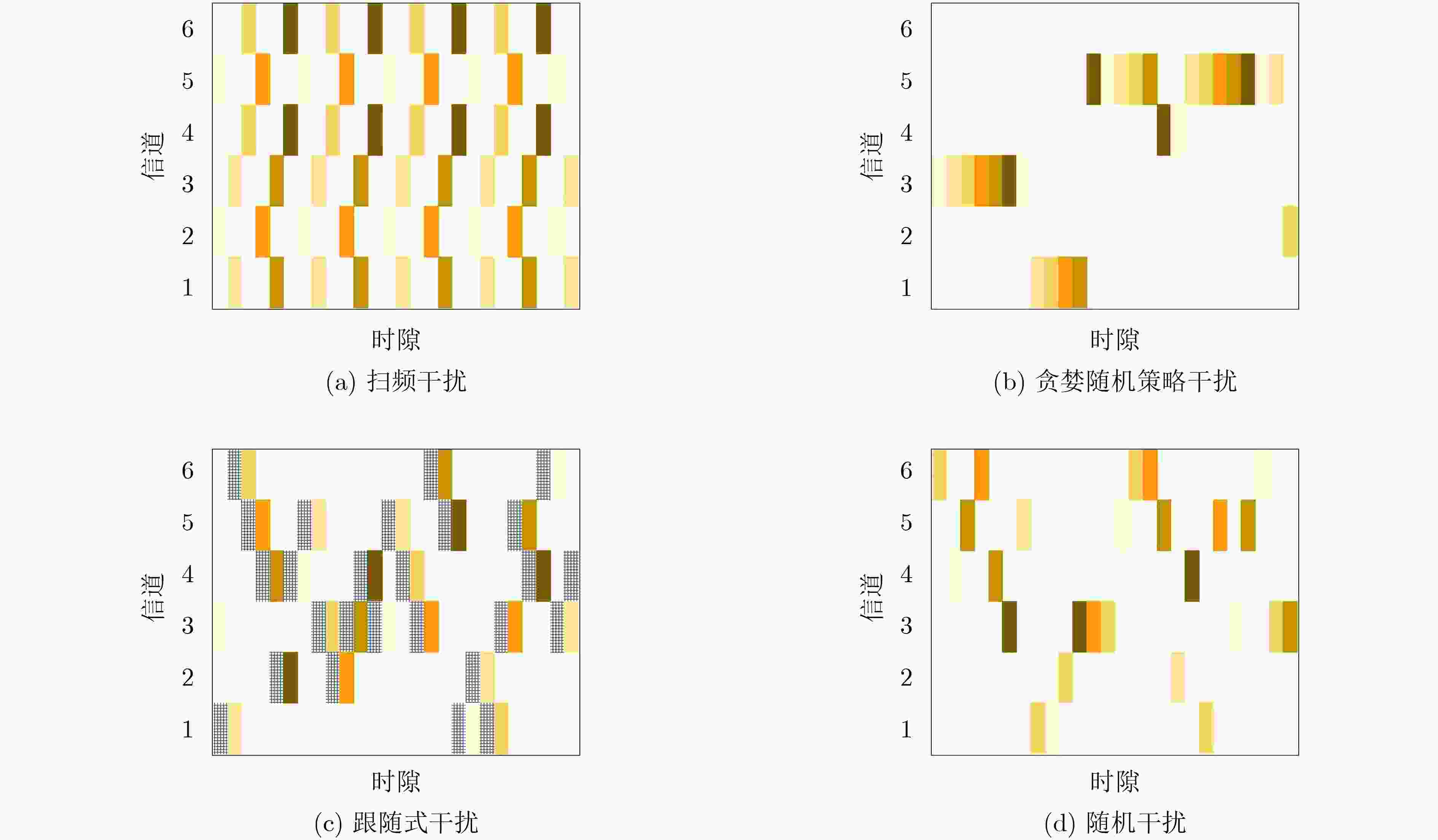
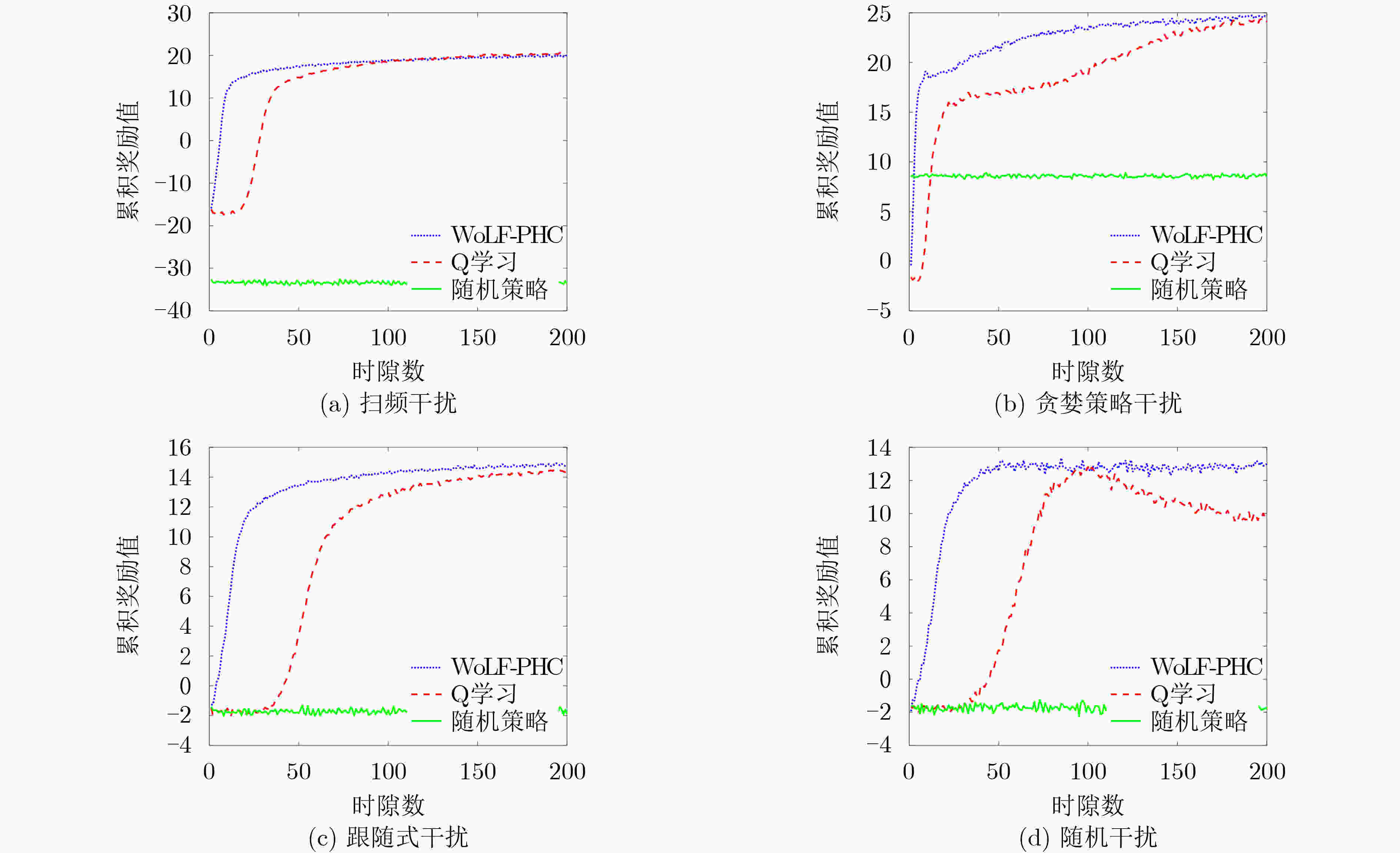
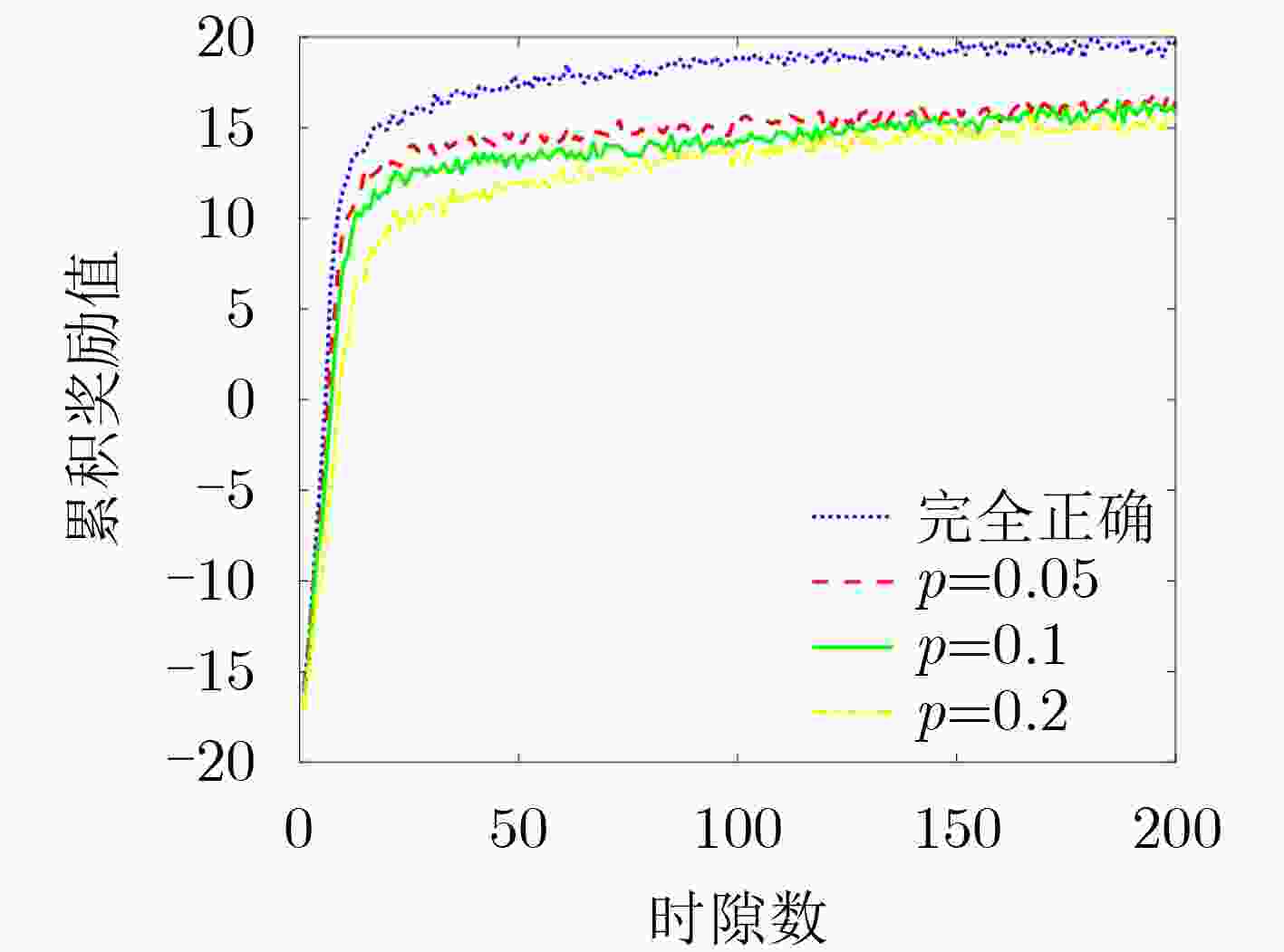
下载:
