一种基于旋转不变子空间算法的非模糊参数配对方法

揭允康; 叶晓东; 王昊; 李莉; 陶诗飞

doi:10.11999/JEIT210942

一种基于旋转不变子空间算法的非模糊参数配对方法

doi: 10.11999/JEIT210942

南京理工大学电子工程与光电技术学院南京 210094

基金项目: 国家自然科学基金(61701240)，中央高校基本科研业务费专项资金(30918011317)，国家重点实验室基金(CEMEE2022K0102B)

详细信息

作者简介:
揭允康：男，博士生，研究方向为稀疏阵列信号处理、DOA估计

叶晓东：男，副教授，研究方向为通信理论与技术、随机信号理论与应用、信号获取与处理、现代信号处理

王昊：男，副研究员，研究方向为数字波束形成天线系统、多功能雷达天线系统、新型通信天线系统

李莉：女，硕士生，研究方向为阵列自适应波束形成

陶诗飞：男，副研究员，研究方向为雷达目标特性分析、雷达成像及信号处理、计算电磁学

通讯作者:
陶诗飞　s.tao@njust.edu.cn

中图分类号: TN97
计量
- 文章访问数: 861
- HTML全文浏览量: 381
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-06
- 修回日期: 2021-11-15
- 录用日期: 2021-11-18
- 网络出版日期: 2021-11-20
- 刊出日期: 2022-12-16

A Non-fuzzy Parameter Pairing Method Based on Estimating Signal Parameter via Rotational Invariance Techniques

School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

Funds: The National Natural Science Foundation of China (61701240), The Fundamental Reasearch Funds for the Central Universities (30918011317), The State Key Laboratory Foundation of CEMEE (CEMEE2022K0102B)

摘要

摘要: 针对多维旋转不变子空间算法(ESPRIT)信号参数估计存在失配的问题，该文提出一种基于特征值分维的参数配对方法。该方法首先对包含待估计参数信息的多维特征值进行线性组合并构造判断矩阵，再根据矩阵维数对应关系进行配对。相比于其他配对算法，该文提出的算法结构简单，没有模糊参数，在特定情况下具有较高的鲁棒性，能实现参数的自动配对。最后通过对比仿真验证了该文配对算法的优越性。
- 频率估计 /
- 旋转不变子空间算法 /
- 参数配对 /
- 非模糊
Abstract: There are some mismatches for the estimation of signal parameters in mult-dimention Estimating Signal Parameter via Rotational Invariance Techniques (ESPRIT) algorithm. In this paper, a parameter pairing method based on eigenvalue fractal dimension is proposed. By linearly combining the eigenvalues and constructing a judgment matrix, the parameters are paired according to the corresponding relationship of matrix dimension. In contrast to other pairing algorithms, the proposed algorithm can achieve automatic pairing with low complexity, non-fuzzy parameters and higher robustness. Several examples are given to demonstrate the effectiveness of the proposed algorithm.
- Frequency estimation /
- Estimating Signal Parameter via Rotational Invariance Techniques (ESPRIT) /
- Parameter pairing /
- Non-fuzzy

HTML全文

图 1 本文算法的配对结果

下载: 全尺寸图片幻灯片

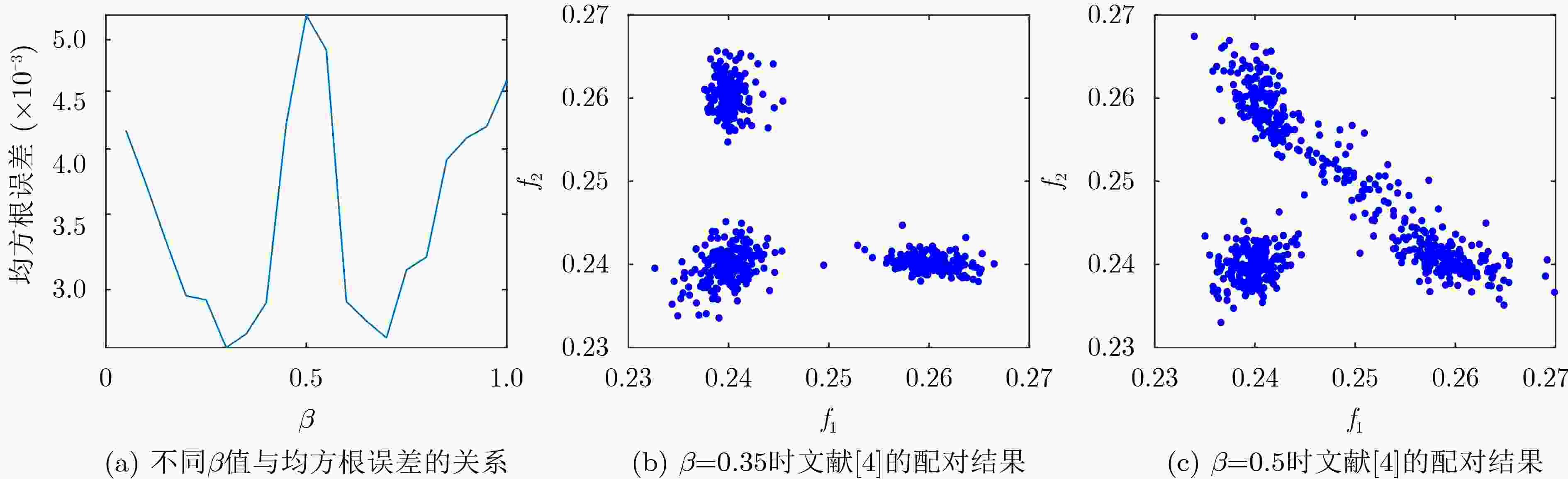
图 2 文献[4]中不同β取值的配对结果

下载: 全尺寸图片幻灯片

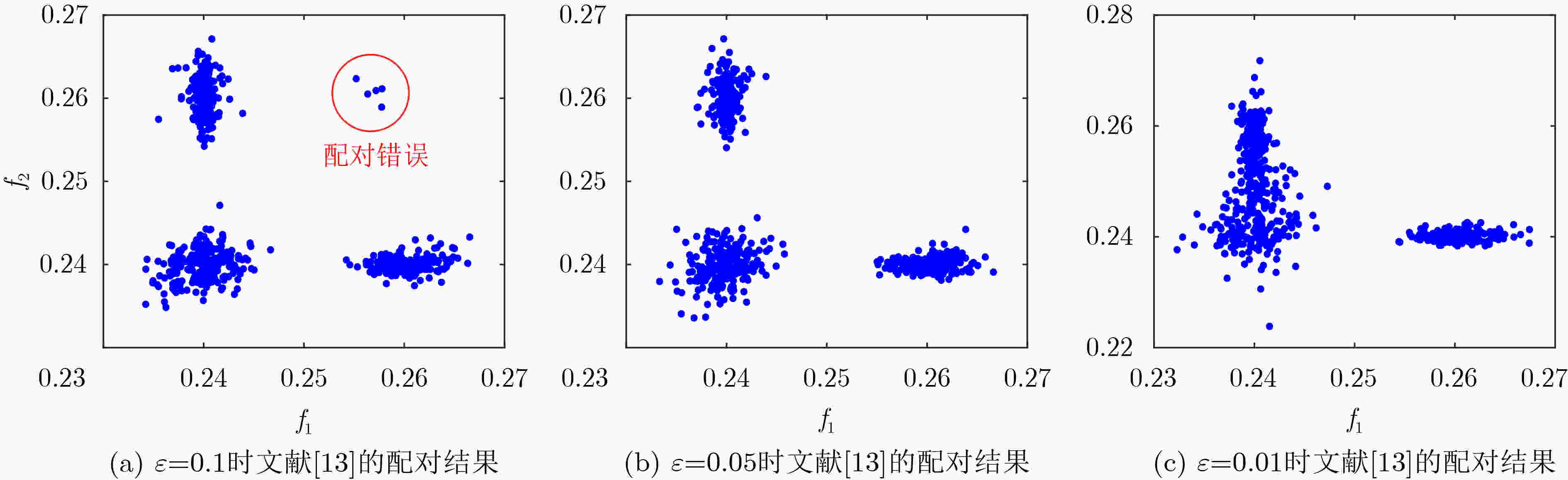
图 3 文献[13]中不同ε取值的配对结果

下载: 全尺寸图片幻灯片

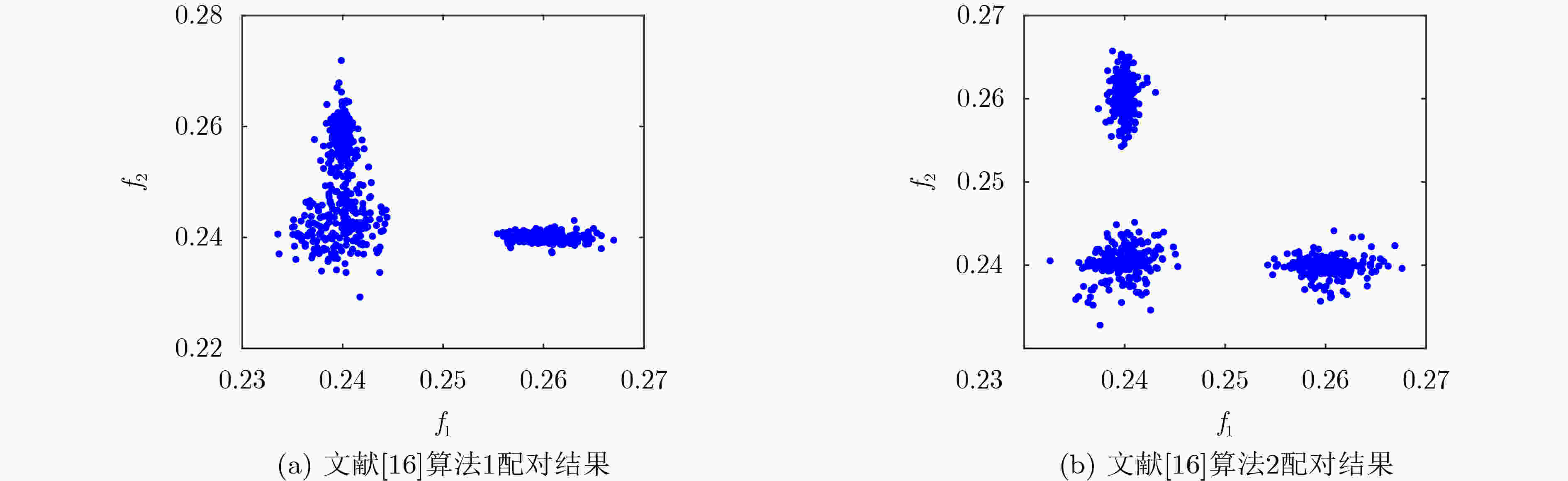
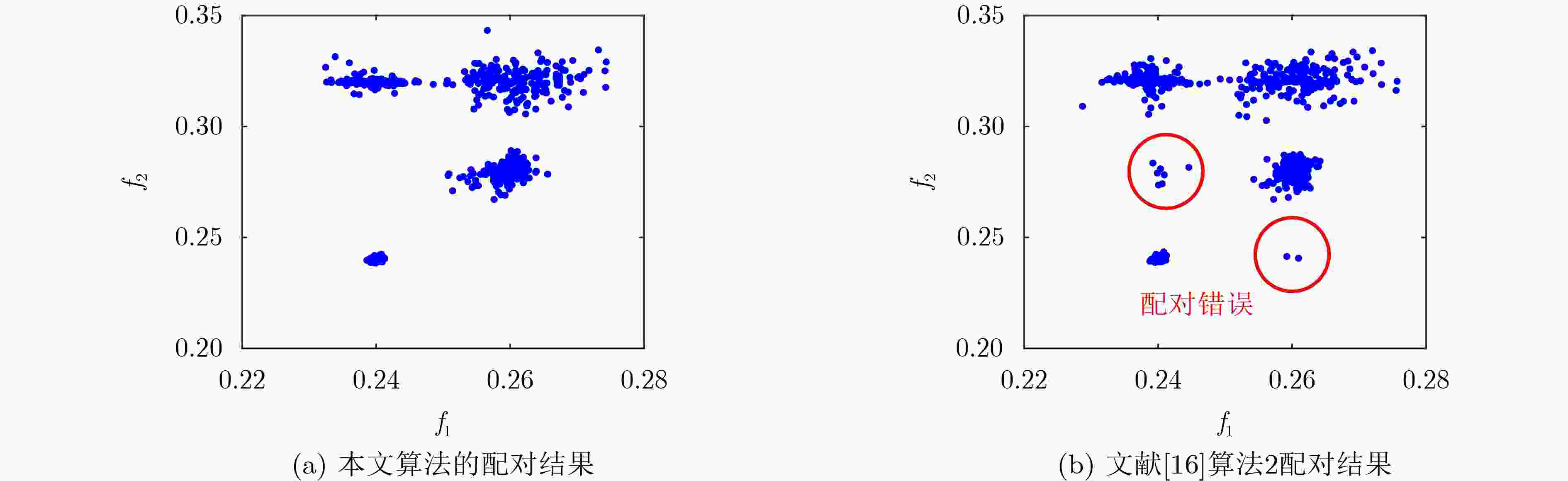
图 4 文献[16]算法配对结果

下载: 全尺寸图片幻灯片

图 5 不同算法均方根误差随SNR的变化

下载: 全尺寸图片幻灯片

图 6 不同算法配对结果

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	BOURI M. A novel fast high resolution MUSIC algorithm[C]. 2012 IEEE Workshop on Signal Processing Systems, Quebec City, Canada, 2012: 237–242.
[2]	王伟, 王晓萌, 李欣, 等. 基于MUSIC算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2014, 36(8): 1954–1959. doi: 10.3724/SP.J.1146.2013.01281 WANG Wei, WANG Xiaomeng, LI Xin, et al. Reduced-dimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics &Information Technology, 2014, 36(8): 1954–1959. doi: 10.3724/SP.J.1146.2013.01281
[3]	姚昕彤, 王玉文, 刘奇, 等. 基于MUSIC及其改进算法的DOA估计研究[J]. 通信技术, 2021, 54(6): 1363–1369. doi: 10.3969/j.issn.1002-0802.2021.06.012 YAO Xintong, WANG Yuwen, LIU Qi, et al. Research on DOA estimation based on MUSIC and its improved algorithm[J]. Communications Technology, 2021, 54(6): 1363–1369. doi: 10.3969/j.issn.1002-0802.2021.06.012
[4]	ROUQUETTE S and NAJIM M. Estimation of frequencies and damping factors by two-dimensional ESPRIT type methods[J]. IEEE Transactions on Signal Processing, 2001, 49(1): 237–245. doi: 10.1109/78.890367
[5]	CHENG Qian. A simple modification of ESPRIT[J]. IEEE Signal Processing Letters, 2018, 25(8): 1256–1260. doi: 10.1109/LSP.2018.2851385
[6]	DONG Yangyang, DONG Chunxi, XU Jin, et al. Computationally efficient 2-D DOA estimation for L-shaped array with automatic pairing[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1669–1672. doi: 10.1109/LAWP.2016.2521785
[7]	梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8): 1828–1835. doi: 10.11999/JEIT141295 LIANG Hao, CUI Chen, DAI Lin, et al. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics &Information Technology, 2015, 37(8): 1828–1835. doi: 10.11999/JEIT141295
[8]	张小宽, 郑舒予, 奚之飞, 等. 基于改进LS-ESPRIT算法的GTD模型参数估计与RCS重构[J]. 电子与信息学报, 2020, 42(10): 2493–2499. doi: 10.11999/JEIT190747 ZHANG Xiaokuan, ZHENG Shuyu, XI Zhifei, et al. GTD model parameters estimation and RCS reconstruction based on the improved LS-ESPRIT algorithm[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2493–2499. doi: 10.11999/JEIT190747
[9]	HUA Y. Estimating two-dimensional frequencies by matrix enhancement and matrix pencil[J]. IEEE Transactions on Signal Processing, 1992, 40(9): 2267–2280. doi: 10.1109/78.157226
[10]	王秀, 常青, 王耀力. 基于L型阵列酉变换矩阵重构的二维DOA估计[J]. 电信科学, 2018, 34(7): 110–117. WANG Xiu, CHANG Qing, and WANG Yaoli. Two-dimensional DOA estimation of unitary transformation matrix reconstruction based on L-shaped array[J]. Telecommunications Science, 2018, 34(7): 110–117.
[11]	CHEN Weiyang, ZHANG Xiaofei, and JIANG Chi. Two-dimensional DOA estimation for planar array using a successive propagator method[J]. Journal of Circuits, Systems and Computers, 2019, 28(10): 1950161. doi: 10.1142/S0218126619501615
[12]	AHMED T and ZHANG Xiaofei. Higher-order unitary propagator method for 2D-DOA estimation of non-circular sources via uniform rectangular array[J]. Digital Signal Processing, 2020, 100: 102700. doi: 10.1016/j.dsp.2020.102700
[13]	CHEN Fangjiong, FUNG C C, KOK C W, et al. Estimation of two-dimensional frequencies using modified matrix pencil method[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 718–724. doi: 10.1109/TSP.2006.885813
[14]	林俊发. 自动配对的二维矩阵束信号频率参数估计[J]. 电子元器件与信息技术, 2020, 4(7): 32–34,61. doi: 10.19772/j.cnki.2096-4455.2020.7.016 LIN Junfa. Two dimensional signal parameter estimation with automatic pairing by matrix pencil method[J]. Electronic Component and Information Technology, 2020, 4(7): 32–34,61. doi: 10.19772/j.cnki.2096-4455.2020.7.016
[15]	ZOLTOWSKI M D, HAARDT M, and MATHEWS C P. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT[J]. IEEE Transactions on Signal Processing, 1996, 44(2): 316–328. doi: 10.1109/78.485927
[16]	杨力强, 刘声, 杨力生, 等. 二维ESPRIT类算法中参数配对的新方法[J]. 无线电工程, 2014, 44(11): 23–25,33. doi: 10.3969/j.issn.1003-3106.2014.11.07 YANG Liqiang, LIU Sheng, YANG Lisheng, et al. A new parameter matching method for 2D ESPRIT algorithm[J]. Radio Engineering, 2014, 44(11): 23–25,33. doi: 10.3969/j.issn.1003-3106.2014.11.07
[17]	SAHNOUN S, USEVICH K, and COMON P. Multidimensional ESPRIT for damped and undamped signals: Algorithm, computations, and perturbation analysis[J]. IEEE Transactions on Signal Processing, 2017, 65(22): 5897–5910. doi: 10.1109/TSP.2017.2736512
[18]	ZHENG Shuyu, ZHANG Xiaokuan, ZHAO Weichen, et al. Parameter estimation of GTD model and RCS extrapolation based on a modified 3D-ESPRIT algorithm[J]. Journal of Systems Engineering and Electronics, 2020, 31(6): 1206–1215. doi: 10.23919/JSEE.2020.000065
[19]	GU Pengfei, HE Z, XU Juan, et al. Design of wide scanning sparse planar array using both matrix-pencil and space-mapping methods[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(2): 140–144. doi: 10.1109/LAWP.2020.3039995
[20]	刘玲, 曾孝平, 曾浩. 基于奇异值的信源数估计方法[J]. 计算机工程, 2009, 35(12): 34–37. doi: 10.3969/j.issn.1000-3428.2009.12.012 LIU Ling, ZENG Xiaoping, and ZENG Hao. Signal source number estimation method based on singular value[J]. Computer Engineering, 2009, 35(12): 34–37. doi: 10.3969/j.issn.1000-3428.2009.12.012