基于变步长约瑟夫遍历和DNA动态编码的图像加密算法的安全性分析

冯伟; 张靖; 秦振涛; 何怡刚

doi:10.11999/JEIT210791

基于变步长约瑟夫遍历和DNA动态编码的图像加密算法的安全性分析

doi: 10.11999/JEIT210791

冯伟¹,
张靖^1, ,,
秦振涛¹,
何怡刚²

1.
攀枝花学院数学与计算机学院攀枝花 617000
2.
武汉大学电气与自动化学院武汉 430072

基金项目: 国家自然科学基金(51977153, 51637004)，教育部科技发展中心项目(2018A0105)

详细信息

作者简介:
冯伟：男，副教授，博士，研究方向为多媒体信息技术与安全

张靖：男，教授，博士，研究方向为大数据安全与隐私保护

秦振涛：男，教授，博士，研究方向为图像处理与识别

何怡刚：男，教授，博士，研究方向为电气信息处理技术

通讯作者:
张靖　zjpzh@tom.com

中图分类号: TN918; TP309
计量
- 文章访问数: 575
- HTML全文浏览量: 291
- PDF下载量: 93
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-06
- 修回日期: 2022-03-29
- 网络出版日期: 2022-04-21
- 刊出日期: 2022-10-19

Cryptanalysis of Image Encryption Algorithm Based on Variable Step Length Josephus Traversing and DNA Dynamic Encoding

1.
School of Mathematics and Computer Science, Panzhihua University, Panzhihua 617000, China
2.
School of Electrical Engineering and Automation, Wuhan University, Wuhan 430072, China

Funds: The National Natural Science Foundation of China (51977153, 51637004), The Science and Technology Development Center Project of Chinese Ministry of Education (2018A0105)

摘要

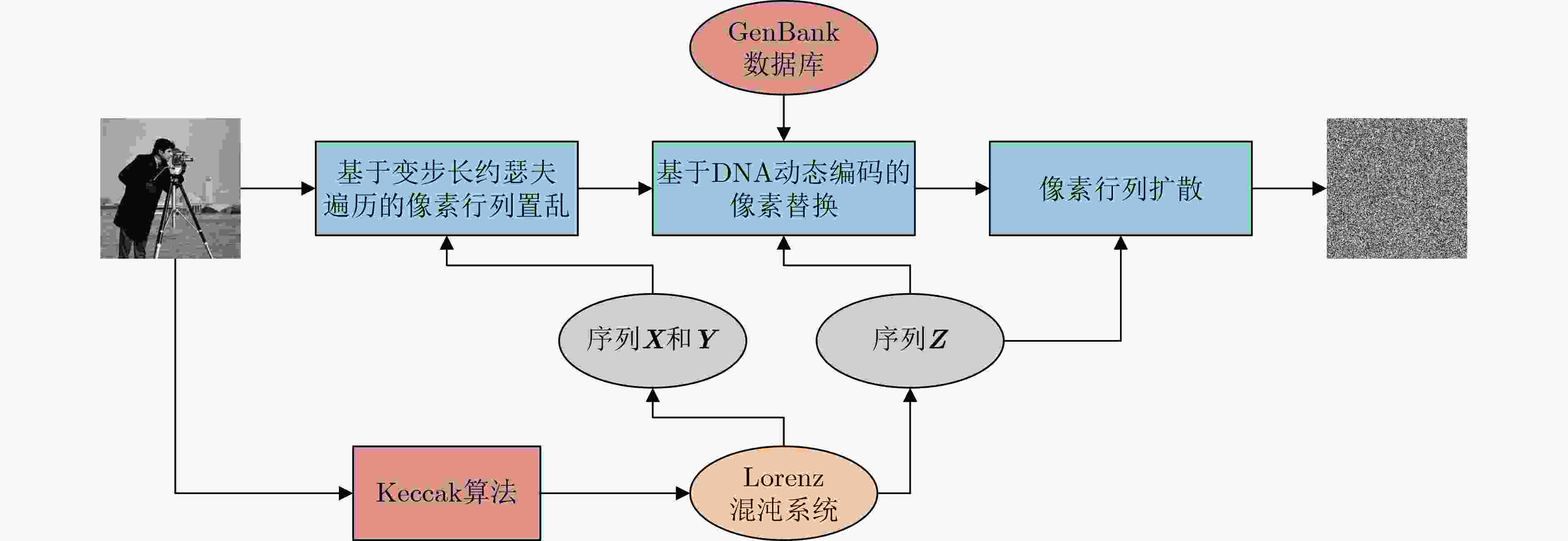
摘要: 近年来，不断有新的图像加密算法被提出，其安全性却未得到充分的分析和验证。该文对一种最新报道的图像加密算法的安全性进行了分析。所分析算法通过基于变步长约瑟夫遍历的像素置乱、基于DNA动态编码的像素替换及像素行列扩散来完成图像加密。分析表明，该算法的秘密密钥设计不具有实用性，加密过程也存在缺陷。在选择明文攻击条件下，对该算法的加密过程进行了密码分析，并提出了相应的攻击算法。仿真实验和理论分析确认了所提攻击算法的有效性与可行性。最后，针对所分析算法及部分图像加密算法中存在的问题，提出了改进建议。
- 图像加密 /
- 安全性 /
- 密码分析 /
- 选择明文攻击
Abstract: In recent years, new image encryption algorithms have been continuously proposed, but their security has not been fully analyzed and verified. The security of a newly reported image encryption algorithm is analyzed in this paper. The analyzed algorithm achieves the image encryption through pixel scrambling based on variable step length Josephus traversing, pixel substitution based on DNA dynamic encoding, and pixel diffusion in row and column directions. Analysis shows that the secret key design of this algorithm is not practical, and its encryption process also has defects. Under the condition of chosen-plaintext attack, the encryption process of this algorithm is cryptanalyzed, and a corresponding attack algorithm is proposed. Simulation experiments and theoretical analysis confirm the effectiveness and feasibility of the proposed attack algorithm. Finally, in view of issues in the analyzed algorithm and some image encryption algorithms, several suggestions for improvement are given.
- Image encryption /
- Security /
- Cryptanalysis /
- Chosen-plaintext attack

HTML全文

图 1 IEA-VJD的加密流程图

下载: 全尺寸图片幻灯片

表 1 像素扩散效果消除算法

输入：大小为M×N的密文图像C。
(1) 当i等于3到M时，重复执行操作C⁽¹⁾(i, :) = C(i, :)$\oplus $C(i–1, :) 　　 $\oplus $C(i–2, :)；
(2) 执行操作C⁽¹⁾(2, :) = C(2, :)$\oplus $C(1, :)$\oplus $C⁽¹⁾(M, :)；
(3) 执行操作C⁽¹⁾(1, :) = C(1, :)$\oplus $C⁽¹⁾(M, :)$\oplus $C⁽¹⁾(M–1, :)；
(4) 当j等于3到N时，重复执行操作C⁽²⁾(:, j) = C⁽¹⁾(:, j)$\oplus $C⁽¹⁾(:, 　　 j–1)$\oplus $C⁽¹⁾(:, j–2)；
(5) 执行操作C⁽²⁾(:, 2) = C⁽¹⁾(:, 2)$\oplus $C⁽¹⁾(:, 1)$\oplus $C⁽²⁾(:, N)；
(6) 执行操作C⁽²⁾(:, 1) = C⁽¹⁾(:, 1)$\oplus $C⁽²⁾(:, N)$\oplus $C⁽²⁾(:, N–1)。
输出：已消除像素扩散效果的密文图像C⁽²⁾。

下载: 导出CSV

表 2 选择明文攻击算法

输入：需恢复其明文图像的密文图像C，大小为M×N。
(1) 当v等于1到256时，重复执行操作：
(a) 构建像素值为v–1的单一像素值明文图像P^(v–1)，加密获　　　　得其对应的密文图像C^(v–1)。
(b) 调用表1算法消除C^(v–1)的像素扩散效果，将C^(v–1)拉伸成　　　　一维行向量，令E^(S)(v, :) = C^(v–1)；
(2) 确定获取等价置乱矩阵E^(P)所需明文图像数量q。
(3) 当w等于1到q时，重复执行操作：
(a) 构建获取E^(P)所需的第w张选择明文图像P^(w)，加密获得　　　　其对应的密文图像C^(w)。
(b) 调用表1算法消除C^(w)的像素扩散效果；
(c) 利用E^(S)消除C^(w)的像素替换效果；
(d) 在C^(w)中查找每个明文图像非0值像素的对应位置，并将　　　　其保存至E^(P)；
(4) 调用表1算法消除C的像素扩散效果，得到C⁽²⁾；
(5) 利用E^(S)消除C⁽²⁾的像素替换效果，得到C⁽³⁾；
(6) 利用E^(P)消除C⁽³⁾的像素置乱效果，得到P^(R)。
输出：恢复的明文图像P^(R)以及E^(S)和E^(P)。

下载: 导出CSV

表 3 攻击算法有效性测试结果

明文图像	大小	密文图像	消除扩散效果	消除替换效果	消除置乱效果
	256×256
	256×256
	512×512
	512×512

下载: 导出CSV

表 4 攻击算法各攻击步骤平均耗时(s)

输入规模	消除扩散效果	获取等价替换矩阵	消除替换效果	获取等价置乱矩阵	消除置换效果
128×128	0.0025	0.8627	0.0304	1.6027	0.0002
256×256	0.0074	2.4619	0.1164	23.9314	0.0011
512×512	0.0294	9.1939	0.4909	392.8737	0.0049

下载: 导出CSV

参考文献(20)

[1]	ÖZKAYNAK F. Brief review on application of nonlinear dynamics in image encryption[J]. Nonlinear Dynamics, 2018, 92(2): 305–313. doi: 10.1007/s11071-018-4056-x
[2]	FENG Wei, HE Yigang, LI Hongmin, et al. Image encryption algorithm based on discrete logarithm and memristive chaotic system[J]. The European Physical Journal Special Topics, 2019, 228(10): 1951–1967. doi: 10.1140/epjst/e2019-800209-3
[3]	HUA Zhongyun, JIN Fan, XU Binxuan, et al. 2D logistic-sine-coupling map for image encryption[J]. Signal Processing, 2018, 149: 148–161. doi: 10.1016/j.sigpro.2018.03.010
[4]	陈艳浩, 刘中艳, 周丽宴. 基于差异混合掩码与混沌Gyrator变换的光学图像加密算法[J]. 电子与信息学报, 2019, 41(4): 888–895. doi: 10.11999/JEIT180456 CHEN Yanhao, LIU Zhongyan, and ZHOU Liyan. Optical image encryption algorithm based on differential mixed mask and chaotic Gyrator transform[J]. Journal of Electronics &Information Technology, 2019, 41(4): 888–895. doi: 10.11999/JEIT180456
[5]	李付鹏, 刘敬彪, 王光义, 等. 基于混沌集的图像加密算法[J]. 电子与信息学报, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344 LI Fupeng, LIU Jingbiao, WANG Guangyi, et al. An image encryption algorithm based on chaos set[J]. Journal of Electronics &Information Technology, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344
[6]	ZHAO Ruoyu, ZHANG Yushu, XIAO Xiangli, et al. TPE2: Three-pixel exact thumbnail-preserving image encryption[J]. Signal Processing, 2021, 183: 108019. doi: 10.1016/j.sigpro.2021.108019
[7]	肖成龙, 孙颖, 林邦姜, 等. 基于神经网络与复合离散混沌系统的双重加密方法[J]. 电子与信息学报, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213 XIAO Chenglong, SUN Ying, LIN Bangjiang, et al. Double encryption method based on neural network and composite discrete chaotic system[J]. Journal of Electronics &Information Technology, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213
[8]	LI Hongmin, LI Tie, FENG Wei, et al. A novel image encryption scheme based on non-adjacent parallelable permutation and dynamic DNA-level two-way diffusion[J]. Journal of Information Security and Applications, 2021, 61: 102844. doi: 10.1016/j.jisa.2021.102844
[9]	郭媛, 周艳艳, 敬世伟. 基于图像重组和比特置乱的多图像加密[J]. 光子学报, 2020, 49(4): 0410002. doi: 10.3788/gzxb20204904.0410002 GUO Yuan, ZHOU Yanyan, and JING Shiwei. Multiple-image encryption based on image recombination and bit scrambling[J]. Acta Photonica Sinica, 2020, 49(4): 0410002. doi: 10.3788/gzxb20204904.0410002
[10]	LI Chengqing, ZHANG Yun, and XIE E Y. When an attacker meets a cipher-image in 2018: A year in review[J]. Journal of Information Security and Applications, 2019, 48: 102361. doi: 10.1016/j.jisa.2019.102361
[11]	闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178 MIN Fuhong, WANG Zhulin, WANG Enrong, et al. New memristor chaotic circuit and its application to image encryption[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178
[12]	FRIDRICH J. Symmetric ciphers based on two-dimensional chaotic maps[J]. International Journal of Bifurcation and Chaos, 1998, 8(6): 1259–1284. doi: 10.1142/S021812749800098X
[13]	WU Xiangjun, WANG Kunshu, WANG Xingyuan, et al. Color image DNA encryption using NCA map-based CML and one-time keys[J]. Signal Processing, 2018, 148: 272–287. doi: 10.1016/j.sigpro.2018.02.028
[14]	CHAI Xiuli, GAN Zhihua, YUAN Ke, et al. A novel image encryption scheme based on DNA sequence operations and chaotic systems[J]. Neural Computing and Applications, 2019, 31(1): 219–237. doi: 10.1007/s00521-017-2993-9
[15]	ZEFREH E Z. An image encryption scheme based on a hybrid model of DNA computing, chaotic systems and hash functions[J]. Multimedia Tools and Applications, 2020, 79(33): 24993–25022. doi: 10.1007/s11042-020-09111-1
[16]	JOLFAEI A, WU Xinwen, and MUTHUKKUMARASAMY V. On the security of permutation-only image encryption schemes[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(2): 235–246. doi: 10.1109/TIFS.2015.2489178
[17]	FENG Wei and HE Yigang. Cryptanalysis and improvement of the hyper-chaotic image encryption scheme based on DNA encoding and scrambling[J]. IEEE Photonics Journal, 2018, 10(6): 7909215. doi: 10.1109/JPHOT.2018.2880590
[18]	PREISHUBER M, HÜTTER T, KATZENBEISSER S, et al. Depreciating motivation and empirical security analysis of chaos-based image and video encryption[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(9): 2137–2150. doi: 10.1109/TIFS.2018.2812080
[19]	CHEN Junxin, CHEN Lei, and ZHOU Yicong. Cryptanalysis of a DNA-based image encryption scheme[J]. Information Sciences, 2020, 520: 130–141. doi: 10.1016/j.ins.2020.02.024
[20]	牛莹, 张勋才. 基于变步长约瑟夫遍历和DNA动态编码的图像加密算法[J]. 电子与信息学报, 2020, 42(6): 1383–1391. doi: 10.11999/JEIT190849 NIU Ying and ZHANG Xuncai. Image encryption algorithm of based on variable step length Josephus traversing and DNA dynamic coding[J]. Journal of Electronics &Information Technology, 2020, 42(6): 1383–1391. doi: 10.11999/JEIT190849