Research on Satellite Single-mixed Signal Modulation Recognition Based on Joint Feature Parameters
-
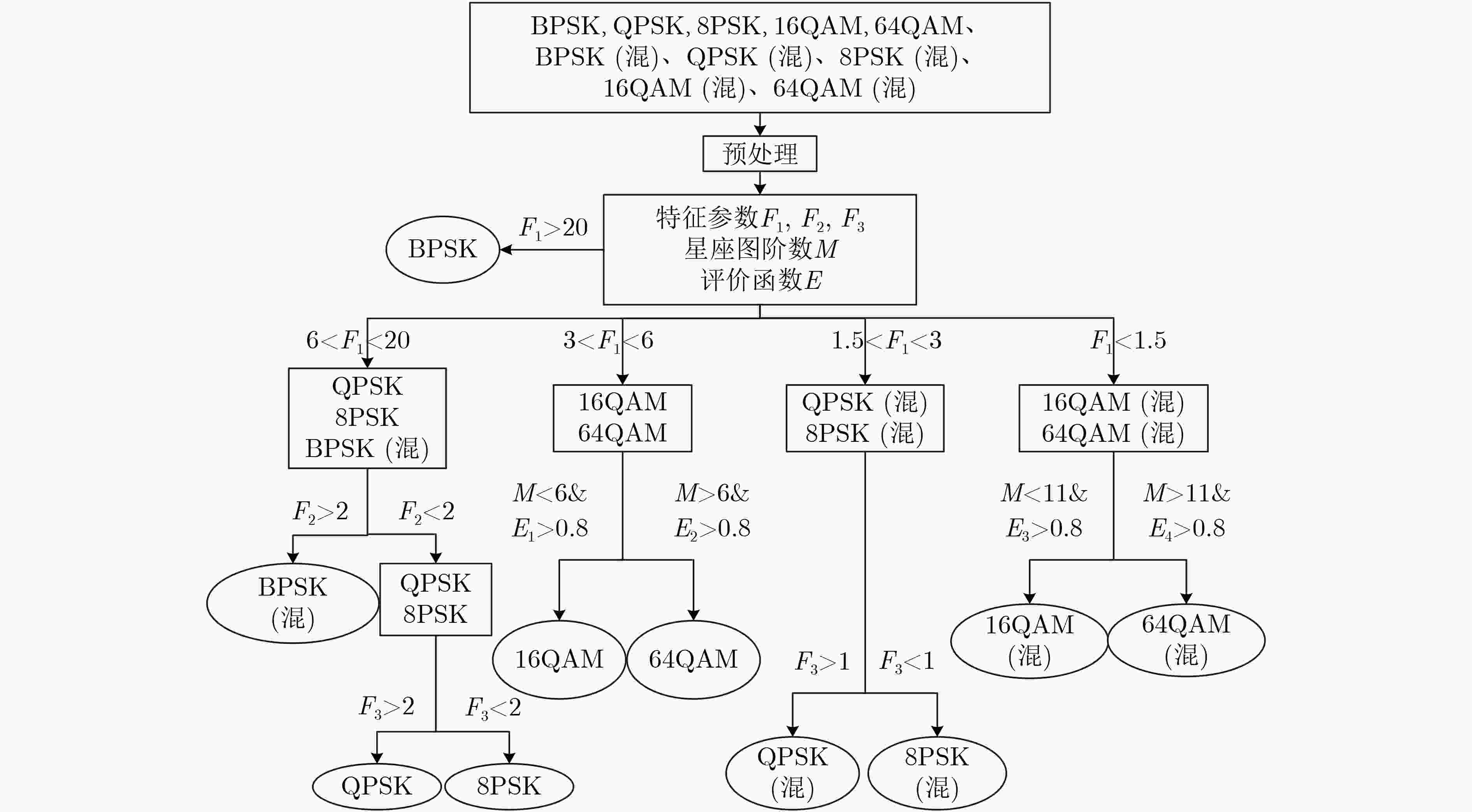
摘要: 针对卫星通信中单-混信号调制类型识别效率低、准确性差等问题,该文提出一种基于高阶累积量和星座图聚类特性的调制识别算法。首先,根据4, 6阶累积量的属性特点构建3个特征参数,以识别多进制相移键控(MPSK)和部分多进制正交幅度调制(MQAM)调制类型,然后结合改进的星座图减法聚类算法分离出剩余调制样式,最后将参数联合,建立决策树分类器进行统一调度。该算法不依赖信号诸多先验信息,具有特征提取参数简单、识别种类多等特点。仿真结果表明,该算法在信噪比(SNR)10 dB下对卫星单-混信号的调制识别率仍能达到90%以上。Abstract: In order to tackle the problem of single-mixed signal modulation type recognition with low efficiency and poor accuracy in satellite communication, based on clustering characteristics of constellation and high order cumulants, a joint algorithm is proposed. Firstly, three characteristic parameters is constructed with the utilization of the 4th and 6th order cumulants to identify Multiple Phase Shift Keying (MPSK) and partial Multiple Quadrature Amplitude Modulation (MQAM) modulation types, then the improved constellation subtraction clustering algorithm is combined to separate the remaining modulation patterns, At last, the parameters are integrated to establish a decision tree classifier for unified scheduling. By adopting the method of this article, many signals without prior knowledge are unnecessarily required, and meanwhile the proposed approach maintains the characteristics of simple feature extraction parameters and multiple recognition types. The simulation experiments demonstrate that the associated algorithm is still able to achieve the validity of more than 90%, in the circumstance of the satellite single-mixed signals possessing a Signal-to-Noise Ratio (SNR) of 10 dB.
-
表 1 单-混信号高阶累积量理论值
调制类型 ${C_{20}}$ ${C_{21}}$ ${C_{40}}$ ${C_{41}}$ ${C_{42}}$ ${C_{60}}$ ${C_{63}}$ BPSK $E$ $E$ $ - 2{E^2}$ $ - 2{E^2}$ $ - 2{E^2}$ $16{E^3}$ $16{E^3}$ QPSK $0$ $E$ ${E^2}$ $0$ $ - {E^2}$ $0$ $4{E^3}$ 8PSK $0$ $E$ $0$ $0$ $ - {E^2}$ $0$ $4{E^3}$ 16QAM $0$ $E$ $ - 0.68{E^2}$ $0$ $ - 0.68{E^2}$ $0$ $2.08{E^3}$ 64QAM $0$ $E$ ${{\rm{ - }}}0.6191{E^2}$ $0$ ${{\rm{ - }}}0.6191{E^2}$ $0$ $1.7972{E^3}$ BPSK混 $E$ $E$ ${{\rm{ - }}}{E^2}$ $ - {E^2}$ $ - {E^2}$ $4{E^3}$ $4{E^3}$ QPSK混 $0$ $E$ ${{\rm{ - }}}0.5{E^2}$ $0$ $ - 0.5{E^2}$ $0$ ${E^3}$ 8PSK混 $0$ $E$ $0$ $0$ $ - 0.5{E^2}$ $0$ ${E^3}$ 16QAM混 $0$ $E$ $ - 0.34{E^2}$ $0$ $ - 0.34{E^2}$ $0$ $0.52{E^3}$ 64QAM混 $0$ $E$ ${{\rm{ - }}}0.3096{E^2}$ $0$ ${{\rm{ - 0}}}{{\rm{.3096}}}{E^2}$ $0$ $0.4493{E^3}$ 表 2 MQAM单混调制信号聚类中心及相关系数
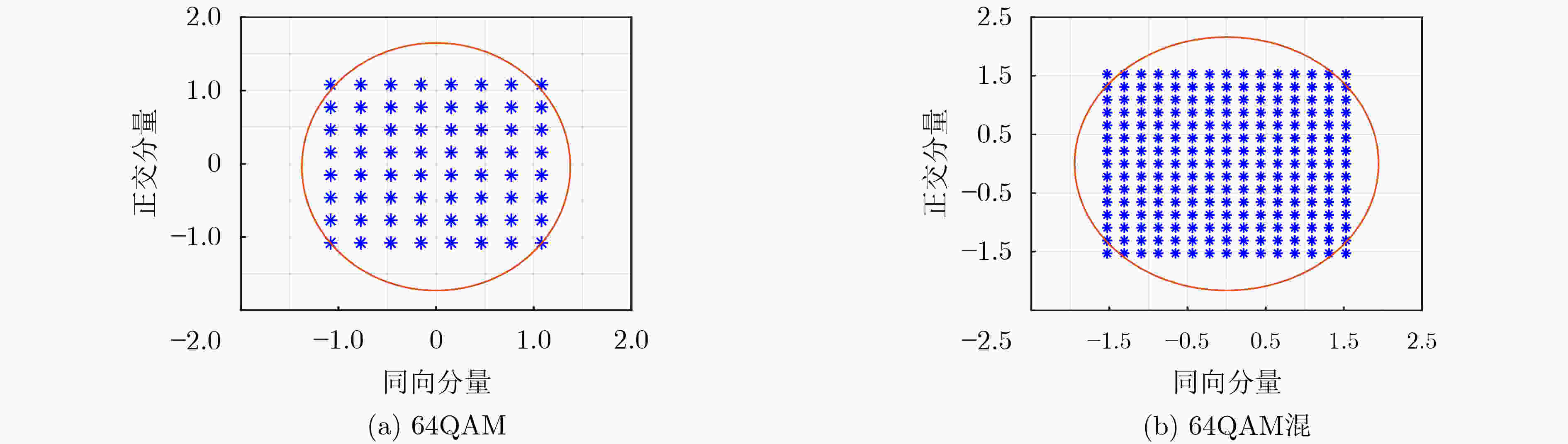
调制类型 密度半径${r_a}$ 判决系数$\lambda $ 聚类中心数${N_s}$ 16QAM 0.63 0.100 16 64QAM 0.38 0.100 64 16QAM混 0.35 0.010 49 64QAM混 0.22 0.001 225 表 3 MQAM信号的
${{\boldsymbol{r}}_{{\bf{max}} }}$ ,${{\boldsymbol{r}}_{{\bf{min}} }}$ ,${{\boldsymbol{R}}_{\boldsymbol{s}}}$ 理论值调制类型 最大半径${r_{\max }}$ 最小半径${r_{\min }}$ 标准半径${R_s}$ 16QAM ${3 \mathord{\left/{\vphantom {3 {\sqrt 5 }}} \right.} {\sqrt 5 }}$ $ {1 \mathord{\left/{\vphantom {1 {\sqrt 5 }}} \right.} {\sqrt 5 }} $ $3$ 64QAM ${7 \mathord{\left/{\vphantom {7 {\sqrt {21} }}} \right.} {\sqrt {21} }}$ ${1 \mathord{\left/{\vphantom {1 {\sqrt {21} }}} \right.} {\sqrt {21} }}$ $7$ 16QAM混 ${6 \mathord{\left/{\vphantom {6 {\sqrt {10} }}} \right.} {\sqrt {10} }}$ ${1 \mathord{\left/{\vphantom {1 {\sqrt {10} }}} \right.} {\sqrt {10} }}$ $6$ 64QAM混 ${{14} \mathord{\left/{\vphantom {{14} {\sqrt {42} }}} \right.} {\sqrt {42} }}$ ${1 \mathord{\left/{\vphantom {1 {\sqrt {42} }}} \right.} {\sqrt {42} }}$ $14$ 表 4 MQAM信号的
${{\boldsymbol{r}}_{{\bf{min}} }}$ ,${{\boldsymbol{R}}_{\boldsymbol{s}}}$ ,${{\boldsymbol{N}}_{\boldsymbol{s}}}$ 理论值调制类型 最小半径${r_{\min }}$ 标准半径${R_s}$ 聚类中心数${N_s}$ 16QAM $ {{\sqrt 2 } \mathord{\left/{\vphantom {{\sqrt 2 } {\sqrt 5 }}} \right.} {\sqrt 5 }} $ 3 4 64QAM ${{\sqrt 2 } \mathord{\left/{\vphantom {{\sqrt 2 } {\sqrt {21} }}} \right.} {\sqrt {21} }}$ 7 8 16QAM混 ${1 \mathord{\left/{\vphantom {1 {\sqrt 5 }}} \right.} {\sqrt 5 }}$ 6 7 64QAM混 $ {1 \mathord{\left/{\vphantom {1 {\sqrt {21} }}} \right.} {\sqrt {21} }} $ 14 15 表 5 星座图聚类算法下的MQAM信号识别率(%)
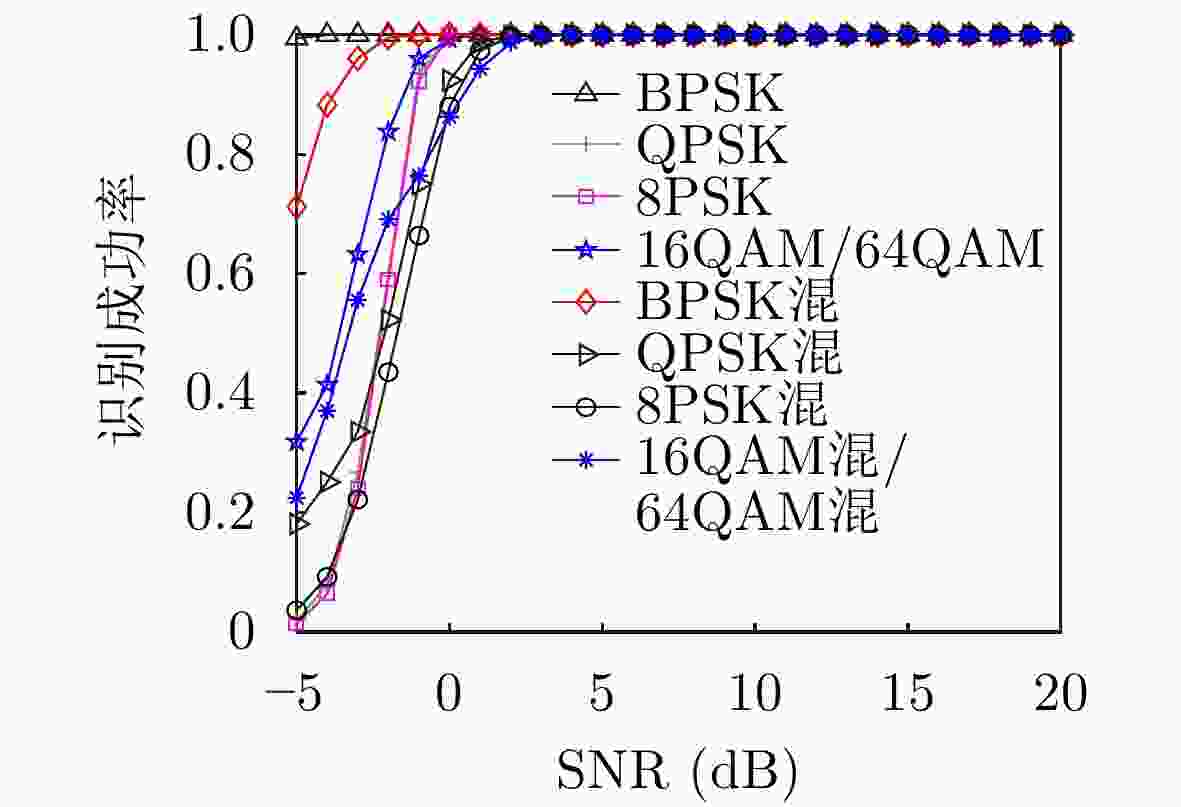
调制类型 MQAM(单)类型识别率 SNR=5 dB SNR=10 dB SNR=15 dB SNR=20 dB 16QAM 64QAM 16QAM 64QAM 16QAM 64QAM 16QAM 64QAM 16QAM 91 9 99 1 100 0 100 0 64QAM 15 85 4 94 2 98 0 100 调制类型 MQAM(混)类型识别率 SNR=5 dB SNR=10 dB SNR=15 dB SNR=20 dB 16QAM混 64QAM混 16QAM混 64QAM混 16QAM混 64QAM混 16QAM混 64QAM混 16QAM混 12 88 95 5 100 0 100 0 64QAM混 25 75 10 90 5 95 3 97 -
[1] 张天骐, 范聪聪, 葛宛营, 等. 基于ICA和特征提取的MIMO信号调制识别算法[J]. 电子与信息学报, 2020, 42(9): 2208–2215. doi: 10.11999/JEIT190320ZHANG Tianqi, FAN Congcong, GE Wanying, et al. MIMO signal modulation recognition algorithm based on ICA and feature extraction[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2208–2215. doi: 10.11999/JEIT190320 [2] WANG Tuo, HOU Yonghong, ZHANG Haoyuan, et al. Deep learning based modulation recognition with multi-cue fusion[J]. IEEE Wireless Communications Letters, 2021, 10(8): 1757–1760. doi: 10.1109/LWC.2021.3078878 [3] DANKBERG M. Paired carrier multiple access (PCMA) for satellite communications[C]. 17th AIAA International Communications Satellite Systems Conference and Exhibit, Yokohama, Japan, 1998: 787–791. [4] LUO Zhongqiang, ZHU Lidong, LI Chengjie, et al. Blind extraction for PCMA downlink mixed signals using guided signature[C]. 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 2018: 1218–1222. doi: 10.1109/CompComm.2018.8780845. [5] 廖灿辉, 万坚, 周世东. 利用累积量和似然特征的卫星单-混信号调制识别算法[J]. 电讯技术, 2010, 50(7): 44–48. doi: 10.3969/j.issn.1001-893x.2010.07.010LIAO Canhui, WAN Jian, and ZHOU Shidong. Modulation classification algorithm for satellite single-mixed signals using cumulants and likehood features[J]. Telecommunication Engineering, 2010, 50(7): 44–48. doi: 10.3969/j.issn.1001-893x.2010.07.010 [6] 彭闯, 杨晓静, 蔡晓霞. 卫星单-混信号识别研究[J]. 火力与指挥控制, 2019, 44(8): 29–33, 40.PENG Chuang, YANG Xiaojing, and CAI Xiaoxia. Research on identification of satellite single-mixed signals[J]. Fire Control &Command Control, 2019, 44(8): 29–33, 40. [7] 贾子欣, 陈卫东, 杨松. PCMA信号调制识别研究[J]. 电子测量技术, 2020, 43(20): 133–138.JIA Zixin, CHEN Weidong, and YANG Song. Research on PCMA signal modulation recognition[J]. Electronic Measurement Technology, 2020, 43(20): 133–138. [8] ZENG Yuan, ZHANG Meng, HAN Fei, et al. Spectrum analysis and convolutional neural network for automatic modulation recognition[J]. IEEE Wireless Communications Letters, 2019, 8(3): 929–932. doi: 10.1109/LWC.2019.2900247 [9] HONG Dehua, ZHANG Zilong, and XU Xiaodong. Automatic modulation classification using recurrent neural networks[C]. 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 2017: 695–700. doi: 10.1109/CompComm.2017.8322633. [10] ZHANG Duona, DING Wenrui, ZHANG Baochang, et al. Automatic modulation classification based on deep learning for unmanned aerial vehicles[J]. Sensors, 2018, 18(3): 924. doi: 10.3390/s18030924 [11] NURSIAGA R and ALAYDRUS M. Efficiency of satellite transponder using paired carrier multiple access with low density parity check[C]. 2019 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET), Tangerang, Indonesia, 2019: 109–112. doi: 10.1109/ICRAMET47453.2019.8980423. [12] SWAMI A and SADLER B M. Hierarchical digital modulation classification using cumulants[J]. IEEE Transactions on Communications, 2000, 48(3): 416–429. doi: 10.1109/26.837045 [13] LIU Qianyu, KWONG C F, ZHANG Sibo, et al. A fuzzy-clustering based approach for MADM handover in 5G ultra-dense networks[J]. Wireless Networks, 2022, 28(2): 965–978. doi: 10.1007/s11276-019-02130-3. [14] JAJOO G, KUMAR Y, and YADAV S K. Blind signal PSK/QAM recognition using clustering analysis of constellation signature in flat fading channel[J]. IEEE Communications Letters, 2019, 23(10): 1853–1856. doi: 10.1109/LCOMM.2019.2929127 [15] ASLAM M W, ZHU Zhechen, and NANDI A K. Automatic modulation classification using combination of genetic programming and KNN[J]. IEEE Transactions on Wireless Communications, 2012, 11(8): 2742–2750. doi: 10.1109/TWC.2012.060412.110460 -





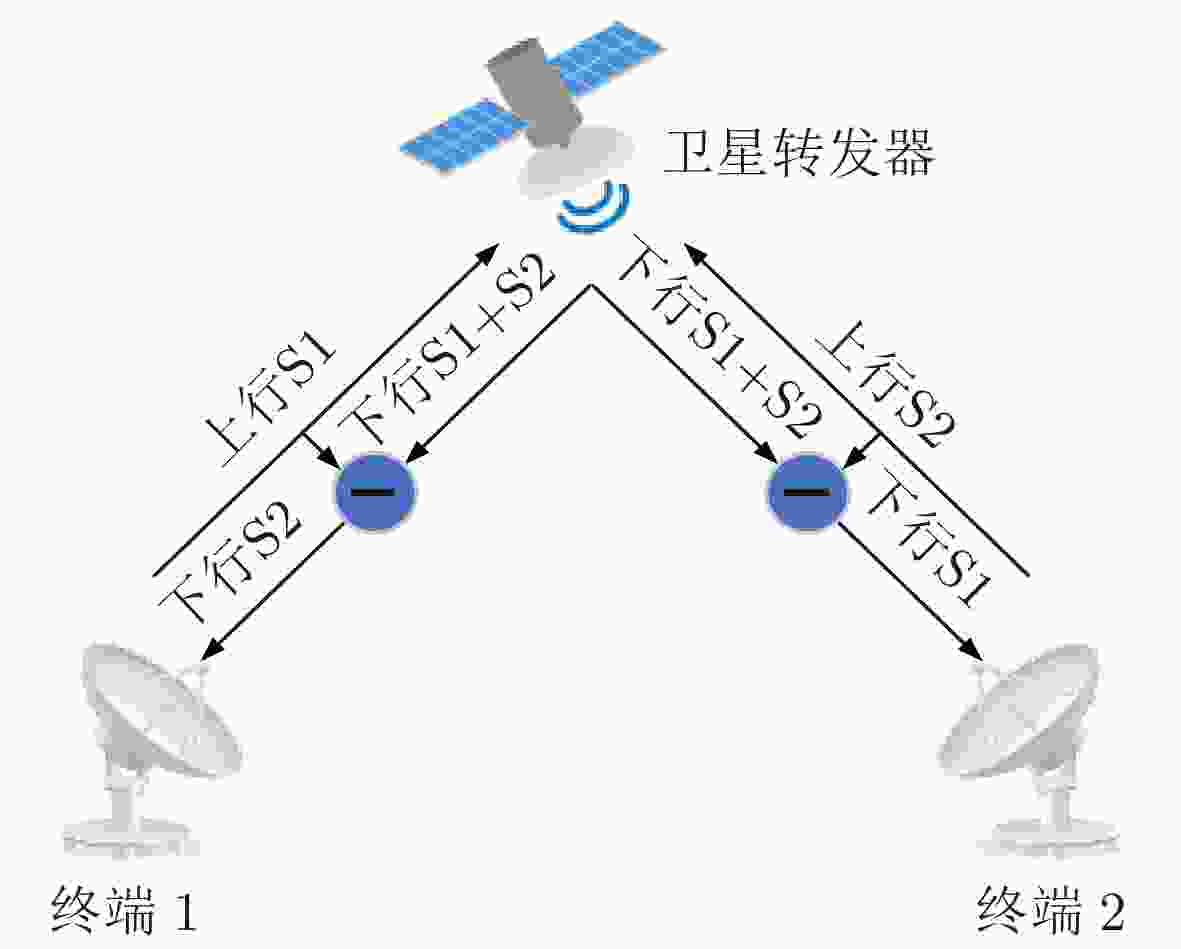
 下载:
下载:
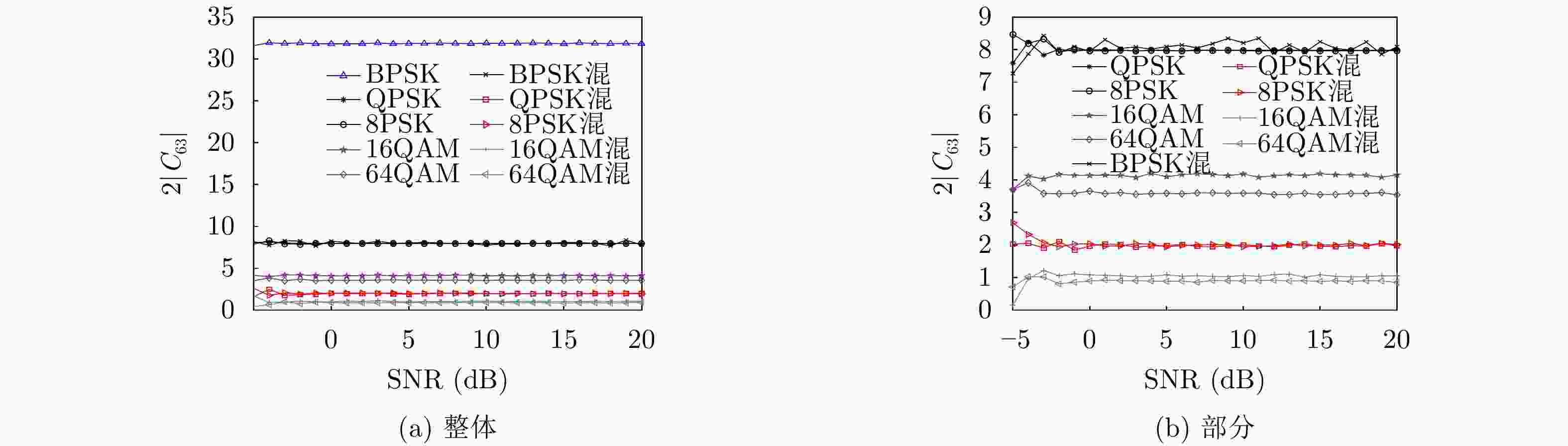

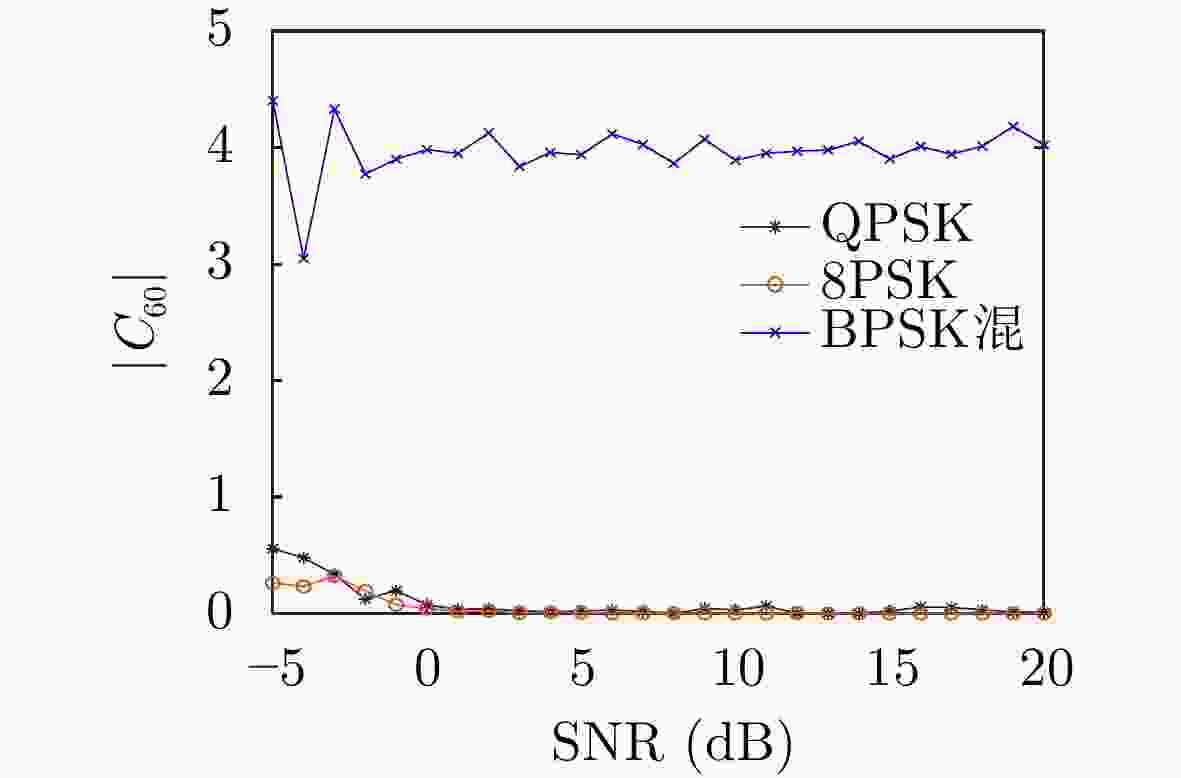



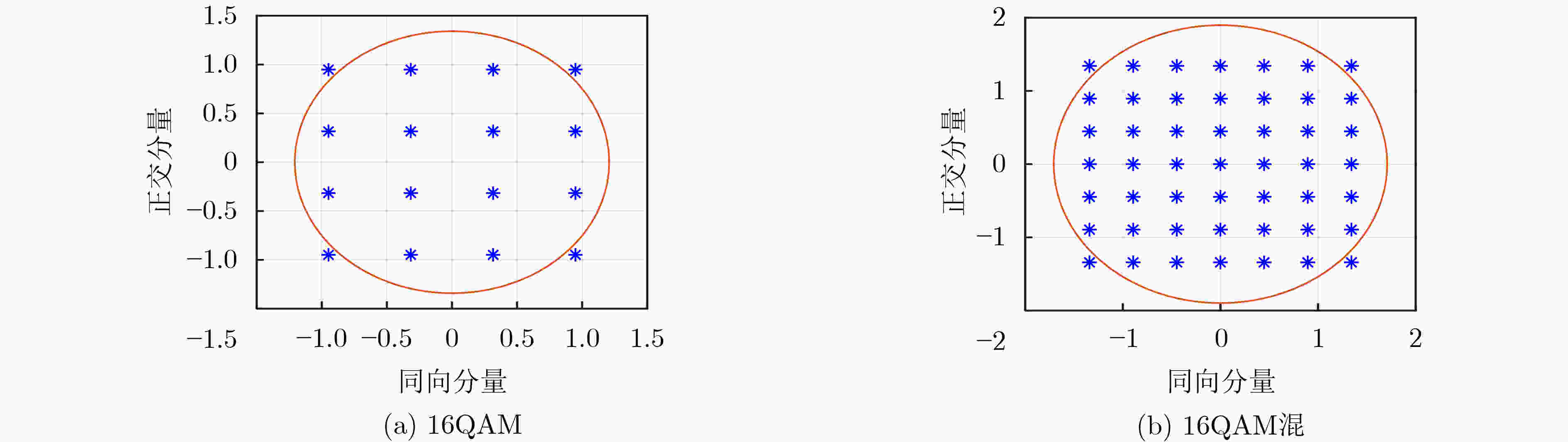








 下载:
下载:
