Multi-Modal Pulmonary Mass Segmentation Network Based on Cross-Modal Spatial Alignment
-
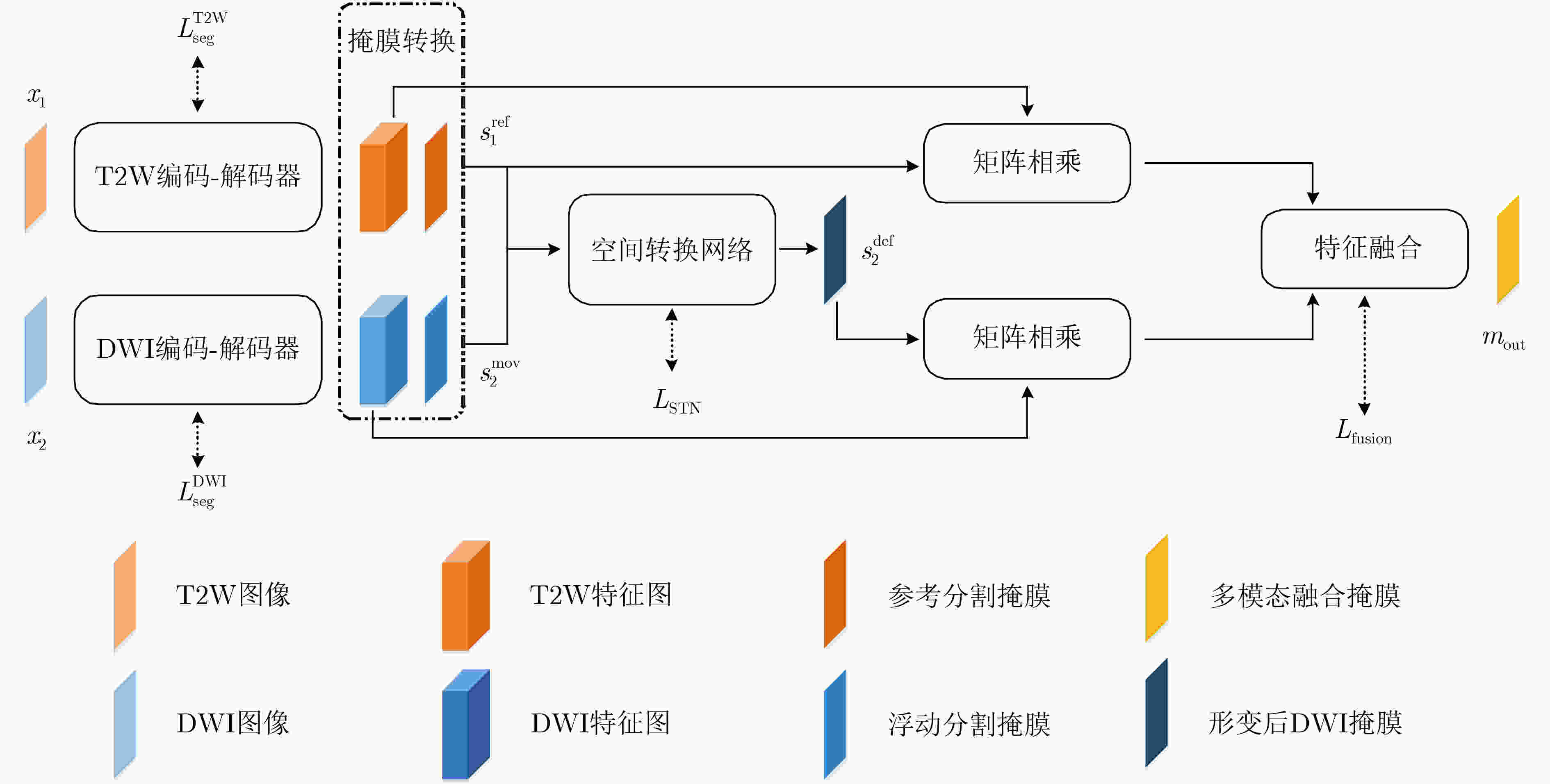
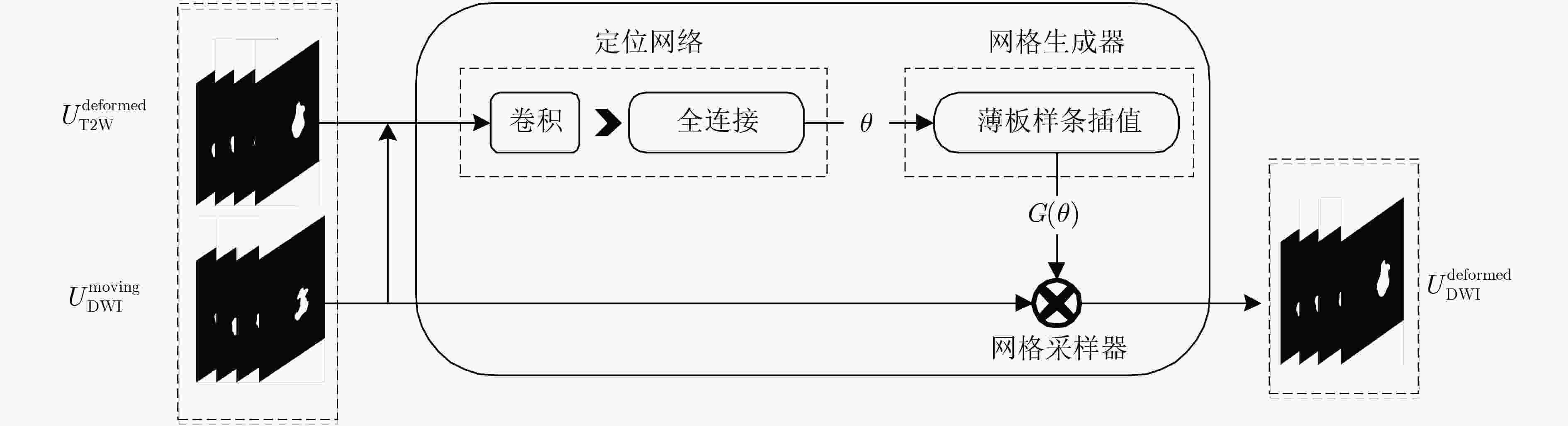
摘要: 现有多模态分割方法通常先对图像进行配准,再对配准后的图像进行分割。对于成像特点差异较大的不同模态,两阶段的结构匹配与分割算法下的分割精度较低。针对该问题,该文提出一种基于跨模态空间匹配的多模态肺部肿块分割网络(MMSASegNet),其具有模型复杂度低和分割精度高的特点。该模型采用双路残差U型分割网络作为骨干分割网络,以充分提取不同模态输入特征,利用可学习的空间变换网络对其输出的多模态分割掩膜进行空间结构匹配;为实现空间匹配后的多模态特征图融合,形变掩膜和参考掩膜分别与各自模态相同分辨率的特征图进行矩阵相乘,并经特征融合模块,最终实现多模态肺部肿块分割。为提高端到端多模态分割网络的分割性能,采用深度监督学习策略,联合损失函数约束肿块分割、肿块空间匹配和特征融合模块,同时采用多阶段训练以提高不同功能模块的训练效率。实验数据采用T2权重(T2W)磁共振图像和扩散权重磁共振图像(DWI)肺部肿块分割数据集,该方法与其他多模态分割网络相比,DSC (Dice Similarity Coefficient)和HD (Hausdorff Distance)等评价指标均显著提高。Abstract: Most of the existing multi-modal segmentation methods are adopted on the co-registered multi-modal images. However, these two-stage algorithms of the segmentation and the registration achieve low segmentation performance on the modalities with remarkable spatial misalignment. To solve this problem, a cross-modal Spatial Alignment based Multi-Modal pulmonary mass Segmentation Network (MMSASegNet) with low model complexity and high segmentation accuracy is proposed. Dual-path Res-UNet is adopted as the backbone segmentation architecture of the proposed network for the better multi-modal feature extraction. Spatial Transformer Networks (STN) is applied to the segmentation masks from two paths to align the spatial information of mass region. In order to realize the multi-modal feature fusion based on the spatial alignment on the region of mass, the deformed mask and the reference mask are matrix-multiplied by the feature maps of each modality respectively. Further, the yielding cross-modality spatially aligned feature maps from multiple modalities are fused and learned through the feature fusion module for the multi-modal mass segmentation. In order to improve the performance of the end-to-end multi-modal segmentation network, deep supervision learning strategy is employed with the joint cost function constraining mass segmentation, mass spatial alignment and feature fusion. Moreover, the multi-stage training strategy is adopted to improve the training efficiency of each module. On the pulmonary mass datasets containing T2-Weighted-MRI(T2W) and Diffusion-Weighted-MRI Images(DWI), the proposed method achieved improvement on the metrics of Dice Similarity Coefficient (DSC) and Hausdorff Distance (HD).
-
表 1 多阶段训练超参数设置
0~30期 30~50期 50~55期 55~100期 学习率 0.001 0.0001 0.0001 0.001 $ \alpha $ 0 0.6 0.5 0.5 $ \beta $ 1 1.5 0.5 0.5 表 2 消融实验在测试集的测试结果(即五折交叉验证结果的平均值)
Model DSC 精确度 灵敏度 HD95 (pixels) Dual-path Res-UNet 0.828(±0.096) 0.835 0.865 3.19 MMSASegNet 0.854(±0.074) 0.862 0.875 3.01 表 3 对比实验在测试集的测试结果(即五折交叉验证结果的平均值)
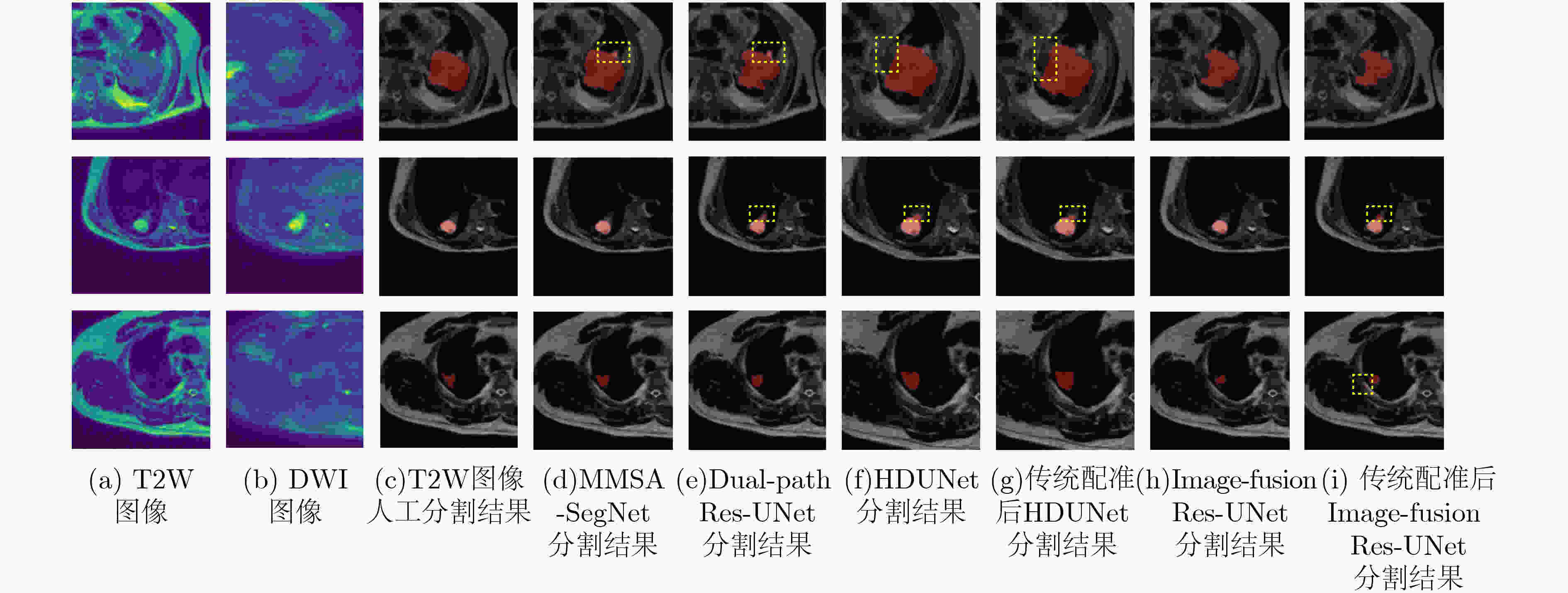
Model Params. DSC 精确度 灵敏度 HD95 (pixels) 训练时间(h) 测试时间(s) HDUNet [7] 24M 0.829(±0.110) 0.829 0.871 18.12 10 0.45 HDUNet [7] with registration — 0.817(±0.121) 0.792 0.892 18.93 — — Image-fusion Res-UNet [17] 33M 0.774(±0.142) 0.804 0.801 19.57 5 0.50 Image-fusion Res-UNet [17] with registration — 0.786(±0.135) 0.829 0.798 19.35 — — DAFNet [13] 52M 0.510(±0.207) 0.666 0.480 27.43 14 0.05 MMSASegNet 52M 0.854(±0.074) 0.862 0.875 3.01 7 0.04 -
[1] ALAM F and RAHMAN S U. Challenges and solutions in multimodal medical image subregion detection and registration[J]. Journal of Medical Imaging and Radiation Sciences, 2019, 50(1): 24–30. doi: 10.1016/j.jmir.2018.06.001 [2] HASKINS G, KRUGER U, and YAN Pingkun. Deep learning in medical image registration: A survey[J]. Machine Vision and Applications, 2020, 31(1/2): 8. doi: 10.1007/s00138-020-01060-x [3] ONG E P, CHENG Jun, WONG D W K, et al. A robust outliers’ elimination scheme for multimodal retina image registration using constrained affine transformation[C]. The TENCON 2018 - 2018 IEEE Region 10 Conference, Jeju, Korea (South), 2018: 425–429. [4] WANG Xiaoyan, MAO Lizhao, HUANG Xiaojie, et al. Multimodal MR image registration using weakly supervised constrained affine network[J]. Journal of Modern Optics, 2021, 68(13): 679–688. doi: 10.1080/09500340.2021.1939897 [5] RUECKERT D, SONODA L I, HAYES C, et al. Nonrigid registration using free-form deformations: Application to breast MR images[J]. IEEE Transactions on Medical Imaging, 1999, 18(8): 712–721. doi: 10.1109/42.796284 [6] DOLZ J, GOPINATH K, YUAN Jing, et al. HyperDense-Net: A hyper-densely connected CNN for multi-modal image segmentation[J]. IEEE Transactions on Medical Imaging, 2019, 38(5): 1116–1126. doi: 10.1109/TMI.2018.2878669 [7] LI Jiaxin, CHEN Houjin, LI Yanfeng, et al. A novel network based on densely connected fully convolutional networks for segmentation of lung tumors on multi-modal MR images[C]. The 2019 International Conference on Artificial Intelligence and Advanced Manufacturing, Dublin, Ireland, 2019: 69. [8] CAI Naxin, CHEN Houjin, LI Yanfeng, et al. Adaptive weighting landmark-based group-wise registration on lung DCE-MRI images[J]. IEEE Transactions on Medical Imaging, 2021, 40(2): 673–687. doi: 10.1109/TMI.2020.3035292 [9] ZHU Wentao, MYRONENKO A, XU Ziyue, et al. NeurReg: Neural registration and its application to image segmentation[C]. 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass, USA, 2020: 3606–3615. [10] LIU Jie, XIE Hongzhi, ZHANG Shuyang, et al. Multi-sequence myocardium segmentation with cross-constrained shape and neural network-based initialization[J]. Computerized Medical Imaging and Graphics, 2019, 71: 49–57. doi: 10.1016/j.compmedimag.2018.11.001 [11] XU R S, ATHAVALE P, LU Yingli, et al. Myocardial segmentation in late-enhancement MR images via registration and propagation of cine contours[C]. The 10th International Symposium on Biomedical Imaging, San Francisco, USA, 2013: 856–859. [12] ZHUANG Xiahai. Multivariate mixture model for myocardial segmentation combining multi-source images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(12): 2933–2946. doi: 10.1109/TPAMI.2018.2869576 [13] CHARTSIAS A, PAPANASTASIOU G, WANG Chengjia, et al. Disentangle, align and fuse for multimodal and semi-supervised image segmentation[J]. IEEE Transactions on Medical Imaging, 2021, 40(3): 781–792. doi: 10.1109/TMI.2020.3036584 [14] JADERBERG M, SIMONYAN K, ZISSERMAN A, et al. Spatial transformer networks[C]. The 28th International Conference on Neural Information Processing Systems, Montreal, Canada, 2015: 2017–2025. [15] RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. The 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015. [16] LEE C Y, XIE Saining, GALLAGHER P W, et al. Deeply-supervised nets[C]. The 18th International Conference on Artificial Intelligence and Statistics (AISTATS), San Diego, USA, 2015. [17] KHANNA A, LONDHE N D, GUPTA S, et al. A deep Residual U-Net convolutional neural network for automated lung segmentation in computed tomography images[J]. Biocybernetics and Biomedical Engineering, 2020, 40(3): 1314–1327. doi: 10.1016/j.bbe.2020.07.007 -





 下载:
下载:


 下载:
下载:
