基于多智能体模糊深度强化学习的跳频组网智能抗干扰决策算法

赵知劲; 朱家晟; 叶学义; 尚俊娜

doi:10.11999/JEIT210608

基于多智能体模糊深度强化学习的跳频组网智能抗干扰决策算法

doi: 10.11999/JEIT210608

赵知劲^{1, 2},
朱家晟^2, ,,
叶学义²,
尚俊娜²

1.
中国电子科技集团第 36研究所通信系统信息控制技术国家级重点实验室嘉兴 314001
2.
杭州电子科技大学通信工程学院杭州 310018

基金项目: 国家自然科学基金(U19B2016)

详细信息

作者简介:
赵知劲：女，1959年生，博士，研究方向为认知无线电、通信信号处理和自适应信号处理等

朱家晟：男，1997年生，硕士生，研究方向为智能抗干扰决策

叶学义：男，1973年生，博士，研究方向为图像处理、模式识别、信息隐藏

尚俊娜：女，1979年生，博士，研究方向为通信信号处理、无线传感网络研究、卫星导航定位

通讯作者:
朱家晟　1045314503@qq.com

中图分类号: TN914; TN973
计量
- 文章访问数: 1729
- HTML全文浏览量: 873
- PDF下载量: 209
- 被引次数: 5
出版历程
- 收稿日期: 2021-06-21
- 修回日期: 2021-10-26
- 网络出版日期: 2021-11-13
- 刊出日期: 2022-08-17

Intelligent Anti-jamming Decision Algorithm for Frequency Hopping Network Based on Multi-agent Fuzzy Deep Reinforcemnet Learning

ZHAO Zhijin^{1, 2},
ZHU Jiasheng^{2
, ,},
YE Xueyi²,
SHANG Junna²

1.
State Key Laboratory of Information Control Technology in Communication System of No.36 Research Institute, China Electronic Technology Corporation, Jiaxing 314001, China
2.
School of Communication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China

Funds: The National Natural Science Foundation of China (U19B2016)

摘要

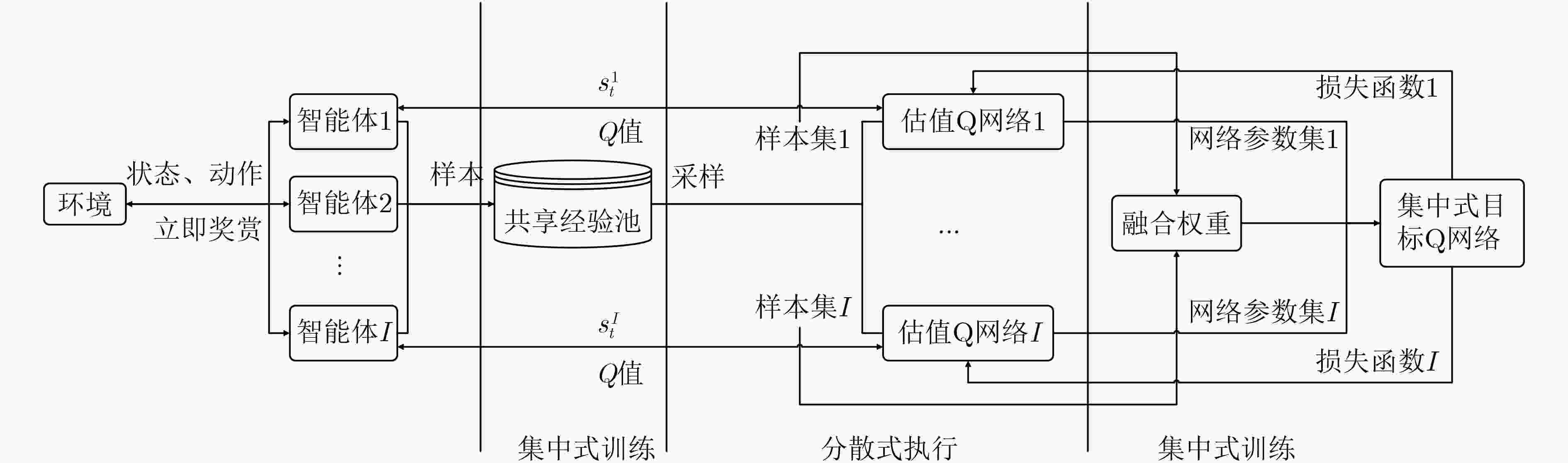
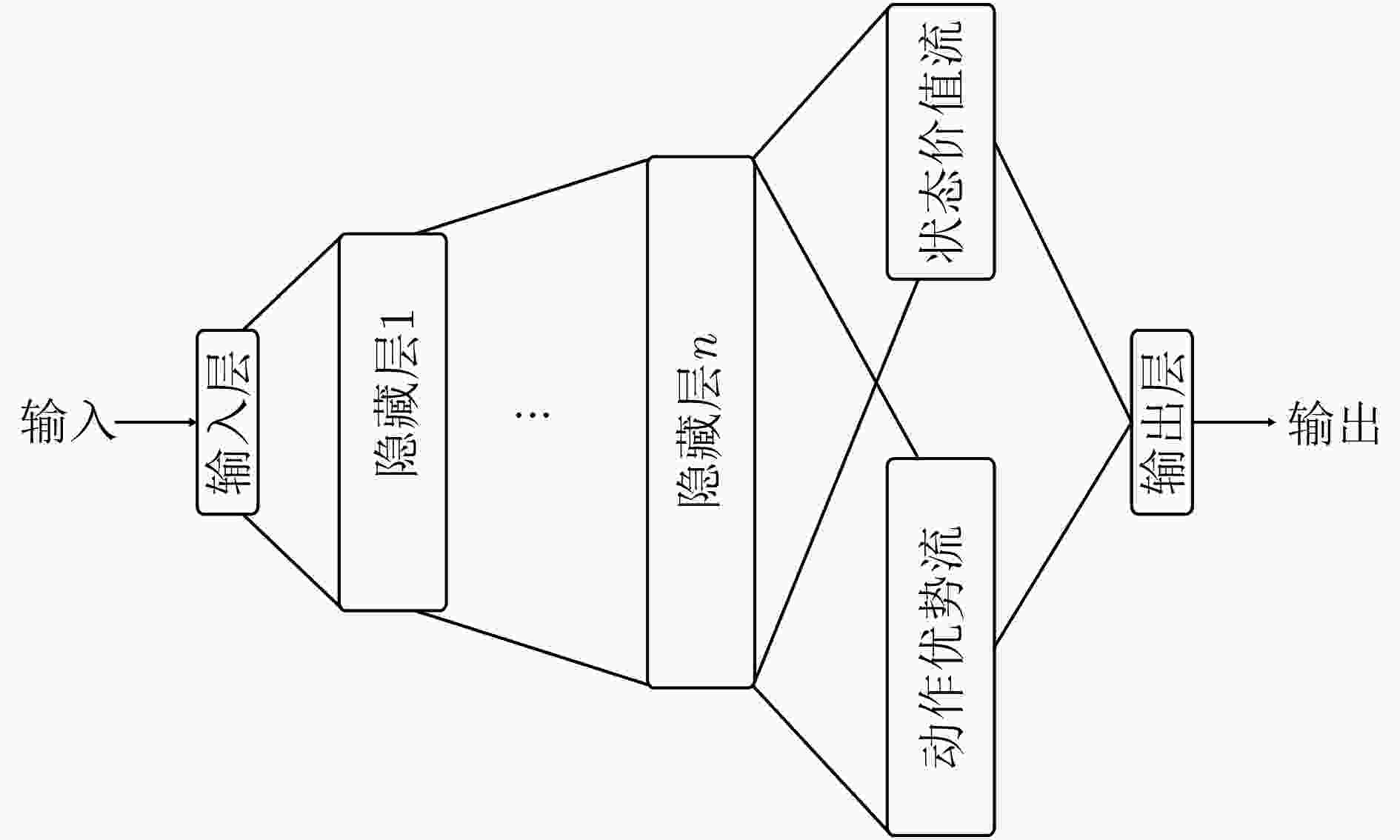
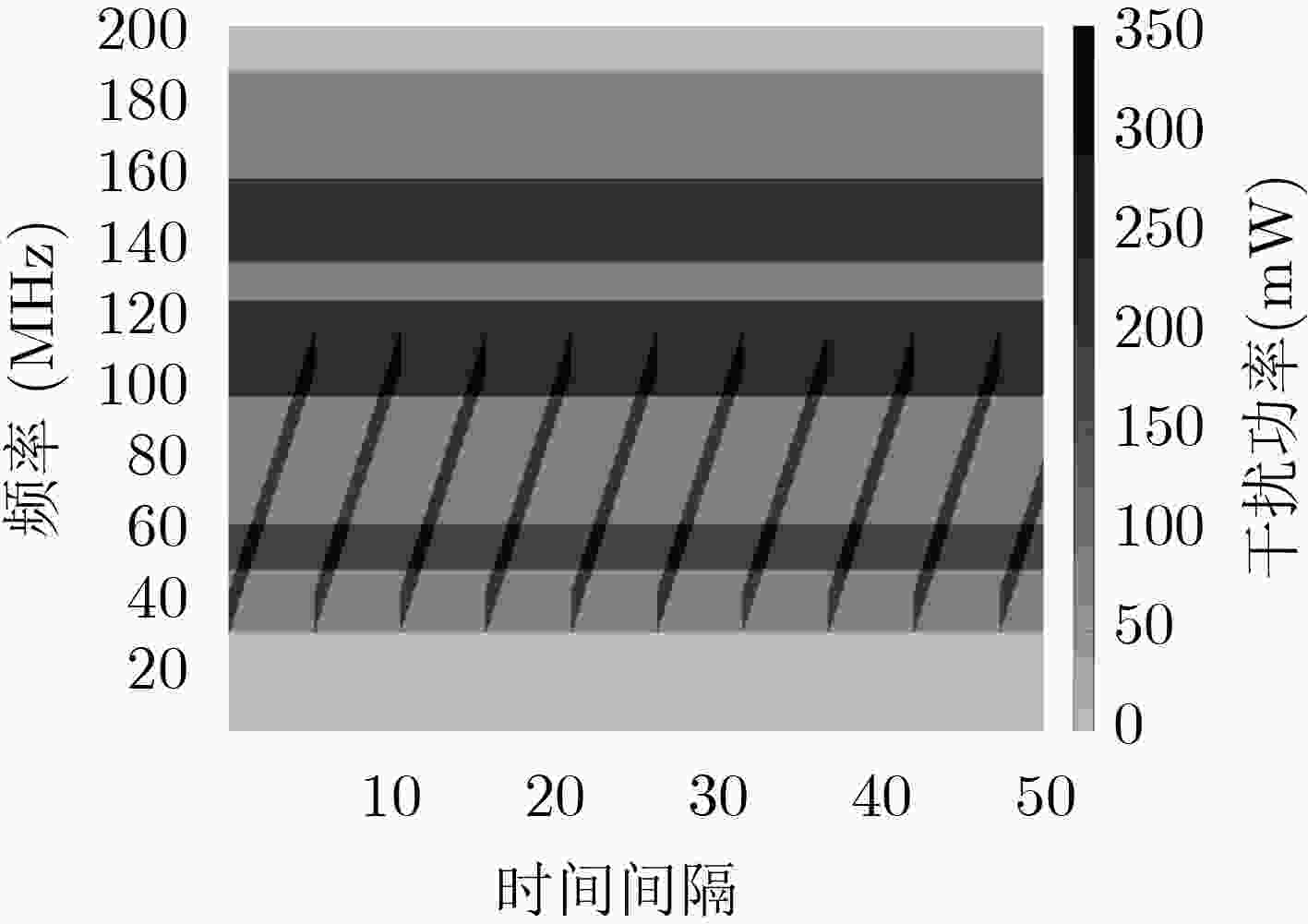
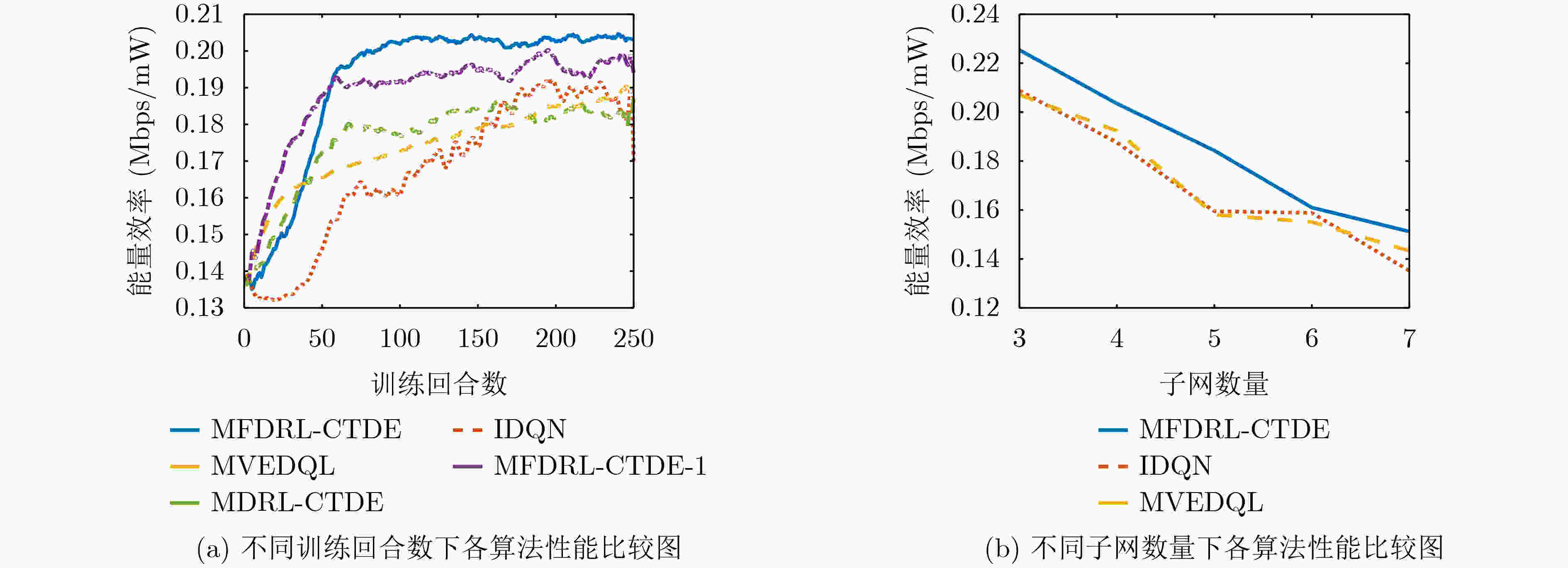
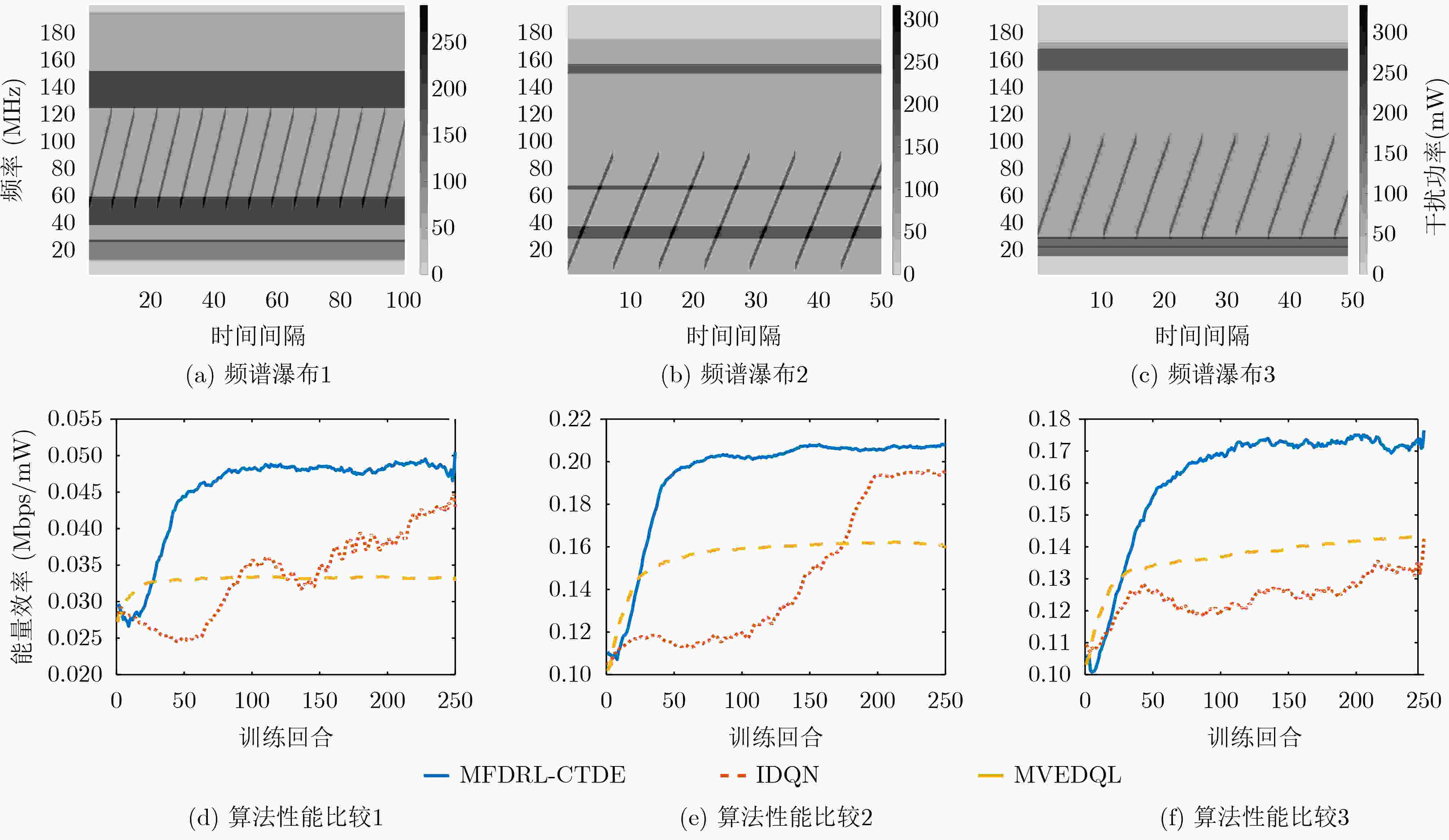
摘要: 为提高复杂电磁环境下跳频异步组网的抗干扰性能，该文提出一种基于集中式训练和分散式执行框架的多智能体模糊深度强化学习(MFDRL-CTDE)算法。针对多种干扰并存的复杂电磁环境和异步组网结构，设计了相应的状态-动作空间和奖赏函数。为应对智能体之间的相互影响和动态的环境，引入集中式训练和分散式执行(CTDE)框架。该文提出基于模糊推理系统的融合权重分配策略，用于解决网络融合过程中各智能体的权重分配问题。采用竞争性深度Q网络算法和优先经验回放技术以提高算法的效率。仿真结果表明，该算法在收敛速度和最佳性能方面都具有较大优势，且对多变复杂电磁环境具有较好的适应性。
- 异步组网 /
- 多智能体 /
- 深度强化学习 /
- 集中式学习和分散式执行 /
- 模糊推理系统
Abstract: In order to improve the anti-jamming performance of frequency hopping asynchronous network in complex electromagnetic environment, a Multi-agent Fuzzy Deep Reinforcement Learning algorithm based on Centralized Training and Decentralized Execution (MFDRL-CTDE) is proposed. Considering the complex electromagnetic environment with multiple interferences and the asynchronous network structure, the corresponding state-action space and reward function are designed. For dealing with the interaction between agents and the dynamic environment, the framework of Centralized Training and Decentralized Execution (CTDE) is introduced. Then, a fusion weight allocation strategy based on fuzzy inference system is proposed to solve the weight allocation problem in the process of network fusion. And the Dueling DQN algorithm and the prioritized experience replay technology are used to improve the efficiency of the algorithm. The simulation results show that the algorithm has a great advantage in convergence speed and best performance, and has good adaptability to the changeable complex electromagnetic environment.
- Asynchronous network /
- Multi agent /
- Deep reinforcement learning /
- Centralized Training with Decentralized Execution (CTDE) /
- Fuzzy inference system

HTML全文

1. 引言

近几年来，国内外有大量的学者在研究近场源定位问题，提出了许多方法^[1–7]，比如文献[1]的最大似然估计法，文献[2～4]的MUSIC算法，文献[5,6]的基于高阶累积量的算法，文献[7]的基于圆阵的相位差封闭式算法。这些方法大多是针对等距均匀阵列提出的，而且在研究过程中很少考虑到误差导致定位算法性能下降甚至是失效的问题。

针对幅相不一致误差校正的问题，一些方法相继被提出来，比如文献[8]提出利用独立分析法进行盲校正的方法，但是针对非高斯信号的幅相误差，文献[9]利用稀疏矩阵实现方位与误差的联合估计，缺点是幅相误差、互耦误差等各种误差混在一起，没有分离开。随着对近场源定位研究不断深入，对其幅相误差的校正成为越来越重要的问题。当前，对近场源幅相误差校正方法分为3类：一是将远场信号幅相误差校正方法直接用于近场信号的幅相误差校正，如文献[10]采用的算法，属于自校正^[10–12]，但在近场条件下距离与方位是耦合的导致不能直接在近场条件下使用；二是利用远近场混合信号的误差校正方法，如文献[13]对远近场混合信号进行幅相误差校正，远场信源作为辅助信号，利用远场信号先验知识对幅相误差校正后对近场信号进行估计，无需谱峰搜索，但需借助远场信号，是有源校正^[13,14]，这类算法本质上是远场校正方法的运用，在空间受限的近场条件下无法使用；三是采用直接用于近场源幅相误差校正的方法，文献[15]是通过迭代对阵列的幅相误差进行校正，利用改进2维MUSIC算法对近场源进行定位，但计算量大，且迭代对误差进行校正时容易产生偏差。

总地来说，直接利用近场源来校正近场的幅相误差的研究比较少，其难点在于误差、方位和距离之间均存在耦合，相比远场只存在方位与误差之间耦合的情况其复杂度增加不少。针对这一难点，本文提出采用均匀对称阵列以及辅助阵元，通过重构虚拟阵列实现方位、误差与距离之间的分离；再通过对虚拟阵列导向矢量的变换，实现了方位参数与误差之间的解耦合；在此基础上，通过变换实现距离与误差之间的解耦合。算法将原本需要误差、方位和距离等多维参数联合估计的问题，转化为对近场源的方位角、距离以及阵列的误差系数级联估计的问题，运算过程只需2次1维谱搜索，从而极大地降低了算法的运算量，同时算法对角度及距离参数的估计精确，且误差校正精度高。最后，通过仿真实验证明了算法的有效性。

2. 近场源阵列幅相误差的信号模型

2.1 阵列模型

本文采用以中心阵元为参考点的等距均匀对称阵列，阵元数为 $2M + 1$ ，如图1中“ $\bullet$ ”所示，阵元位置以 $d$ 为单位， $d$ 一般取 $\lambda /4$ ( $\lambda$ 为波长)。在上述对称阵列的两侧各增加 $P$ 个辅助阵元，如图1中“■”所示，组成的 $2K + 1 = 2P + 2M + 1$ 元等距对称线阵从辅助阵元开始编号，位置矢量为 $[{m_{ - K}} ·\!·\!· {m_{ - M - 1}}\;{m_{ - M}} ·\!·\!· {m_0} ·\!·\!· {m_M}\;{m_{M + 1}} ·\!·\!· {m_K}]d$ ，其中 ${m_m}$ 均为整数，且 $\ {m_0}$ 为 $\ 0$ 。

图 1 近场源的辅助阵元均匀对称阵列

下载: 全尺寸图片幻灯片

假设，有 $N$ $\left( {N < M + 1} \right)$ 个相互独立的零均值、平稳高斯的近场窄带信号源入射到如图1所示的等距均匀对称阵列上，则阵元 $k$ 接收到的信号表示为

${x_k}(t) = \sum\limits_{n = 1}^N {{s_n}(t){{\rm{e^{j{\tau _{kn}}}}}} + {n_k}(t),\;\;\;\;\; - K \le k} \le K$

(1)

式中， ${s_n}(t)$ 为第 $n$ 个信源， ${n_k}(t)$ 为零均值的加性白噪声，与信源相互独立， ${\tau _{kn}}$ 表示第 $n$ 个信源在第 $k$ 个阵元与参考阵元间因时延引起的相位差。近场源的 ${\tau _{kn}}$ 可由菲涅尔近似表示为

$\begin{align}{\tau _{kn}} =& \frac{{2{{π}} {r_n}}}{\lambda }\left( {\sqrt {1 + \frac{{m_k^2{d^2}}}{{r_n^2}} - \frac{{2{m_k}d \sin{\theta _n}}}{{{r_n}}}} - 1} \right)\\ \approx& {\mu _n}{m_k} + {\varphi _n}m_k^2\end{align}$

(2)

${\mu _n} = - 2{{π}} \frac{d}{\lambda } \sin{\theta _n},\;\;{\varphi _n} = {{π}} \frac{{{d^2}}}{{\lambda {r_n}}}{{\rm cos}^2}{\theta _n}$

(3)

式中， ${\theta _n} \in \left( { - \displaystyle\frac{{{π}} }{2},\displaystyle\frac{{{π}} }{2}} \right)$ 为第 $n$ 个信源与法线 $y$ 轴之间的夹角， ${r_n}$ 为第 $n$ 个信源与参考阵元之间的距离。因此式(1)可写为

$\begin{align}{x_k}(t) =& \sum\limits_{n = 1}^N {{s_n}(t){{\rm{e^{j\left( {{\mu _n}{m_k} + {\varphi _n}m_k^2} \right)}}}} + {n_k}(t),} \\ &- K \le k \le K\end{align}$

(4)

因此，整个阵列接收数据矢量为

${X}(t) = {AS}(t) + {N}(t)$

(5)

式中， ${X}(t)$ 为 $\left( {2K + 1} \right) \times 1$ 维快拍数据， ${N}(t)$ 为 $\left( {2K + 1} \right) \times 1$ 维噪声矢量， ${S}(t)$ 为 $N \times 1$ 维信号矢量， ${A}$ 为 $\left( {2K + 1} \right) \times N$ 维阵列流型。

${X}(t) = {\left[ {{x_{ - K}}(t)\; ·\!·\!·\;{x_0}(t)\; ·\!·\!· \;{x_K}(t)} \right]^\rm{T}}$

(6a)

${S}(t) = {\left[ {{s_1}(t)\;{s_2}(t) ·\!·\!· \;{s_N}(t)} \right]^\rm{T}}$

(6b)

${N}(t) = {[{n_{ - K}}(t) ·\!·\!· \;{n_0}(t)\; ·\!·\!· \;{n_K}(t)]^\rm{T}}$

(6c)

${A} = \left[ {{a}({\theta _1},{r_1})\; ·\!·\!· \;{a}({\theta _n},{r_n})\; ·\!·\!·\;{a}({\theta _N},{r_N})} \right]$

(6d)

$\begin{array}{l}{a}({\theta _n},{r_n})\\ \!=\!\! {\left[\! {{{\rm{e^{j\left( {{\mu _n}{m_{ - k}} + {\varphi _n}m_{ - k}^2} \right)}}}} ·\!·\!· {\rm{e^{j\left( {{\mu _n}{m_0} + {\varphi _n}m_0^2} \right)}}} ·\!·\!· {\rm{e^{j\left( {{\mu _n}{m_k} + {\varphi _n}m_k^2} \right)}}}} \right]^\rm{T}}\\\! =\!\! {\left[ {{a}_1^{\rm{T}}({\theta _n},{r_n})\;\;{a}_2^{\rm{T}}({\theta _n},{r_n})\;\;{a}_3^{\rm{T}}({\theta _n},{r_n})} \!\right]^\rm{T}}\end{array}$

(6e)

式中， ${\left[ \bullet \right]^\rm{T}}$ 表示转置， $P \times 1$ 维矢量 ${{a}_1}({\theta _n},{r_n})$ 是由对称阵列左侧 $P$ 个精确校正的辅助阵元对应的元素组成，同时 ${{a}_2}({\theta _n},{r_n})$ 是 $(2M + 1) \times 1$ 维矢量，是由对称阵列对应的元素组成的， $P \times 1$ 维矢量 ${{a}_3}({\theta _n},{r_n})$ 是由对称阵列右侧 $P\,$ 个精确校正的辅助阵元对应的元素组成。

2.2 误差条件下的数据模型

当阵列存在阵元通道幅相误差时，阵列接收的快拍数据式(5)变为

$\tilde {X}(t) ={\ \,{ \tilde^ \!\!\!\!\!\; {A} }} {S}(t) + {N}(t) = {{Γ}} {AS}(t) + {N}(t)$

(7)

式中， $\tilde {A}$ 为阵元存在通道幅相误差时的阵列流型矩阵，表示为

$\begin{align} \tilde {A} =& \left[ {{{Γ}} {a}({\theta _1},{r_1})\; ·\!·\!· \;{{Γ}} {a}({\theta _n},{r_n})\; ·\!·\!· \;{{Γ}} {a}({\theta _N},{r_N})} \right] \\ =& \left[ {\tilde {a}({\theta _1},{r_1})\;·\!·\!· \;\tilde {a}({\theta _n},{r_n})\; ·\!·\!· \;\tilde {a}({\theta _N},{r_N})} \right] \end{align}$

(8)

由上面的假设可知，辅助阵元均匀对称地分布在阵列的两侧，且辅助阵元是精确校正阵元，故幅相扰动矩阵 ${{Γ}}$ 中辅助阵元对应的元素为1，即

$\begin{align}{{Γ}} =& \rm{diag}[{{{{1}}}_{1 \times {{P}}}}\;{\alpha _{ - {{M}}}}\; ·\!·\!· \;{\alpha _0}\; ·\!·\!· \;{\alpha _{{M}}}\;{{{1}}_{1 \times {{P}}}}]\\=& \rm{diag}\left[ {{{{1}}_{1 \times{{P}}}}\;\;\;\;{{\left[ {\rm{vecd}({{{Γ}}_1})} \right]}^T}\;\;{{{1}}_{1 \times {{P}}}}} \right]\end{align}$

(9)

其中， $\rm{vecd}( \bullet )$ 代表将矩阵对角线上的元素取出构成列矢量， $\rm{diag}\left( \bullet \right)$ 表示将行向量构成对角矩阵。式中， ${{{1}}_{1 \times P}}$ 是 $(1 \times P)$ 维的全1行向量， ${{{Γ}} _1}$ 是 $(2M + 1) \times (2M + 1)$ 维的对角矩阵，是由对称阵列阵元的扰动幅相误差组成。

对于均匀对称阵列，导向矢量中 $m_{ - k}^2 =$ $m_k^2\left(\! {1 \!\le\! k \!\le\! K{{，}\;\;{{且}}k{{为整数}} \right)\!$ ，故阵列的导向矢量为

$\begin{align} \tilde {a}({\theta _n},{r_n}) =& {\left[ {{\alpha _{ - K}}{{\rm{e^j}^\left( {{\mu _{{n}}}{{{m}}_{ - {{k}}}} + {\varphi _{{n}}}{{m}}_{ - {{k}}}^2} \right)}}\; ·\!·\!· \;{\alpha _0}{{\rm{e^j}^\left( {{\mu _{{n}}}{{{m}}_0} + {\varphi _{{n}}}{{m}}_0^2} \right)}}\; ·\!·\!· \;{\alpha _K}{{{\rm{e^j}}^\left( {{\mu _{{n}}}{{{m}}_{{k}}} + {\varphi _{{n}}}m_{{k}}^2} \right)}}} \right]^\rm{T}} \\ = & {\left[ {{\alpha _{ - K}}{{\rm{e^j}^\left( {{\mu _{{n}}}{{{m}}_{ - {{k}}}} + {\varphi _{{n}}}{{m}}_{{k}}^2} \right)}}\; ·\!·\!· \;{\alpha _0}{{{\rm{e^j}}^\left( {{\mu _{{n}}}{{{m}}_0} + {\varphi _{{n}}}m_0^2} \right)}}\; ·\!·\!· \;{\alpha _K}{{\rm{e^j}^\left( {{\mu _{{n}}}{{{m}}_{{k}}} + {\varphi _{{n}}}{{m}}_{{k}}^2} \right)}}} \right]^\rm{T}} \end{align}$

(10)

因此，得到存在幅相不一致误差时的阵列数据协方差矩阵 $\tilde {R}$ ：

$\tilde {R} = \rm{E}[\tilde {X}({{t}}){\tilde {X}^\rm{H}}({{t}})] = \tilde {A}{{R}_{{S}}}{\tilde {A}^\rm{H}} + {\sigma ^2}{I}$

(11)

式中， $\rm{E}[ \bullet ]$ 表示数据的统计平均， ${{R}_S} \!=\! \rm{E}[{S}(t){{S}^\rm{H}}(t)]$ 为信号协方差矩阵， ${\sigma ^2}$ 为噪声功率， ${I}$ 是 $\left( {2K + 1} \right)$ $\times \left( {2K + 1} \right)$ 维的单位矩阵。将阵列的协方差矩阵 $\tilde {R}$ 进行特征分解，得

$\tilde {R} = {\tilde {U}_S}{\tilde {{Λ}} _S}\tilde {U}_S^{\rm{H}} + {\tilde {U}_N}{\tilde {{Λ}} _N}\tilde {U}_N^\rm{H}$

(12)

其中， ${\tilde {{Λ}}_S}$ 为存在误差时大特征值组成的对角阵， ${\tilde {{Λ}}_N}$ 为存在误差时小特征值组成的对角阵， ${\tilde {U}_S}$ 为存在误差时大特值对应的信号子空间， ${\tilde {U}_N}$ 为存在误差时小特征值对应的噪声子空间。

3. 近场源幅相误差校正算法

3.1 近场源的DOA估计

近场源定位需估计方位、距离两个参数，但阵列存在幅相误差时，方位、距离和误差三者间是耦合的，即估计其中一个参数就必须知道其它2个参数。通常情况下联合估计才能解决这种耦合问题，但为提高近场源定位的实时性，必须实现方位、距离与误差之间的解耦合。

通过仔细分析式(11)，抽取如下数据构造一个列矢量为

$\begin{align}{{Y}} =& \left[ {\tilde{{R}}(1,K)} \right. ·\!·\!· \tilde{{R}}(i,K + 1 - i) ·\!·· \\&{\left. {\tilde{{R}}(M + 1 + P,M + 1 + P)} \right]^{\rm{T}}}\end{align}$

(13)

由于

$\begin{align}&\tilde{ R}(i,K + 1 - i) = {\alpha _{ - i}}\alpha _i^*{x_{ - i}}x_i^ * \\&= {\alpha _{ - i}}\alpha _i^*\left( {\sum\limits_{n = 1}^N {{s_n}(t){{\rm{e^{j}}^\left( {{\mu _n}{m_{ - i}} + {\varphi _n}m_i^2} \right)}} + {n_{ - i}}(t)} } \right)\\&\quad \cdot\left( {\sum\limits_{n = 1}^N {{s_n}(t){{\rm{e^{ - j}}^\left( {{\mu _n}{m_i} + {\varphi _n}m_i^2} \right)}} + {n_i}(t)} } \right)\\& = {\alpha _{ - i}}\alpha _i^*{{\rm{e}}^{2{\rm{j}}{\mu _n}{m_{ - i}}}}{\left( {\sum\limits_{n = 1}^N {{s_n}(t)} } \right)^2}\end{align}$

(14)

将式(14)和式(5)对比发现，式(14)可看成是一个虚拟的等距均匀阵列，对于这个重构的虚拟阵列，存在 $P$ 个精确校正的辅助阵元和 $M + 1$ 存在复合幅相误差的阵元，导向矢量变为

$\begin{align}&{G}(\theta ) \!=\! {[{\alpha _{ - K}}\alpha _K^*{{\rm{e}}^{2{\rm{j}}{\mu _n}{m_{ - K}}}}\, ·\!·\!· \,{\alpha _{ - k}}\alpha _k^*{{\rm{e}}^{2{\rm{j}}{\mu _n}{m_{ - k}}}}\, ·\!·\!· \,{\alpha _0}\alpha _0^*]^\rm{T}}\\& = \begin{array}{*{20}{c}}{\left[\! {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{\alpha _{ - K}}\alpha _K^*}&0& ·\!·\!· &0\\0&\vdots &0& \vdots \\ \vdots &0&{{\alpha _{ - 1}}\alpha _1^*}&0\\0& ·\!·\!· &0&{{\alpha _0}\alpha _0^*}\end{array}}\end{array}} \!\right]}\end{array}\!\!\!\! \left[\! {\begin{array}{*{20}{c}}{{{\rm{e}}^{2{\rm{j}}{\mu _n}{m_{ - K}}}}}\\ \vdots \\{{{\rm{e}}^{2{\rm{j}}{\mu _n}{m_{ - 1}}}}}\\1\end{array}} \!\right]\\& = \left[ {\begin{array}{*{20}{c}}{\rm{diag}\left( {{{{1}}_{1 \times {{P}}}}} \right)}&{{{{0}}_{P \times M}}}\\{{{{0}}_{M \times P}}}&{{{{Γ}}_2}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{{{b}}_1}(\theta )}\\{{{{b}}_2}(\theta )}\end{array}} \right]\\&= \left( {\begin{array}{*{20}{c}}{{{b}_1}(\theta )}&{{{{0}}_{P \times (M + 1)}}}\\{{{{0}}_{(M + 1) \times 1}}}&{\rm{diag}\left[ {{{b}_2}(\theta )} \right]}\end{array}} \right)\left[ {\begin{array}{*{20}{c}}1\\{\rm{vecd}({{{Γ}}_2})}\end{array}} \right]\\& = {{T}_b}\left( \theta \right){d}\left( \theta \right)\end{align}$

(15)

式中， $P \times 1$ 维矢量 ${{b}_1}(\theta )$ 由 $2P$ 个精确校正的辅助阵元按对称阵元导向矢量的乘积组成， $(M + 1) \times 1$ 维矢量 ${{b}_2}(\theta )$ 是由存在幅相误差的 $2M + 1$ 个阵元按对称阵元导向矢量的乘积组成， ${{{Γ}}_2}$ 是 $(M + 1) \times$ $(M + 1)$ 维对角矩阵，由对称阵元相应的幅相误差的乘积组成， ${{T}_b}\left( \theta \right)$ 为只含方位角信息的 $\left( {K + 1} \right) \times$ $\left( {M + 2} \right)$ 维矩阵， ${{δ}}\left( \theta \right)$ 是 ${{{Γ}}_2}$ 中的误差项组成的 $\left( {M + 2} \right) \times 1$ 维列矢量。

从式(15)的变换过程可以看出：通过对阵元数为 $2K + 1$ ，阵元间距为 $\lambda /4$ 的等距均匀阵列的矢量重构，可以得到一个阵元数为 $K + 1$ ，阵元间距为 $\lambda /2$ 的虚拟等距均匀阵列，且这 $K + 1$ 个阵元中有 $P$ 个精确校正的阵元， $M + 1$ 个存在复合幅相误差的阵元。

那么，对重构的虚拟阵列的数据协方差矩阵 ${{R}_Y\;}$ 进行特征分解，得

${{R}_Y} \!=\! {\rm{E}}[{Y}\!(\!t)\!{{Y}^\rm{H}}\!(\!t)\!] \!=\! {{U}_{S1}}{{{Λ}} _{S1}}{U}_{S1}^{\rm{H}} \!+\! {{U}_{N1}}{{{Λ}} _{N1}}{U}_{N1}^\rm{H}$

(16)

其中， ${{{Λ}}_{S1}}$ 为大特征值组成的对角阵， ${{{Λ}}_{N1}}$ 为小特征值组成的对角阵， ${{U}_{S1}}$ 为大特征值对应的信号子空间， ${{U}_{N1}}$ 为小特征值对应的噪声子空间。

由子空间的正交性原理得

${{G}^\rm{H}}(\theta ){{U}_{N1}}{U}_{N1}^{\rm{H}}{G}(\theta ) = 0$

(17)

故将导向矢量即式(15)代入式(17)中，得

$\begin{align}& {{{δ}}^{\rm{H}}}\left( \theta \right){T}_b^{\rm{H}}\left( \theta \right){{U}_{N1}}{U}_{N1}^{\rm{H}}{{T}_b}\left( \theta \right){{δ}}\left( \theta \right)\\& = {{{δ}}^{\rm{H}}}\left( \theta \right){C}(\theta ){{δ}}\left( \theta \right) = 0\end{align}$

(18)

式中， ${C}(\theta )$ 为 $\left( {M + 2} \right) \times \left( {M + 2} \right)$ 维矩阵

${C}(\theta ) = {T}_b^{\rm{H}}\left( \theta \right){{U}_{N1}}{U}_{N1}^{\rm{H}}{{T}_b}\left( \theta \right)$

(19)

从式(17)、式(18)和式(19)中可以看出， ${{U}_{N1}}$ 为重构的虚拟阵列的数据协方差矩阵特征分解得到的噪声子空间， ${C}(\theta )$ 只含方位角的信息，并且通过式(15)可以得出 ${{δ}}\left( \theta \right)$ 为误差矢量，且 ${{δ}}\left( \theta \right) \ne 0$ 。所以，对信源的方位角进行估计，有

${\overset{\frown} \theta} = \arg \mathop {\max }\limits_\theta \frac{1}{{{\lambda _{\min }}\left[ {{C}(\theta )} \right]}}$

(20)

式中， ${\lambda _{\min }}\left[ \bullet \right]$ 表示求矩阵最小的特征值。

通过上面的分析得到：对虚拟阵列的变换，可成功将原来耦合的误差(复合的幅相误差)与方位角进行解耦合，即将导向矢量中的方位参数与虚拟阵元的误差分离，此时采用MUSIC算法1维搜索就可估计出信源的方位角。值得注意的是，此时的误差是两两阵元合成的，不能直接估计出原始阵元的误差参数，还需估计出信源的距离参数才能实现误差与距离的解耦合。

3.2 近场源的距离估计

通过上节得到了信号源方位角的估计值，将 ${\overset{\frown} \theta}$ 代入式(10)中，可以发现原始的阵列只存在了距离参数和误差的耦合，此时的阵列中存在 $2P$ 个精准校正的辅助阵元和 $2M + 1$ 个存在幅相误差扰动的阵元。故阵列的导向矢量为

$\begin{align}& \tilde{ a}({\overset{\frown} \theta} ,r) = {{Γ}}{a}({\overset{\frown} \theta} ,r)\\& = \left[ {\begin{array}{*{20}{c}}{{\alpha _{ - K}}}&0& \cdots &0\\0& \ddots & \ddots & \vdots \\ \vdots & \ddots &{{\alpha _{K - 1}}}&0\\0&0& \cdots &{{\alpha _K}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{{\rm{e^{j}}^\left( {{\mu _n}{n_{ - K}} + {\varphi _n}n_{ - K}^2} \right)}}}\\ \vdots \\{{{\rm{e^{j}}^\left( {{\mu _n}{n_{K - 1}} + {\varphi _n}n_{K - 1}^2} \right)}}}\\{{{\rm{e^{j}}^\left( {{\mu _n}{n_K} + {\varphi _n}n_K^2} \right)}}}\end{array}} \right]\\& = \left( {\begin{array}{*{20}{c}}{{{a}_1}({\overset{\frown} \theta} ,r)}&{{{0}_{P \times (2M + 1)}}}&{{{0}_{P \times 1}}}\\{{{0}_{(2M + 1) \times 1}}}&{{\rm{diag}}\left[ {{{a}_2}({\overset{\frown} \theta} ,r)} \right]}&{{{0}_{(2M + 1) \times 1}}}\\{{{0}_{P \times 1}}}&{{{0}_{P \times (2M + 1)}}}&{{{a}_3}({\overset{\frown} \theta} ,r)}\end{array}} \right)\\& \;\;\quad\cdot\left[ {\begin{array}{*{20}{c}}1\\{{\rm{vecd}}({{{Γ}}_1})}\\1\end{array}} \right]\\& = {{T}_a}\left( {{\overset{\frown} \theta} ,r} \right){{d}_1}\left( {{\overset{\frown} \theta} ,r} \right)\end{align}$

(21)

其中， ${{T}_a}\left( {{\overset{\frown} \theta} ,r} \right)$ 是 $\left( {2K + 1} \right) \times \left( {2M + 3} \right)$ 维矩阵， ${{{δ}}_1}\left( {{\overset{\frown} \theta} ,r} \right)$ 是 $\left( {2M + 3} \right) \times 1$ 维列矢量。由式(12)可知，存在误差时的MUSIC算法为

${\tilde {a}^\rm{H}}({\overset{\frown} \theta} ,r){\tilde {U}_N}\tilde {U}_N^{\rm{H}}\tilde {a}({\overset{\frown} \theta} ,r) = 0$

(22)

将式(21)代入到式(22)中，可以得到

$\begin{align}&{{{δ}}_1}^{\rm{H}}\left( {{\overset{\frown} \theta} ,r} \right){T}_a^{\rm{H}}\left( {{\overset{\frown} \theta} ,r} \right){\tilde{ U}_N}\tilde{ U}_N^{\rm{H}}{{T}_a}\left( {{\overset{\frown} \theta} ,r} \right){{{δ}}_1}\left( {{\overset{\frown} \theta} ,r} \right) \\&= {{{δ}}_1}^{\rm{H}}\left( {{\overset{\frown} \theta} ,r} \right){Q}({\overset{\frown} \theta} ,r){{{δ}}_1}\left( {{\overset{\frown} \theta} ,r} \right) = 0\end{align}$

(23)

式中， ${Q}({\overset{\frown} \theta} ,r)$ 为 $\left( {2M + 3} \right) \times \left( {2M + 3} \right)$ 维矩阵

${Q}({\overset{\frown} \theta} ,r) = {T}_a\!\!{^\rm{H}}\left( {{\overset{\frown} \theta} ,r} \right){\tilde {U}_N}\tilde {U}_N\!\!^{\rm{H}}{{T}_a}\left( {{\overset{\frown} \theta} ,r} \right)$

(24)

从式(22)、式(23)和式(24)中可以看出， ${Q}({\overset{\frown} \theta} ,r)$ 含估计的方位角的信息和待估计的距离参数，并且通过式(21)可以得出 ${{{δ}}_1}\left( {{\overset{\frown} \theta} ,r} \right)$ 是由当误差存在时原始阵列的幅相扰动误差 ${{{Γ}}_1}$ 构成的，且 ${{{δ}}_1}\left( {{\overset{\frown} \theta} ,r} \right) \ne {0}$ 。所以，对信源的距离进行估计，有

${\overset{\frown} r} = \arg \mathop {\max }\limits_r \frac{1}{{{\lambda _{\min }}\left[ {{Q}({\overset{\frown} \theta} ,r)} \right]}}$

(25)

很显然，上述的变换将原来耦合的误差与距离参数进行了解耦合，即将原始阵列的导向矢量中的距离与误差进行了分离，从而采用MUSIC算法1维搜索就将信源的距离估计出来。

3.3 近场源的误差校正及误差系数估计

通过前两节完成了方位与误差、距离与误差之间的解耦合，得到了近场源方位角及距离参数的估计值，将估计出的方位角和距离参数信息代入到式(24)得到 ${Q}({\overset{\frown} \theta} ,{\overset{\frown} r} )$ ，对其进行归一化运算，得到校正估计的误差系数，有

${{δ} _1}\left( {{\overset{\frown} \theta} ,{\overset{\frown} r} } \right) = {e_{\min }}\left[ {{Q}({\overset{\frown} \theta} ,{\overset{\frown} r} )} \right],{e_{\min }}\left( 1 \right)\; = 1$

(26)

${{α}} = {{{{{δ}}_1}}/{{{{δ}}_1}(1)}}$

(27)

其中， ${e_{\min }}\left[ \bullet \right]$ 是求矩阵最小特征值对应的特征矢量。由此，得出 ${{{Γ}}_1}$ 中均匀对称阵列通道幅相误差的估计值。

3.4 算法总结

基于上述分析，可将近场源利用辅助阵元矢量重构解耦合的幅相误差校正方法(Gain and phase calibration Instrumental sensor vector Reconstruction, GIR)的步骤总结如下：

步骤 1　按式(11)计算存在误差时的数据协方差矩阵 $\tilde {R}$ ，并按式(12)对其进行特征分解，获得存在误差时小特征值对应的噪声子空间 ${\tilde {U}_N}$ ；

步骤 2　按式(13)得到重新构造的虚拟阵列的数据 ${Y}$ ，按式(17)计算重构的虚拟阵列的数据协方差矩阵 ${{R}_Y\;}$ ，且对其进行特征分解得到噪声子空间 ${{U}_{N1}}$ ；

步骤 3　利用式(15)对虚拟的阵列导向矢量进行变换，按式(19)利用虚拟阵列的噪声子空间 ${{U}_{N1}}$ ，得到估计值 ${\overset{\frown} \theta}$ ；

步骤 4　在方位角估计值 ${\overset{\frown} \theta}$ 的基础上，将其代入式(10)得到含方位角估计信息、未知的距离参数信息以及误差系数的导向矢量 $\tilde {a}({\overset{\frown} \theta} ,r)$ ，利用式(21)对其进行变换，然后按式(24)利用步骤1中得到的噪声子空间 ${\tilde {U}_N}$ ，得到估计值 ${\overset{\frown} r}$ ；

步骤 5　在得到方位角估计值 ${\overset{\frown} \theta}$ 和距离估计值 ${\overset{\frown} r}$ 的基础上，按式(27)进行归一化运算得到阵元幅相误差系数的估计值。

4. 计算机仿真

通过仿真实验来验证GIR算法的有效性。对照图1，设均匀对称阵列总阵元数为13个，其中 $M = 4$ , $P = 2$ ，阵元位置矢量为 $[ - 6, - 5, - 4, - 3, - 2,$ $- 1,0,1,2,3,4,5,6]d$ ，且 $d = \lambda /4$ 。有一个独立的近场信号源入射到如图1所示的阵列上，信号源的参数为 $\theta = {0^ \circ }$ , $r = 3\lambda$ ，实验的快拍数为100，信噪比为20 dB，幅度误差2%、相位误差为 ${5^ \circ }$ ，噪声为零均值的高斯白噪声。

仿真1　阵元幅相误差的校正

GIR算法对幅相误差估计见表1。图2、图3给出了GIR算法对幅相误差校正后MUSIC算法的估计性能，以及误差已知情况下的MUSIC谱图和未进行误差校正时的MUSIC谱图。

表 1 各个通道误差系数的真实值、估计值以及差值

误差系数	阵元2	阵元3	阵元4	阵元5
真实值	1.0000+0.0000i	0.9822–0.0181i	0.9909–0.0688i	0.9889+0.0162i
估计值	1.0000+0.0000i	0.9820–0.0183i	0.9908–0.0686i	0.9885+0.0142i
差值的绝对值	0.0000+0.0000i	0.0003+0.0000i	0.0002+0.0000i	0.0020+0.0000i

误差系数	阵元6	阵元7	阵元8	阵元9
真实值	1.0167+0.0121i	0.9820+0.0447i	1.0068+0.0062i	1.0077+0.0573i
估计值	1.0153+0.0103i	0.9817+0.0442i	1.0050+0.0060i	1.0081+0.0564i
差值的绝对值	0.0022+0.0000i	0.0005+0.0000i	0.0019+0.0000i	0.0010+0.0000i

误差系数	阵元10	阵元11	阵元12
真实值	1.0103–0.0410i	0.9976–0.0580i	1.0000+0.0000i
估计值	1.0105–0.0402i	0.9973–0.0575i	0.9999–0.0007i
差值的绝对值	0.0008+0.0000i	0.0006+0.0000i	0.0007+0.0000i

下载: 导出CSV

| 显示表格

图 2 误差条件下方位角的MUSIC谱

下载: 全尺寸图片幻灯片

图 3 误差条件下距离的MUSIC谱

下载: 全尺寸图片幻灯片

由表1可得出GIR算法对幅相误差校正的精度较高。图2，图3表明未校正的MUSIC谱无法准确估计近场源方位角和距离，而GIR算法的谱图与已知误差的谱图基本重合，尤其在距离参数的估计方面，因此得出GIR算法对幅相误差校正以及对近场源定位比较准确。

仿真2　GIR算法校正精度与幅相误差的关系

比较GIR算法对幅相误差校正及近场源定位随幅度误差和相位误差变化的变化。图4，图5为幅度误差满足2%，相位误差分别为 ${0^ \circ }$ , ${5^ \circ }$ 和 ${30^ \circ }$ 时，GIR算法对误差校正性能随相位误差的变化。图6，图7为相位误差为 ${5^ \circ }$ ，幅度误差分别满足0, 2%, 50%时，GIR算法对误差校正性能随幅度误差的变化。图8，图9是幅度误差满足0, 2%, 50%，相应相位误差为 ${0^ \circ }$ , ${5^ \circ }$ 和 ${30^ \circ }$ 时，GIR算法对误差校正性能随相位误差和幅度误差的变化。

图4，图5表明幅度误差一定时，随相位误差增大，GIR算法的校正性能好，受相位误差影响较小。图6，图7表明相位误差一定时，随幅度误差的增大，GIR算法的校正效果有一定程度的下降，且在方位角估计方面下降效果明显。图8，图9表明随幅度误差和相位误差同时增大，GIR算法的校正效果受其影响小，3条曲线基本重合，校正估计结果精度高。

图 4 方位角的MUSIC谱随相位误差的变化

下载: 全尺寸图片幻灯片

图 5 距离的MUSIC谱随相位误差的变化

下载: 全尺寸图片幻灯片

图 6 方位角的MUSIC谱随幅度误差的变化

下载: 全尺寸图片幻灯片

图 7 距离的MUSIC谱随幅度误差的变化

下载: 全尺寸图片幻灯片

图 8 方位角的MUSIC谱随幅相误差的变化

下载: 全尺寸图片幻灯片

图 9 距离的MUSIC谱随幅相误差的变化

下载: 全尺寸图片幻灯片

仿真3　GIR算法统计性能分析

比较GIR算法与文献[12]，文献[15]的算法对幅相误差校正的统计特性随信噪比的变化。等距均匀阵列的阵元数为11，其中GIR算法、文献[12]辅助阵元数为4，有幅相误差的阵元数为7，进行100次蒙特卡洛实验。DOA和距离的RMSE随信噪比变化如图10，图11所示。

图 10 方位角的均方根误差随信噪比的变化

下载: 全尺寸图片幻灯片

图 11 距离的均方根误差随信噪比的变化

下载: 全尺寸图片幻灯片

从图10与图11中可以看出方位角和距离的RMSE随信噪比增大而减小，本文算法较文献[15]2维谱搜索方法计算量小、性能好，尤其在信噪比较高的情况下，GIR算法要远远好于比较算法，且GIR算法与误差已知时的统计性能相比，尤其在距离方面，曲线基本重合。图中文献[12]的算法在性能方面差，是因为文献[12]采用的辅助阵元法-ISM算法在近场条件下设置的辅助阵元达不到要求，且距离与方位是耦合的导致该算法不能直接在近场条件下使用。同时当信噪比达到20 dB时，GIR算法的均方根误差已接近为0，估计精度高。

5. 结束语

在近场源模型下，当阵列存在幅相误差时，误差与方位之间是耦合的，误差与距离之间是耦合的，方位与距离之间也是耦合的。所以多维参数的联合估计才可以求解，但计算复杂繁琐，且在阵元自由度不够的情况下，很难准确对近场源进行定位估计。针对近场源这一难题，本文提出一种近场源利用辅助阵元矢量重构解耦合的幅相误差校正方法。算法首先通过对阵元间距为 $\lambda /4$ 的等距均匀阵列重构得到一个阵元间距为 $\lambda /2$ 的虚拟等距均匀阵列，实现了距离参数的分离；再通过对虚拟阵列导向矢量的变换实现了方位与误差之间的解耦，从而估计出方位；然后利用估计出的方位参数对原始阵列导向矢量进行变换实现距离与误差之间的解耦，从而得到距离参数的估计值；最后利用得到的方位与距离的估计值以及原始阵列存在误差时的噪声子空间通过归一化运算得出阵元误差系数。相比传统不解耦的方法，该算法可以同时实现对近场源的方位角、距离以及阵元误差系数的级联估计，且只需进行2次1维谱搜索，避免了多维谱搜索，无需参数配对，计算量小，且在虚拟阵列重构过程中没有损失阵列孔径，所以角度和距离的估计精度高，幅相误差的校正精度高，可以实现实时估计，更符合实际应用的要求。最后通过计算机的仿真实验对该算法的有效性进行了验证。

图 1 具有CTDE框架和共享经验池的多智能体系统模型

下载: 全尺寸图片幻灯片

图 2 Dueling DQN网络结构示意图

下载: 全尺寸图片幻灯片

图 3 隶属度函数及质心解模糊法示意图

下载: 全尺寸图片幻灯片

图 4 干扰环境频谱瀑布图

下载: 全尺寸图片幻灯片

图 5 各算法性能比较图

下载: 全尺寸图片幻灯片

图 6 不同环境下算法性能比较

下载: 全尺寸图片幻灯片

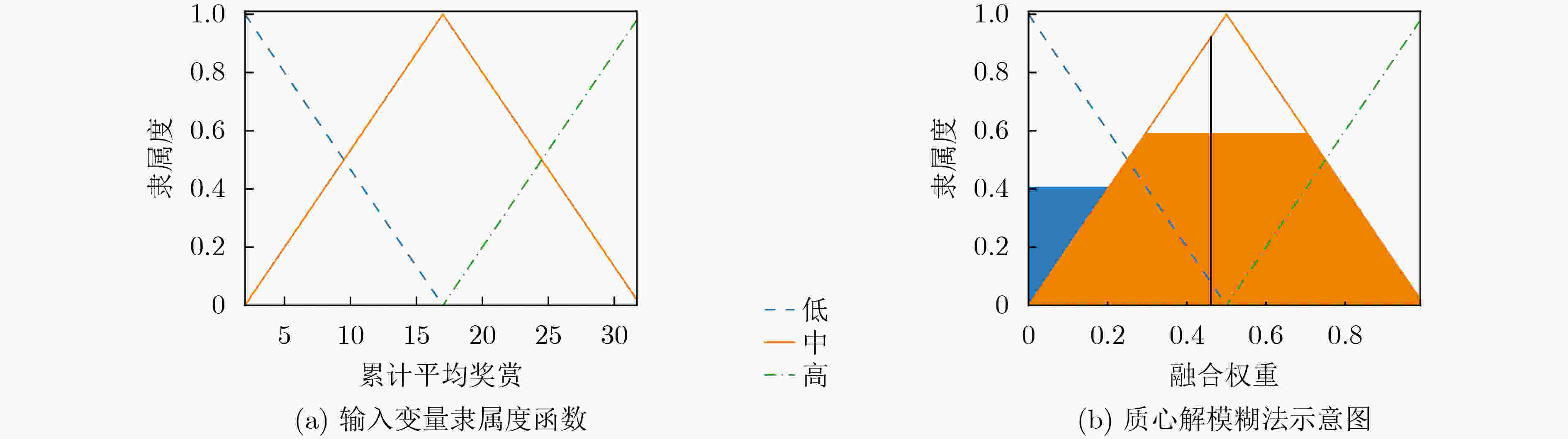
表 1 模糊规则定义

融合权重 ${w_{{F_i}}}$		累计平均奖赏 $r{'_i}$
融合权重 ${w_{{F_i}}}$		低	中	高
累计平均样本优先度 $g{'_i}$	低	中	高	高
	中	低	中	高
	高	低	低	中
区间	累计平均奖赏 $r{'_i}$	$\left[ {r{'_{\min }},r{'_{\max }}} \right]$
	累计平均样本优先度 $g{'_i}$	$\left[ {g{'_{\min }},g{'_{\max }}} \right]$
	融合权重 ${w_{{F_i}}}$	[0, 1]

下载: 导出CSV

参考文献(22)

[1]	WANG Qian, ZHANG Feng, ZHAO Jing, et al. Application of HBM2 data storage in time and frequency hopping network communication system[C]. The 2020 IEEE 6th International Conference on Computer and Communications, Chengdu, China, 2020: 1799–1803.
[2]	孙杜娟, 马迁, 王睿. 海上大型编队短波跳频组网问题研究[J]. 指挥控制与仿真, 2020, 42(1): 25–28. SUN Dujuan, MA Qian, and WANG Rui. Research on the large warship fleet HF frequency hopping network[J]. Command Control &Simulation, 2020, 42(1): 25–28.
[3]	王泽. 同步组网跳频电台网络系统的研究与实现[D]. [硕士论文], 北京化工大学, 2015. WANG Ze. Research and implementation of frequency-hopping radio network system with synchronous networking[D]. [Master dissertation], Beijing University of Chemical Technology, 2015.
[4]	古稀林, 王超, 冯志先, 等. 移动Ad-hoc网络中无线跳频频率资源分配机制研究[J]. 通信技术, 2019, 52(3): 646–652. GU Xilin, WANG Chao, FENG Zhixian, et al. Wireless hopping-frequency planning algorithm in mobile ad-hoc network[J]. Communications Technology, 2019, 52(3): 646–652.
[5]	崔佩璋, 全厚德, 张世杰. 跳频组网同频干扰消除方法研究[J]. 中国测试, 2014, 40(5): 115–118. doi: 10.11857/j.issn.1674-5124.2014.05.030 CUI Peizhang, QUAN Houde, and ZHANG Shijie. Research on eliminating co-channel interference of frequency-hopping communication network[J]. China Measurement &Test, 2014, 40(5): 115–118. doi: 10.11857/j.issn.1674-5124.2014.05.030
[6]	YOO S J, WON J M, SEO M, et al. Dynamic frequency hopping channel management in cognitive radio ad-hoc networks[C]. The 2015 21st Asia-Pacific Conference on Communications, Kyoto, Japan, 2015: 422–426.
[7]	罗明刚. 无线通信抗干扰技术分析[J]. 中国新通信, 2020, 22(12): 10–11. doi: 10.3969/j.issn.1673-4866.2020.12.009 LUO Minggang. Analysis of wireless communication anti-jamming technology[J]. China New Telecommunications, 2020, 22(12): 10–11. doi: 10.3969/j.issn.1673-4866.2020.12.009
[8]	陈前斌, 谭颀, 贺兰钦, 等. 云雾混合网络下基于多智能体架构的资源分配及卸载决策研究[J]. 电子与信息学报, 2021, 43(9): 2654–2662. doi: 10.11999/JEIT200256 CHEN Qianbin, TAN Qi, HE Lanqin, et al. Research on resource allocation and offloading decision based on multi-agent architecture in cloud-fog hybrid network[J]. Journal of Electronics &Information Technology, 2021, 43(9): 2654–2662. doi: 10.11999/JEIT200256
[9]	NAEEM F, SRIVASTAVA G, and TARIP M. A software defined network based fuzzy normalized neural adaptive multipath congestion control for the internet of things[J]. IEEE Transactions on Network Science and Engineering, 2020, 7(4): 2155–2164. doi: 10.1109/TNSE.2020.2991106
[10]	徐琳, 赵知劲. 基于CBR与合作Q学习的分布式CRN资源分配算法[J]. 电信科学, 2019, 35(2): 35–42. XU Lin and ZHAO Zhijin. A distributed CRN resource allocation algorithm based on CBR and cooperative Q-learning[J]. Telecommunications Science, 2019, 35(2): 35–42.
[11]	YANG Ning, ZHANG Haijun, and BERRY R. Partially observable multi-agent deep reinforcement learning for cognitive resource management[C]. 2020 IEEE Global Communications Conference, Taipei, China, 2020: 1–6. doi: 10.1109/GLOBECOM42002.2020.9322150.
[12]	MAJUMDAR A, BENAVIDEZ P, and JAMSHIDI M. Multi-agent exploration for faster and reliable deep Q-learning convergence in reinforcement learning[C]. 2018 World Automation Congress, Stevenson, USA, 2018: 1–6. doi: 10.23919/WAC.2018.8430409.
[13]	KONG Weiren, ZHOU Deyun, and YANG Zhen. Air combat strategies generation of CGF based on MADDPG and reward shaping[C]. 2020 International Conference on Computer Vision, Image and Deep Learning, Chongqing, China, 2020: 651–655. doi: 10.1109/CVIDL51233.2020.000-7.
[14]	李红光, 郭英, 张东伟, 等. 基于欠定盲源分离的同步跳频信号网台分选[J]. 电子与信息学报, 2021, 43(2): 319–328. doi: 10.11999/JEIT190920 LI Hongguang, GUO Ying, ZHANG Dongwei, et al. Synchronous frequency hopping signal network station sorting based on underdetermined blind source separation[J]. Journal of Electronics &Information Technology, 2021, 43(2): 319–328. doi: 10.11999/JEIT190920
[15]	MAN Jiaxi, LI Wei, WANG Hong, et al. On the technology of frequency hopping communication network-station selection[C]. 2021 International Conference on Electronics, Circuits and Information Engineering, Zhengzhou, China, 2021: 35–41. doi: 10.1109/ECIE52353.2021.00015.
[16]	JIANG Fu, ZHENG Chuyu, GAO Dianzhu, et al. A novel multi-agent cooperative reinforcement learning method for home energy management under a peak power-limiting[C]. 2020 IEEE International Conference on Systems, Man, and Cybernetics, Toronto, Canada, 2020: 350–355. doi: 10.1109/SMC42975.2020.9282976.
[17]	严季, 梁涛, 祈竹. 变跳速、变间隔跳频通信技术研究[J]. 无线通信技术, 2012, 21(4): 25–29. doi: 10.3969/j.issn.1003-8329.2012.04.006 YAN Ji, LIANG Tao, and QI Zhu. Research on the frequenct hopping communication technology of variable hopping rate and variable interval[J]. Wireless Communication Technology, 2012, 21(4): 25–29. doi: 10.3969/j.issn.1003-8329.2012.04.006
[18]	LI Menglin, CHEN Shaofei, and CHEN Jing. Adaptive learning: A new decentralized reinforcement learning approach for cooperative multiagent systems[J]. IEEE Access, 2020, 8: 99404–99421. doi: 10.1109/ACCESS.2020.2997899
[19]	叶梓峰, 王永华, 万频, 等. 基于优先记忆库结合竞争深度Q网络的动态功率控制[J]. 电讯技术, 2019, 59(10): 1132–1139. doi: 10.3969/j.issn.1001-893x.2019.10.004 YE Zifeng, WANG Yonghua, WAN Pin, et al. A dynamic power control strategy based on dueling deep Q network with prioritized experience replay[J]. Telecommunication Engineering, 2019, 59(10): 1132–1139. doi: 10.3969/j.issn.1001-893x.2019.10.004
[20]	HUANG Chong, ZHONG Jie, GONG Yu, et al. Novel deep reinforcement learning-based delay-constrained buffer-aided relay selection in cognitive cooperative networks[J]. Electronics Letters, 2020, 56(21): 1148–1150. doi: 10.1049/el.2020.1495
[21]	王雪, 金涛, 钱志鸿, 等. D2D中继辅助通信的能效优化算法研究[J]. 通信学报, 2020, 41(3): 71–79. doi: 10.11959/j.issn.1000-436x.2020048 WANG Xue, JIN Tao, QIAN Zhihong, et al. Research on maximizing energy efficiency for relay-aided D2D communication[J]. Journal on Communications, 2020, 41(3): 71–79. doi: 10.11959/j.issn.1000-436x.2020048
[22]	LIU Xin, XU Yuhua, JIA Luliang, et al. Anti-jamming communications using spectrum waterfall: A deep reinforcement learning approach[J]. IEEE Communications Letters, 2018, 22(5): 998–1001. doi: 10.1109/LCOMM.2018.2815018

施引文献

期刊类型引用(4)

1.	杨昆，付浩，王雪迪，吴琼，吴瑾. 气象卫星遥感数据接收异常诊断系统设计. 计算机测量与控制. 2024(11): 9-17 . 百度学术
2.	万鹏程，冯为可，童宁宁，韦伟. 一种面向时变射频干扰的时频特征预测网络. 西北工业大学学报. 2023(03): 587-594 . 百度学术
3.	吕增光. 广播电视自动监控系统主要技术分析. 电视技术. 2021(06): 144-146 . 百度学术
4.	尉景辉，柳贤子. 卫星接收机干扰抑制关键技术的研究与实现. 数字传媒研究. 2021(12): 7-9+16 . 百度学术

其他类型引用(1)

资源附件(0)

访问统计

图(6) / 表(1)

计量

文章访问数: 1729
HTML全文浏览量: 873
PDF下载量: 209
被引次数: 5

1. 引言
2. 近场源阵列幅相误差的信号模型
2.1 阵列模型
2.2 误差条件下的数据模型
3. 近场源幅相误差校正算法
3.1 近场源的DOA估计
3.2 近场源的距离估计
3.3 近场源的误差校正及误差系数估计
3.4 算法总结
4. 计算机仿真
5. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于多智能体模糊深度强化学习的跳频组网智能抗干扰决策算法

doi: 10.11999/JEIT210608

通讯作者:
朱家晟　1045314503@qq.com

计量

Intelligent Anti-jamming Decision Algorithm for Frequency Hopping Network Based on Multi-agent Fuzzy Deep Reinforcemnet Learning

1. 引言

2. 近场源阵列幅相误差的信号模型

2.1 阵列模型

2.2 误差条件下的数据模型

3. 近场源幅相误差校正算法

3.1 近场源的DOA估计

3.2 近场源的距离估计

3.3 近场源的误差校正及误差系数估计

3.4 算法总结

4. 计算机仿真

5. 结束语

期刊类型引用(4)

其他类型引用(1)

计量

目录

1. 引言

2. 近场源阵列幅相误差的信号模型

2.1 阵列模型

2.2 误差条件下的数据模型

3. 近场源幅相误差校正算法

3.1 近场源的DOA估计

3.2 近场源的距离估计

3.3 近场源的误差校正及误差系数估计

3.4 算法总结

4. 计算机仿真

5. 结束语

留言板

基于多智能体模糊深度强化学习的跳频组网智能抗干扰决策算法

doi: 10.11999/JEIT210608

通讯作者: 朱家晟 1045314503@qq.com

计量

出版历程

Intelligent Anti-jamming Decision Algorithm for Frequency Hopping Network Based on Multi-agent Fuzzy Deep Reinforcemnet Learning

1. 引言

2. 近场源阵列幅相误差的信号模型

2.1 阵列模型

2.2 误差条件下的数据模型

3. 近场源幅相误差校正算法

3.1 近场源的DOA估计

3.2 近场源的距离估计

3.3 近场源的误差校正及误差系数估计

3.4 算法总结

4. 计算机仿真

5. 结束语

期刊类型引用(4)

其他类型引用(1)

计量

出版历程

目录

1. 引言

2. 近场源阵列幅相误差的信号模型

2.1 阵列模型

2.2 误差条件下的数据模型

3. 近场源幅相误差校正算法

3.1 近场源的DOA估计

3.2 近场源的距离估计

3.3 近场源的误差校正及误差系数估计

3.4 算法总结

4. 计算机仿真

5. 结束语

通讯作者:
朱家晟　1045314503@qq.com