Extracting UWB One-Dimensional Scattering Center Based on Improved Matrix Pencil
-
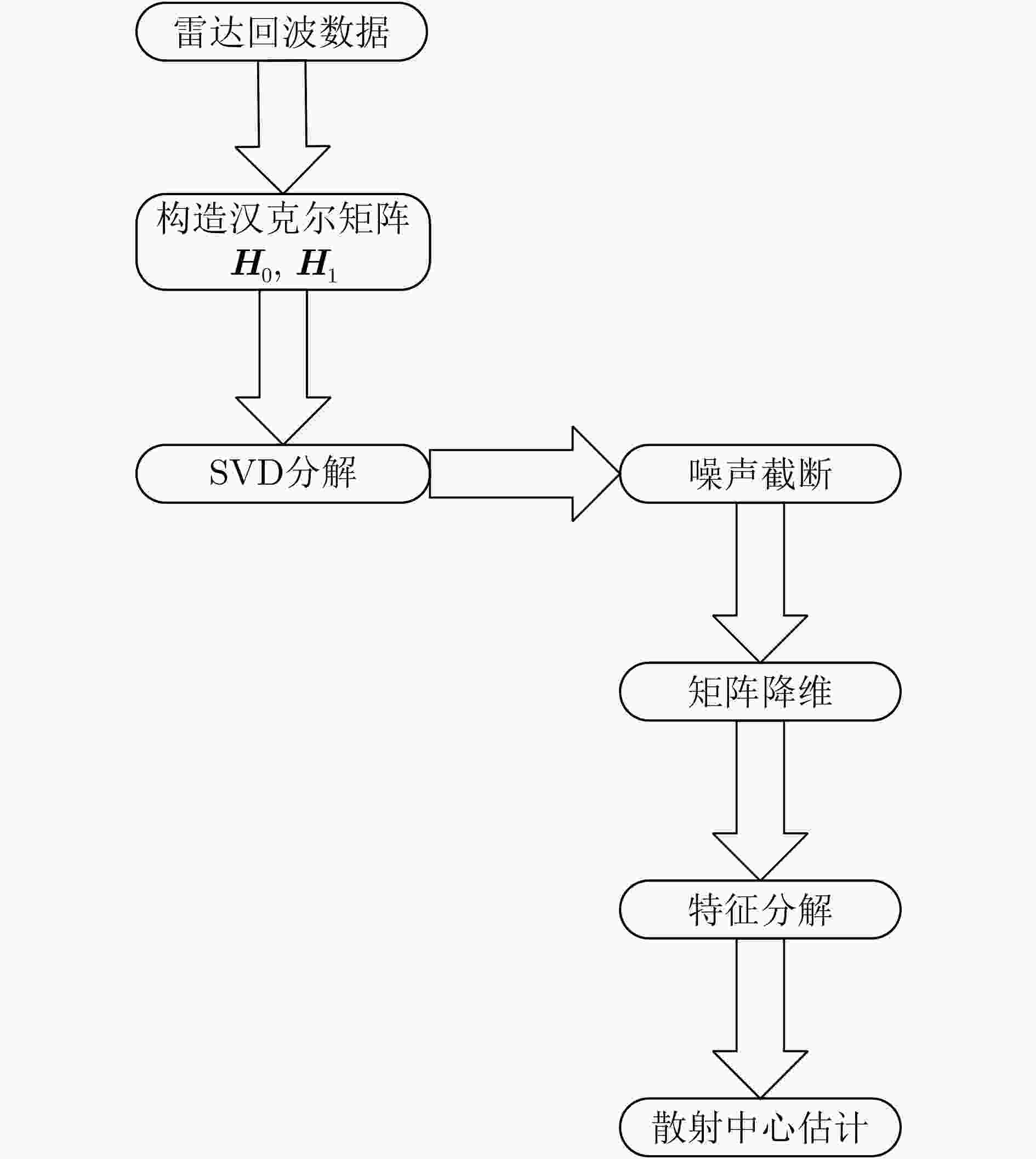
摘要: 针对微动参数的高精度快速估计问题,该文提出一种基于几何绕射(GTD)模型和改进矩阵束的超宽带(UWB)散射中心提取算法,可实现散射中心径向距离、类型参数及散射强度的同时估计。该方法将超宽带条件下的目标GTD散射模型转化为状态空间方程,利用奇异值分解将汉克尔矩阵中的噪声分量去除,对降秩的汉克尔矩阵做广义特征值分解,利用单个脉冲内最强的若干散射点构造回波估计,进而获得径向距离的估计;在准确估计距离参数的条件下,对模型参数解耦,使得类型参数与其他参数分离,通过最小二乘算法和搜索算法获得类型参数的估计;最后基于最小二乘法估计出散射中心的散射强度。仿真结果表明,改进的矩阵束方法在低信噪比(SNR)下具有好的鲁棒性,可快速且高精度地提取目标微动距离、类型参数和散射强度等信息。Abstract: In order to estimate the micro-motion parameters accurately and fleetly, an Ultra Wide Band (UWB) scattering center extraction algorithm based on Geometrical Theory of Diffraction (GTD) model and improved matrix pencil is proposed. The radial distance of the scattering center, the type parameters and the scattering intensity can be estimated simultaneously. The target GTD scattering model under UWB condition is transformed into a state space equation in this method, and the singular value decomposition is used to remove the noise component from the Hankel matrix. The generalized eigenvalue decomposition of the reduced Hankel matrix is performed, and the echo estimation is constructed by using the strongest scattering points in a single pulse, and then the radial distance estimation is obtained. Under the condition that the distance parameters are accurately estimated, the model parameters are decoupled so that the type parameters are separated from other parameters, and the type parameters are estimated by the least square algorithm and the search algorithm. Finally, the scattering intensity of the scattering center is estimated based on the least square method. The simulation results show that the improved matrix beam method has good robustness under low SNR, and can extract the target micro-motion distance, type parameters and scattering intensity with high precision.
-
表 1 类型参数代表的几何特征
参数值 散射中心的几何特征 –4/2 边缘上曲率不连续点 –2/2 锥尖 –1/2 弯曲边缘衍射 0/2 双曲面,平直的边缘 +1/2 单曲面(柱面) +2/2 角反射器,平面 表 2 散射中心参数估计的仿真参数设置
参数名称 数值 频率间隔$\Delta f$ 10 MHz 频率点数 201 中心频率${f_{\text{c}}}$ 10 GHz 信号采样间隔$\Delta t$ 0.001 s 时间窗口 19 总体仿真时间 1 s 表 3 加噪声情况下各算法的类型参数估计准确率及算法运行时间
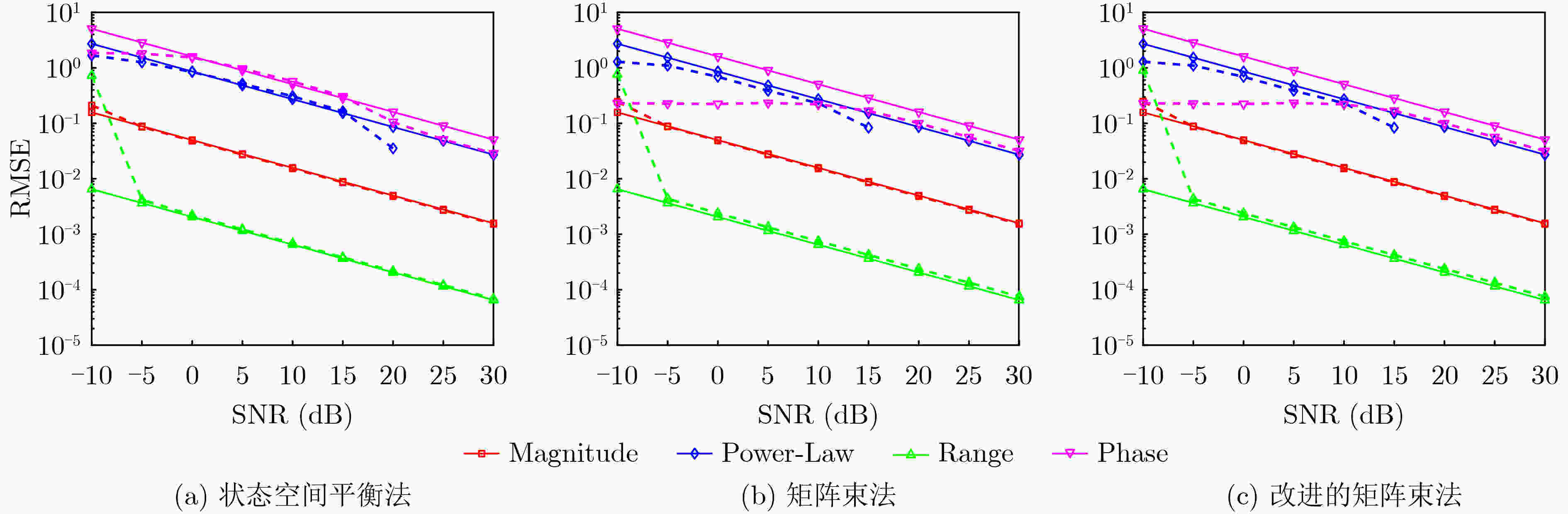
算法名称 类型参数估计准确率(%) 算法运行时间(s) 状态空间平衡法 28.60 32.1984 矩阵束法 46.20 34.3592 改进的矩阵束法 46.14 17.1721 -
[1] KELLER J B. Geometrical theory of diffraction[J]. Journal of the Optical Society of America, 1962, 52(2): 116–130. doi: 10.1364/JOSA.52.000116 [2] WANG Jing, WANG Fei, and ZHOU Jianjiang. Radar target scattering center extraction based on the full-polarization GTD model[C]. 2009 International Joint Conference on Computational Sciences and Optimization, Sanya, China, 2009: 882–885. [3] HURST M and MITTRA R. Scattering center analysis via Prony’s method[J]. IEEE Transactions on Antennas and Propagation, 1987, 35(8): 986–988. doi: 10.1109/TAP.1987.1144210 [4] STEEDLY W M and MOSES R L. High resolution exponential modeling of fully polarized radar returns[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(3): 459–469. doi: 10.1109/7.81427 [5] CARRIERE R and MOSES R L. High resolution radar target modeling using a modified Prony estimator[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(1): 13–18. doi: 10.1109/8.123348 [6] 徐嘉华, 张小宽, 郑舒予, 等. 基于改进3D-ESPRIT算法的GTD模型参数估计与目标识别[J]. 系统工程与电子技术, 2021, 43(2): 336–342. doi: 10.12305/j.issn.1001-506X.2021.02.07XU Jiahua, ZHANG Xiaokuan, ZHENG Shuyu, et al. GTD model parameter estimation and target recognition based on improved 3D-ESPRIT algorithm[J]. Systems Engineering and Electronics, 2021, 43(2): 336–342. doi: 10.12305/j.issn.1001-506X.2021.02.07 [7] DING Baiyuan and WEN Gongjian. A region matching approach based on 3-D scattering center model with application to SAR target recognition[J]. IEEE Sensors Journal, 2018, 18(11): 4623–4632. doi: 10.1109/JSEN.2018.2828307 [8] LI Tingli and DU Lan. SAR automatic target recognition based on attribute scattering center model and discriminative dictionary learning[J]. IEEE Sensors Journal, 2019, 19(12): 4598–4611. doi: 10.1109/JSEN.2019.2901050 [9] ZHOU Jianxiong, SHI Zhiguang, CHENG Xiao, et al. Automatic target recognition of SAR images based on global scattering center model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3713–3729. doi: 10.1109/TGRS.2011.2162526 [10] 郑舒予, 张小宽, 郭艺夺, 等. 一维GTD散射中心模型参数估计的改进MUSIC算法[J]. 北京航空航天大学学报, 2020, 46(11): 2149–2155. doi: 10.13700/j.bh.1001-5965.2019.0576ZHENG Shuyu, ZHANG Xiaokuan, GUO Yiduo, et al. Parameter estimation of 1D GTD scattering center model based on an improved MUSIC algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(11): 2149–2155. doi: 10.13700/j.bh.1001-5965.2019.0576 [11] ZHENG Shuyu, ZHANG Xiaokuan, ZONG Binfeng, et al. GTD model parameters estimation based on improved LS-ESPRIT algorithm[C]. 2019 Photonics & Electromagnetics Research Symposium, Xiamen, China, 2019: 2282–2289. [12] MITCHELL J and TJUATJA S. Separation of scattering phenomena in super-resolution ISAR imaging using constrained music[C]. 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 2015: 1586–1589. [13] KUNG S Y, ARUN K S, and RAO D V B. State-space and singular-value decomposition-based approximation methods for the harmonic retrieval problem[J]. Journal of the Optical Society of America, 1983, 73(12): 1799–1811. doi: 10.1364/JOSA.73.001799 [14] NAISHADHAM K and PIOU J E. A robust state space model for the characterization of extended returns in radar target signatures[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(6): 1742–1751. doi: 10.1109/TAP.2008.916932 [15] PIOU J E. A state identification method for 1-D measurements with gaps[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, USA, 2005: 1–9. [16] NAISHADHAM K and PIOU J E. State-space spectral estimation of characteristic electromagnetic responses in wideband data[J]. IEEE Antennas and Wireless Propagation Letters, 2005, 4: 406–409. doi: 10.1109/LAWP.2005.859386 [17] PIOU J E, CUOMO K M, and MAYHAN J T. A state-space technique for ultrawide-bandwidth coherent processing[R]. ESC-TR-98-066, 1999. [18] 闫华, 张磊, 陆金文, 等. 任意多次散射机理的GTD散射中心模型频率依赖因子表达[J]. 雷达学报, 2021, 10(3): 370–381. doi: 10.12000/JR21005YAN Hua, ZHANG Lei, LU Jinwen, et al. Frequency-dependent Factor Expression of the GTD scattering center model for the arbitrary multiple scattering mechanism[J]. Journal of Radars, 2021, 10(3): 370–381. doi: 10.12000/JR21005 [19] WANG Jun, WEN Yaya, WEI Shaoming, et al. A state-space approach for shape reconstruction of scattering targets with step-frequency radar[C]. The 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 2012: 1759–1763. [20] CHEN Xuan, TIAN Yuguang, DONG Chunzhu, et al. An improved state space approach based method for extracting the target scattering center[C]. 2017 International Applied Computational Electromagnetics Society Symposium, Suzhou, China, 2017: 1–3. [21] WEI Zhu, XIN He, JUN Hu, et al. Scattering centers extraction based on compressed sensing and multilevel fast multipole algorithm acceleration[C]. 2018 IEEE International Conference on Computational Electromagnetics, Chengdu, China, 2018: 1–2. [22] REN Lingyun, TRAN N, FOROUGHIAN F, et al. Short-time state-space method for micro-Doppler identification of walking subject using UWB impulse Doppler radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(7): 3521–3534. doi: 10.1109/TMTT.2018.2829523 [23] 姜卫东. 光学区雷达目标结构成像的理论及其在雷达目标识别中的应用[D]. [博士论文], 中国人民解放军国防科学技术大学, 2000.JIANG Weidong. Theory of radar target structure imaging in optical region and its application in radar target recognition[D]. [Ph. D. dissertation], National University of Defense Technology, 2000. [24] 牛晓红. 基于矩阵束和Prony的多正弦信号参数估计算法研究[D]. [硕士论文], 哈尔滨工程大学, 2017.NIU Xiaohong. Research on parameter estimation algorithm of multi-sinusoidal signal based on matrix bundle and Prony[D]. [Master dissertation], Harbin Engineering University, 2017. [25] HUA Y and SARKAR T K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(5): 814–824. doi: 10.1109/29.56027 [26] CUOMO K M, PION J E, and MAYHAN J T. Ultrawide-band coherent processing[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(6): 1094–1107. doi: 10.1109/8.777137 [27] HUA Y and SARKAR T K. Matrix pencil method and its performance[C]. International Conference on Acoustics, Speech, and Signal Processing, New York, USA, 1988: 2476–2479. [28] AKAIKE H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716–723. doi: 10.1109/TAC.1974.1100705 [29] WAX M and KAILATH T. Detection of signals by information theoretic criteria[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(2): 387–392. doi: 10.1109/TASSP.1985.1164557 [30] RISSANEN J. Modeling by shortest data description[J]. Automatica, 1978, 14(5): 465–471. doi: 10.1016/0005-1098(78)90005-5 [31] WAX M and ZISKIND I. Detection of the number of coherent signals by the MDL principle[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(8): 1190–1196. doi: 10.1109/29.31267 [32] HOLL JR D J. State-space approaches to ultra-wideband Doppler processing[D]. [Ph. D. dissertation], Worcester Polytechnic Institute, 2007. -





 下载:
下载:


 下载:
下载:
