Logging Curve Recovery Based on LSTM Multi-scale Symbiotic Relationship Mining
-
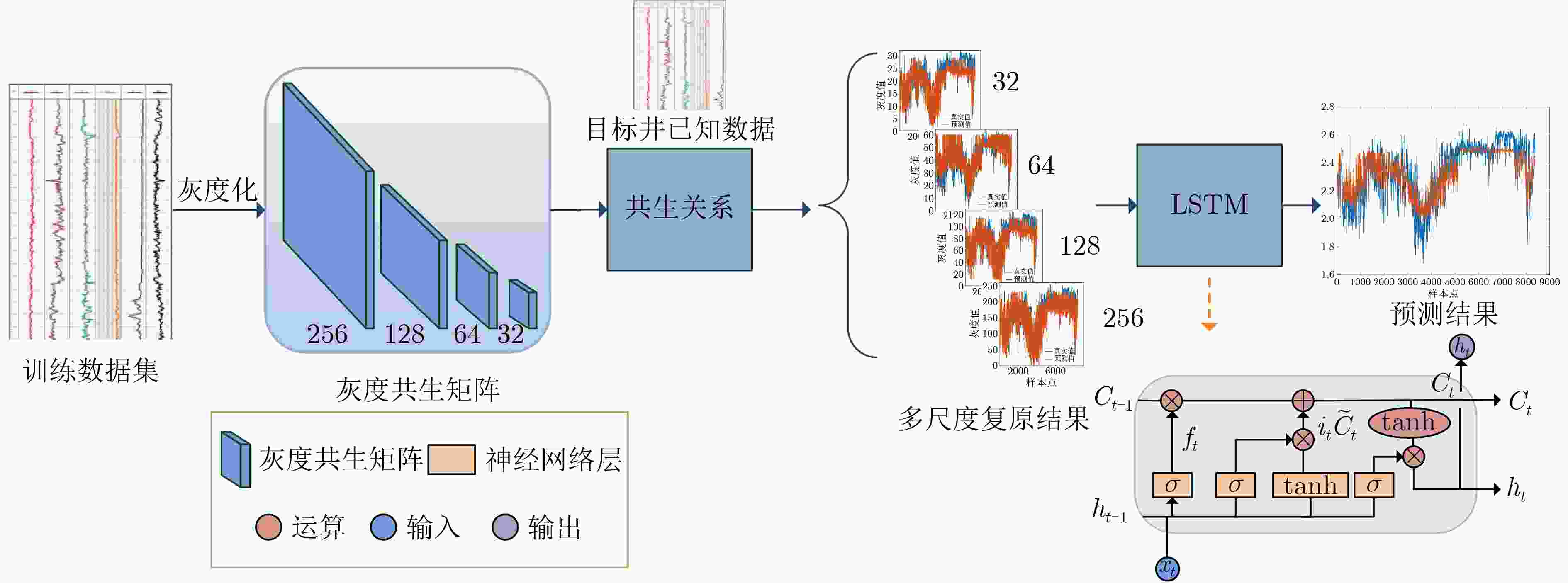
摘要: 利用测井数据进行储层地质描述的应用中,经常出现部分测井曲线失真或缺失的问题,为此,测井曲线复原一直以来都是相关研究领域的研究热点和难点。传统信号复原方法和基于神经网络等机器学习的复原方法,对同井不同测井曲线间关联信息的表示和利用不充分,跨井模型适应能力差。针对这些问题,该文提出一种基于长短时记忆(LSTM)网络多尺度共生关系挖掘的测井曲线复原方法:在基于神经网络测井曲线复原方法的基础上,通过引入多尺度灰度共生短阵(GLCM)关系完成对不同测井曲线间横向关联信息的表征以实现测井曲线集纵横向语义信息的全面利用,进而实现缺失测井曲线的复原。实验结果表明,与BP神经网络、随机森林(RF)、GBDT、深度森林(DF)和LSTM网络方法相比,该文所提方法具有更好的信号复原精度,且所构建模型具有一定的井间适应能力。Abstract: In the application of reservoir geological description using logging data, some of the logging curves are often distorted or missing, and for this reason, the recovery of logging curves is a research hotspot and difficulty in related research fields. Traditional signal recovery methods and recovery methods based on machine learning such as neural networks do not adequately represent and utilize correlation information between different logging curves of the same well, and have poor adaptability to cross-well models. In response to these problems, a log curve restoration method is proposed in this paper based on Long Short-Term Memory (LSTM) neural network multi-scale symbiosis mining: on the basis of neural network log curve restoration method, by introducing the multi-scale Gray Level Co-occurrence Matrix (GLCM) completes the characterization of the lateral correlation information between different logging curves so as to realize the full utilization of the vertical and horizontal semantic information of the logging curve set, thereby realizing the restoration of missing logging curves. The experimental results show that, compared with the BP neural network, Random Forest (RF), Gradient Boosting Decision Tree (GBDT), Deep Forest (DF) and LSTM network methods, the method proposed in this paper has better signal restoration accuracy, and the constructed model has a certain cross-well adaptability.
-
表 1 基于LSTM多尺度共生关系挖掘的测井曲线复原算法
输入:训练数据集${\boldsymbol{P} } = \left\{ { { {\boldsymbol{p} }_i} \in {R^{M \times 1} },i = 1,2, \cdots ,N} \right\}$,目标井
数据集
${\boldsymbol{P} }_r^{ {{\rm{target}}} } = \left\{ { {\boldsymbol{p} }_i^{ {\text{target} } } \in {R^{ {M_t} \times 1} },i = 1,2, \cdots ,N - 1} \right\}$输出:复原目标曲线$ {\boldsymbol{p}}_N^{{\text{target}}} \in {R^{{M_t} \times 1}} $ 相关模型训练: (1) 将训练数据集进行多尺度灰度化; (2) 生成灰度共生矩阵集${\bf{GLCM} } = {\left\{ { { {\bf{GLCM} }_i} } \right\}_{i = 1,2, \cdots ,N - 1} }$; (3) 训练生成式(5)中的$ {\beta _1} $和$ {\beta _2} $; (4) 训练多尺度灰度共生关系测井曲线复原LSTM网络; 测试井未知曲线复原: (5) 测试井已知母曲线多尺度灰度化; (6) 令$ {g_j} \in [32,64,128,256] $为4个多尺度灰度级,进行多尺度
曲线复原:For j=1:4 (a) 直接共生关系复原目标曲线$ {\boldsymbol{p}}_{N,{\text{dir}}}^{{\text{target}}} $; (b) 鲁棒共生关系复原目标曲线$ {\boldsymbol{p}}_{N,{\text{rob}}}^{{\text{target}}} $: For m=1:Mt ① If m==1,复制步骤(6a)得到目标曲线样本
序号为1的值;② If m==m+1,更新灰度共生矩阵后获取直
接共生关系复原值;③ m=m+1,依次进行迭代; End (c) 利用式(5)完成目标曲线融合:
$ {\boldsymbol{p}}_{N,{\text{glcm}}}^{{\text{target}}} = {\beta _1}{\boldsymbol{p}}_{N,{\text{dir}}}^{{\text{target}}} + {\beta _2}{\boldsymbol{p}}_{N,{\text{rob}}}^{{\text{target}}} $End (7) 得到的多尺度复原结果结合LSTM网络最终复原出目标曲线。 表 2 各个方法超参数设置表
方法 参数设置 BP神经网络 隐藏层为9,学习率为0.01,最大迭代次数为200,训练精度阈值为10–3 随机森林 树的个数为50,最大叶子数为10 GBDT 学习率为0.1,最大深度为3,最小叶子树为1 深度森林 最大层数为20,树的个数为100,最小叶子树为1,每个级联层的森林个数为2 LSTM网络 隐藏层单元个数为100,学习率为0.005,迭代次数为15,梯度下降算法设置为Adam 表 3 A1、A2井多尺度下DEN测井曲线复原定量结果
PCC RMSE MAPE(%) MAE A1井:32级 0.7817 0.0449 21.33 3.3376 A1井:64级 0.7702 0.0870 15.16 6.1063 A1井:128级 0.7802 0.1836 26.67 13.4370 A1井:256级 0.7702 0.3840 28.64 28.1911 A2井:32级 0.7592 0.0513 20.65 3.4353 A2井:64级 0.7297 0.1035 23.35 7.0856 A2井:128级 0.7285 0.2119 26.06 14.6945 A2井:256级 0.7258 0.4490 34.12 30.6630 表 4 A1井6组近邻点DEN复原定量结果
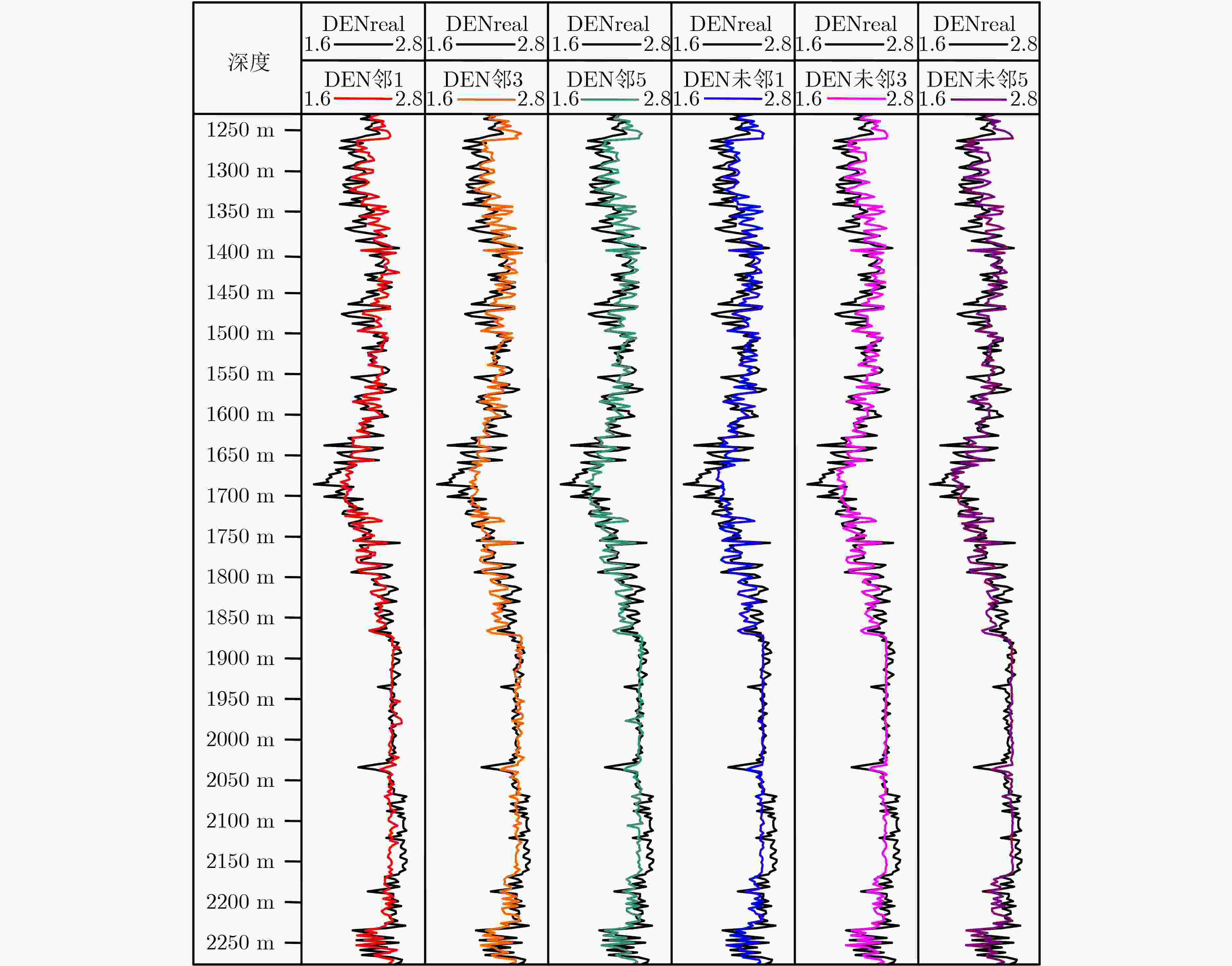
PCC RMSE MAPE(%) MAE 邻1 0.8382 0.0011 3.47 0.0806 邻3 0.8348 0.0011 3.54 0.0819 邻5 0.8475 0.0011 3.45 0.0785 未邻1 0.8282 0.0012 3.59 0.0830 未邻3 0.8385 0.0011 3.51 0.0812 未邻5 0.8400 0.0011 3.46 0.0797 表 5 不同模型复原A1、A2井DEN的定量结果
PCC RMSE MAPE(%) MAE A1井 A2井 A1井 A2井 A1井 A2井 A1井 A2井 BP神经网络 0.7817 0.5948 0.0014 0.0015 4.45 4.80 0.1028 0.1157 随机森林 0.8175 0.7551 0.0014 0.0017 4.38 5.39 0.0987 0.1319 GBDT 0.8239 0.6942 0.0012 0.0025 4.05 9.13 0.0936 0.2008 深度森林 0.8352 0.7805 0.0013 0.0016 4.15 5.24 0.0966 0.1194 LSTM网络 0.8201 0.7809 0.0012 0.0012 3.87 3.56 0.0879 0.0831 本文方法 0.8475 0.7860 0.0011 0.0011 3.45 3.23 0.0785 0.0758 表 6 不同模型DEN谱分析定量结果
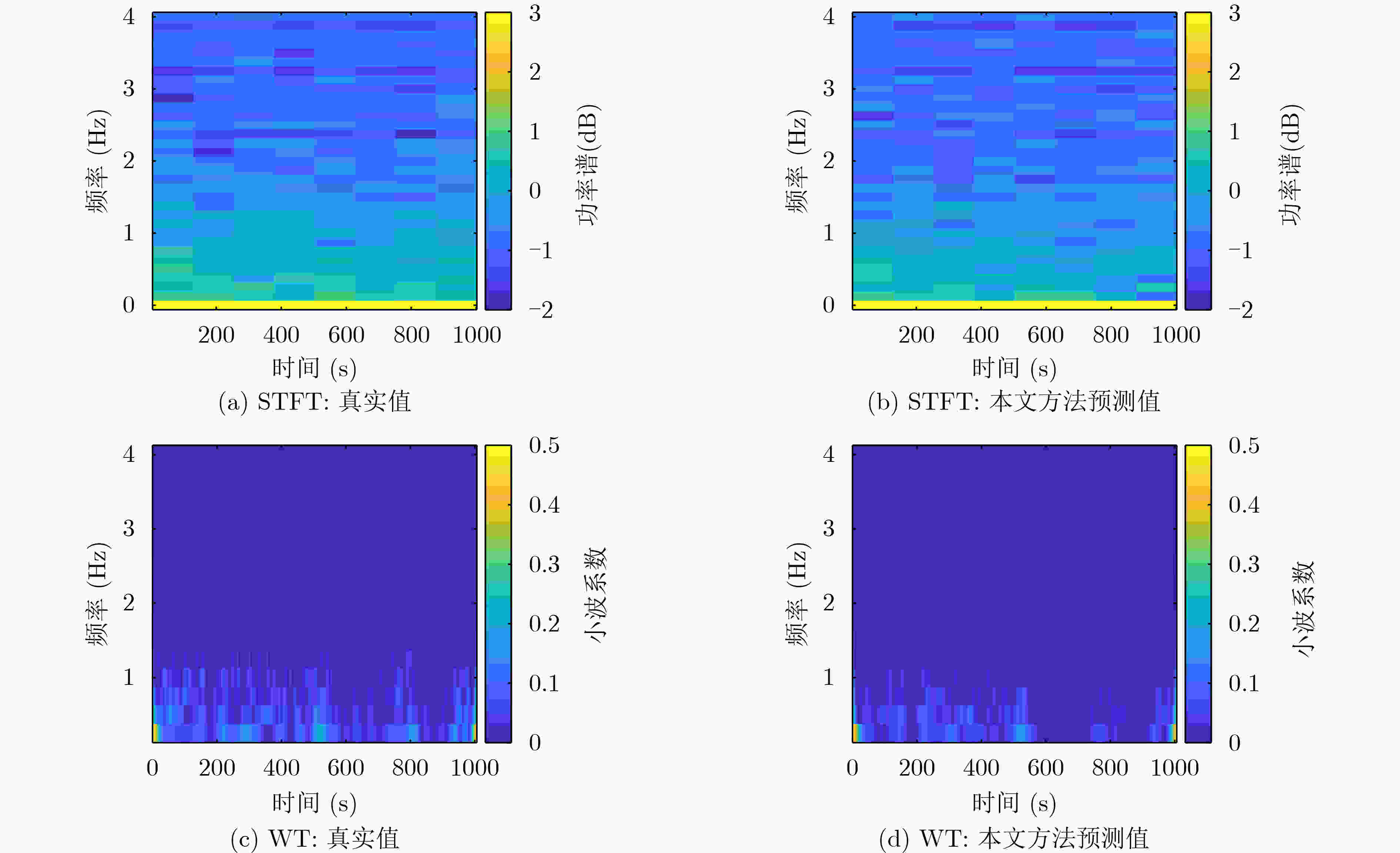
STFT WT PCC (A1, A2) MAE (A1, A2) PCC (A1, A2) MAE (A1, A2) BP神经网络 0.9098 0.9034 0.2609 0.2688 0.8649 0.8319 0.0090 0.0095 随机森林 0.9007 0.8778 0.2829 0.3482 0.8073 0.8632 0.0109 0.0102 GBDT 0.8999 0.8639 0.2934 0.3542 0.8306 0.8505 0.0109 0.0106 深度森林 0.9141 0.8421 0.2612 0.4461 0.8114 0.8505 0.0106 0.0124 LSTM网络 0.9218 0.9241 0.2570 0.2592 0.8703 0.8201 0.0099 0.0103 本文方法 0.9193 0.9249 0.2580 0.2382 0.8743 0.8784 0.0093 0.0079 -
[1] 张东晓, 陈云天, 孟晋. 基于循环神经网络的测井曲线生成方法[J]. 石油勘探与开发, 2018, 45(4): 598–607. doi: 10.11698/PED.2018.04.06ZHANG Dongxiao, CHEN Yuntian, and MENG Jin. Synthetic well logs generation via recurrent neural networks[J]. Petroleum Exploration and Development, 2018, 45(4): 598–607. doi: 10.11698/PED.2018.04.06 [2] 王俊瑞, 梁力文, 邓强, 等. 基于多元回归模型重构测井曲线的方法研究及应用[J]. 岩性油气藏, 2016, 28(3): 113–120. doi: 10.3969/j.issn.1673-8926.2016.03.015WANG Junrui, LIANG Liwen, DENG Qiang, et al. Research and application of log reconstruction based on multiple regression model[J]. Lithologic Reservoirs, 2016, 28(3): 113–120. doi: 10.3969/j.issn.1673-8926.2016.03.015 [3] WANG Guochang, CARR T R, JU Yiwen, et al. Identifying organic-rich Marcellus Shale lithofacies by support vector machine classifier in the Appalachian basin[J]. Computers & Geosciences, 2014, 64: 52–60. doi: 10.1016/j.cageo.2013.12.002 [4] SALEHI M M, RAHMATI M, KARIMNEZHAD M, et al. Estimation of the Non records logs from existing logs using artificial neural networks[J]. Egyptian Journal of Petroleum, 2017, 26(4): 957–968. doi: 10.1016/j.ejpe.2016.11.002 [5] ROLON L, MOHAGHEGH S D, AMERI S, et al. Using artificial neural networks to generate synthetic well logs[J]. Journal of Natural Gas Science and Engineering, 2009, 1(4/5): 118–133. doi: 10.1016/j.jngse.2009.08.003 [6] 陈云天. 基于机器学习的测井曲线补全与生成研究[D]. [博士论文], 北京大学, 2020.CHEN Yuntian. Research on well log completion and generation based on machine learning[D]. [Ph. D. dissertation], Peking University, 2020. [7] BAI Jing, DING Bixiu, XIAO Zhu, et al. Hyperspectral image classification based on deep attention graph convolutional network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5504316. doi: 10.1109/TGRS.2021.3066485 [8] ZHANG Yiling, WANG Hao, YANG Yan, et al. Deep matrix factorization with knowledge transfer for lifelong clustering and semi-supervised clustering[J]. Information Sciences, 2021, 570: 795–814. doi: 10.1016/j.ins.2021.04.067 [9] 金广智, 石林锁, 崔智高, 等. 结合GLCM与三阶张量建模的在线目标跟踪[J]. 电子与信息学报, 2016, 38(7): 1609–1615. doi: 10.11999/JEIT151108JIN Guangzhi, SHI Linsuo, CUI Zhigao, et al. Online object tracking based on gray-level co-occurrence matrix and third-order tensor[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1609–1615. doi: 10.11999/JEIT151108 [10] 张斌, 廖仁杰. 基于CNN与LSTM相结合的恶意域名检测模型[J]. 电子与信息学报, 2021, 43(10): 2944–2951. doi: 10.11999/JEIT200679ZHANG Bin and LIAO Renjie. Malicious domain name detection model based on CNN and LSTM[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2944–2951. doi: 10.11999/JEIT200679 [11] ZHANG Jianfeng, ZHU Yan, ZHANG Xiaoping, et al. Developing a long short-term memory (LSTM) based model for predicting water table depth in agricultural areas[J]. Journal of Hydrology, 2018, 561: 918–929. doi: 10.1016/j.jhydrol.2018.04.065 [12] 陈宁, 林霞, 桂卫华, 等. 基于CCHS的浮选泡沫图像纹理特征提取[J]. 中南大学学报:自然科学版, 2013, 44(11): 4506–4512.CHEN Ning, LIN Xia, GUI Weihua, et al. Flotation froth image texture extraction based on CCHS[J]. Journal of Central South University:Science and Technology, 2013, 44(11): 4506–4512. [13] 王俊, 曹俊兴, 刘哲哿, 等. 基于长短期记忆网络的钻前测井曲线预测方法[J]. 成都理工大学学报:自然科学版, 2020, 47(2): 227–236. doi: 10.3969/j.issn.1671-9727.2020.02.11WANG Jun, CAO Junxing, LIU Zhege, et al. Method of well logging prediction prior to well drilling based on long short-term memory recurrent neural network[J]. Journal of Chengdu University of Technology:Science &Technology Edition, 2020, 47(2): 227–236. doi: 10.3969/j.issn.1671-9727.2020.02.11 [14] HAN Jian, LU Chenghui, CAO Zhimin, et al. Integration of deep neural networks and ensemble learning machines for missing well logs estimation[J]. Flow Measurement and Instrumentation, 2020, 73: 101748. doi: 10.1016/j.flowmeasinst.2020.101748 [15] ALAIFARI R and WELLERSHOFF M. Uniqueness of STFT phase retrieval for bandlimited functions[J]. Applied and Computational Harmonic Analysis, 2021, 50: 34–48. doi: 10.1016/j.acha.2020.08.003 [16] JALAYER M, ORSENIGO C, and VERCELLIS C. Fault detection and diagnosis for rotating machinery: A model based on convolutional LSTM, fast Fourier and continuous wavelet transforms[J]. Computers in Industry, 2021, 125: 103378. doi: 10.1016/j.compind.2020.103378 -





 下载:
下载:




 下载:
下载:
