Memory Circuit Design, Implementation and Analysis Based on Memristor Full-function Pavlov Associative
-
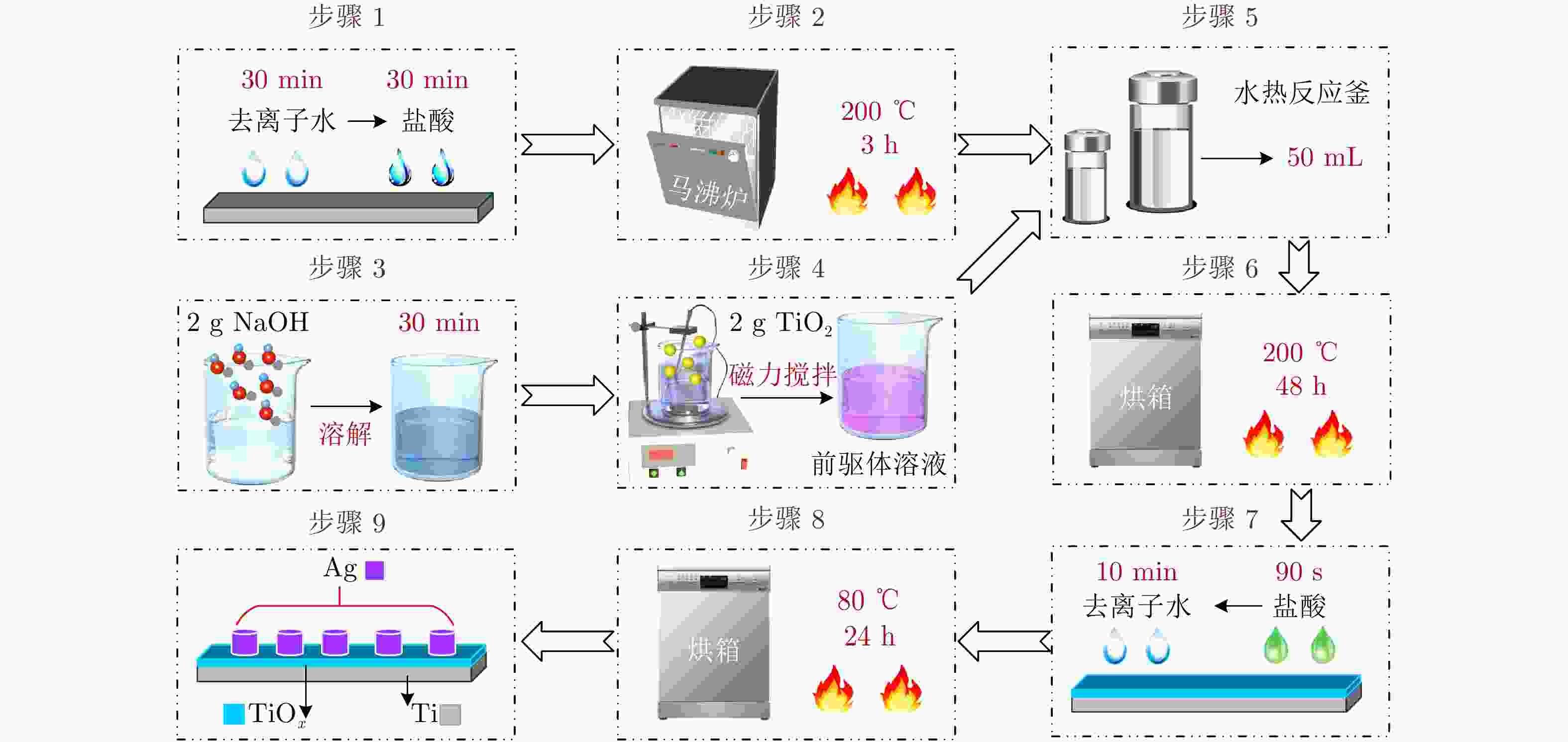
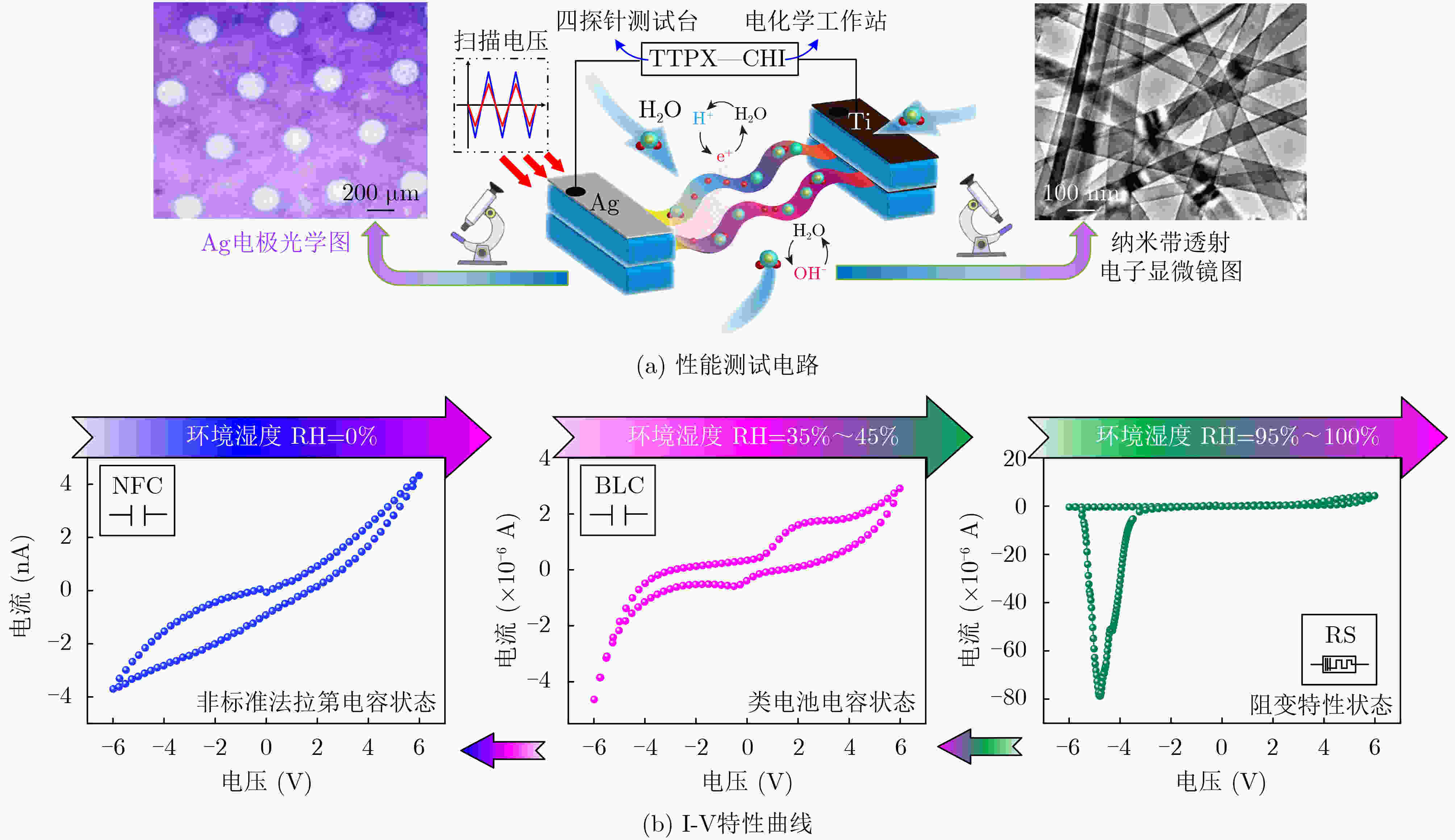
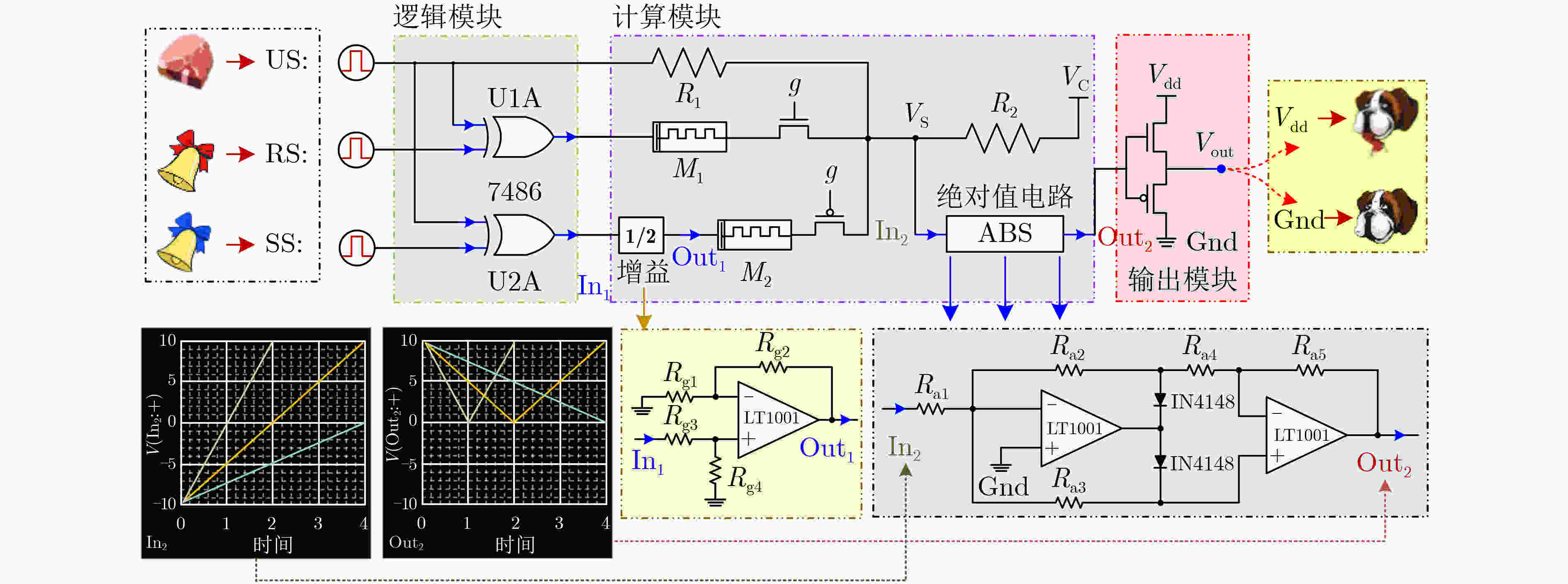
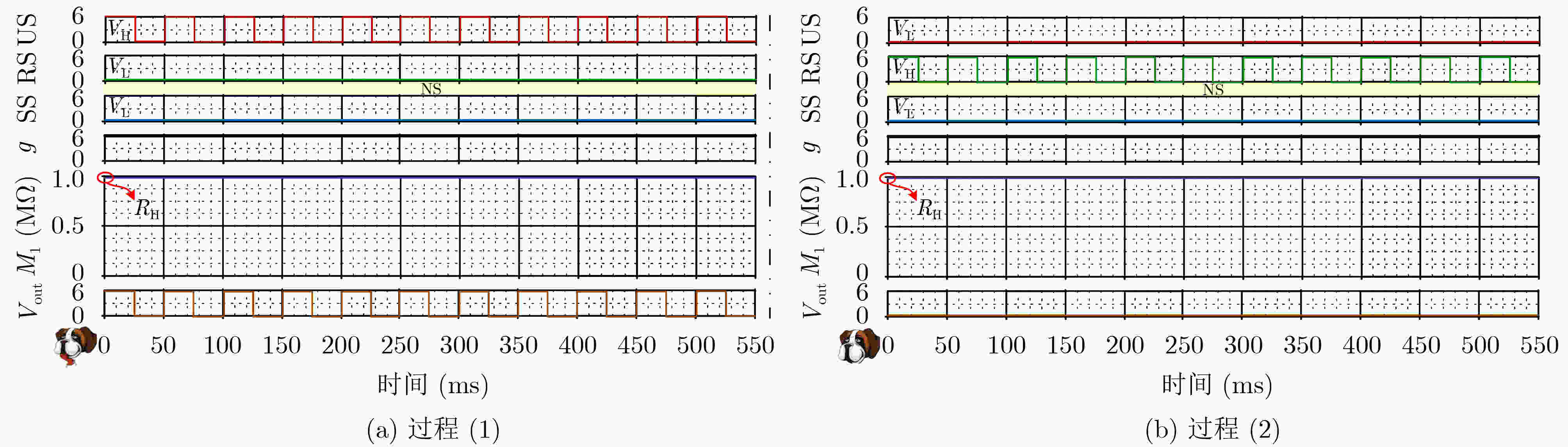
摘要: 联想记忆是一种描述生物学习和遗忘过程的重要机制,对构建神经形态计算系统和模拟类脑功能有重要的意义,设计并实现联想记忆电路成为人工神经网络领域内的研究热点。巴甫洛夫条件反射实验作为联想记忆的经典案例之一,其硬件电路的实现方案仍然存在电路设计复杂、功能不完善以及过程描述不清晰等问题。基于此,该文融合经典的条件反射理论和纳米科学技术,提出一种基于忆阻的全功能巴甫洛夫联想记忆电路。首先,基于水热合成法和磁控溅射法制备了Ag/TiOx nanobelt/Ti结构的忆阻器,通过电化学工作站、四探针测试台和透射电子显微镜联合完成相应的性能测试;接着,利用测试得到的电化学数据,构建了Ag/TiOx nanobelt/Ti忆阻器的数学模型和SPICE电路模型,并通过客观评价验证模型的精确度;进一步,基于提出的Ag/TiOx nanobelt/Ti忆阻器模型,设计了一种全功能巴甫洛夫联想记忆电路,通过电路描述和功能分析,论述了该电路能够正确模拟巴甫洛夫实验中2类学习过程和3类遗忘过程;最后,通过一系列计算机仿真和分析,验证了所提方案的正确性和有效性。Abstract: Associative memory is an important mechanism describing biological learning process and forgetting process, which is of great significance for constructing neuromorphic computing systems, as well as simulating brain-like functions. As a result, the design and implementation of associative memory circuit has become a research hotspot in the field of artificial neural networks. Pavlov conditioning experiment, as one of the classic cases of associative memory, its hardware implementation still suffers from some limitations such as complex circuit configuration, imperfect function and unclear process description. Based on this, a memory circuit is proposed based on memristor full-fuction pavlov associative in this paper, which combines the classical conditioned reflection theory and nano science and technology. Firstly, the Ag/TiOx nanobelt/Ti memristor is prepared using hydrothermal synthesis method and magnetron sputtering method, and its performance testing is conducted jointly by electrochemical workstation, four-probe test bench, and transmission electron microscope. Then, the mathematical model and SPICE circuit model of the Ag/TiOx nanobelt/Ti memristor are built up respectively, based on the electrochemical data derived from the performance testing, and the model accuracy is verified by objective evaluation. Furthermore, the proposed Ag/TiOx nanobelt/Ti memristor model is applied to the implementation of a full-function Pavlovian associative memory circuit. The specific circuit description and function analysis illustrate that this circuit is able to simulate two kinds of learning process and three kinds of forgetting process in Pavlov experiment. Finally, a series of computer simulation and analysis are carried out, which verifies the validity and effectiveness of the entire scheme.
-
Key words:
- Memristor /
- Associative memory /
- Pavlov conditioning /
- Circuit implementation /
- Performance testing
-
表 1 巴甫洛夫联想记忆电路的对比信息汇总
表 2 Ag/TiOx nanobelt/Ti忆阻器SPICE模型子电路描述
* Ag/TiOx nanobelt/Ti memristor .SUBCKT IJBCMEM Plus Minus PARAMS: +kL=-6 AlphaL=2 aL=-1 wL=2 a1=0.22 b1=-0.38 c1=0.166 d1=9.96E-05 kH=3E-3 AlphaH=4 aH=-1 wH=1 +a2=0.22 b2=-10 b2=-10 c2=8.15 d2=3E-08 Vth1=0 Vth2=0 ****************Differential equation mode*************** Gx 0 x value={F(V(x),V(Plus,Minus),aL,aH,wL,wH,kL,kH,AlphaL,AlphaH)} Cx x 0 1 IC={0} Raux x 0 1T ***********************Ohms law*********************** Gm Plus Minus value={IVRel(V(x),V(Plus,Minus),a1,a2,b1,b2,c1,c2,d1,d2)} ***********************Functions*********************** .func f1(x,v,kL,AlphaL,aL,wL)={kL*v^AlphaL*exp(-exp(aL*x+wL))} .func f2(x,v,kH,AlphaH,aH,wH)={kH*v^AlphaH*exp(-exp(aH*x+wH))} .func f3(x,v,a1,b1,c1,d1)={a1*x*exp(b1*x^3+c1)*sinh(d1*(v)^3)} .func f4(x,v,a2,b2,c2,d2)={a2*x*exp(b2*x^3+c2)*sinh(d2*(v)^3)} .func F(x,v,aL,aH,wL,wH,kL,kH,AlphaL,AlphaH)={if(v<Vth1,f1(x,v,kL,AlphaL,aL,wL), +if(v>Vth2,f2(x,v,kH,AlphaH,aH,wH),0))} .func IVRel(x,v,a1,a2,b1,b2,c1,c2,d1,d2)={if(v<Vth1,f3(x,v,a1,b1,c1,d1),if(v>Vth2,f4(x,v,a2,b2,c2,d2),0))} ENDS Ag/TiOx nanobelt/Ti memristor 表 3 巴甫洛夫联想记忆信息汇总
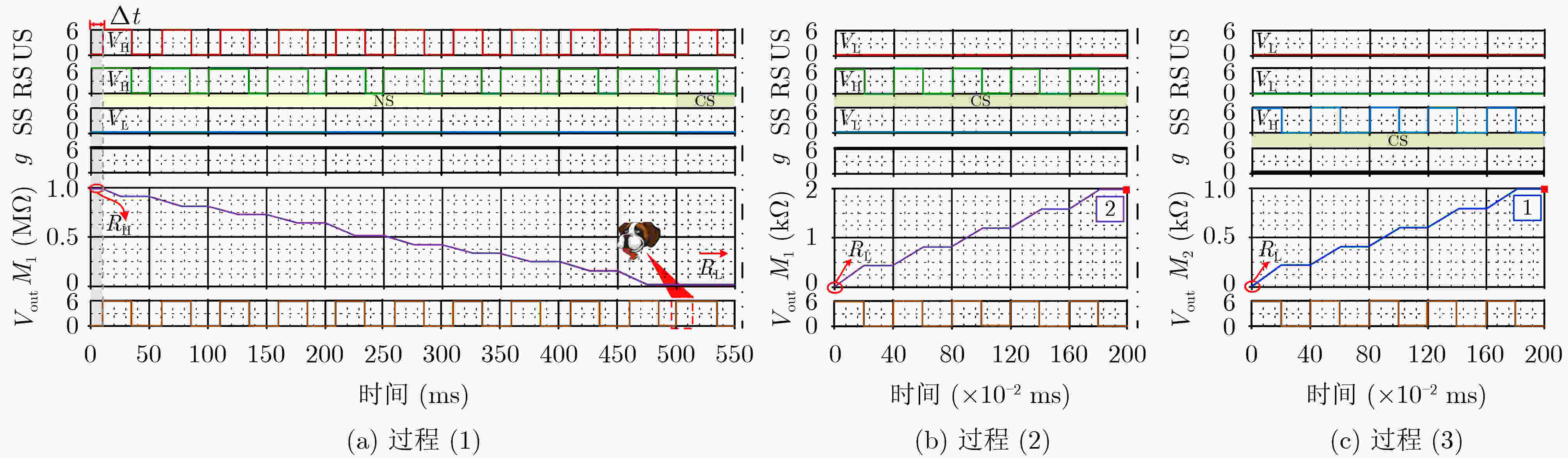
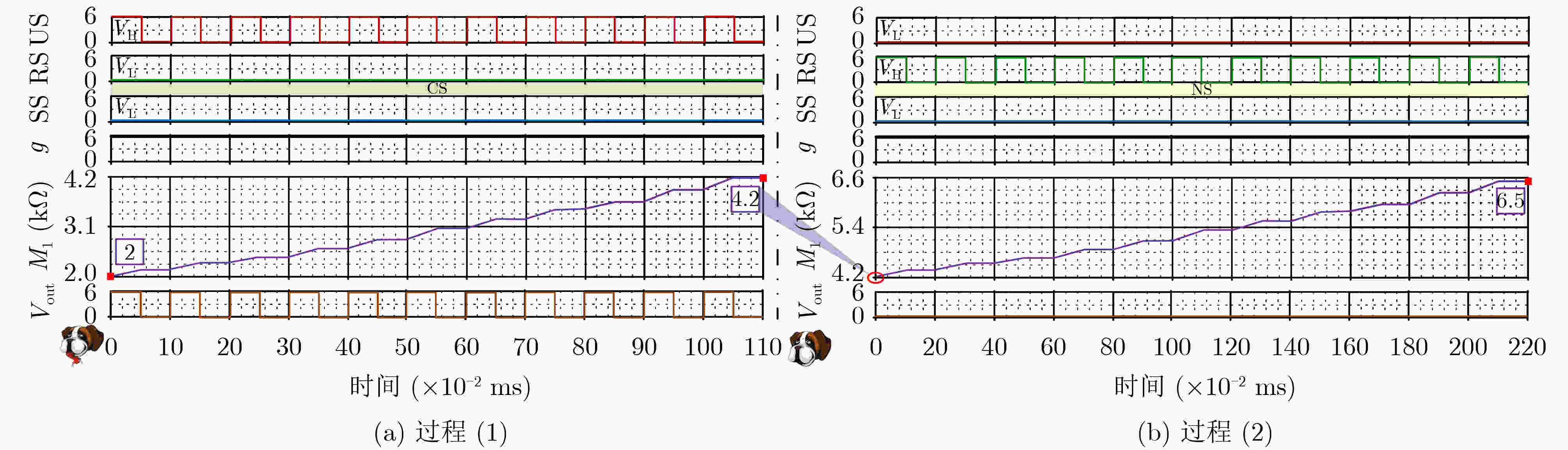
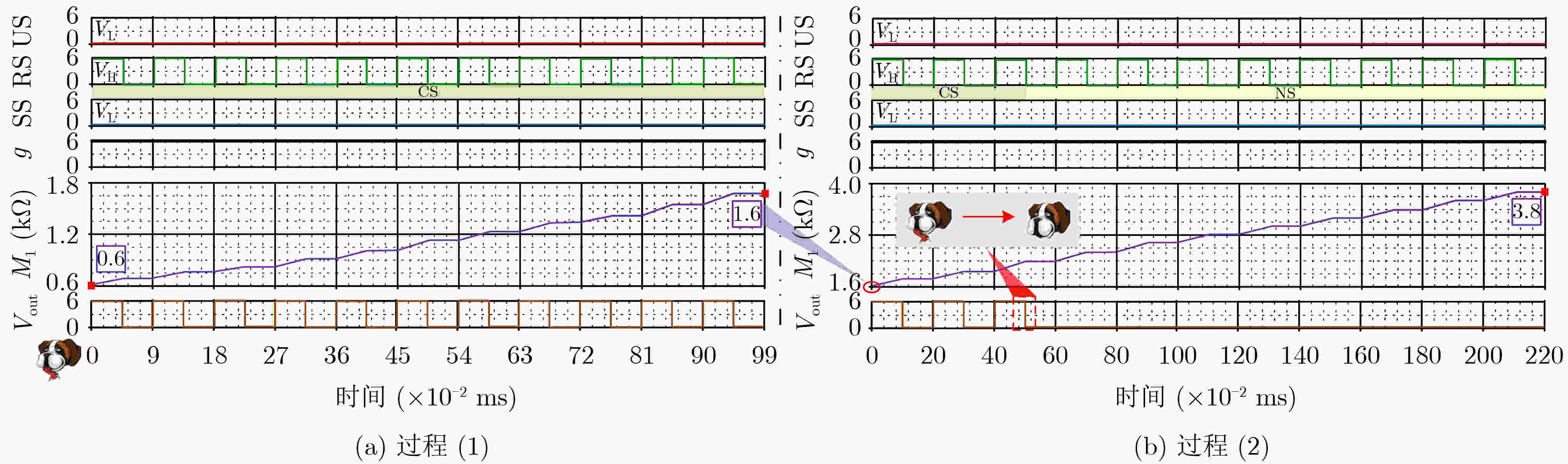
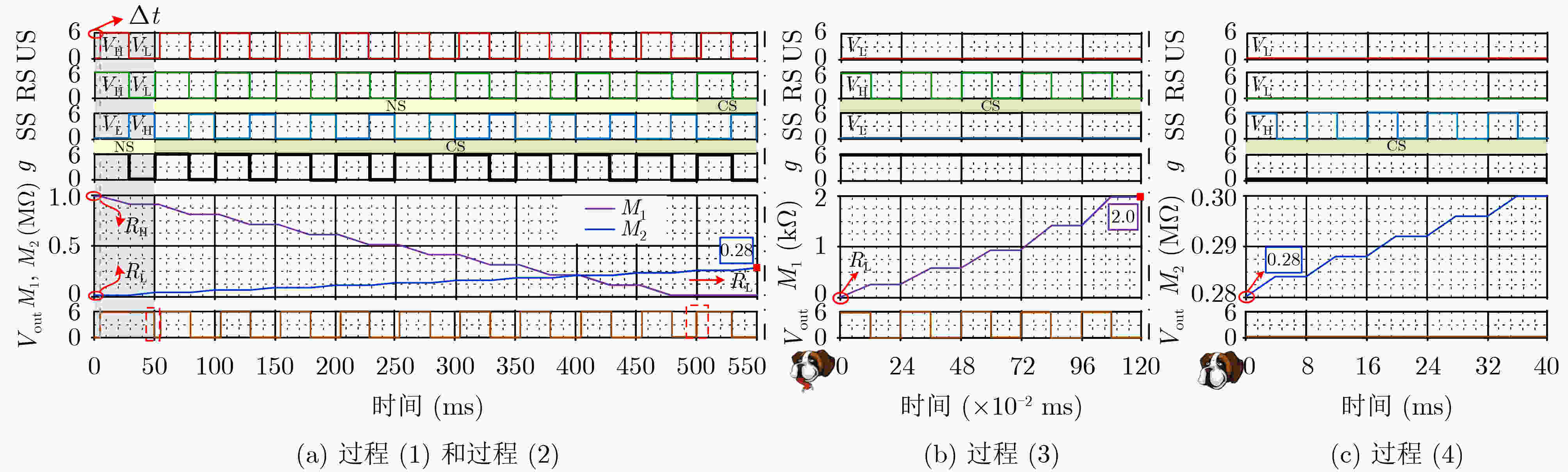
学习过程 遗忘过程 






/ / / 
-
[1] ZYARAH A M, GOMEZ K, and KUDITHIPUDI D. Neuromorphic system for spatial and temporal information processing[J]. IEEE Transactions on Computers, 2020, 69(8): 1099–1112. [2] RYU J H, KIM B, HUSSAIN F, et al. Bio-inspired synaptic functions from a transparent zinc-tin-oxide-based memristor for neuromorphic engineering[J]. Applied Surface Science, 2021, 544: 148796. doi: 10.1016/j.apsusc.2020.148796 [3] 董哲康, 杜晨杰, 林辉品, 等. 基于多通道忆阻脉冲耦合神经网络的多帧图像超分辨率重建算法[J]. 电子与信息学报, 2020, 42(4): 835–843. doi: 10.11999/JEIT190868DONG Zhekang, DU Chenjie, LIN Huipin, et al. Multi-channel memristive pulse coupled neural network based multi-frame images super-resolution reconstruction algorithm[J]. Journal of Electronics &Information Technology, 2020, 42(4): 835–843. doi: 10.11999/JEIT190868 [4] DONG Zhekang, LAI C S, ZHANG Zhaowei, et al. Neuromorphic extreme learning machines with bimodal memristive synapses[J]. Neurocomputing, 2021, 453: 38–49. doi: 10.1016/j.neucom.2021.04.049 [5] DONG Zhekang, QI Donglian, HE Yufei, et al. Easily cascaded memristor-CMOS hybrid circuit for high-efficiency boolean logic implementation[J]. International Journal of Bifurcation and Chaos, 2018, 28(12): 1850149. doi: 10.1142/S0218127418501493 [6] YANG Zijia and WANG Xiaoping. Memristor-based BAM circuit implementation for image associative memory and filling-in[J]. Neural Computing and Applications, 2021, 33(13): 7929–7942. doi: 10.1007/s00521-020-05538-7 [7] ZIEGLER M, SONI R, PATELCZYK T, et al. An electronic version of Pavlov’s dog[J]. Advanced Functional Materials, 2012, 22(13): 2744–2749. doi: 10.1002/adfm.201200244 [8] BICHLER O, ZHAO W, ALIBART F, et al. Pavlov’s dog associative learning demonstrated on synaptic-like organic transistors[J]. Neural Computation, 2013, 25(2): 549–566. doi: 10.1162/NECO_a_00377 [9] HU S G, LIU Y, LIU Z, et al. Synaptic long-term potentiation realized in Pavlov’s dog model based on a NiOx-based memristor[J]. Journal of Applied Physics, 2014, 116(21): 214502. doi: 10.1063/1.4902515 [10] LI Yi, XU Lei, ZHONG Yingpeng, et al. Associative learning with temporal contiguity in a memristive circuit for large-scale neuromorphic networks[J]. Advanced Electronic Materials, 2015, 1(8): 1500125. doi: 10.1002/aelm.201500125 [11] YU Fei, ZHU Liqiang, XIAO Hui, et al. Restickable oxide neuromorphic transistors with spike-timing-dependent plasticity and Pavlovian associative learning activities[J]. Advanced Functional Materials, 2018, 28(44): 1804025. doi: 10.1002/adfm.201804025 [12] 徐威, 王钰琪, 李岳峰, 等. 新型忆阻器神经形态电路的设计及其在条件反射行为中的应用[J]. 物理学报, 2019, 68(23): 238501. doi: 10.7498/aps.68.20191023XU Wei, WANG Yuqi, LI Yuefeng, et al. Design of novel memristor-based neuromorphic circuit and its application in classical conditioning[J]. Acta Physica Sinica, 2019, 68(23): 238501. doi: 10.7498/aps.68.20191023 [13] PEI Yifei, ZHOU Zhenyu, CHEN A P, et al. A carbon-based memristor design for associative learning activities and neuromorphic computing[J]. Nanoscale, 2020, 12(25): 13531–13539. doi: 10.1039/D0NR02894K [14] PERSHIN Y V and DI VENTRA M. Experimental demonstration of associative memory with memristive neural networks[J]. Neural Networks, 2010, 23(7): 881–886. doi: 10.1016/j.neunet.2010.05.001 [15] CHEN Ling, LI Chuandong, WANG Xin, et al. Associate learning and correcting in a memristive neural network[J]. Neural Computing and Applications, 2013, 22(6): 1071–1076. doi: 10.1007/s00521-012-0868-7 [16] WANG Lidan, LI Huifang, DUAN Shukai, et al. Pavlov associative memory in a memristive neural network and its circuit implementation[J]. Neurocomputing, 2016, 171: 23–29. doi: 10.1016/j.neucom.2015.05.078 [17] YANG Le, ZENG Zhigang, and WEN Shiping. A full-function Pavlov associative memory implementation with memristance changing circuit[J]. Neurocomputing, 2018, 272: 513–519. doi: 10.1016/j.neucom.2017.07.020 [18] SHANG Meijia and WANG Xiaoping. A memristor-based circuit design for generalization and differentiation on Pavlov associative memory[J]. Neurocomputing, 2020, 389: 18–26. doi: 10.1016/j.neucom.2019.12.106 [19] SUN Junwei, HAN Juntao, LIU Peng, et al. Memristor-based neural network circuit of Pavlov associative memory with dual mode switching[J]. AEU-International Journal of Electronics and Communications, 2021, 129: 153552. doi: 10.1016/j.aeue.2020.153552 [20] LO H Y, YANG C Y, HUANG G M, et al. Observing topotactic phase transformation and resistive switching behaviors in low power SrCoOx memristor[J]. Nano Energy, 2020, 72: 104683. doi: 10.1016/j.nanoen.2020.104683 [21] ZHOU Guangdong, REN Zhijun, SUN Bai, et al. Capacitive effect: An original of the resistive switching memory[J]. Nano Energy, 2020, 68: 104386. doi: 10.1016/j.nanoen.2019.104386 [22] ZHOU Guangdong, REN Zhijun, WANG Lidan, et al. Resistive switching memory integrated with amorphous carbon-based nanogenerators for self-powered device[J]. Nano Energy, 2019, 63: 103793. doi: 10.1016/j.nanoen.2019.05.079 [23] YU L S, LIU Q Z, XING Q J, et al. The role of the tunneling component in the current-voltage characteristics of metal-GaN Schottky diodes[J]. Journal of Applied Physics, 1998, 84(4): 2099–2104. doi: 10.1063/1.368270 [24] AFIFI A, AYATOLLAHI A, and RAISSI F. STDP implementation using memristive nanodevice in CMOS-Nano neuromorphic networks[J]. IEICE Electronics Express, 2009, 6(3): 148–153. doi: 10.1587/elex.6.148 [25] LI Junrui, DONG Zhekang, LUO Li, et al. A novel versatile window function for memristor model with application in spiking neural network[J]. Neurocomputing, 2020, 405: 239–246. doi: 10.1016/j.neucom.2020.04.111 [26] HUTTER F, HOOS H H, and LEYTON-BROWN K. Sequential model-based optimization for general algorithm configuration[C]. The 5th International Conference on Learning and Intelligent Optimization, Rome, Italy, 2011: 507–523. [27] LIN G F and CHEN L H. A non-linear rainfall-runoff model using radial basis function network[J]. Journal of Hydrology, 2004, 289(1/4): 1–8. [28] RESCORLA R A. Pavlovian conditioning: It’s not what you think it is[J]. American Psychologist, 1988, 43(3): 151–160. doi: 10.1037/0003-066X.43.3.151 [29] RESCORLA R A. Behavioral studies of Pavlovian conditioning[J]. Annual Review of Neuroscience, 1988, 11: 329–352. doi: 10.1146/annurev.ne.11.030188.001553 [30] ALSAEED N H. Wish you were here: A psychological analysis using Atkinson-Shiffrin memory mode[J]. Journal of Literature and Art Studies, 2017, 6(5): 521–527. [31] BARKER R W J and HART B L. Precision absolute-value circuit technique[J]. International Journal of Electronics, 1989, 66(3): 445–448. doi: 10.1080/00207218908925401 -





 下载:
下载:


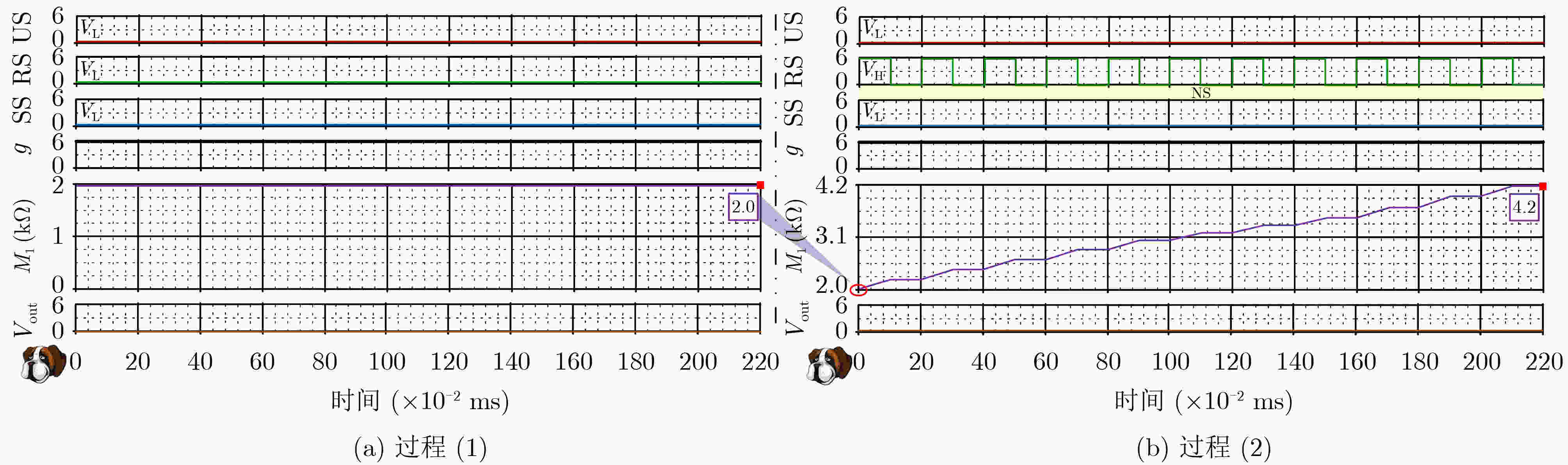


 下载:
下载:
