Two-dimensional Underwent Synthetic Aperture Radar Imaging Based on Iterative Proximal Projection
-
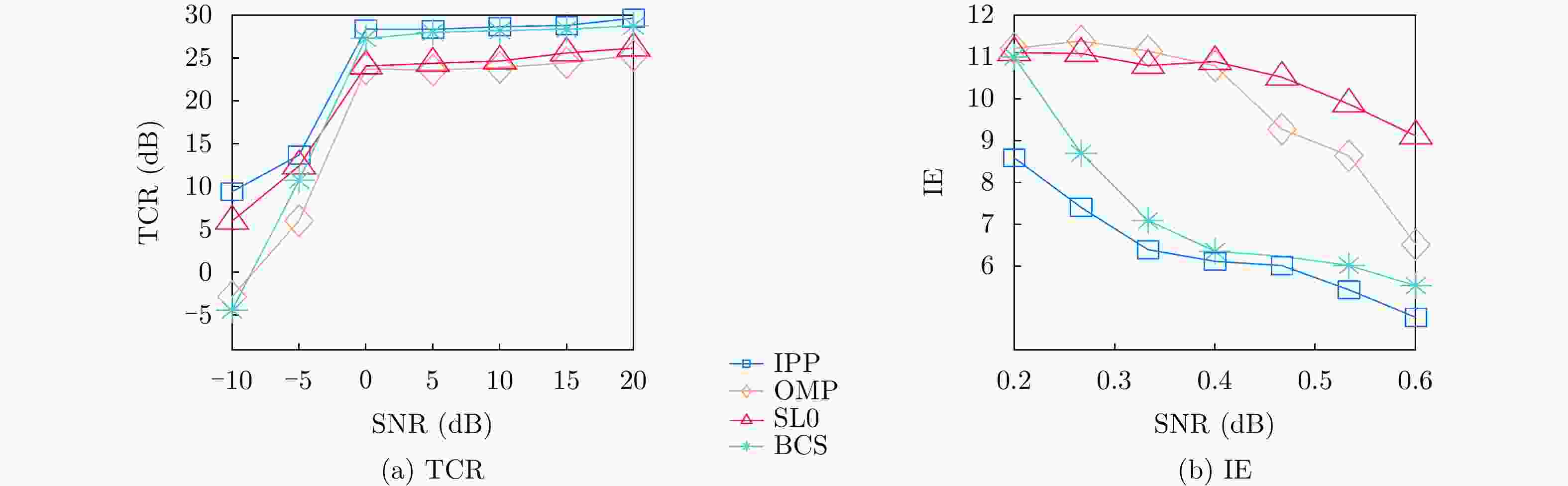
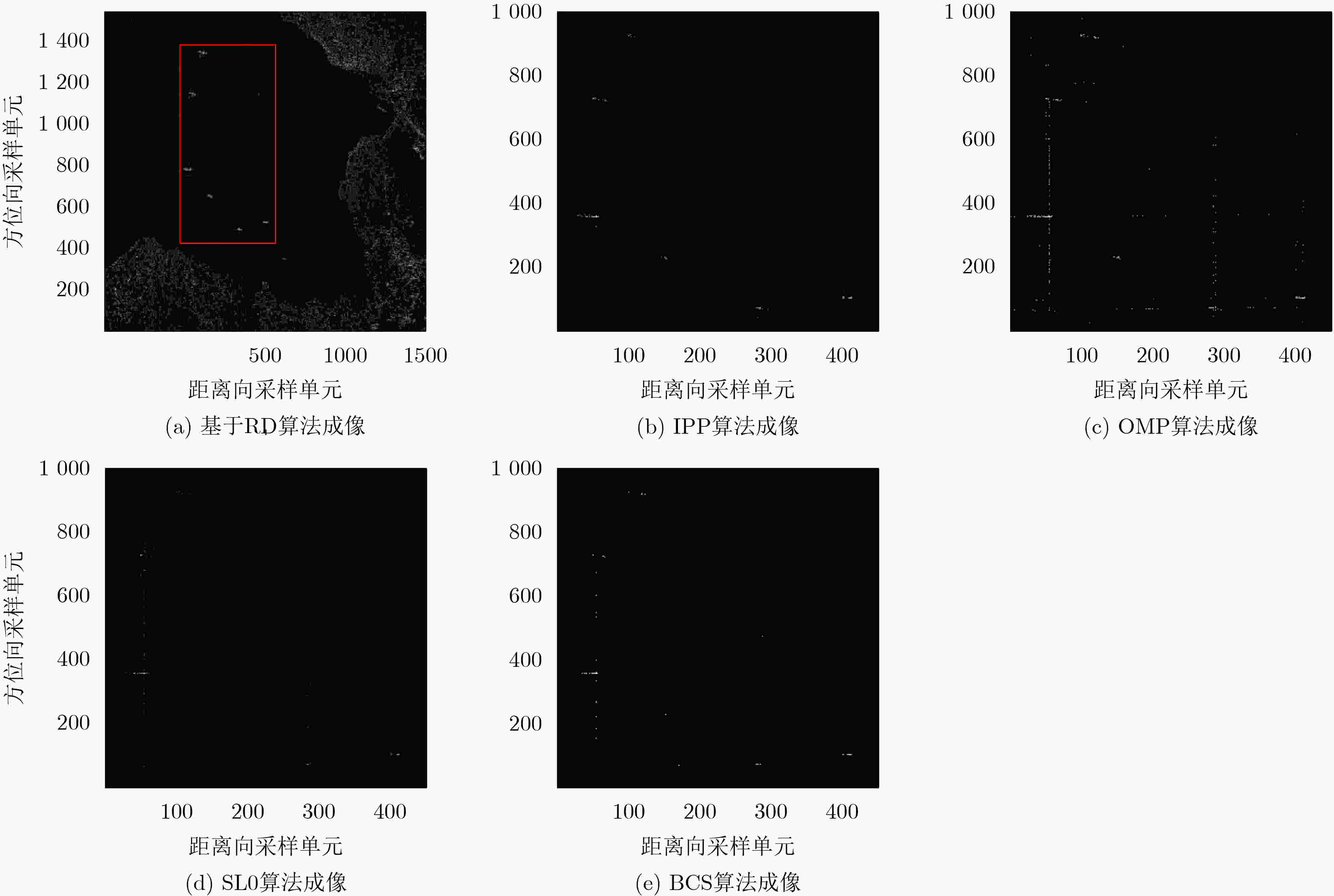
摘要: 合成孔径成像雷达(SAR)具有数据量大、采样率高等特点，针对传统压缩感知(CS)的SAR成像存在精度低及抗噪性能差的问题，该文提出一种基于迭代近端投影(IPP)的2维欠采样合成孔径雷达成像重建方法。即通过对雷达回波构建为距离频域-方位多普勒域的2维稀疏表示模型，在此基础上将成像问题转化为距离向和方位向压缩感知稀疏重构问题，利用迭代近端投影算法的函数优化模型来表示合成孔径雷达成像中的稀疏表示，最后采用平滑削边绝对偏离(SCAD)罚函数获得近端算子以求解该模型并进行成像。仿真与实测数据处理结果表明，所提方法成像效果更好。
-
关键词:
- SAR成像 /
- 压缩感知 /
- 迭代近端投影 /
- 平滑削边绝对偏离罚函数
Abstract: Synthetic Aperture Radar (SAR) imaging has a large amount of data volume, high sampling rate, and the problem of SAR imaging precision in traditional Compression Sensing (CS) is low, and there is a problem of poor anti-noise performance. A method of reconstruction method of two - dimensional sampling synthetic aperture rada based on Iterative Proximal Projection (IPP) is proposed. The radar echo is constructed as a two-dimensional sparse representation model in the range frequency-domain-azimuth Doppler region. On this basis, the two-dimensional imaging problem is transformed into the range and azimuth compression sensing sparse reconstruction. The function optimization model of the iterative proximal projection algorithm is used to represent the sparse representation of the synthetic aperture thunder imaging, and the proximal operator is finally obtained with the Smoothly Clipped Absolute Deviation (SCAD) penalty function to solve the model and to image. Simulation and measured data processing results show that the method of imaging is better. -
1. 引言
合成孔径雷达(Synthetic Aperture Radar , SAR)是最早提出并投入实用的成像雷达。合成孔径雷达可实现全天时、全天候的区域监测成像，且对植被等介质具有穿透能力，在灾害评估、环境监测和军事等领域得到了广泛的应用[1-3]。
由雷达分辨率理论和奈奎斯特采样定理可知，合成孔径雷达系统性能的提高通常伴随着采样数据量的显著增加，这给系统设计和实现带来困难。近年来，随着压缩感知[4]和相关理论的发展，稀疏信号处理在SAR成像中得到广泛应用，这表明当回波信号具有稀疏性或可压缩性时，便能够以远低于奈奎斯特的采样频率，用较少的观测数据高概率地恢复出原信号。现有的压缩感知SAR成像模型中，大致分为两大类，其一，单独考虑距离向和方位向的稀疏模型，然后与匹配滤波相结合进行成像。例如文献[5]仅在距离向实现了压缩感知技术，文献[6]仅在方位向实现了压缩感知技术，上述方法都可以实现SAR成像，但也存在一些问题。首先，仍然需要处理较大的数据量且没有充分利用空间的稀疏性；其次，成像过程中用到的匹配滤波方式导致很大的局限性。其二，在距离向和方位向同时构建压缩感知模型进行求解[7-9]，其中文献[7]将接收到的雷达回波和2维后向散射系数矩阵叠加成非常大的列向量，然后进行方位向距离向压缩感知处理，虽然比仅对距离向和方位向处理更进一步减少了采样数据量，但求解过程需要对大的列向量进行处理，大幅增加大数据运算量与信号的重构时间。针对出现的问题，文献[8,9]将接收到的回波与后向散射系数保持为2维矩阵，而不是堆叠成向量，因此可以在降低采样率的同时很好地重建目标信号。不管是求解第1类成像模型还是第2类成像模型，都需要用到重构算法，最终目的都是解决l0范数最小化问题。传统的压缩感知重构算法包括凸优化算法、贪婪算法和统计优化算法3大类，例如文献[10]实现了基于随机孔径贝叶斯压缩感知理论的高分辨合成孔径雷达成像，这里用到了统计优化类算法，文献[11]将隶属于贪婪算法类的正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法应用到合成孔径雷达成像中，文献[12]将求解凸优化问题的快速迭代收缩算法(Fast Iterative Shrinkage Thresholding Algorithm, FISTA)应用到压缩感知ISAR成像的过程中。另有一些学者将非凸函数族中的平滑l0算法应用到合成孔径雷达方位向稀疏模型求解过程中。但这些重构算法都存在重构精度不高、抗噪性能差等问题。
针对上述问题，本文在文献[8,9]构建的压缩感知SAR成像模型的基础上，将非凸非平滑优化算法引入到压缩感知SAR成像模型的求解问题中，提出一种基于迭代近端投影的2维欠采样合成孔径雷达成像重建算法。首先将压缩感知SAR成像模型转化为近端函数[13,14]稀疏信号模型，然后采用SCAD判罚函数[15]来进一步求解该模型，进而重构出图像。仿真与实测数据处理结果表明，本文方法具有很好的重构性能，具有较好的工程应用前景。
2. SAR回波信号2维稀疏表示模型
图1为SAR成像几何模型，假设雷达平台沿
y 轴以恒定的速度v 前行，若雷达发射线性调频(Linearly Frequency Modulated, LFM)信号，则理想点目标P(x,y) 的基带回波为s(tr,ta;r)=∬Dg(x,y)aa(ta)ar(tr−2R(ta;r)c)⋅exp[jπγ(tr−2R(ta;r)c)2]⋅exp[−j4πλR(ta;r)]dxdy (1) 其中，
D={(x,y)|xmin ,R({t_{\text{a}}};r) 为{t_{\text{a}}} 时刻雷达与目标间的距离，其表达式为R({t_{\rm{a}}};r){\text{ = }}\sqrt {{r^2} + {v^2} \cdot {{({t_{\rm{a}}} - {t_{{{\rm{a}}_0}}})}^2}} \approx r + \frac{{{v^2}}}{{2r}}{\left({t_{\rm{a}}} - {t_{{{\rm{a}}_0}}}\right)^2} (2) 其中，
{t_{\rm{r}}} 和{t_{\rm{a}}} 分别为距离向快时间和方位向慢时间；r 为点目标P(x,y) 到雷达航线的垂直距离；{\boldsymbol{g}}\left( {x,y} \right) 为目标的后向散射系数矩阵；a{}_{\rm{a}}( \cdot ) 为方位向窗函数；{a_{\rm{r}}}({t_{\rm{r}}}) = {\rm{rect}}\left(\dfrac{{{t_{\rm{r}}}}}{{{T_{\rm{p}}}}}\right) 为发射信号包络，{T_{\rm{p}}} 为脉冲持续时间；c 为光速；\gamma 为发射的LFM信号的线性调频率；\lambda 为波长。根据文献[8]和文献[9]知，理想点目标的回波经采样后可以表示为{\boldsymbol{S}} = {{\boldsymbol{\varPhi}} _{\rm{r}}}{\boldsymbol{G}}{{\boldsymbol{\varPhi}} _{\rm{a}}} (3) 其中，
{\boldsymbol{S}} \in {\mathbb{C}^{M \times N}} 表示均匀采样回波信号；{\boldsymbol{G}} \in {\mathbb{C}^{M \times N}} 表示观测场景目标点的后向散射矩阵；矩阵{{\boldsymbol{\varPhi}} _{\text{r}}} \in {\mathbb{C}^{M \times M}} 为距离向的卷积矩阵，其列是距离向参考函数的共轭与快时间域中采样数的卷积，其中距离向参考函数可以表示为{s_{\rm{r}}}({t_{\rm{r}}}) = {a_{\rm{r}}}\left( {{t_{\rm{r}}}} \right)\exp ({\rm{j}}\pi \gamma t_r^2) ；矩阵{{\boldsymbol{\varPhi}} _{\text{a}}} \in {\mathbb{C}^{N \times N}} 为方位向的卷积矩阵，其行是方位向参考函数的共轭与慢时间域中采样数的卷积，其中方位向参考函数可以表示为{s_{\rm{a}}}({t_{\rm{a}}}) = {a_{\rm{a}}}\left( {{t_{\rm{a}}}} \right)\exp \left( {{\rm{j}}\pi {k_{\rm{a}}}t_{\rm{a}}^2} \right) ，其中{k_{\rm{a}}} = \dfrac{{2{v^2}r}}{\lambda } 为多普勒调频率；\mathbb{C} 表示复数域；M 为距离向采样点数；N 为方位向采样点数。对飞机、桥梁等具有空域稀疏性的场景，首先，构建稀疏随机测量矩阵来减少2维采样量，随机测量矩阵构建方式为随机选取方位向和距离向部分采样点信号，如图2所示，其中灰色部分代表采样点信号。此时均匀采样回波信号
{\boldsymbol{S}} \in {\mathbb{C}^{M \times N}} 变为随机采样的回波信号{{\boldsymbol{S}}_{2{\rm{CS}}}} \in {\mathbb{C}^{P \times Q}} ，P\left( {P \le M} \right) 为距离向随机采样点数，Q\left( {Q \le N} \right) 为方位向随机采样点数。与此同时，距离向卷积矩阵{{\boldsymbol{\varPhi}} _{\rm{r}}} 变为{{\boldsymbol{\varPhi}} _{{\rm{RCS}}}} \in {\mathbb{C}^{P \times M}} ，方位向卷积矩阵{{\boldsymbol{\varPhi}} _{\rm{a}}} 变为{{\boldsymbol{\varPhi}} _{{\rm{ACS}}}} \in {\mathbb{C}^{N \times Q}} ，通过上述整理可得，2维随机降采样合成孔径雷达回波信号的欠定方程表示为{{\boldsymbol{S}}_{2{\rm{CS}}}}{\text{ = }}{{\boldsymbol{\varPhi}} _{{\rm{RCS}}}}{\boldsymbol{G}}{{\boldsymbol{\varPhi}} _{{\rm{ACS}}}} (4) 考虑到现实场景中加性噪声的影响，式(4)可以表示为
{{\boldsymbol{S}}_{2{\rm{ZCS}}}}{\text{ = }}{{\boldsymbol{\varPhi}} _{{\rm{RCS}}}}{\boldsymbol{G}}{{\boldsymbol{\varPhi}} _{{\rm{ACS}}}} + {{\boldsymbol{N}}_Z} (5) 其中，
{{\boldsymbol{S}}_{2{\rm{CS}}}} \in {\mathbb{C}^{P \times Q}},{{\boldsymbol{S}}_{2{\rm{ZCS}}}} \in {\mathbb{C}^{P \times Q}} 为随机采样的回波信号，{{\boldsymbol{\varPhi}} _{{\rm{RCS}}}} \in {\mathbb{C}^{P \times M}} 为距离维观测矩阵，{{\boldsymbol{\varPhi}} _{{\rm{ACS}}}} \in {\mathbb{C}^{N \times Q}} 为方位维观测矩阵，{\boldsymbol{G}} \in {\mathbb{C}^{M \times N}} 为待重构的目标图像，{{\boldsymbol{N}}_Z} \in {\mathbb{C}^{P \times Q}} 为复高斯白噪声信号。3. 基于迭代近端投影的合成孔径雷达成像方法
由上述章节描述可知，式(5)所表示的信号模型是2维卷积模型，它可以用两个连续的1维方程表示。首先，令
{\boldsymbol{X}} \in {\mathbb{C}^{M \times Q}} 作为方位维压缩数据。其表达式为{\boldsymbol{X}} = {\boldsymbol{G}}{{\boldsymbol{\varPhi}} _{{\rm{ACS}}}} (6) 则式(5)可以写为
{{\boldsymbol{S}}_{{\text{2ZCS}}}} = {{\boldsymbol{\varPhi}} _{{\rm{RCS}}}}{\boldsymbol{X}} + {{\boldsymbol{N}}_Z} (7) 式(6)表示方位向压缩感知模型，式(7)表示距离向压缩感知模型。
求解式(7)和式(6)的过程如下，首先，求解欠定方程式(7)得到距离向压缩后的信号，其次，将接收到的回波
{{\boldsymbol{S}}_{{\text{2ZCS}}}} 分解为列向量的形式，其表达式为{{\boldsymbol{S}}_{{\text{2ZCS}}}} = \left[ {{s_1},{s_2}, \cdots ,{s_Q}} \right] (8) 同时，
{\boldsymbol{X}} 也可以分解为列向量形式{\boldsymbol{X}} = \left[ {{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2}, \cdots ,{{\boldsymbol{x}}_Q}} \right] (9) 那么，式(7)可以表示为
{{\boldsymbol{s}}_q} = {{\boldsymbol{\varPhi}} _{{\rm{RCS}}}}{{\boldsymbol{x}}_q}{\kern 1pt} {\kern 1pt} + {{\boldsymbol{n}}_z},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} q = 1,2, \cdots ,Q (10) 其中，
{{\boldsymbol{s}}_q} \in {\mathbb{C}^P} ,{{\boldsymbol{x}}_q} \in {\mathbb{C}^M} ,{{\boldsymbol{n}}_z} \in {\mathbb{C}^P} ,Q 为方位向接收到的脉冲数。由于式(10)是欠定方程，其对应的优化问题为式(11)的拉格朗日(Lagrangian)形式[16]，\mathop {\min }\limits_{{x_q}} {\left\| {{x_q}} \right\|_0}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| {{s_q} - {{\boldsymbol{\varPhi}} _{{\rm{RCS}}}}{x_q}} \right\|_2} \le \xi (11) 其中，
{\left\| \cdot \right\|_0} 是l0范数，它表示向量{x_q} 中非零元素个数；{\Vert ·\Vert }_{2} 是l2范数；\xi 是一个与噪声水平有关的参数。众所周知，求解式(11)最小化问题是一个非凸非平滑优化问题，传统基于压缩感知的SAR成像方法是在一定条件下将l0范数最小化的非凸非平滑优化问题转化为凸或平滑问题进行求解，这会使稀疏模型不可避免地存在一定误差，进而导致SAR成像效果不佳。而本文将能够解决非凸非平滑问题的迭代近端投影的方法应用到合成孔径雷达成像中，具体过程如下。由文献[13,14]知，为求得式(10)稀疏解，可将其转化为近端函数优化问题，其稀疏信号表示模型为\mathop {\min }\limits_{{x_q},z} F\left( z \right) + {\delta _\mathcal{A}}_{_\varepsilon }\left( {{x_q}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z = {x_q}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (12) 其中，
F\left( \cdot \right) 是一个类似l0范数的非凸非平滑函数，z 是一个列向量的辅助变量，{\delta _{{\mathcal{A}_\varepsilon }}} 定义为{\mathcal{A}_\varepsilon } \triangleq \{ {x_q}:{\left\| {{s_q} - {{\boldsymbol{\varPhi}} _{{\rm{RCS}}}}{{\boldsymbol{x}}_q}} \right\|_2} \le \varepsilon \} 可行集的指示函数[13]，即{\delta _{{\mathcal{A}_\varepsilon }}} = \left\{ {\begin{array}{*{20}{c}} {0,}&{{{\boldsymbol{x}}_q} \in {\mathcal{A}_\varepsilon }} \\ { + \infty ,}&{{{\boldsymbol{x}}_q} \notin {\mathcal{A}_\varepsilon }} \end{array}} \right. (13) 其中，
{\Vert ·\Vert }_{2} 表示l2范数，式(12)的稀疏信号表示模型中引入惩罚函数方法，即\mathop {\min }\limits_{{x_q},z} F\left( z \right) + {\delta _\mathcal{A}}_{_\varepsilon }\left( {{x_q}} \right){\kern 1pt} + \frac{1}{{2\alpha }}\left\| {{x_q} - z} \right\|{\kern 1pt} _2^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (14) 其中，
\alpha > 0 为惩罚因子，通过交替最小化方法[17]解决式(14)所表示问题。表达式为\left. \begin{aligned} & {{{\boldsymbol{z}}_{k + 1}} = \arg {{\min }_z}\left\{ \alpha F\left( {\boldsymbol{z}} \right) + \frac{1}{2}\left\| {{\boldsymbol{z}} - {{\boldsymbol{x}}_{q,z}}} \right\|_2^2\right\} } \\ & {{{\boldsymbol{x}}_{q,z + 1}} = \arg {{\min }_{{x_q}}}\left\{ {\delta _{{\mathcal{A}_\varepsilon }}} + \frac{1}{2}\left\| {{{\boldsymbol{x}}_q} - {{\boldsymbol{z}}_{k + 1}}} \right\|_2^2\right\} } \end{aligned} \right\} (15) 根据文献[13]可知，式(15)可以进一步写为式(16)和式(17)
\left. \begin{aligned} \quad & {{{\boldsymbol{z}}_{k + 1}} = {\text{pro}}{{\text{x}}_{\alpha ,F}}({{\boldsymbol{x}}_{q,k}})} \\ & {{{\boldsymbol{x}}_{q,k + 1}} = {\text{pro}}{{\text{x}}_{{\delta _{{\mathcal{A}_\varepsilon }}}}}({{\boldsymbol{z}}_{k + 1}})} \end{aligned} \right\} (16) \begin{split} \qquad\;\;\quad {{\boldsymbol{x}}_{q,k + 1}} & = {\text{pro}}{{\text{x}}_{{\delta _{{\mathcal{A}_\varepsilon }}}}}\left( {{\text{pro}}{{\text{x}}_{\alpha ,F}}({{\boldsymbol{x}}_{q,k}})} \right) \\ & = {\mathcal{P}_{{\mathcal{A}_\varepsilon }}}({\text{pro}}{{\text{x}}_{\alpha ,F}}({{\boldsymbol{x}}_{q,k}})) \end{split} (17) 其中，
{\text{pro}}{{\text{x}}_{\alpha ,F}}({{\boldsymbol{x}}_{q,k}}) = \mathop {\arg \min }\limits_{{x_q}} \Bigr\{ \dfrac{1}{2}\left\| {{\boldsymbol{z}} - {{\boldsymbol{x}}_{q,k}}} \right\|_2^2 + \alpha F\left( {\boldsymbol{z}} \right)\Bigr\} 是F\left( z \right) 的近端算子，即求解{{\boldsymbol{x}}_{q,k}} 在满足约束条件下的最小的变量值z ，其核心思想就是将凸或非凸函数的优化问题转化为易求解的近端映射函数，从而实现近似解。{\mathcal{P}_{{\mathcal{A}_\varepsilon }}} 代表可行集{\mathcal{A}_\varepsilon } 的投影。此外，为了提高算法的性能和更好地解决非凸问题存在多个局部极小值的问题，本文利用外推步骤来改善算法性能，即\left. \begin{aligned} & {{{\bar {\boldsymbol{x}}}_{q,k}} = {{\boldsymbol{x}}_{q,k}} + \omega \left( {{{\boldsymbol{x}}_{q,k}} - {{\boldsymbol{x}}_{q,k - 1}}} \right)} \\ & {{{\bar {\boldsymbol{x}}}_{q,k + 1}} = {\mathcal{P}_{{\mathcal{A}_\varepsilon }}}\left( {{\text{pro}}{{\text{x}}_{\alpha ,F}}({{\bar {\boldsymbol{x}}}_{q,k}})} \right)} \end{aligned} \right\} (18) 其中，
\omega \ge 0 为权重常数。由文献[13]可知，非平滑函数的近端算子{\text{pro}}{{\text{x}}_{\alpha ,F}}({\bar {\boldsymbol{x}}_{q,k}}) 可由SCAD惩罚函数F\left( {{{\bar {\boldsymbol{x}}}_{q,k}}} \right) 产生相应的SCAD阈值函数T_{\lambda ,a}^{{\rm{scad}}} 来获得，该阈值函数可以进一步减小软、硬阈值收缩函数带来的偏差和促进解的稀疏性。因此，为进一步求得更优解，非平滑函数的近端算子{\text{pro}}{{\text{x}}_{\alpha ,F}}({\bar {\boldsymbol{x}}_{q,k}}) 可以表示为\begin{split} {\text{pro}}{{\text{x}}_{\alpha ,F}}({\bar x_{q,k}}) &= \mathop {\arg \min }\limits_{{{\bar x}_q}} \left\{ {\frac{1}{2}\left\| {{{\bar x}_q} - {{\bar x}_{q,k}}} \right\|_2^2 + \alpha F\left( {{{\bar x}_q}} \right)} \right\} \\ &= T_\lambda ^{{\rm{scad}}}\left( {{{\bar x}_q}} \right)\\[-10pt] \end{split} (19) 其中，惩罚函数
F\left( {{{\bar {\boldsymbol{x}}}_{q,k}}} \right) 的表达式为\begin{split} & F\left( {{{\bar {\boldsymbol{x}}}_{q,k}}} \right){\text{ = }}\\ & \left\{ \begin{aligned} & \lambda \left| {{{\bar {\boldsymbol{x}}}_{q,k}}} \right|,\qquad\qquad\qquad\qquad\qquad 0 \le \;\left| {{{\bar {\boldsymbol{x}}}_{q,k}}} \right| < \lambda \hfill \\ & - \frac{{\left( {{{\left| {{{\bar {\boldsymbol{x}}}_{q,k}}} \right|}^2} - 2a\lambda \left| {{{\bar {\boldsymbol{x}}}_{q,k}}} \right| + {\lambda ^2}} \right)}}{{2\left( {a - 1} \right)}},\; \lambda \le \;\left| {{{\bar {\boldsymbol{x}}}_{q,k}}} \right| < a\lambda \hfill \\ & \frac{{\left( {a + 1} \right){\lambda ^2}}}{2},\qquad\qquad\qquad\qquad\;\; \left| {{{\bar {\boldsymbol{x}}}_{q,k}}} \right| \ge a\lambda \end{aligned} \right. \end{split} (20) SCAD函数的近端映射为
\begin{split} & {T}_{\lambda ,a}^{{\rm{scad}}}\left({\overline{{\boldsymbol{x}}}}_{q}\right)=\\ & \left\{ \begin{aligned} & {\rm{sign}}\left({\overline{{\boldsymbol{x}}}}_{q}\right){\left(\left|{\overline{{\boldsymbol{x}}}}_{q}\right|-\lambda \right)}_+,\qquad \left|{\overline{{\boldsymbol{x}}}}_{q}\right|\le 2\lambda \\ & \frac{\left(a-1\right){\overline{{\boldsymbol{x}}}}_{q}-{\rm{sign}}\left({\overline{{\boldsymbol{x}}}}_{q}\right)a\lambda }{a-2},2\lambda < \left|{\overline{{\boldsymbol{x}}}}_{q}\right|\le a\lambda \\ & {\overline{{\boldsymbol{x}}}}_{q},\qquad \qquad \qquad \qquad \quad\;\; \left|{\overline{{\boldsymbol{x}}}}_{q}\right| > a\lambda \end{aligned}\right. \end{split} (21) 其中，
\lambda 为调整参数，a 为常量且a > 2 ，{\rm{sign}}\left( \cdot \right) 为符号函数，{\left(\beta \right)}_{\text{+}}\text{=}\mathrm{max}\left(\beta ，0\right) 。通过求解式(18)得到稀疏向量{\bar {\boldsymbol{x}}_q} ，至此，由{\bar{\boldsymbol{ x}}_q} 构成的{\boldsymbol{X}} 就是经过距离向压缩感知得到的1维距离像。然后，再对方位向压缩感知模型式(6)进行求解，为了更好地表述，将式(6)进行转置得{{\boldsymbol{X}}^{\rm{T}}} = {\boldsymbol{\varPhi}} _{{\rm{ACS}}}^{\rm{T}}{{\boldsymbol{G}}^{\rm{T}}} (22) 将
{{\boldsymbol{X}}^{\rm{T}}} 表示为列向量形式即{{\boldsymbol{X}}^{\rm{T}}} = \left[ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{x}}} }_1},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{x}}} }_2} \cdot \cdot \cdot ,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{x}}} }_M}} \right] ，将{{\boldsymbol{G}}^{\rm{T}}} 也表示为列向量形式即{{\boldsymbol{G}}^{\rm{T}}} = \left[ {{{\boldsymbol{g}}_{_1}},{{\boldsymbol{g}}_2}, \cdots ,{{\boldsymbol{g}}_M}} \right] ，那么欠定方程式(22)可以进一步写为{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{x}}} _m} = {\boldsymbol{\varPhi}} _{{\rm{ACS}}}^{\rm{T}}{{\boldsymbol{g}}_{m,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m = 1,2, \cdots ,M (23) 其中，
{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{x}}} _m} \in {\mathbb{C}^Q} ，{{\boldsymbol{g}}_m} \in {\mathbb{C}^N} ，M 为距离向采样点。对方位向压缩感知模型也使用本文提出的迭代近端投影的方法求解，求解得到稀疏向量{{\boldsymbol{g}}_m} ，进一步得到2维的SAR图像。4. 仿真结果与分析
为综合比较分析本文方法的性能，将正交匹配追踪(OMP)算法、平滑l0范数(Smoothed l0 norm, SL0)算法、贝叶斯压缩感知(Bayesian Compressive Sensing, BCS)算法与本文提出的迭代近端投影(Iterative Proximal Projection, IPP)算法作为对比；同时，为进一步定量分析成像结果，本文利用目标杂波比(Target to Clutter Ratio, TCR)[18]和图像熵(Image Entropy, IE)[18]来定量评价成像质量，用成像时间来评定算法的运算效率。同时，为验证算法在噪声情况下的性能，对回波加入高斯白噪声进行仿真实验。
4.1 不同采样率成像实验
为进一步验证算法的性能，对30个点目标仿真产生的数据在不同采样率和不同信噪比条件下进行仿真实验。主要仿真参数设置如表1所示。为方便分析，设置相同的距离采样率和方位采样率
\delta 。图3给出了目标散射点模型与不同采样率下各算法成像结果图，其中图3(a)为散射点模型，图3(b-e)表示采样率为原采样率1/2时4种算法成像结果。图3(f-i)表示采样率为原采样率1/4时4种算法成像结果。表 1 雷达仿真参数参数 数值 雷达信号载频 3 GHz 雷达信号带宽 150 MHz 采样频率 300 MHz 雷达距目标区域中心点 4200 m 由图3可以看出，在采样率为原采样率1/2时，几种算法都可以清晰地实现目标点SAR成像；当采样率为1/4时，OMP算法的成像效果变差，其他算法依然能够清晰成像。
为了进一步比较上述算法的成像质量，利用TCR和IE作为衡量指标。图4(a)、图4(b)分别给出了不同采样率条件下几种算法的TCR及IE对比曲线，从图4(a)可以看出，随着采样率的下降，SL0算法、BCS算法与本文算法的TCR相对保持稳定，而OMP算法在采样率较低时产生较大波动。同时，可以看出，本文算法的TCR一直大于其他算法，说明本文算法成像结果聚焦性能更好，虚假散射点更少。从图4(b)可以看出，本文算法的IE一直低于其他算法，进一步说明本文算法具有很好的成像性能。
为进一步验证算法的运算效率，表2给出了采样率同为原采样率的1/2时几种算法成像时间对比，从中进一步得出本文算法成像时间也相对较短。说明本文算法在保证成像质量的前提下能够实现快速成像。
表 2 采样率为原采样率1/2时各算法成像时间算法 时间(s) IPP 26.7381 OMP 18.7749 SL0 27.3091 BCS 178.2851 4.2 抗噪声性能实验
首先在不同信噪比条件下进行数据仿真实验，将距离向采样率和方位向采样率同时设置为原采样率的1/2，即
\delta = \dfrac{1}{2} ，并在回波信号处添加高斯白噪声使SNR分别为–10 dB和20 dB。成像结果如图5，其中图5(a)—图5(d)为SNR=20 dB时4种算法成像结果，图5(e)—图5(h)为SNR=–10 dB时4种算法成像结果。由图5可以看出，当信噪比为20 dB时，几种算法都可以清晰成像；当采样率为–10 dB时，OMP算法与BCS算法成像结果出现严重失真，SL0算法成像结果虽可以成像，但是出现较多虚假目标，只有本文算法受噪声影响较小，可以较为清晰地成像。为了进一步验证算法的鲁棒性，以TCR, IE作为衡量指标。图6(a)、图6(b)分别为不同信噪比条件下各算法的TCR与IE曲线，由图6(a)可以看出，随着信噪比的上升，各算法的TCR逐渐上升，但在较低信噪比时本文算法依然高于其他算法，说明本文算法有一定的抗噪声能力。同时，由图6(b)可以得出，本文算法的IE随着信噪比的上升逐渐下降且一直低于其他算法，进一步说明本文算法具有良好的鲁棒性。综合实验对比可知，本文算法相较于其他算法具有更好的欠采样成像能力。
5. 实测数据处理
为了充分验证本文算法对实际场景处理的有效性，本文将采用来自加拿大温哥华RADARSAT-1精细模式2(加拿大航天局版权所有)的实测数据进行实验。主要参数设置如表3所示。图7给出各算法成像结果，其中图7(a)为基于距离多普勒算法的温哥华地区英吉利海湾附近区域的实测场景图。本文将选取图7(a)中红色矩形区域中6个目标点(即6艘货船)进行实验，其原因是这6个目标点相较于海平面来说是强散射点，而又相较于英吉利海湾是稀疏的。图7(b)—图7(e)是4种算法在距离采样率为0.5，方位采样率为0.3时的成像结果。成像结果表明，当采样数据量减少后，本文算法仍能重建出目标，且相较于其他算法能够消除图像中的模糊，进一步验证了本文算法的有效性。
表 3 温哥华场景RADARSAT-1参数参数 数值 距离带宽 30.3 MHz 距离向采样频率 32.317 MHz 脉冲宽度 30.111 MHz 卫星轨道半径 7186029 m 雷达波长 0.05657 m 6. 结束语
针对RD等成像算法存在数据量大、采样率高及OMP、SL0和BCS等算法存在成像精度低及抗噪性能差等问题，本文提出一种迭代近端投影的2维欠采样SAR成像方法，首先对SAR回波信号进行分析，构建基于距离向与方位向的稀疏表示模型，在此基础上，利用近端函数优化模型来表示距离向与方位向稀疏模型，并采用SCAD函数获得近端算子来求解该模型。仿真和实际数据结果验证了该方法的有效性。结果表明，该文方法在低采样率以及低信噪比条件下成像结果优于OMP算法、SL0算法与BCS算法。
-
表 3 温哥华场景RADARSAT-1参数
参数 数值 距离带宽 30.3 MHz 距离向采样频率 32.317 MHz 脉冲宽度 30.111 MHz 卫星轨道半径 7186029 m 雷达波长 0.05657 m 
下载: 导出CSV
-
[1] ZHU Hongliang, LEUNG R, and HONG Minyi. Shadow compensation for synthetic aperture radar target classification by dual parallel generative adversarial network[J]. IEEE Sensors Letters, 2020, 4(8): 7002904. doi: 10.1109/LSENS.2020.3009179 [2] XIAO Peng, LIU Bo, and GUO Wei. ConGaLSAR: A constellation of geostationary and low earth orbit synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2085–2089. doi: 10.1109/LGRS.2019.2962574 [3] 杨磊, 张苏, 黄博, 等. 多任务协同优化学习高分辨SAR稀疏自聚焦成像算法[J]. 电子与信息学报, 2021, 43(9): 2711–2719. doi: 10.11999/JEIT200300YANG Lei, ZHANG Su, HUANG Bo, et al. Multi-task learning of sparse autofocusing for high-resolution SAR imagery[J]. Journal of Electronics &Information Technology, 2021, 43(9): 2711–2719. doi: 10.11999/JEIT200300 [4] 田鹤, 于海锋, 朱宇, 等. 基于频域稀疏压缩感知的星载SAR稀疏重航过3维成像[J]. 电子与信息学报, 2020, 42(8): 2021–2028. doi: 10.11999/JEJT190638TIAN He, YU Haifeng, ZHU Yu, et al. Sparse flight 3-D imaging of spaceborne SAR based on frequency domain sparse compressed sensing[J]. Journal of Electronics &Information Technology, 2020, 42(8): 2021–2028. doi: 10.11999/JEJT190638 [5] BU Hongxia, BAI Xia, and TAO Ran. Compressed sensing SAR imaging based on sparse representation in fractional Fourier domain[J]. Science China Information Sciences, 2012, 55(8): 1789–1800. doi: 10.1007/s11432-012-4607-6 [6] PATEL V M, EASLEY G R, HEALY D M, et al. Compressed synthetic aperture radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 244–254. doi: 10.1109/JSTSP.2009.2039181 [7] DONG Xiao and ZHANG Yunhua. A novel compressive sensing algorithm for SAR imaging[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(2): 708–720. doi: 10.1109/JSTARS.2013.2291578 [8] LIU Zhixue, LI Gang, ZHANG Hao, et al. SAR imaging of dominant scatterers using cascading StOMP[C]. Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 1676–1679. [9] BU Hongxia, TAO Ran, BAI Xia, et al. A novel SAR imaging algorithm based on compressed sensing[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 1003–1007. doi: 10.1109/LGRS.2014.2372319 [10] 徐建平, 皮亦鸣, 曹宗杰. 基于贝叶斯压缩感知的合成孔径雷达高分辨成像[J]. 电子与信息学报, 2011, 33(12): 2863–2868. doi: 10.3724/SP.J.1146.2010.01377XU Jianping, PI Yiming, and CAO Zongjie. SAR imaging based on Bayesian compressive sensing[J]. Journal of Electronics &Information Technology, 2011, 33(12): 2863–2868. doi: 10.3724/SP.J.1146.2010.01377 [11] 梁美美. 基于压缩感知的SAR成像算法研究[D]. [硕士论文], 哈尔滨工程大学, 2014.LIANG Meimei. Research of SAR imaging arithmetic based on compressed sensing[D]. [Master dissertation], Harbin Engineering University, 2014. [12] LI Shiyong, ZHAO Guoqiang, LI Houmin, et al. Near-field radar imaging via compressive sensing[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(2): 828–833. doi: 10.1109/TAP.2014.2381262 [13] GHAYEM F, SADEGHI M, BABAIE-ZADEH M, et al. Sparse signal recovery using iterative proximal projection[J]. IEEE Transactions on Signal Processing, 2018, 66(4): 879–894. doi: 10.1109/TSP.2017.2778695 [14] CHEN Jinli, ZHENG Yao, ZHANG Tingxiao, et al. Iterative reweighted proximal projection based DOA estimation algorithm for monostatic MIMO radar[J]. Signal Processing, 2020, 172: 107537. doi: 10.1016/j.sigpro.2020.107537 [15] FAN Jianqing and LI Runze. Variable selection via Nonconcave penalized likelihood and its oracle properties[J]. Journal of the American Statistical Association, 2001, 96(456): 1348–1360. doi: 10.1198/016214501753382273 [16] 卜红霞, 白霞, 赵娟, 等. 基于压缩感知的矩阵型联合SAR成像与自聚焦算法[J]. 电子学报, 2017, 45(4): 874–881. doi: 10.3969/j.issn.0372-2112.2017.04.016BU Hongxia, BAI Xia, ZHAO Juan, et al. Joint matrix form SAR imaging and autofocus based on compressed sensing[J]. Acta Electronica Sinica, 2017, 45(4): 874–881. doi: 10.3969/j.issn.0372-2112.2017.04.016 [17] TSENG P. Convergence of a block coordinate descent method for nondifferentiable minimization[J]. Journal of Optimization Theory and Applications, 2001, 109(3): 475–494. doi: 10.1023/A:1017501703105 [18] 徐楚, 朱栋强, 汪玲, 等. 基于零空间 {l_1} 范数最小化的ISAR成像方法[J]. 系统工程与电子技术, 2020, 42(2): 315–321. doi: 10.3969/j.issn.1001-506X.2020.02.09XU Chu, ZHU Dongqiang, WANG Ling, et al. ISAR imaging using null space l1 norm minimization[J]. Systems Engineering and Electronics, 2020, 42(2): 315–321. doi: 10.3969/j.issn.1001-506X.2020.02.09 期刊类型引用(2)
1. 高志奇，李贺贺，黄平平，谭维贤，徐伟. 基于复合正则化的稀疏SAR成像方法研究. 信号处理. 2024(10): 1895-1909 . 
百度学术2. 贾金伟，刘利民，韩壮志，解辉. 基于压缩感知的抗SDIF分选射频隐身信号设计及回波信号处理. 航空学报. 2023(13): 220-243 . 百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 558
- HTML全文浏览量: 205
- PDF下载量: 86
- 被引次数: 3
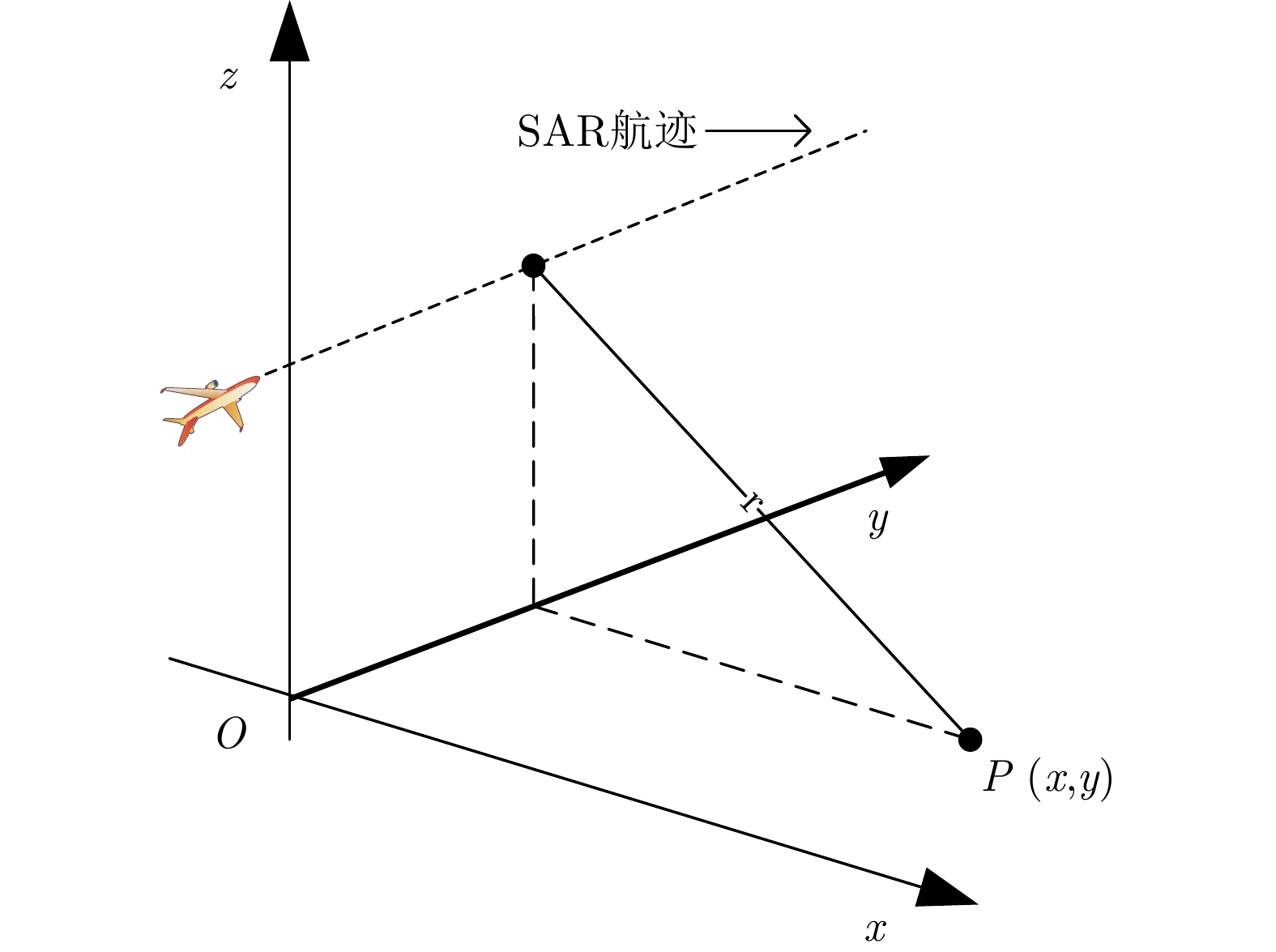
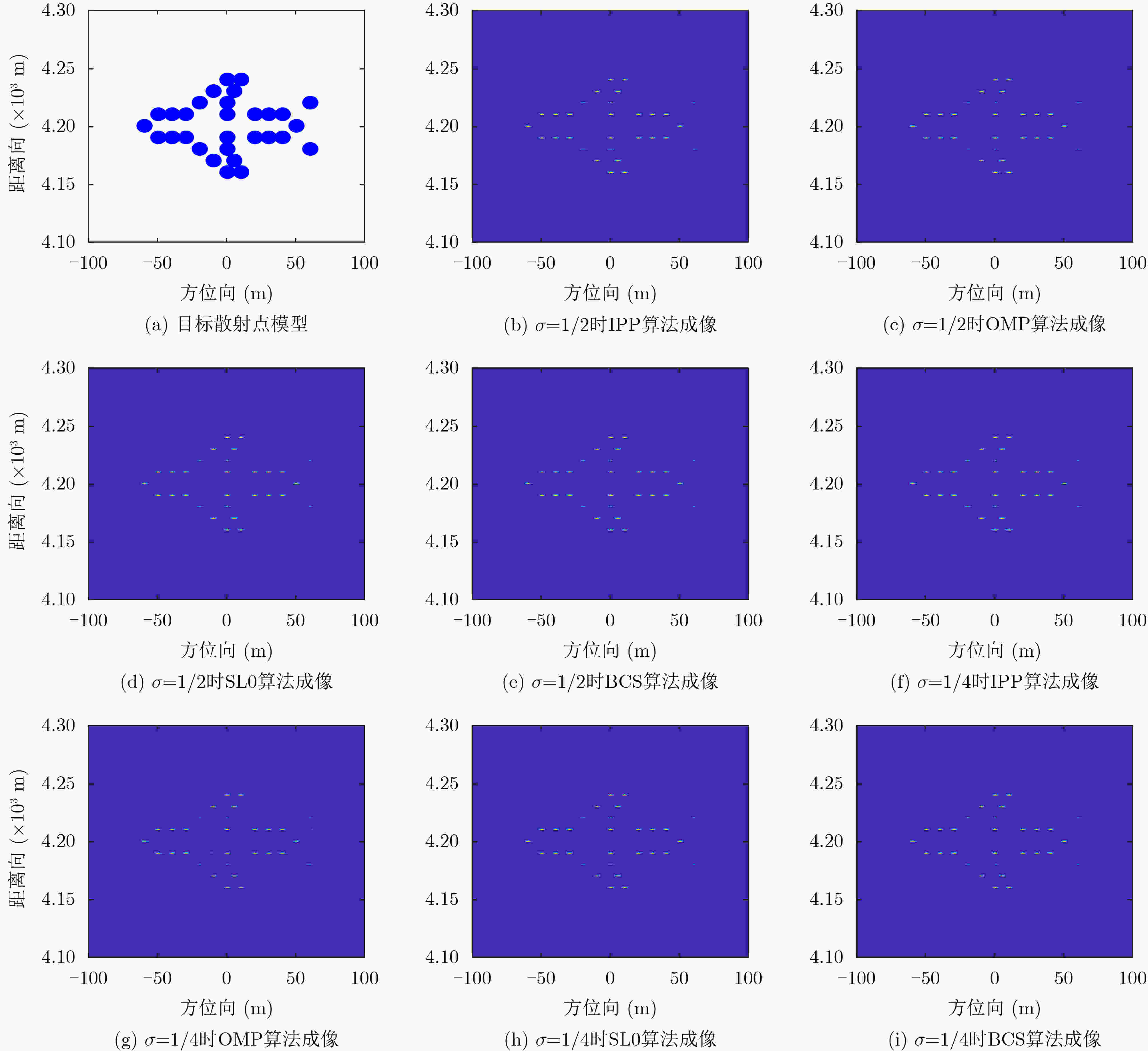
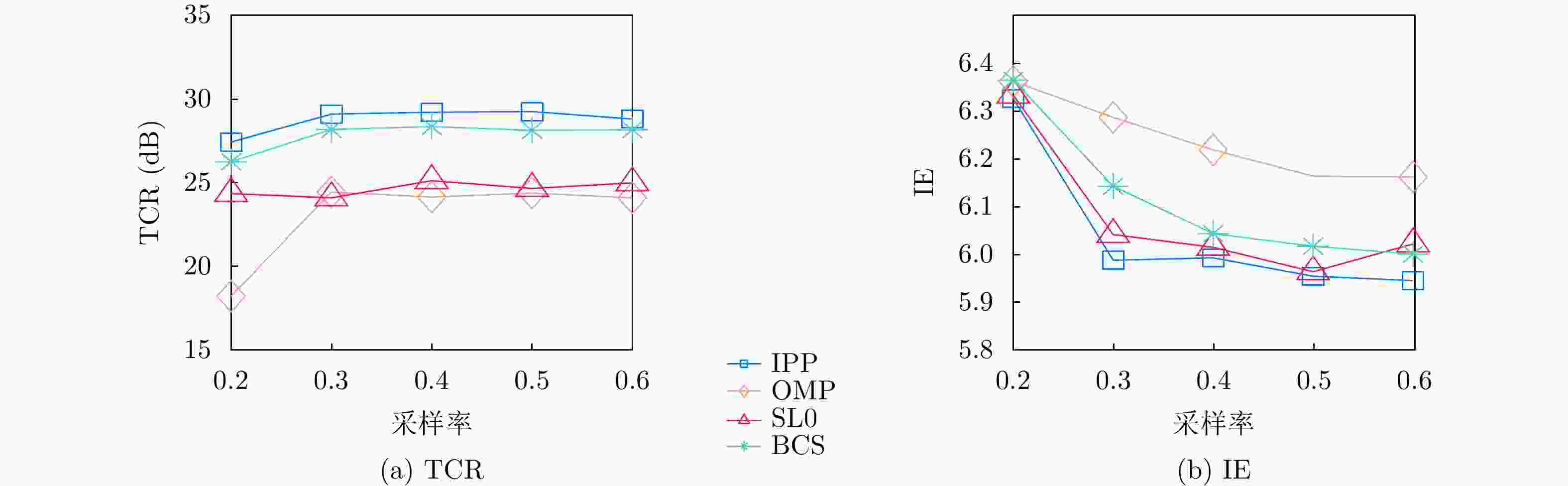
下载:
