一种基于欧氏距离的种群规模动态控制方法

季伟东; 倪婉璐

doi:10.11999/JEIT210322

一种基于欧氏距离的种群规模动态控制方法

doi: 10.11999/JEIT210322

季伟东^,,
倪婉璐

哈尔滨师范大学计算机科学与信息工程学院哈尔滨 150025

基金项目: 国家自然科学基金(31971015)，哈尔滨市科技局科技创新人才研究专项项目(2017RAQXJ050)，哈尔滨师范大学计算机科学与信息工程学院科研项目(JKYKYY202001)，2021年度黑龙江省自然科学基金(LH2021F037)

详细信息

作者简介:
季伟东：男，1978年生，博士，教授，研究方向为大数据、群体智能

倪婉璐：女，1996年生，硕士生，研究方向为群体智能

通讯作者:
季伟东　kingjwd@126.com

中图分类号: TP301
计量
- 文章访问数: 639
- HTML全文浏览量: 686
- PDF下载量: 91
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-19
- 修回日期: 2021-11-18
- 录用日期: 2021-11-18
- 网络出版日期: 2021-12-23
- 刊出日期: 2022-06-21

A Dynamic Control Method of Population Size Based on Euclidean Distance

JI Weidong^,,
NI Wanlu

School of Computer Science and Information Engineering, Harbin Normal University, Harbin 150025, China

Funds: The National Natural Science Foundation of China (31971015), Harbin Science and Technology Bureau’s Special Subsidy for Scientific and Technological Innovation Talents Research (2017RAQXJ050), The Research Project of School of Computer Science and Information Engineering,Harbin Normal University (JKYKYY202001), The Natural Science Foundation of Heilongjiang Province in 2021 (LH2021F037)

摘要

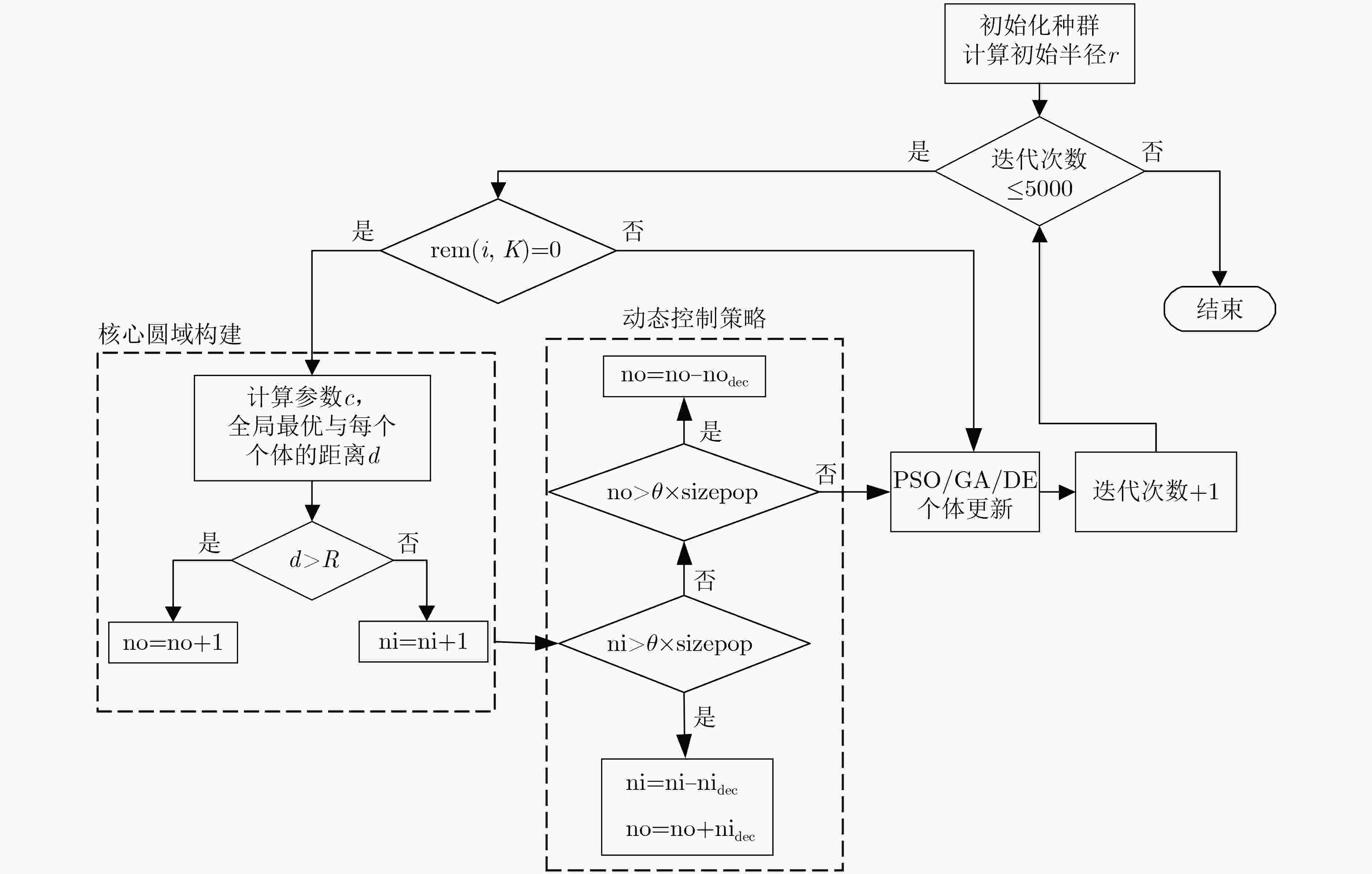
摘要: 种群规模是决定算法性能最重要的参数，其大小会引发算法过早收敛或效率低下等问题。该文提出一种基于欧氏距离的种群规模动态控制方法(EDPS)，通过引入欧氏距离建立核心圆域，利用核心圆域反馈的信息动态控制种群规模，提出基于核心圆域的增加/删除个体数目的方法。将该方法运用到粒子群算法、遗传算法和差分进化算法中，对收敛性进行分析，在测试函数上对其性能进行测试，实验结果表明了所提新策略的有效性。
- 欧氏距离 /
- 核心圆域 /
- 动态控制 /
- 种群规模 /
- 自然计算
Abstract: The population size is the most significant parameter to determine the performance of the algorithm, and its size may cause problems such as premature convergence or low efficiency of the algorithm. A dynamic control method of Population Size besed on Euclidean Distance (EDPS) is proposed. The core circle is established by adopting the Euclidean distance, and the feedback information of the core circle is used to control dynamically the population size, and the method of increasing or deleting the number of individuals based on the core circle is proposed. The strategy is applied to particle swarm optimization algorithm, genetic algorithm and differential evolution algorithm, whose performance is verified in the test functions. The experimental results show the proposed new strategy is effective.
- Euclidean distance /
- Core circle /
- Dynamic control /
- Population size /
- Natural computing

HTML全文

图 1 动态控制流程图

下载: 全尺寸图片幻灯片

图 2 算法流程图

下载: 全尺寸图片幻灯片

图 3 增删的不同个体数的收敛图

下载: 全尺寸图片幻灯片

图 4 收敛曲线

下载: 全尺寸图片幻灯片

图 5 收敛曲线

下载: 全尺寸图片幻灯片

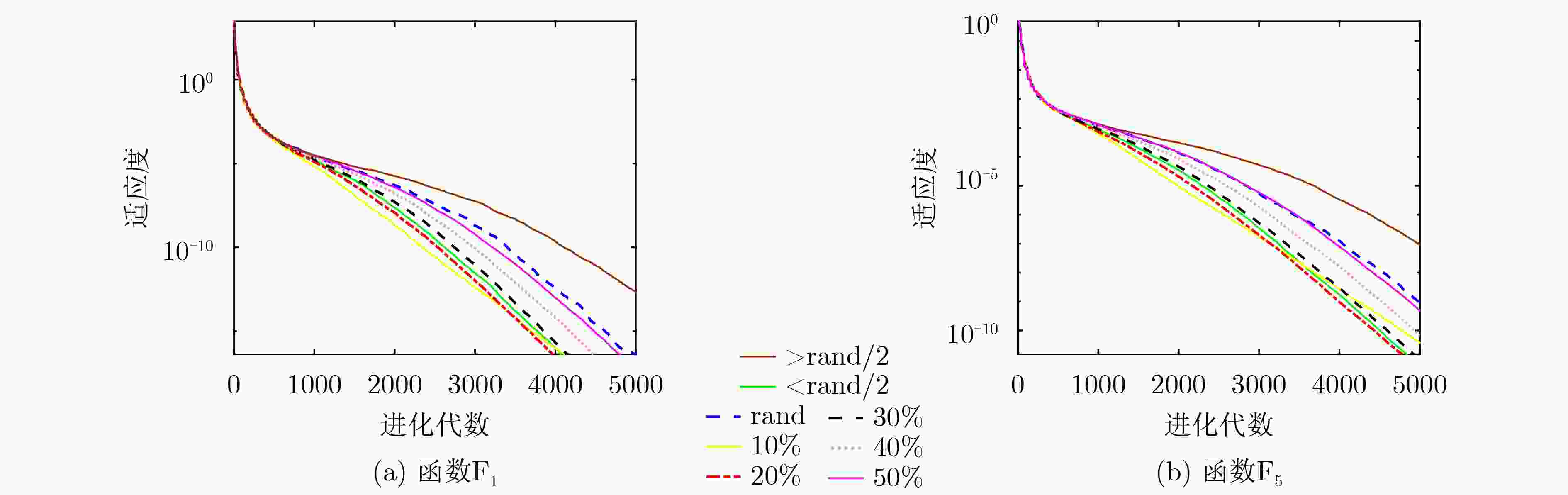
表 1 函数F₁和F₅基于激活阈值K和判定阈值θ的平均结果

		F₁	F₅
激活阈值K	K=0	2.4785×10^–9	2.2471×10^–04
	K=10	2.7143×10^–19	2.3246×10^–09
	K=20	5.4301×10^–23	3.2744×10^–11
	K=30	1.1969×10^–24	5.4805×10^–12
	K=40	1.1569×10^–24	3.7871×10^–12
	K=50	1.7930×10^–24	5.0300×10^–12
判定阈值θ	θ=1/2	2.9332×10^–24	6.7745×10^–12
	θ=2/3	2.0541×10²⁴	4.8624×10^–12
	θ=3/4	3.5091×10^–24	3.2218×10^–12
	θ=4/5	3.9844×10^–25	2.5269×10^–12
	θ=5/6	2.1254×10^–24	6.2672×10^–12

下载: 导出CSV

表 2 适应度值的平均值与标准差

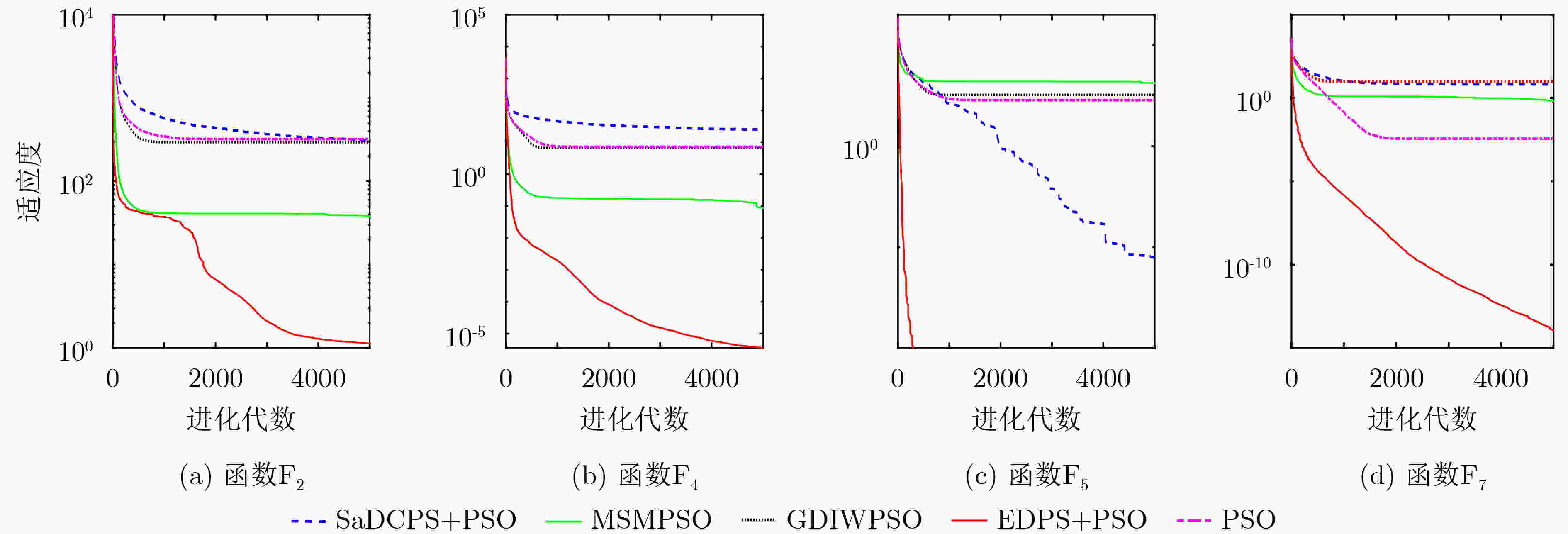
测试函数		PSO	SaDCPS+PSO	MSMPSO	GDIWPSO	EDPS+PSO
F₁	Mean Std	0.0048(5) 0.0036	5.2678E-05(2) 1.9733E-04	0.0035(4) 0.0048	5.4229E-04(3) 6.9283E-04	4.2030E-22(1) 5.4355E-22
F₂	Mean Std	321.6227(5) 757.5841	305.9853(4) 612.6810	37.8965(2) 20.8848	295.3553(3) 646.0457	1.1286(1) 1.2517
F₃	Mean Std	11.4856(3) 57.4760	35.6888(5) 96.4784	1.6279(2) 1.3055	15.3413(4) 59.2914	0.6667(1) 5.3114E-13
F₄	Mean Std	7.1478(4) 18.5511	24.8610(5) 39.5939	0.0869(2) 0.1725	6.5236(3) 21.1265	3.5356E-06(1) 1.6043E-06
F₅	Mean Std	2.8480(3) 0.6077	0.0794(2) 0.3244	4.2122(5) 1.8981	3.2137(4) 0.4853	4.0041E-12(1) 3.1655E-12
F₆	Mean Std	0.3953(2) 0.3879	4.7684(5) 8.2253	0.6478(3) 0.4967	0.7580(4) 0.4689	4.8769E-23(1) 6.2365E-23
F₇	Mean Std	0.0037(2) 0.0041	6.6792(4) 35.8988	0.6468(3) 0.6773	10.1297(5) 29.9757	1.1530E-14(1) 2.8465E-14
F₈	Mean Std	0.0364(2) 0.0198	0.0824(3) 0.2486	0.6663(5) 0.2804	0.2826(4) 0.1051	0.0133(1) 0.0205
F₉	Mean Std	41.3446(5) 12.1342	17.7337(2) 13.9827	24.1869(3) 10.0910	45.9872(4) 14.3957	1.3145E-14(1) 5.7943E-15
F₁₀	Mean Std	2.0873(4) 4.0499	3.0617(5) 4.6183	1.4784(3) 1.1296	1.4486(2) 4.4262	6.0354E-07(1) 1.0596E-06
F₁₁	Mean Std	0.0069(2) 0.0083	0.4674(4) 0.1805	1.1304(5) 1.2018	0.1760(3) 0.1348	1.8818E-21(1) 3.2949E-21
Num		0	0	0	0	11
Ave.R		3.36	3.18	3.36	3.54	1
T.R		3	2	4	5	1

下载: 导出CSV

表 3 适应度值的平均值与标准差

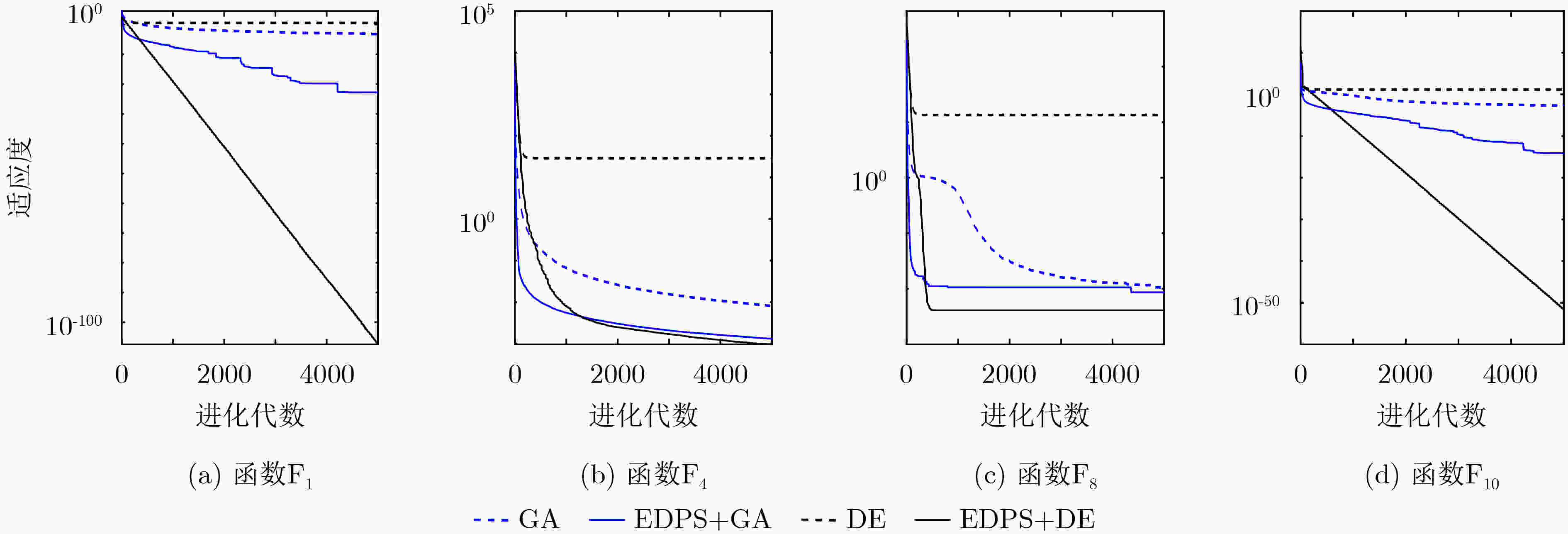
测试函数		GA	EDPS+GA	DE	EDPS+DE
F₁	Mean Std	6.1788×10^–4 4.3273×10^–4	1.6779×10^–23 9.0360×10^–23	3.6639 1.3679	3.8710×10^–108 1.6719×10^–107
F₂	Mean Std	27.2667 0.7982	37.3328 24.9148	3.9463×10³ 3.7519×10³	57.1605 34.2014
F₃	Mean Std	0.6668 9.7515×10^–5	0.6667 3.0891×10^–6	839.0467 813.5188	0.7655 0.4595
F₄	Mean Std	0.0081 0.0020	0.0013 2.8946×10^–04	28.8509 18.4569	9.6287×10^–4 4.9931×10^–4
F₅	Mean Std	0.0059 0.0021	2.2649×10^–13 3.2758×10^–13	7.6543 1.0717	1.5099×10^–14 3.8918×10^–15
F₆	Mean Std	2.5529×10^–5 1.4647×10^–5	1.2247×10^–06 1.5500×10^–06	2.5036 1.3115	0.0322 0.0509
F₇	Mean Std	1.1032×10^–04 8.6325×10^–05	1.5921×10^–26 8.5642×10^–26	159.1248 69.8944	3.1682×10^–106 9.8938×10^–106
F₈	Mean Std	0.0106 0.0112	0.0087 0.0162	13.4697 5.7995	0.0041 0.0054
F₉	Mean Std	7.4007×10^–4 4.0655×10^–4	0 0	140.2000 19.1678	0 0
F₁₀	Mean Std	0.0020 5.5404×10^–4	7.9361×10^–15 4.0250×10^–14	14.9866 3.2050	1.7483×10^–52 3.7124×10^–52
F₁₁	Mean Std	5.9413×10^–4 4.0894×10^–4	2.5991×10^–6 1.6006×10^–6	1.3808×10³ 526.4687	0.1605 0.1092

下载: 导出CSV

表 4 适应度值的平均结果对比

测试函数	EDPS+GA	GAVaPS	APAGA	PL-GA	GPS-GA	EDPS+DE	dynNP-DE	SAMDE
F₁	8.09×10^–310	5.02×10^–5	5.01×10^–5	5.02×10^–5	5.04×10^–5	0	5.02×10^–5	5.02×10^–5
F₈	0.0197	4.94×10^–2	5.14×10^–2	5.74×10^–2	4.91×10^–2	0.0209	5.08×10^–2	3.87×10^–2
F₉	0	–1.02×10¹	–1.02	–1.03×	–1.02	0	–1.03	–1.03
F₁₁	1.67×10^–8	0.11×10	0.11	0	0	0.3508	0	0.00

下载: 导出CSV

表 5 适应度值的运行平均结果

函数	PSO	EDPS+PSO	GA	EDPS+GA	DE	EDPS+DE
F₁	1.84×10³	5.46×10^–13	6.38×10^–3	2.74×10^-2	5.69×10³	6.96×10²
F₂	9.82×10⁶	1.12×10⁵	6.24×10⁶	6.66×10⁶	1.00×10⁷	6.84×10⁶
F₅	9.39×10²	1.83×10^–4	1.91×10^–2	6.03×10^-2	1.50×10²	5.00×10¹
F₆	1.54×10²	1.08×10¹	7.57×10¹	6.19×10¹	2.79×10³	1.16×10²
F₁₀	3.99×10²	1.08×10¹	1.46	1.61	5.08×10²	1.45×10²
F₁₁	1.41×10²	5.02×10¹	1.82×10^–1	4.87×10²	1.67×10²	1.24×10¹
F₁₄	2.83×10³	1.38×10³	1.25×10¹	4.16×10^–1	6.51×10³	7.62×10²
F₁₆	1.32	9.32×10^–1	1.27	1.74	2.53	1.82
F₁₇	1.38×10²	3.47×10¹	4.24×10¹	3.06×10¹	2.45×10²	3.18×10¹
F₁₉	4.91×10²	2.95	1.25	8.88×10^–1	2.23×10²	4.72
F₂₀	3.86×10²	3.35×10²	5.14×10²	3.24×10+02	9.91×10²	6.08×10²
F₂₁	3.64×10³	1.72×10³	1.29×10²	1.04×10+02	6.74×10³	7.10×10²
F₂₃	2.87×10²	2.80×10²	2.94×10²	3.16×10²	2.41×10²	2.33×10²
F₂₄	2.98×10²	2.95×10²	3.50×10²	3.43×10+02	2.65×10²	2.63×10²
F₂₅	3.33×10²	2.05×10²	2.02×10²	2.25×10²	2.002×10²	2.001×10²

下载: 导出CSV

参考文献(43)

[1]	王蓉芳, 焦李成, 刘芳, 等. 自适应动态控制种群规模的自然计算方法[J]. 软件学报, 2012, 23(7): 1760–1772. doi: 10.3724/SP.J.1001.2012.04151 WANG Rongfang, JIAO Licheng, LIU Fang, et al. Nature computation with self-adaptive dynamic control strategy of population Size[J]. Journal of Software, 2012, 23(7): 1760–1772. doi: 10.3724/SP.J.1001.2012.04151
[2]	康琦, 安静, 汪镭, 等. 自然计算的研究综述[J]. 电子学报, 2012, 40(3): 548–558. doi: 10.3969/j.issn.0372-2112.2012.03.023 KANG Qi, AN Jing, WANG Lei, et al. Nature-inspired computation: A survey[J]. Acta Electronica Sinica, 2012, 40(3): 548–558. doi: 10.3969/j.issn.0372-2112.2012.03.023
[3]	SUN Shiyuan and LI Jianwei. A two-swarm cooperative particle swarms optimization[J]. Swarm and Evolutionary Computation, 2014, 15: 1–18. doi: 10.1016/j.swevo.2013.10.003
[4]	夏学文, 刘经南, 高柯夫, 等. 具备反向学习和局部学习能力的粒子群算法[J]. 计算机学报, 2015, 38(7): 1397–1407. doi: 10.11897/SP.J.1016.2015.01397 XIA Xuewen, LIU Jingnan, GAO Kefu, et al. Particle swarm optimization algorithm with reverse-learning and local-learning behavior[J]. Chinese Journal of Computers, 2015, 38(7): 1397–1407. doi: 10.11897/SP.J.1016.2015.01397
[5]	邓先礼, 魏波, 曾辉, 等. 基于多种群的自适应迁移PSO算法[J]. 电子学报, 2018, 46(8): 1858–1865. doi: 10.3969/j.issn.0372-2112.2018.08.009 DENG Xianli, WEI Bo, ZENG Hui, et al. A multi-population based self-adaptive migration PSO[J]. Acta Electronica Sinica, 2018, 46(8): 1858–1865. doi: 10.3969/j.issn.0372-2112.2018.08.009
[6]	张迅, 王平, 邢建春, 等. 基于高斯函数递减惯性权重的粒子群优化算法[J]. 计算机应用研究, 2012, 29(10): 3710–3712,3724. doi: 10.3969/j.issn.1001-3695.2012.10.027 ZHANG Xun, WANG Ping, XING Jianchun, et al. Particle swarm optimization algorithms with decreasing inertia weight based on Gaussian function[J]. Application Research of Computers, 2012, 29(10): 3710–3712,3724. doi: 10.3969/j.issn.1001-3695.2012.10.027
[7]	XU Guiping, CUI Quanlong, SHI Xiaohu, et al. Particle swarm optimization based on dimensional learning strategy[J]. Swarm and Evolutionary Computation, 2019, 45: 33–51. doi: 10.1016/j.swevo.2018.12.009
[8]	WEISE T, WU Yuezhong, CHIONG R, et al. Global versus local search: The impact of population sizes on evolutionary algorithm performance[J]. Journal of Global Optimization, 2016, 66(3): 511–534. doi: 10.1007/s10898-016-0417-5
[9]	徐晓华, 陈崚, 陈宏建. 可变种群规模的遗传算法[J]. 系统仿真学报, 2006, 18(4): 870–872,876. doi: 10.3969/j.issn.1004-731X.2006.04.015 XU Xiaohua, CHEN Ling, and CHEN Hongjian. Genetic algorithm with variable population size[J]. Journal of System Simulation, 2006, 18(4): 870–872,876. doi: 10.3969/j.issn.1004-731X.2006.04.015
[10]	AFFENZELLER M, WAGNER S, and WINKLER S. Self-adaptive population size adjustment for genetic algorithms[C]. The 11th International Conference on Computer Aided Systems Theory, Las Palmas de Gran Canaria, Spain, 2007: 820–828.
[11]	WANG Hui, RAHNAMAYAN S, and WU Zhijian. Adaptive Differential Evolution with variable population size for solving high-dimensional problems[C]. The IEEE Congress of Evolutionary Computation (CEC), New Orleans, USA, 2011: 2626–2632.
[12]	GUAN Yuyang, YANG Ling, and SHENG Weiguo. Population control in evolutionary algorithms: Review and comparison[C]. The 12th International Conference on Bio-inspired Computing: Theories and Applications, Harbin, China, 2017: 161–174.
[13]	PATEL S P and UPADHYAY S H. Euclidean distance based feature ranking and subset selection for bearing fault diagnosis[J]. Expert Systems with Applications, 2020, 154: 113400. doi: 10.1016/j.eswa.2020.113400
[14]	BOULEY S, VANWYNSBERGHE C, LE MAGUERESSE T, et al. Microphone array positioning technique with Euclidean distance geometry[J]. Applied Acoustics, 2020, 167: 107377. doi: 10.1016/j.apacoust.2020.107377
[15]	ALGULIYEV R M, ALIGULIYEV R M, and SUKHOSTAT L V. Weighted consensus clustering and its application to Big data[J]. Expert Systems with Applications, 2020, 150: 113294. doi: 10.1016/j.eswa.2020.113294
[16]	史哲文, 白雪石, 郭禾. 基于改进小生境粒子群算法的多模函数优化[J]. 计算机应用研究, 2012, 29(2): 465–468. doi: 10.3969/j.issn.1001-3695.2012.02.016 SHI Zhewen, BAI Xueshi, and GUO He. Multimodal function optimization based on modified niching particle swarm optimization[J]. Application Research of Computers, 2012, 29(2): 465–468. doi: 10.3969/j.issn.1001-3695.2012.02.016
[17]	王通, 刘文芳, 刘春芳. 基于欧氏距离的黑洞寻优算法[J]. 沈阳工业大学学报, 2016, 38(2): 201–205. doi: 10.7688/j.issn.1000-1646.2016.02.15 WANG Tong, LIU Wenfang, and LIU Chunfang. Optimization algorithm of black-hole based on Euclidean distance[J]. Journal of Shenyang University of Technology, 2016, 38(2): 201–205. doi: 10.7688/j.issn.1000-1646.2016.02.15
[18]	佘合一, 吴锡生. 基于欧氏距离与多种搜索策略的人工蜂群算法[J]. 传感器与微系统, 2018, 37(9): 132–135. doi: 10.13873/J.1000-9787(2018)09-0132-04 SHE Heyi and WU Xisheng. ABC algorithm based on Euclidean distance and multiple search strategies[J]. Transducer and Microsystem Technologies, 2018, 37(9): 132–135. doi: 10.13873/J.1000-9787(2018)09-0132-04
[19]	吴辰文, 马宁, 蒋雨璠. 基于Jeffrey散度相似性度量的加权FCM聚类算法[J]. 激光与光电子学进展, 2021, 58(8): 0810006. doi: 10.3788/LOP202158.0810006 WU Chenwen, MA Ning, and JIANG Yufan. Weighted FCM clustering algorithm based on Jeffrey divergence similarity measure[J]. Laser &Optoelectronics Progress, 2021, 58(8): 0810006. doi: 10.3788/LOP202158.0810006
[20]	束俊, 孟德宇, 徐宗本. 元自步学习[J]. 中国科学:信息科学, 2020, 50(6): 781–793. doi: 10.1360/SSI-2020-0005 SHU Jun, MENG Deyu, and XU Zongben. Meta self-paced learning[J]. Scientia Sinica Informationis, 2020, 50(6): 781–793. doi: 10.1360/SSI-2020-0005
[21]	SRISTI P, LU W S, and ANTONIOU A. A new variable-step-size LMS algorithm and its application in subband adaptive filtering for echo cancellation[C]. The IEEE International Symposium on Circuits and Systems, Sydney, Australia, 2001: 721–724.
[22]	吕春英, 敖伟, 张洪顺. 一种新的变步长LMS算法[J]. 通信技术, 2011, 44(3): 11–14. doi: 10.3969/j.issn.1002-0802.2011.03.005 LV Chunying, AO Wei, and ZHANG Hongshun. A new variable step-size LMS algorithm[J]. Communications Technology, 2011, 44(3): 11–14. doi: 10.3969/j.issn.1002-0802.2011.03.005
[23]	张喜涛, 张安清. 基于Sigmoid函数的变步长LMS自适应滤波算法性能分析[J]. 舰船电子对抗, 2013, 36(6): 52–55,82. doi: 10.3969/j.issn.1673-9167.2013.06.013 ZHANG Xitao and ZHANG Anqing. Performance analysis of LMS adaptive filtering algorithm with variable step based on Sigmoid function[J]. Shipboard Electronic Countermeasure, 2013, 36(6): 52–55,82. doi: 10.3969/j.issn.1673-9167.2013.06.013
[24]	付学志, 刘忠, 李朝旭. Sigmoid函数变步长LMS自适应算法的抗干扰性能改进[J]. 北京邮电大学学报, 2011, 34(6): 112–115,120. doi: 10.3969/j.issn.1007-5321.2011.06.026 FU Xuezhi, LIU Zhong, and LI Chaoxu. Anti-interference performance improvement for Sigmoid function variable step-size LMS adaptive algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(6): 112–115,120. doi: 10.3969/j.issn.1007-5321.2011.06.026
[25]	徐洋, 徐松涛, 马健, 等. 基于Sigmoid二次型隶属度函数的改进LMS算法[J]. 中南大学学报:自然科学版, 2014, 45(10): 3470–3476. XU Yang, XU Songtao, MA Jian, et al. Improved LMS algorithm based on Sigmoid quadratic membership function[J]. Journal of Central South University:Science and Technology, 2014, 45(10): 3470–3476.
[26]	王平波, 马凯, 武彩. 基于正态分布曲线的分段式变步长LMS算法[J]. 国防科技大学学报, 2020, 42(5): 16–22. doi: 10.11887/j.cn.202005003 WANG Pingbo, MA Kai, and WU Cai. Segmented variable-step-size LMS algorithm based on normal distribution curve[J]. Journal of National University of Defense Technology, 2020, 42(5): 16–22. doi: 10.11887/j.cn.202005003
[27]	TIZHOOSH H R. Opposition-based learning: A new scheme for machine intelligence[C]. International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, Vienna, Austria, 2005: 695–701.
[28]	WANG Hui, WU Zhijian, RAHNAMAYAN S, et al. Enhancing particle swarm optimization using generalized opposition-based learning[J]. Information Sciences, 2011, 181(20): 4699–4714. doi: 10.1016/j.ins.2011.03.016
[29]	罗强, 季伟东, 徐浩天, 等. 一种最优粒子逐维变异的粒子群优化算法[J]. 小型微型计算机系统, 2020, 41(2): 259–263. doi: 10.3969/j.issn.1000-1220.2020.02.006 LUO Qiang, JI Weidong, XU Haotian, et al. Particle swarm optimization with global best particle dimension-by-dimension mutation[J]. Journal of Chinese Computer Systems, 2020, 41(2): 259–263. doi: 10.3969/j.issn.1000-1220.2020.02.006
[30]	RAHNAMAYAN S, JESUTHASAN J, BOURENNANI F, et al. Computing opposition by involving entire population[C]. IEEE Congress on Evolutionary Computation, Beijing, China, 2014: 1800–1807.
[31]	XU Gang and YU Guosong. Reprint of: On convergence analysis of particle swarm optimization algorithm[J]. Journal of Computational and Applied Mathematics, 2018, 340: 709–717. doi: 10.1016/j.cam.2018.04.036
[32]	骆剑平, 李霞, 陈泯融. 混合蛙跳算法的Markov模型及其收敛性分析[J]. 电子学报, 2010, 38(12): 2875–2880. LUO Jianping, LI Xia, and CHEN Minrong. The Markov model of shuffled frog leaping algorithm and its convergence analysis[J]. Acta Electronica Sinica, 2010, 38(12): 2875–2880.
[33]	潘峰, 周倩, 李位星, 等. 标准粒子群优化算法的马尔科夫链分析[J]. 自动化学报, 2013, 39(4): 381–389. doi: 10.3724/SP.J.1004.2013.00381 PAN Feng, ZHOU Qian, LI Weixing, et al. Analysis of standard particle swarm optimization algorithm based on Markov chain[J]. Acta Automatica Sinica, 2013, 39(4): 381–389. doi: 10.3724/SP.J.1004.2013.00381
[34]	SOLIS F J and WETS R J B. Minimization by random search techniques[J]. Mathematics of Operations Research, 1981, 6(1): 19–30. doi: 10.1287/moor.6.1.19
[35]	季伟东, 孙小晴, 林平, 等. 基于非线性降维的自然计算方法[J]. 电子与信息学报, 2020, 42(8): 1982–1989. doi: 10.11999/JEIT190623 JI Weidong, SUN Xiaoqing, LIN Ping, et al. Natural computing method based on nonlinear dimension reduction[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1982–1989. doi: 10.11999/JEIT190623
[36]	周新宇, 吴志健, 王晖, 等. 一种精英反向学习的粒子群优化算法[J]. 电子学报, 2013, 41(8): 1647–1652. doi: 10.3969/j.issn.0372-2112.2013.08.031 ZHOU Xinyu, WU Zhijian, WANG Hui, et al. Elite opposition-based particle swarm optimization[J]. Acta Electronica Sinica, 2013, 41(8): 1647–1652. doi: 10.3969/j.issn.0372-2112.2013.08.031
[37]	ARABAS J, MICHALEWICZ Z, and MULAWKA J. GAVaPS-a genetic algorithm with varying population size[C]. The First IEEE Conference on Evolutionary Computation. IEEE World Congress on Computational Intelligence, Orlando, USA, 1994: 73–78.
[38]	BÄCK T, EIBEN A E, and VAN DER VAART N A L. An emperical study on GAs "without parameters"[C]. The 6th International Conference on Parallel Problem Solving from Nature PPSN VI, Paris, France, 2000: 315–324.
[39]	HOLDENER E A. The art of parameterless evolutionary algorithms[D]. [Ph. D. dissertation], Missouri University of Science and Technology, 2008.
[40]	SMORODKINA E and TAURITZ D. Greedy population sizing for evolutionary algorithms[C]. IEEE Congress on Evolutionary Computation (CEC), Singapore, 2007: 2181–2187.
[41]	BREST J and MAUČEC M S. Population size reduction for the differential evolution algorithm[J]. Applied Intelligence, 2008, 29(3): 228–247. doi: 10.1007/s10489-007-0091-x
[42]	WANG Xu, ZHAO Shuguang, JIN Yanling, et al. Differential evolution algorithm based on self-adaptive adjustment mechanism[C]. The 25th Chinese Control and Decision Conference, Guiyang, China, 2013: 577–581.
[43]	LIANG J J, QU B Y, SUGANTHAN P N, et al. Problem definitions and evaluation criteria for the CEC 2013 special session on real-parameter optimization[R]. Technical Report 201212, 2013.