Differential Privacy Algorithm under Deep Neural Networks
-
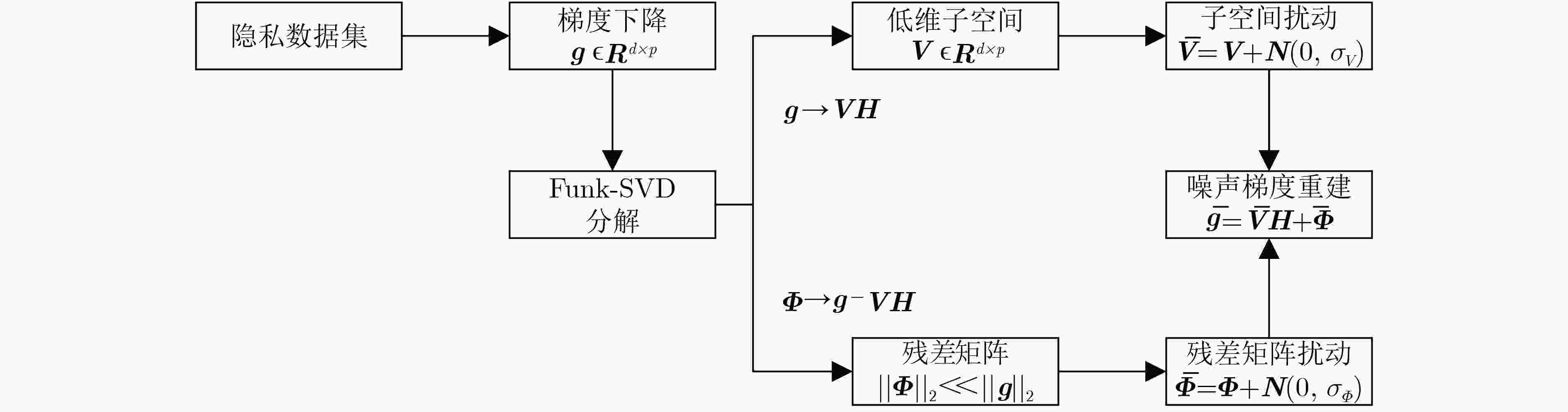
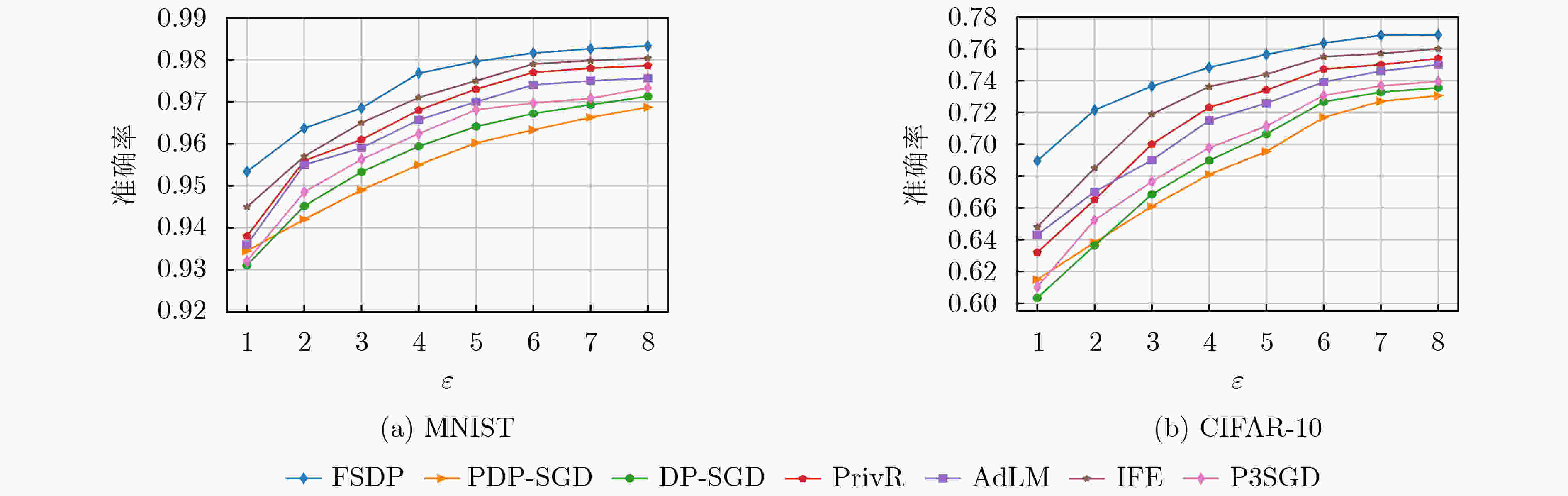
摘要: 深度神经网络梯度下降过程中存在较大的梯度冗余,应用差分隐私机制抵御成员推理攻击时,会引入过量噪声。针对上述问题,该文利用Funk-SVD矩阵分解算法将梯度矩阵分解,分别在低维特征子空间矩阵和残差矩阵中添加噪声,利用梯度重构过程消除冗余梯度噪声。重新计算分解矩阵范数并结合平滑敏感度降低噪声规模。同时根据输入特征与输出相关性,将更多隐私预算分配给相关系数大的特征以提高训练精度。最后,根据分解矩阵范数均值提出一种自适应梯度剪裁算法以解决收敛缓慢的问题。算法利用时刻统计计算了在多种优化策略下的累计隐私损失。在标准数据集MNIST和CIFAR-10上验证了该文算法更有效地弥补了与非隐私模型之间的差距。Abstract: Gradient redundancy exists in the process of deep neural network gradient descent. When differential privacy mechanism is applied to resist member inference attack, excessive noise will be introduced. So, the gradient matrix is decomposed by Funk-SVD algorithm and noise is added to the low-dimensional eigen subspace matrix and residual matrix respectively. The redundant gradient noise is eliminated in the gradient reconstruction process. The decomposition matrix norm is recalculated and the smoothing sensitivity is combined to reduce the noise scale. At the same time, according to the correlation between input features and output features, more privacy budget is allocated to features with large correlation coefficients to improve the training accuracy. The noise scale is reduced by recalculating the decomposition matrix norm and the smoothing sensitivity. Moment accountant is used to calculate the cumulative privacy loss under multiple optimization strategies. The results show that Deep neural networks under differential privacy based on Funk-SVD (FSDP) can bridge the gap with the non-privacy model more effectively on MNIST and CIFAR-10.
-
表 1 自适应梯度剪裁算法
输入: 当前批次样本的梯度$ {\boldsymbol{S}} = {\rm{\{ }}{\boldsymbol{g}}({{\boldsymbol{x}}_1}),{\boldsymbol{g}}({{\boldsymbol{x}}_2}),\cdots,{\boldsymbol{g}}({{\boldsymbol{x}}_L}){\rm{\} }} $, 噪声规模$ {\sigma _{\boldsymbol{V}}} $, $ {\sigma _{\boldsymbol{\varPhi }}} $.
输出: 自适应剪裁阈值$ {C_{\boldsymbol{g}}} $, $ {C_{\boldsymbol{V}}} $, $ {C_{\boldsymbol{\varPhi }}} $.(1) $ {\boldsymbol{g}''}({{\boldsymbol{x}}_i}) \to \{ {\boldsymbol{g}}({{\boldsymbol{x}}_i}) \in {\boldsymbol{S}}|{\mu _{\boldsymbol{g}}} - 3{\sigma _{\boldsymbol{g}}} \le ||{\boldsymbol{g}}({{\boldsymbol{x}}_i})|{|_2} \le {\mu _{\boldsymbol{g}}} + 3{\sigma _{\boldsymbol{g}}}\} $//异常值剔除
(2) $ {\boldsymbol{g}''}({{\boldsymbol{x}}_i}) \to {\boldsymbol{V}''}({{\boldsymbol{x}}_i}){\boldsymbol{H}''}({{\boldsymbol{x}}_i}) $, $ {\boldsymbol{\varPhi }''}({{\boldsymbol{x}}_i}) \to {\boldsymbol{g}''}({{\boldsymbol{x}}_i}) - {\boldsymbol{V}''}({{\boldsymbol{x}}_i}){\boldsymbol{H}''}({{\boldsymbol{x}}_i}) $//分解梯度矩阵,计算残差矩阵
(3) ${C_{\boldsymbol{V} } } \to \dfrac{1}{ {|L'|} }\sum\limits_i^{} {(||{\boldsymbol{V}''}({ {\boldsymbol{x} }_i}) + N(0,\sigma _{\boldsymbol{V} }^2{\boldsymbol{I} })|{|_2} } )$, $ \overline {{\boldsymbol{V}''}} ({{\boldsymbol{x}}_i}) \to {\boldsymbol{V}''}({{\boldsymbol{x}}_i}) + N(0,\sigma _{\boldsymbol{V}}^2{\boldsymbol{I}}) $;
${C_{\boldsymbol{\varPhi } } } \to \dfrac{1}{ {|L'|} }\sum\limits_i^{} {(||{\boldsymbol{\varPhi }''}({ {\boldsymbol{x} }_i}) + N(0,\sigma _{\boldsymbol{\varPhi } }^2{\boldsymbol{I} }))|{|_2} }$, $ \overline {{\boldsymbol{\varPhi ''}}} ({{\boldsymbol{x}}_i}){\rm{ = }}{\boldsymbol{\varPhi }''}({{\boldsymbol{x}}_i}) + N(0,\sigma _{\boldsymbol{\varPhi }}^2{\boldsymbol{I}})) $//特征矩阵${\boldsymbol{V}}$和残差矩阵$ {\boldsymbol{\varPhi }} $对应剪裁阈值
(4) $\overline {{\boldsymbol{g}''}} ({{\boldsymbol{x}}_i}) \to \overline {{\boldsymbol{V}''}} ({{\boldsymbol{x}}_i}){\boldsymbol{H}''}({{\boldsymbol{x}}_i}) + \overline {{\boldsymbol{\varPhi }''}} ({{\boldsymbol{x}}_i})$, $ {C_{\boldsymbol{g}}} \to \frac{1}{{|L'|}}\sum\limits_i^{} {||\overline {{\boldsymbol{g}''}} ({{\boldsymbol{x}}_i})|{|_2}} $//噪声梯度重建并计算梯度剪裁阈值
(5) 返回梯度剪裁阈值$ {C_{\boldsymbol{g}}} $, $ {C_{\boldsymbol{V}}} $, $ {C_{\boldsymbol{\varPhi }}} $表 2 基于Funk-SVD的深度神经网络差分隐私保护算法 (FSDP)
输入: 训练数据集$D = \{ { {\boldsymbol{x} }_1},{ {\boldsymbol{x} }_2},\cdots,{ {\boldsymbol{x} }_n}\}$, 学习率$\eta $, batch样本数量$ L $, 损失函数$ \ell ({{\boldsymbol{\omega }}_t},{{\boldsymbol{x}}_i}) $, batch数量$T$, 给定隐私预算${\varepsilon _0}$.
输出: 参数${{\boldsymbol{\omega }}_t}$.(1) 计算特征j隐私预算: ${\varepsilon _j}$
(2) for $t \in [T]$:
(3) 由抽样概率$L/N$随机选取样本集${L_t}$
(4) 根据表1算法计算当前批次剪裁阈值$ {C_{\boldsymbol{g}}} $, $ {C_{\boldsymbol{V}}} $, $ {C_{\boldsymbol{\varPhi }}} $
(5) for $i \in {L_t}$:
(6) $ {{\boldsymbol{g}}_t}({{\boldsymbol{x}}_i}) \to {\nabla _\omega }\ell ({\omega _t},{{\boldsymbol{x}}_i}) \to {\boldsymbol{VH}}{\rm{ + }}{\boldsymbol{\varPhi }} $//做Funk-SVD矩阵分解
(7) $ \sigma _j^{\boldsymbol{V}} \ge \sqrt {2\ln (1.25/\delta )} \frac{{S_{\boldsymbol{V}}^*(f,D)}}{{{\varepsilon _j}}} $, $\sigma _j^{\boldsymbol{\varPhi } } \ge \sqrt {2\ln (1.25/\delta )} \dfrac{ {S_{\boldsymbol{\varPhi } }^*(f,D)} }{ { {\varepsilon _j} } }$//计算噪声规模
(8) $ {{\boldsymbol{z}}^{\boldsymbol{V}}} \sim N(0,{(\sigma _j^{\boldsymbol{V}}{C_{\boldsymbol{V}}})^2}{{\boldsymbol{I}}_{k \times k}}) $: $ \overline {\boldsymbol{V}} \to {\boldsymbol{V}} + {{\boldsymbol{z}}^{\boldsymbol{V}}} $//扰动特征矩阵
(9) $ {{\boldsymbol{z}}^{\boldsymbol{\varPhi }}} \sim N(0,{(\sigma _j^{\boldsymbol{\varPhi }}{C_{\boldsymbol{\varPhi }}})^2}{{\boldsymbol{I}}_{p \times p}}) $: $ \overline {\boldsymbol{\varPhi }} \to {\boldsymbol{\varPhi }} + {{\boldsymbol{z}}^{\boldsymbol{\varPhi }}} $//扰动残差矩阵
(10) $ \overline {{{\boldsymbol{g}}_t}} ({{\boldsymbol{x}}_i}) \to \overline {\boldsymbol{V}} ({{\boldsymbol{x}}_i}){\boldsymbol{H}}({{\boldsymbol{x}}_i}) + \overline {\boldsymbol{\varPhi }} ({{\boldsymbol{x}}_i}) $//梯度重建
(11) end for
(12) $\widetilde { { {\boldsymbol{g} }_t} }({ {\boldsymbol{x} }_i}) \to \dfrac{1}{ { {\rm{|} }L{\rm{|} } } }\displaystyle\sum\limits_{ { {\boldsymbol{x} }_i} \in {L_t} } {(\overline { { {\boldsymbol{g} }_t} } ({ {\boldsymbol{x} }_i})/\max (1,||\overline { { {\boldsymbol{g} }_t} } ({ {\boldsymbol{x} }_i})|{|_2}/{C_{\boldsymbol{g} } }))}$//梯度剪裁
(13) 参数更新: ${{\boldsymbol{\omega }}_{t{\rm{ + }}1}} \to {{\boldsymbol{\omega }}_t}{\rm{ - }}\eta \widetilde {{{\boldsymbol{g}}_t}}({{\boldsymbol{x}}_i})$
(14) 计算隐私损失: $\varepsilon > {\varepsilon _0}$, 则结束循环
(15) end for表 3 不同特征向量数量k的训练精度(%)
数据集 隐私预算 k 10 50 200 500 1000 MNIST $ (2,{10^{ - 5}}) $ 96.12 96.37 96.41 96.39 96.07 $ (4,{10^{ - 5}}) $ 97.33 97.68 97.72 97.69 97.35 $ (8,{10^{ - 5}}) $ 98.16 98.33 98.35 98.38 97.89 CIFAR-10 $ (2,{10^{ - 5}}) $ 71.59 72.15 72.16 72.32 71.26 $ (4,{10^{ - 5}}) $ 73.95 74.83 74.87 74.93 74.05 $ (8,{10^{ - 5}}) $ 75.77 76.88 76.89 76.96 76.14 表 4 隐私损失对比
数据集 $\varepsilon $ Epochs DP-SGD PDP-SGD P3SGD 本文 MNIST 4.4 25 1.93 2.11 1.88 1.96 50 2.71 2.87 2.65 2.82 1.3 25 0.76 0.79 0.71 0.79 50 1.09 1.11 1.04 1.11 CIFAR-10 4.4 25 0.72 0.89 0.63 0.79 50 0.81 0.93 0.76 0.88 1.3 25 0.25 0.28 0.21 0.28 50 0.31 0.39 0.30 0.35 表 5 算法中各结构对训练精度(%)的影响
模型 MNIST CIFAR-10 (2, 10–5) (4, 10–5) (8, 10–5) (2, 10–5) (4, 10–5) (8, 10–5) DP-SGD 94.52 95.94 97.13 63.63 68.98 73.55 FSDP-M 95.37 96.64 97.51 67.24 71.32 74.68 FSDP-S 95.63 96.98 97.85 68.74 72.49 75.54 FSDP-R 96.18 97.51 98.21 71.29 74.25 76.54 FSDP-C 95.45 96.81 97.73 67.89 71.91 75.21 FSDP 96.37 97.68 98.33 72.15 74.83 76.88 -
[1] 刘睿瑄, 陈红, 郭若杨, 等. 机器学习中的隐私攻击与防御[J]. 软件学报, 2020, 31(3): 866–892. doi: 10.13328/j.cnki.jos.005904LIU Ruixuan, CHEN Hong, GUO Ruoyang, et al. Survey on privacy attacks and defenses in machine learning[J]. Journal of Software, 2020, 31(3): 866–892. doi: 10.13328/j.cnki.jos.005904 [2] NASR M, SHOKRI R, and HOUMANSADR A. Comprehensive privacy analysis of deep learning: Passive and active white-box inference attacks against centralized and federated learning[C]. 2019 IEEE Symposium on Security and Privacy, San Francisco, USA, 2019: 739–753. doi: 10.1109/SP.2019.00065. [3] HITAJ B, ATENIESE G, and PEREZ-CRUZ F. Deep models under the GAN: Information leakage from collaborative deep learning[C]. The 2017 ACM SIGSAC Conference on Computer and Communications Security, New York, USA, 2017: 603–618. [4] JUUTI M, SZYLLER S, MARCHAL S, et al. PRADA: Protecting against DNN model stealing attacks[C]. 2019 IEEE European Symposium on Security and Privacy (EuroS&P), Stockholm, Sweden, 2019: 512–527. [5] 冯登国, 张敏, 叶宇桐. 基于差分隐私模型的位置轨迹发布技术研究[J]. 电子与信息学报, 2020, 42(1): 74–88. doi: 10.11999/JEIT190632FENG Dengguo, ZHANG Min, and YE Yutong. Research on differentially private trajectory data publishing[J]. Journal of Electronics &Information Technology, 2020, 42(1): 74–88. doi: 10.11999/JEIT190632 [6] ABADI M, CHU A, GOODFELLOW I, et al. Deep learning with differential privacy[C]. The 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, The Republic of Austria, 2016: 308–318. [7] XU Chugui, REN Ju, ZHANG Deyu, et al. GANobfuscator: Mitigating information leakage under GAN via differential privacy[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(9): 2358–2371. doi: 10.1109/TIFS.2019.2897874 [8] PHAN N, VU M N, LIU Yang, et al. Heterogeneous Gaussian mechanism: Preserving differential privacy in deep learning with provable robustness[C]. The Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 2019: 4753–4759. [9] PHAN N, WU Xintao, HU Han, et al. Adaptive Laplace mechanism: Differential privacy preservation in deep learning[C]. 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, USA, 2017: 385–394. [10] GONG Maoguo, PAN Ke, and XIE Yu. Differential privacy preservation in regression analysis based on relevance[J]. Knowledge-Based Systems, 2019, 173: 140–149. doi: 10.1016/j.knosys.2019.02.028 [11] ADESUYI T A and KIM B M. Preserving privacy in convolutional neural network: An ∈-tuple differential privacy approach[C]. 2019 IEEE 2nd International Conference on Knowledge Innovation and Invention (ICKII), Seoul, South Korea, 2019: 570–573. [12] WU Bingzhe, ZHAO Shiwan, SUN Guangyu, et al. P3SGD: Patient privacy preserving SGD for regularizing deep CNNs in pathological image classification[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 2094–2103. [13] ZHOU Yingxue, WU Zhiwei, and BANERJEE A. Bypassing the ambient dimension: Private SGD with gradient subspace identification[EB/OL]. https://arxiv.org/abs/2007.03813,2020. [14] SUN Lichao, ZHOU Yingbo, YU P S, et al. Differentially private deep learning with smooth sensitivity[EB/OL]. https://arxiv.org/abs/2003.00505, 2020. [15] THAKURTA A. Beyond worst case sensitivity in private data analysis[M]. KAO M Y. Encyclopedia of Algorithms. Boston: Springer, 2016: 192–199. [16] XU Jincheng and DU Qingfeng. Adversarial attacks on text classification models using layer-wise relevance propagation[J]. International Journal of Intelligent Systems, 2020, 35(9): 1397–1415. doi: 10.1002/int.22260 -





 下载:
下载:


 下载:
下载:
