Fast Algorithm of Image Selective Segmentation Model Based on Convex Relaxation
-
摘要: 针对基于测地距离的图像选择性分割模型非凸的缺陷,该文结合凸松弛方法,提出凸松弛的选择性分割模型,并通过证明,给出凸松弛模型的解与原模型解之间的关系。然后,应用交替方向乘子法(ADMM),设计凸松弛模型的数值求解算法,并给出了该算法的收敛性。数值实验结果表明:该文所提算法的收敛速度不仅大大优于求解原模型的加性算子分裂算法,而且分割结果也更精确。Abstract: In view of the non-convex defect of the image selective segmentation model based on geodesic distance, a convex selective segmentation model by convex relaxation is proposed. The relationship between the solution of the convex model and that of the original model is given. Then by incorporating the Alternating Direction Method of Multipliers (ADMM), this paper designs a fast algorithm for numerically solving the convex model and gives the convergence of the algorithm. Finally, numerical experimental results show that convergence speed of the proposed algorithm is much better than the original algorithm based on the additive operator splitting method, and the segmentation results of the proposed algorithm are more accurate.
-
表 1 本文算法的求解流程
初始赋值:${{\boldsymbol{d}}^0} = 0$,${{\boldsymbol{\lambda}} ^0} = 0$,$ {u^0} $取决于标记集$ M $ 迭代:更新$ {u^{k + 1}} $,${{\boldsymbol{d}}^{k + 1} }$,${{\boldsymbol{\lambda}} ^{k + 1} }$ ${ {\boldsymbol{d} }^{k + 1} } = {\text{shrink} }\left(\nabla {u^k} + \dfrac{ { {{\boldsymbol{\lambda}} ^k} } }{\beta },\beta \right)$, ${u^{k + \frac{1}{2} } } = {\text{GS} }({{\boldsymbol{d}}^{k + 1} },{{\boldsymbol{\lambda}} ^k})$,${u^{k + 1} } = \Pr {\text{o} }{ {\text{j} }_\varGamma }({u^{k + \frac{1}{2} } })$, ${ {\boldsymbol{\lambda} } ^{k + 1} } = { {\boldsymbol{\lambda} } ^k} + \beta (\nabla {u^{k + 1} } - {{\boldsymbol{d}}^{k + 1} })$, ${\varSigma ^{ {\text{k} } + 1} } = \left\{ {x \in \varOmega |{u^{k + 1} }(x) \ge \xi } \right\}$对于任意$ \xi \in [0,1] $,
${c_1}^{k + 1} = \dfrac{ {\displaystyle\int\limits_\varOmega {z{u^{k + 1} }{\rm{d}}\varOmega } } }{ {\displaystyle\int\limits_\varOmega { {u^{k + 1} }{\rm{d}}\varOmega } } }$ ,${c_2}^{k + 1} = \dfrac{ {\displaystyle\int\limits_\varOmega {z(1 - {u^{k + 1} }){\rm{d}}\varOmega } } }{ {\displaystyle\int\limits_\varOmega {(1 - {u^{k + 1} }){\rm{d}}\varOmega } } }$,迭代终止条件:$\dfrac{{{\text{||}}{u^{k + 1}} - {u^k}||}}{{||{u^k}||}} \lt {\text{Tol}}$。 表 2 本文算法分割图像的参数
$ {\lambda _1} $ ,$ {\lambda _2} $ 和$ \theta $ 的值表 3 图2中分割结果的DSC(%)、HD值、迭代收敛步数及收敛时间(s)
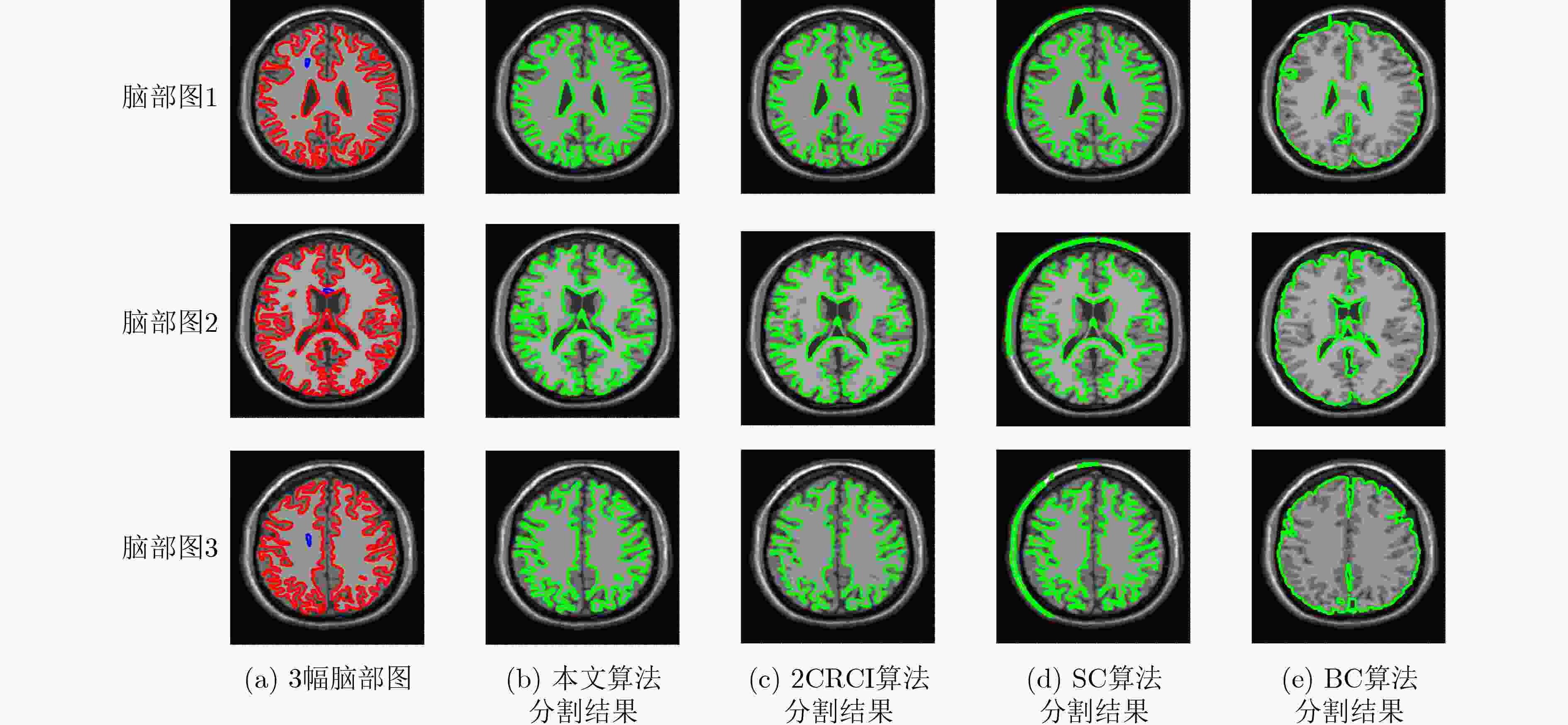
图像 脑部图1 脑部图2 脑部图3 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 BC算法 77.78 3.8190 400 112.31 76.98 4.2858 380 107.57 74.95 3.7832 380 106.14 SC算法 92.48 2.2155 484 73.00 85.62 3.1259 500 74.86 86.41 2.7437 500 84.63 CRCI算法 94.62 1.7000 600 88.85 93.03 2.1251 4783 78.46 92.87 1.8523 619 89.45 本文算法 96.36 1.2660 24 7.77 94.40 1.8216 38 12.16 93.91 1.6728 32 10.03 表 4 图3中分割结果的DSC(%)、HD值、迭代收敛步数及收敛时间(s)
图像 σ=0.01 σ=0.02 σ=0.03 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 BC算法 88.92 0.9940 180 45.40 88.67 1.0917 330 97.94 88.28 1.2310 600 153.86 SC算法 93.97 2.2062 715 107.62 83.54 2.0744 850 121.29 92.53 2.5350 900 126.69 CRCI算法 96.43 1.1073 450 64.44 96.33 1.1073 450 62.44 96.39 1.1746 281 43.07 本文算法 96.43 1.0870 36 13.21 96.38 1.1336 34 9.13 96.43 1.0990 41 11.43 表 5 图4中分割结果的DSC(%)、HD值、迭代收敛步数及收敛时间(s)
图像 CT图像1 CT图像2 CT图像3 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 BC算法 84.99 1.5763 25 10.20 69.11 1.8017 20 7.29 75.73 0.8411 18 6.79 SC算法 97.33 0.6366 720 96.06 90.37 0.4213 1050 147.80 95.00 0.1860 850 111.86 CRCI算法 97.08 0.6119 912 129.51 86.27 0.1729 4797 800.83 95.55 0.1719 1787 313.94 本文算法 98.39 0.5968 75 20.12 97.90 0.2929 66 17.08 98.25 0.1284 54 13.88 表 6 图5中分割结果的DSC(%)、HD值、迭代收敛步数及收敛时间(s)
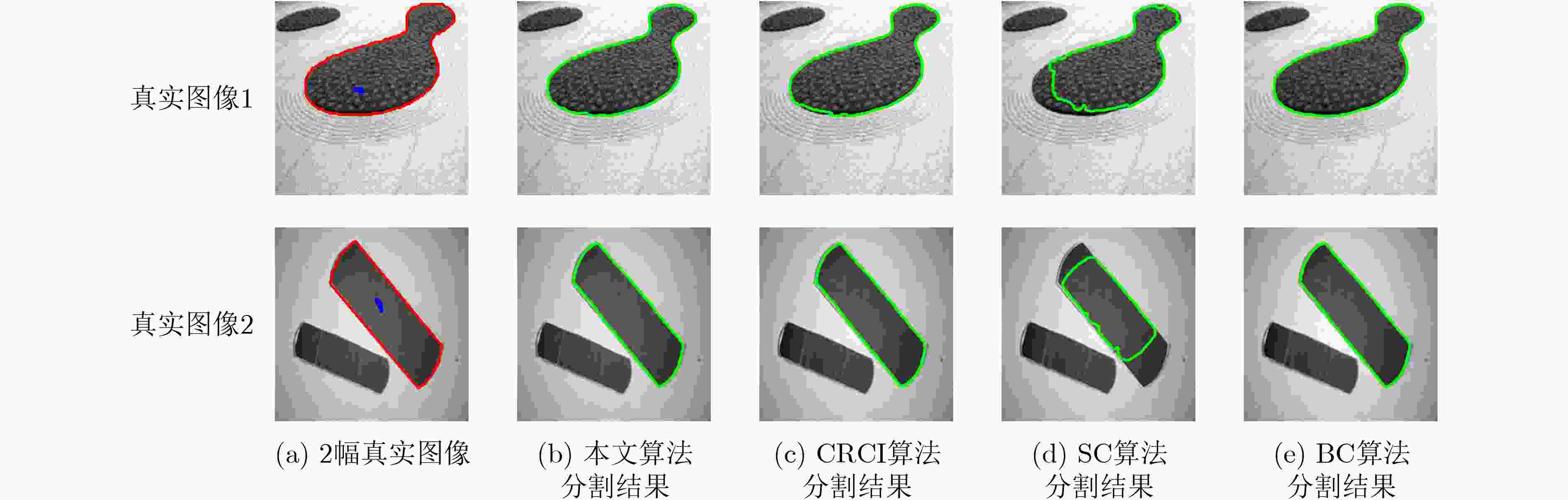
图像 真实图像1 真实图像2 DSC HD 迭代收敛步数 收敛时间 DSC HD 迭代收敛步数 收敛时间 BC算法 98.52 0.5298 300 89.13 98.10 0.6631 100 22.20 SC算法 90.48 1.7070 700 97.15 81.03 2.5656 800 114.58 CRCI算法 97.80 0.6896 335 47.77 97.61 0.7284 174 18.78 本文算法 98.06 0.6304 43 11.20 98.00 0.6961 20 6.54 -
[1] KASS M, WITKIN A, and TERZOPOULOS D. Snakes: Active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321–331. doi: 10.1007/BF00133570 [2] CASELLES V, KIMMEL R, and SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61–79. doi: 10.1023/A:1007979827043 [3] MUMFORD D and SHAH J. Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on Pure and Applied Mathematics, 1989, 42(5): 577–685. doi: 10.1002/cpa.3160420503 [4] CHAN T F and VESE L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266–277. doi: 10.1109/83.902291 [5] BADSHAH N and CHEN Ke. Image selective segmentation under geometrical constraints using an active contour approach[J]. Communications in Computational Physics, 2010, 7(4): 759–778. doi: 10.4208/cicp.2009.09.026 [6] LE GUYADER C and GOUT C. Geodesic active contour under geometrical conditions: Theory and 3D applications[J]. Numerical Algorithms, 2008, 48(1/3): 105–133. doi: 10.1007/s11075-008-9174-y [7] RADA L and CHEN Ke. Improved selective segmentation model using one level-set[J]. Journal of Algorithms & Computational Technology, 2013, 7(4): 509–540. doi: 10.1260/1748-3018.7.4.509 [8] SPENCER J and CHEN Ke. A convex and selective variational model for image segmentation[J]. Communications in Mathematical Sciences, 2015, 13(6): 1453–1472. doi: 10.4310/CMS.2015.v13.n6.a5 [9] ROBERTS M, CHEN Ke, and IRION K L. A convex geodesic selective model for image segmentation[J]. Journal of Mathematical Imaging and Vision, 2019, 61(4): 482–503. doi: 10.1007/s10851-018-0857-2 [10] ALI H, FAISAL S, CHEN Ke, et al. Image-selective segmentation model for multi-regions within the object of interest with application to medical disease[J]. The Visual Computer, 2021, 37(5): 939–955. doi: 10.1007/s00371-020-01845-1 [11] KAPURIYA B R, PRADHAN D, and SHARMA R. Geometric constraints based selective segmentation for vector valued images[C]. The IEEE 2020 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 2020: 1–5. [12] ZHANG Jianjun and NAGY J G. An effective alternating direction method of multipliers for color image restoration[J]. Applied Numerical Mathematics, 2021, 164: 43–56. doi: 10.1016/j.apnum.2020.07.008 [13] PADCHAROEN A, KITKUAN D, KUMAM P, et al. Accelerated alternating minimization algorithm for Poisson noisy image recovery[J]. Inverse Problems in Science and Engineering, 2020, 28(7): 1031–1056. doi: 10.1080/17415977.2019.1709454 [14] CHAN T F, ESEDOGLU S, and NIKOLOVA M. Algorithms for finding global minimizers of image segmentation and denoising models[J]. SIAM Journal on Applied Mathematics, 2006, 66(5): 1632–1648. doi: 10.1137/040615286 [15] VAASSEN F, HAZELAAR C, VANIQUI A, et al. Evaluation of measures for assessing time-saving of automatic organ-at-risk segmentation in radiotherapy[J]. Physics and Imaging in Radiation Oncology, 2020, 13: 1–6. doi: 10.1016/j.phro.2019.12.001 [16] LIU Qiong, PENG Hao, CHEN Jifeng, et al. Design and implementation of parallel algorithm for image matching based on Hausdorff Distance[J]. Microprocessors and Microsystems, 2021, 82: 103919. doi: 10.1016/j.micpro.2021.103919 -





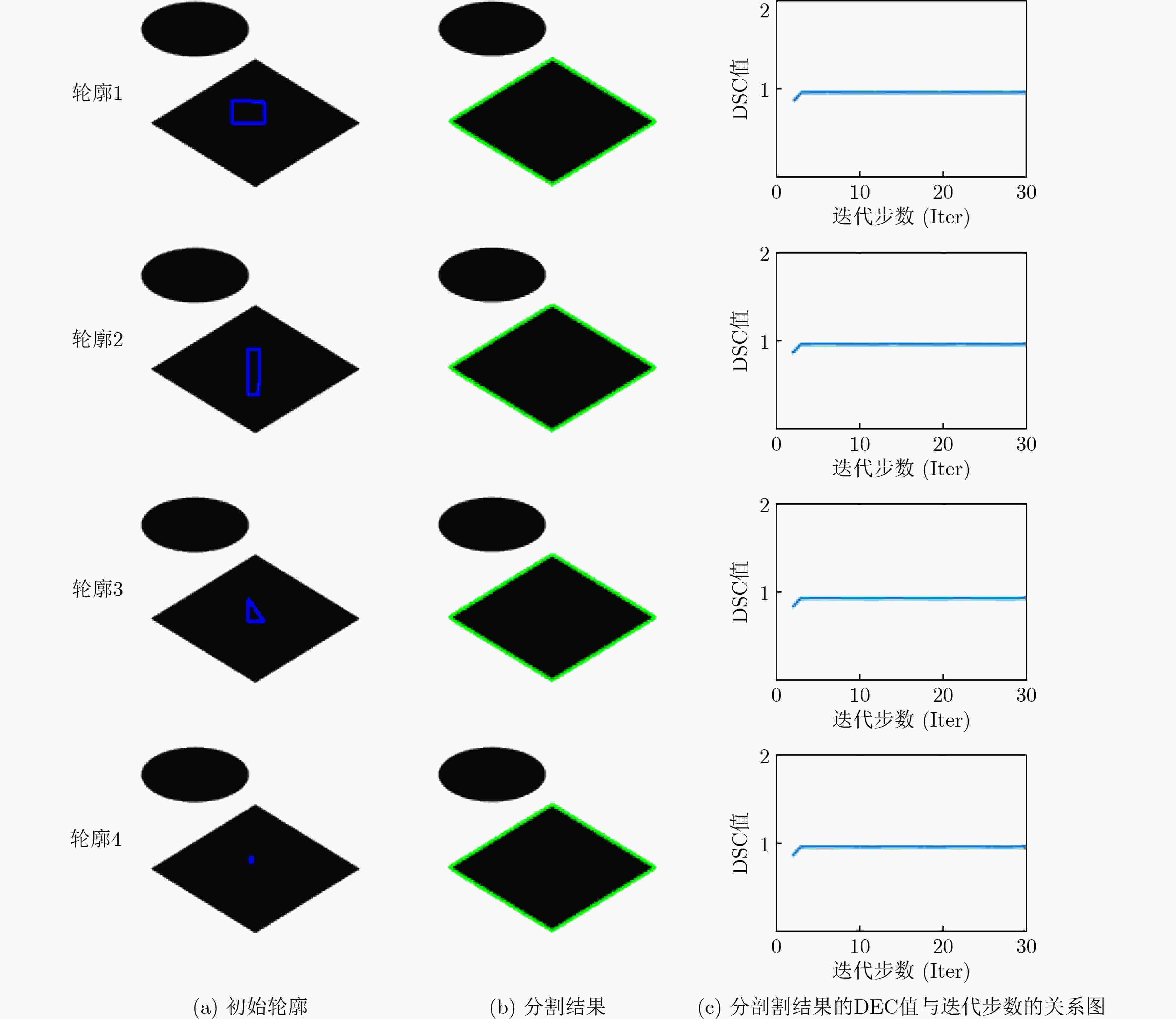
 下载:
下载:

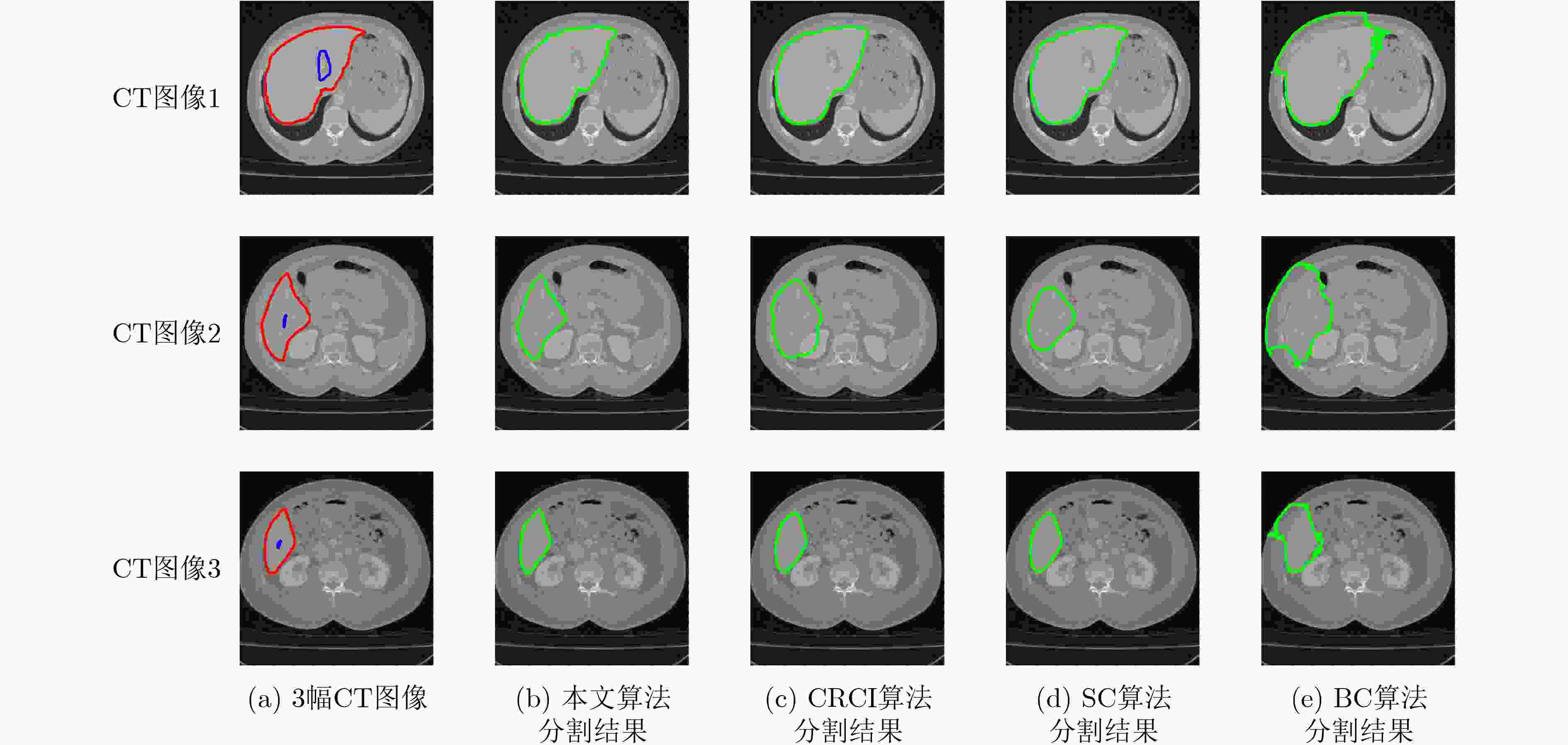





 下载:
下载:
