图强化典型相关分析及在图像识别中的应用

苏树智; 谢军; 平昕瑞; 高鹏连

doi:10.11999/JEIT210154

图强化典型相关分析及在图像识别中的应用

doi: 10.11999/JEIT210154

苏树智^{1, 2, ,},
谢军¹,
平昕瑞³,
高鹏连¹

1.
安徽理工大学计算机科学与工程学院淮南 232001
2.
合肥综合性国家科学中心能源研究院(安徽省能源实验室) 合肥 230031
3.
安徽理工大学数学与大数据学院淮南 232001

基金项目: 国家自然科学基金(61806006)，中国博士后科学基金(2019M660149)，合肥综合性国家科学中心能源研究院项目(19KZS203)

详细信息

作者简介:
苏树智：男，1987年生，副教授，研究方向为多模态模式识别

谢军：男，1996年生，硕士生，研究方向为模式识别

平昕瑞：男，1994年生，硕士生，研究方向为多模态信息融合、数据处理

高鹏连：男，1996年生，硕士生，研究方向为模式识别

通讯作者:
苏树智　sushuzhi@foxmail.com

中图分类号: TN911.73; TP391.4
计量
- 文章访问数: 947
- HTML全文浏览量: 395
- PDF下载量: 117
- 被引次数: 0
出版历程
- 收稿日期: 2021-02-18
- 修回日期: 2021-05-20
- 网络出版日期: 2021-06-04
- 刊出日期: 2021-11-23

Graph Enhanced Canonical Correlation Analysis and Its Application to Image Recognition

Shuzhi SU^{1, 2
, ,},
Jun XIE¹,
Xinrui PING³,
Penglian GAO¹

1.
School of Computer Science and Engineering, Anhui University of Science & Technology, Huainan 232001, China
2.
Institute of Energy, Hefei Comprehensive National Science Center, Hefei 230031, China
3.
School of Mathematics and Big Data, Anhui University of Science & Technology, Huainan 232001, China

Funds: The National Natural Science Foundation of China (61806006), The China Postdoctoral Science Foundation (2019M660149), The Institute of Energy, Hefei Comprehensive National Science Center (19KZS203)

摘要

摘要: 典型相关分析(CCA)作为一种传统特征提取算法已经成功应用于模式识别领域，其旨在找到使两组模态数据间相关性最大的投影方向，但其本身为一种无监督的线性方法，无法利用数据内在的几何结构和监督信息，难以处理高维非线性数据。为此该文提出一种新的非线性特征提取算法，即图强化典型相关分析(GECCA)。该算法利用数据中的不同成分构建多个成分图，有效保留了数据间的复杂流形结构，采用概率评估的方法使用类标签信息，并通过图强化的方式将几何流形和监督信息融合嵌入到典型相关分析框架。为了对该算法进行评估，分别在人脸和手写体数字数据集上设计了针对性实验，良好的实验结果显示出该算法在图像识别中的优势。
- 模式识别 /
- 典型相关分析 /
- 成分图 /
- 概率评估
Abstract: As a traditional feature extraction algorithm, Canonical Correlation Analysis (CCA) has been excellently used for the field of pattern recognition. It aims to find the projection direction that makes the maximum of the correlation between two groups of modal data. However, since the algorithm is an unsupervised linear method, it can not use intrinsic geometry structures and supervised information hidden in data, which will cause difficulty in dealing with high-dimensional nonlinear data. Therefore, this paper proposes a new nonlinear feature extraction algorithm, namely Graph Enhanced Canonical Correlation Analysis (GECCA). The algorithm uses different components of the data to construct multiple component graphs, which retains effectively the complex manifold structures between the data. The algorithm utilizes the probability evaluation method to use class label information, and the graph enhancement method is utilized to integrate the geometry manifolds and the supervised information into the typical correlation analysis framework. Targeted experiments are designed on the face and handwritten digital image datasets to evaluate the algorithm. Good experimental results show the advantages of GECCA in image recognition.
- Pattern recognition /
- Canonical Correlation Analysis (CCA) /
- Component graph /
- Probability evaluation

HTML全文

图 1 成分图权重矩阵流程图

下载: 全尺寸图片幻灯片

图 2 XM2VTS部分人脸图像

下载: 全尺寸图片幻灯片

图 3 在XM2VTS人脸数据集上识别率随维度变化情况

下载: 全尺寸图片幻灯片

图 4 在Semeion数据集中每次随机实验的最佳识别率

下载: 全尺寸图片幻灯片

表 1 GECCA的算法步骤

算法：图强化典型相关分析
(1) 输入:{X,Y},C_x和C_y。
(2)通过式(12)和式(13)构建图强化矩阵M_x和M_y。利用式(16)构建类拉普拉斯矩阵L_x, L_x, L_xy和 L_yx。
(3)构建拉格朗日乘子函数：${\boldsymbol{F} }\left( { {\boldsymbol{\alpha} } ,{\boldsymbol{\beta} } } \right) = { {\boldsymbol{\alpha} } ^{\rm{T} } }{\boldsymbol{X} }{ {\boldsymbol{L} }_{ { {xy} } } }{ {\boldsymbol{Y} }^{\rm{T} } }{\boldsymbol{\beta} } - \dfrac{ { { {{\lambda } }_1} } }{2}\left( { { {\boldsymbol{\alpha} } ^{\rm{T} } }{\boldsymbol{X} }{ {\boldsymbol{L} }_{ { {xx} } } }{ {\boldsymbol{X} }^{\rm{T} } }{\boldsymbol{\alpha} } - 1} \right) - \dfrac{ { { {{\lambda } }_2} } }{2}\left( { { {\boldsymbol{\beta} } ^{\rm{T} } }{\boldsymbol{Y} }{ {\boldsymbol{L} }_{ { {yy} } } }{ {\boldsymbol{Y} }^{\rm{T} } }{\boldsymbol{\beta} } - 1} \right)$。
(4)按照式(20)求出特征值λ和对应特征向量(α，β)。
(5)取前d个特征值对应特征向量$\left\{ {\;{ {\left[ { {\boldsymbol{\alpha} } _{ {i} }^{\rm{T} },{\boldsymbol{\beta} } _{ {i} }^{\rm{T} } } \right]}^{\rm{T} } }\; \in { { \boldsymbol{R} }^{1 \times \left( { { {p} } + { {q} } } \right)} } } \right\}_{ { {i} } = 1}^{ {d} }$。
(6)输出:${\boldsymbol{A} } = \left\{ { { {\boldsymbol{\alpha} } _1},{ {\boldsymbol{\alpha} } _2},...,{ {\boldsymbol{\alpha} } _{ {d} } } } \right\} \in { { \boldsymbol{R} }^{ { {p} } \times { {d} } } }$和${\boldsymbol{B} } = \left\{ { { {\boldsymbol{\beta} } _1},{ {\boldsymbol{\beta} } _2},\;...,{ {\boldsymbol{\beta} } _{ {d} } } } \right\} \in { { \boldsymbol{R} }^{ { {q} } \times { {d} } } }$。

下载: 导出CSV

表 2 在Semeion手写体数字数据集上的识别率及标准差

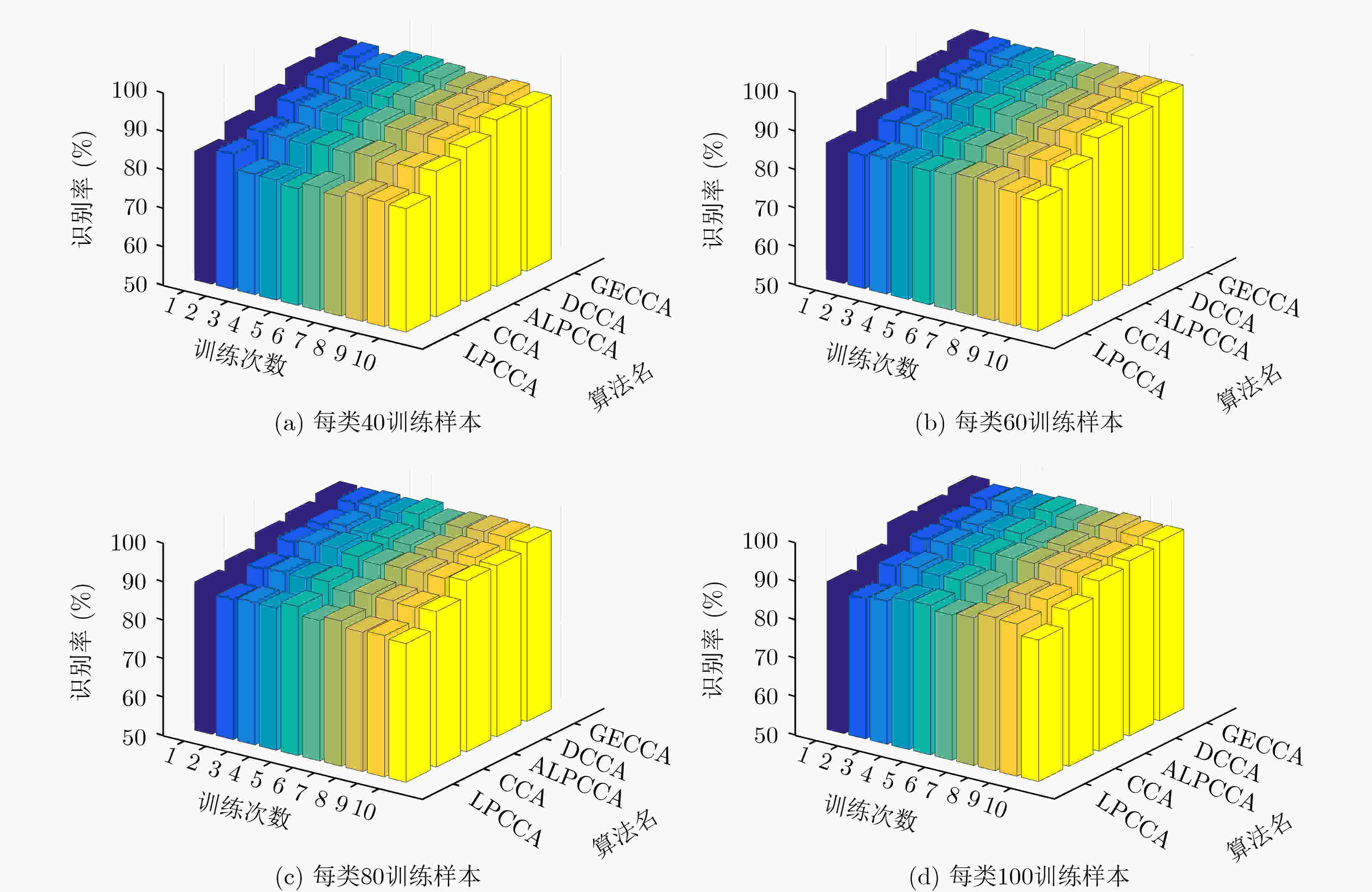
	40训练样本	60训练样本	80训练样本	100训练样本
GECCA	86.93±0.92	88.89±0.98	90.69±0.77	91.38±0.70
DCCA	85.72±1.02	87.57±1.04	89.14±0.82	80.25±0.91
ALPCCA	80.82±0.75	84.76±1.19	87.92±0.77	89.38±1.03
LPCCA	69.84±2.24	74.83±1.51	77.33±1.47	80.56±2.10
CCA	74.20±0.84	77.93±1.19	80.92±0.85	82.34±1.44
A±B：A表示平局识别率(%)，B表示标准差

下载: 导出CSV

参考文献(19)

[1]	LIU Zhonghua, LAI Zhihui, OU Weihua, et al. Structured optimal graph based sparse feature extraction for semi-supervised learning[J]. Signal Processing, 2020, 170: 107456. doi: 10.1016/j.sigpro.2020.107456
[2]	王肖锋, 孙明月, 葛为民. 基于图像协方差无关的增量特征提取方法研究[J]. 电子与信息学报, 2019, 41(11): 2768–2776. doi: 10.11999/JEIT181138 WANG Xiaofeng, SUN Mingyue, and GE Weimin. An incremental feature extraction method without estimating image covariance matrix[J]. Journal of Electronics &Information Technology, 2019, 41(11): 2768–2776. doi: 10.11999/JEIT181138
[3]	YI Shuangyan, LAI Zhihui, HE Zhenyu, et al. Joint sparse principal component analysis[J]. Pattern Recognition, 2017, 61: 524–536. doi: 10.1016/j.patcog.2016.08.025
[4]	BRO R and SMILDE A K. Principal component analysis[J]. Analytical Methods, 2014, 6(9): 2812–2831. doi: 10.1039/C3AY41907J
[5]	刘政怡, 段群涛, 石松, 等. 基于多模态特征融合监督的RGB-D图像显著性检测[J]. 电子与信息学报, 2020, 42(4): 997–1004. doi: 10.11999/JEIT190297 LIU Zhengyi, DUAN Quntao, SHI Song, et al. RGB-D image saliency detection based on multi-modal feature-fused supervision[J]. Journal of Electronics &Information Technology, 2020, 42(4): 997–1004. doi: 10.11999/JEIT190297
[6]	姜庆超, 颜学峰. 基于局部−整体相关特征的多单元化工过程分层监测[J]. 自动化学报, 2020, 46(9): 1770–1782. JIANG Qingchao and YAN Xuefeng. Hierarchical monitoring for multi-unit chemical processes based on local-global correlation features[J]. Acta Automatica Sinica, 2020, 46(9): 1770–1782.
[7]	YANG Xinghao, LIU Weifeng, LIU Wei, et al. A survey on canonical correlation analysis[J]. IEEE Transactions on Knowledge and Data Engineering, 2021, 33(6): 2349–2368. doi: 10.1109/TKDE.2019.2958342
[8]	YANG Xinghao, LIU Weifeng, TAO Dapeng, et al. Canonical correlation analysis networks for two-view image recognition[J]. Information Sciences, 2017, 385/386: 338–352. doi: 10.1016/j.ins.2017.01.011
[9]	SHEN Xiaobo, SUN Quansen, and YUAN Yunhao. Orthogonal canonical correlation analysis and its application in feature fusion[C]. The 16th International Conference on Information Fusion, Istanbul, Turkey, 2013: 151–157.
[10]	EL MADANY N E D, HE Yifeng, and GUAN Ling. Human action recognition by fusing deep features with globality locality preserving canonical correlation analysis[C]. 2017 IEEE International Conference on Image Processing, Beijing, China, 2017: 2871–2875.
[11]	ELMADANY N E D, HE Yifeng, and GUAN Ling. Information fusion for human action recognition via biset/multiset globality locality preserving canonical correlation analysis[J]. IEEE Transactions on Image Processing, 2018, 27(11): 5275–5287. doi: 10.1109/TIP.2018.2855438
[12]	WANG Fengshan and ZHANG Daoqiang. A new locality-preserving canonical correlation analysis algorithm for multi-view dimensionality reduction[J]. Neural Processing Letters, 2013, 37(2): 135–146. doi: 10.1007/s11063-012-9238-9
[13]	GAO Xizhan, NIU Sujie, and SUN Quansen. Two-directional two-dimensional kernel canonical correlation analysis[J]. IEEE Signal Processing Letters, 2019, 26(11): 1578–1582. doi: 10.1109/LSP.2019.2939986
[14]	MELZER T, REITER M, and BISCHOF H. Appearance models based on kernel canonical correlation analysis[J]. Pattern Recognition, 2003, 36(9): 1961–1971. doi: 10.1016/S0031-3203(03)00058-X
[15]	SUN Tingkai, CHEN Songcan, YANG Jingyu, et al. A supervised combined feature extraction method for recognition[C]. The IEEE International Conference on Data Mining, Pisa, Italy, 2008: 1043–1048.
[16]	GAO Lei, QI Lin, CHEN Enqing, et al. Discriminative multiple canonical correlation analysis for information fusion[J]. IEEE Transactions on Image Processing, 2018, 27(4): 1951–1965. doi: 10.1109/TIP.2017.2765820
[17]	CHEN Jia, WANG Gang, and GIANNAKIS G B. Graph multiview canonical correlation analysis[J]. IEEE Transactions on Signal Processing, 2019, 67(11): 2826–2838. doi: 10.1109/TSP.2019.2910475
[18]	CHEN Jia, WANG Gang, SHEN Yanning, et al. Canonical correlation analysis of datasets with a common source graph[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4398–4408. doi: 10.1109/TSP.2018.2853130
[19]	SU Shuzhi, FANG Xianjin, YANG Gaoming, et al. Self-balanced multi-view orthogonality correlation analysis for image feature learning[J]. Infrared Physics & Technology, 2019, 100: 44–51.