An Intelligent Decision-making Algorithm for Communication Countermeasure Jamming Resource Allocation
-
摘要: 针对战场通信对抗智能决策问题,该文基于整体对抗思想提出一种基于自举专家轨迹分层强化学习的干扰资源分配决策算法(BHJM),算法针对跳频干扰决策难题,按照频点分布划分干扰频段,再基于分层强化学习模型分级决策干扰频段和干扰带宽,最后利用基于自举专家轨迹的经验回放机制采样并训练优化算法,使算法能够在现有干扰资源特别是干扰资源不足的条件下,优先干扰最具威胁目标,获得最优干扰效果同时减少总的干扰带宽。仿真结果表明,算法较现有资源分配决策算法节约25%干扰站资源,减少15%干扰带宽,具有较大实用价值。Abstract: Considering the intelligent decision of battlefield communication countermeasure, based on the overall confrontation, a Bootstrapped expert trajectory memory replay - Hierarchical reinforcement learning - Jamming resources distribution decision - Making algorithm(BHJM) is proposed, and the algorithm for frequency hopping jamming decision problem, according to the frequency distribution, jamming spectrum is divided, based on hierarchical reinforcement learning again decision jamming spectrum and bandwidth are divided, and finally based on the bootstrapped expert trajectory memory replay mechanism, the algorithm is optimized, the algorithm can is existing resources, especially under the condition of insufficient resources, give priority to jam the most threat target, obtain the optimal jamming effect and reduce the total jamming bandwidth. The simulation results show that, compared with the existing resource allocation decision algorithms, the proposed algorithm can save 25% of the resources of jammers and 15% of the jamming bandwidth, which is of great practical value.
-
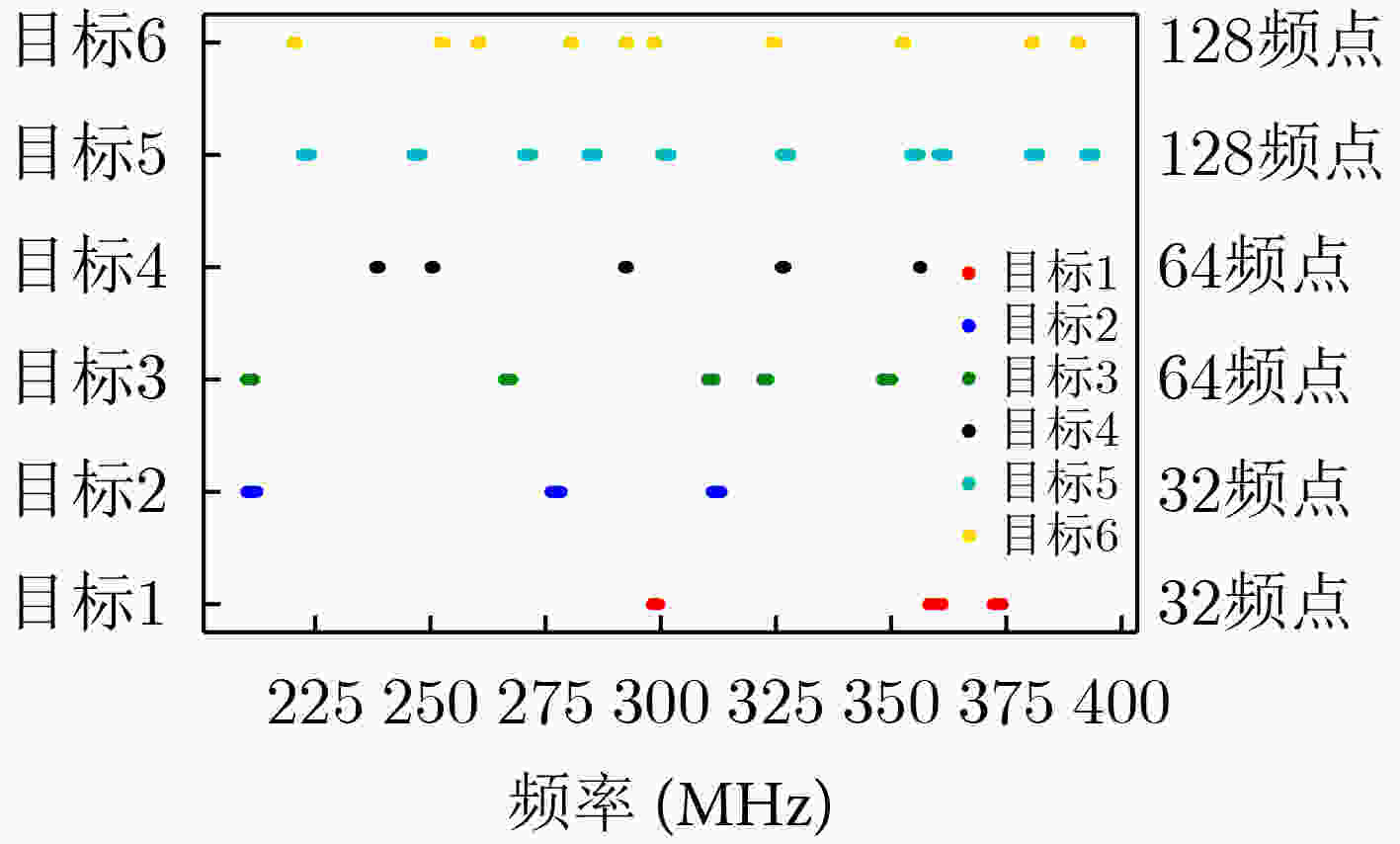
表 1 目标属性
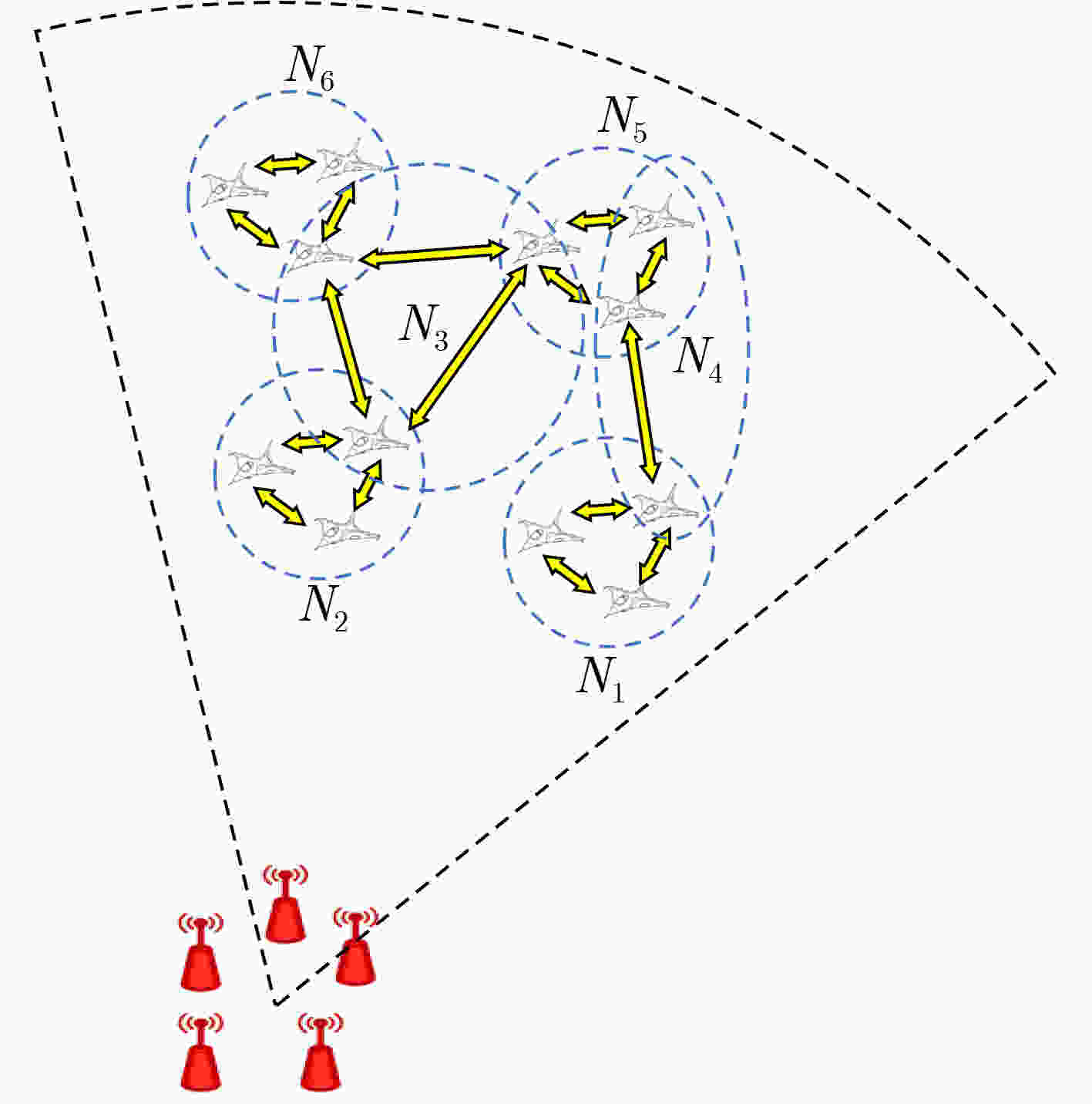
目标 属性 威胁系数 ${N_1}$ 通信网1 6 ${N_2}$ 通信网2 5 ${N_3}$ 通信网3 4 ${N_4}$ 通信网4 3 ${N_5}$ 通信网5 2 ${N_6}$ 通信网6 1 表 2 干扰资源分配算法
算法1 基于整体对抗思想的干扰资源分配算法 (1)按照威胁系数设置对目标的干扰顺序$[{T_1},{T_2},\cdots,{T_M}]$, ${T_1}$为第1目标,${T_M}$为最末目标; (2)按照干扰机最大干扰带宽${B_{\max }}$将所有目标频点按划分为多个子频段$[{J_{ {S_1} } },{J_{ {S_2} } },\cdots,{J_{ {S_Y} } }]$; Repeat: (3)给干扰机${J_1}$选择干扰频段${J_{{S_1}}}$; (4)根据频段${J_{{S_1}}}$设置干扰带宽${B_1}$,找出在带宽范围内包含${T_1}$频点数量最多的频率集,该带宽范围即为拦阻干扰带,${{\boldsymbol{P}}_1}{\rm{ = }}[{J_{{S_1}}},{B_1}]$为干扰
策略$\pi $的一部分;(5)重复步骤3和4,直至所有目标被完全阻断或干扰资源全部用完,此时共生成$K$个子干扰策略,干扰策略$\pi {\rm{ = } }[{P_1},{P_2},\cdots,{P_K}]$。 Break. 表 3 BETMR算法
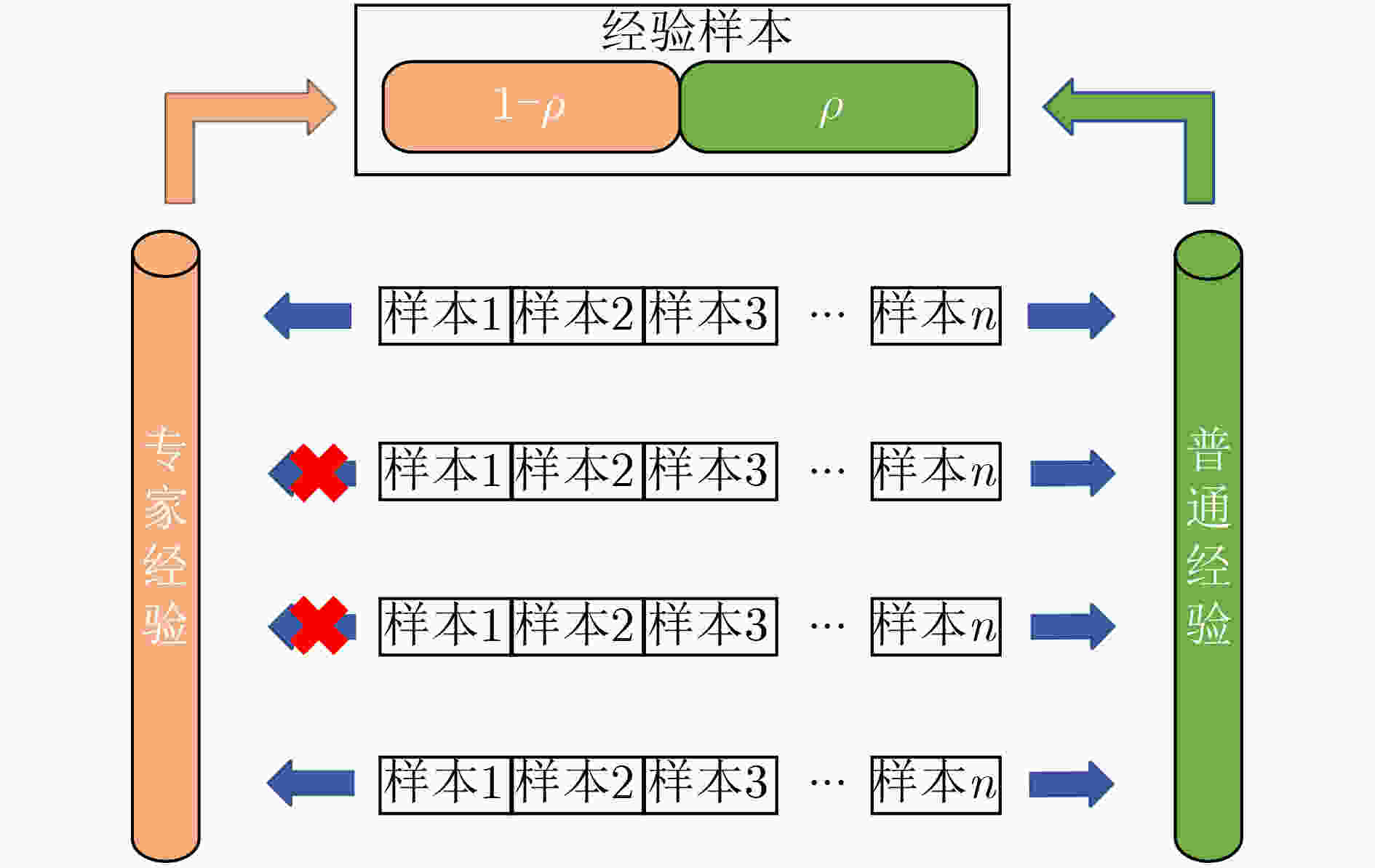
算法2 BETMR算法 (1)建立经验池${ {\boldsymbol{E} }_{ {\bf{normal} } } }$和${ {\boldsymbol{E} }_{ {\bf{expert} } } }$,初始化为空集; (2)设置初始阈值$\delta $,$\delta {\rm{ = }}{\delta _0}$; Repeat: (3)将样本$e$存入${ {\boldsymbol{E} }_{ {\bf{normal} } } }$中; (4)当回合结束: Break; (5)判断该回合样本是否满足专家轨迹条件, 若满足:将样本$e$存入${ {\boldsymbol{E} }_{ {\bf{expert} } } }$中; 若不满足:pass (6)按式(6)计算下一回合$\delta $,若$\delta $改变,重置${ {\boldsymbol{E} }_{ {\bf{expert} } } }$为空集; (7)按式(7)抽取样本${\boldsymbol{E}}$。 表 4 BHJM算法
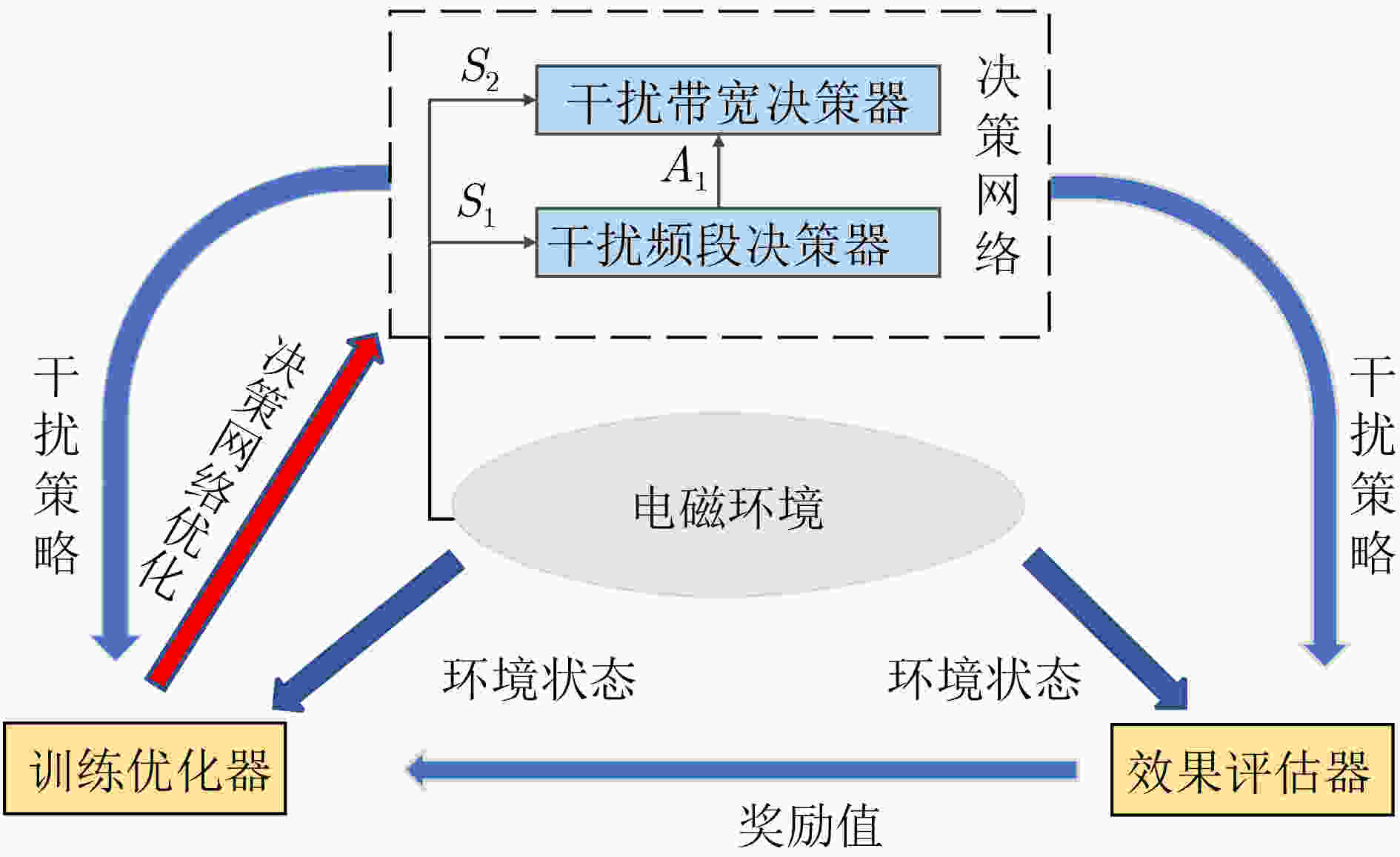
算法3 BHJM算法 (1)初始化干扰频段、带宽决策器,分别建立两个神经网络:权值参数为θ的估值神经网络和权值参数为θ-的目标神经网络; Repeat: While $j < W$: (2)目标生成器获取环境状态${S_0}$,给出干扰目标$g$; (3)干扰频段决策器获取环境状态${S_1}$,决策干扰频段即干扰动作${A_1}$; (4)干扰频段决策器获取环境状态${S_2}$,决策干扰带宽即干扰动作${A_2}$; (5)效果评估器计算奖励值${r_1}$和${r_2}$; (6)两层决策器分别按照BETMR机制存储样本${{\boldsymbol{E}}_1}$和${{\boldsymbol{E}}_2}$; (7)获取下一步环境状态${S_1}'$和${S_2}'$; (8)当完成干扰任务或干扰资源用尽: Break; (9)当前回合结束后,两层决策器分别按式(14)更新各自的估值神经网络; (10)每$L$个回合后,按式(16)、式(17)分别更新两层决策器的目标神经网络; (11)当算法训练至最优后,循环结束。 表 5 侦察目标信息
目标 威胁系数 通信距离(km) 通信发射功率(W) 干扰距离(km) ${N_1}$ 6 20 100 30 ${N_2}$ 5 20 100 50 ${N_3}$ 4 50 100 70 ${N_4}$ 3 50 100 90 ${N_5}$ 2 20 100 110 ${N_6}$ 1 20 100 130 -
[1] XIAO Liang, LIU Jinliang, LI Qiangda, et al. User-centric view of jamming games in cognitive radio networks[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(12): 2578–2590. doi: 10.1109/TIFS.2015.2467593 [2] AMURU S D and BUEHRER R M. Optimal jamming against digital modulation[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(10): 2212–2224. doi: 10.1109/TIFS.2015.2451081 [3] 王沙飞, 鲍雁飞, 李岩. 认知电子战体系结构与技术[J]. 中国科学: 信息科学, 2018, 48(12): 1603–1613. doi: 10.1360/N112018-00153WANG Shafei, BAO Yanfei, and LI Yan. The architecture and technology of cognitive electronic warfare[J]. Science in China:Information Sciences, 2018, 48(12): 1603–1613. doi: 10.1360/N112018-00153 [4] VINYALS O, BABUSCHKIN I, CZARNECKI W M, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning[J]. Nature, 2019, 575(7782): 350–354. doi: 10.1038/s41586-019-1724-z [5] QIAO Zhiqian, TYREE Z, MUDALIGE P, et al. Hierarchical reinforcement learning method for autonomous vehicle behavior planning[J]. arXiv preprint arXiv: 1911.03799, 2019. [6] BELLO I, PHAM H, LE Q V, et al. Neural combinatorial optimization with reinforcement learning[C]. The International Conference on Learning Representations, Toulon, France, 2017. [7] NAPARSTEK O and COHEN K. Deep multi-user reinforcement learning for distributed dynamic spectrum access[J]. IEEE Transactions on Wireless Communications, 2019, 18(1): 310–323. doi: 10.1109/TWC.2018.2879433 [8] AMURU S D, TEKIN C, VAN DER SCHAAR M, et al. Jamming bandits—A novel learning method for optimal jamming[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 2792–2808. doi: 10.1109/TWC.2015.2510643 [9] AMURU S and BUEHRER R M. Optimal jamming using delayed learning[C]. 2014 IEEE Military Communications Conference, Baltimore, USA, 2014: 1528–1533. [10] 颛孙少帅, 杨俊安, 刘辉, 等. 采用双层强化学习的干扰决策算法[J]. 西安交通大学学报, 2018, 52(2): 63–69. doi: 10.7652/xjtuxb201802010ZHUANSUN Shaoshuai, YANG Jun’an, LIU Hui, et al. An algorithm for jamming decision using dual reinforcement learning[J]. Journal of Xi'an Jiaotong University, 2018, 52(2): 63–69. doi: 10.7652/xjtuxb201802010 [11] 颛孙少帅, 杨俊安, 刘辉, 等. 基于正强化学习和正交分解的干扰策略选择算法[J]. 系统工程与电子技术, 2018, 40(3): 518–525. doi: 10.3969/j.issn.1001-506X.2018.03.05ZHUANSUN Shaoshuai, YANG Jun’an, LIU Hui, et al. Jamming strategy learning based on positive reinforcement learning and orthogonal decomposition[J]. Systems Engineering and Electronics, 2018, 40(3): 518–525. doi: 10.3969/j.issn.1001-506X.2018.03.05 [12] LI Yangyang, XU Yuhua, XU Yitao, et al. Dynamic spectrum anti-jamming in broadband communications: A hierarchical deep reinforcement learning approach[J]. IEEE Wireless Communications Letters, 2020, 9(10): 1616–1619. doi: 10.1109/LWC.2020.2999333 [13] KULKARNI T D, NARASIMHAN K R, SAEEDI A, et al. Hierarchical deep reinforcement learning: Integrating temporal abstraction and intrinsic motivation[C]. The 30th Conference on Neural Information Processing Systems, Barcelona, Spain, 2016: 3675–3683. [14] RAFATI J and NOELLE D C. Learning representations in model-free hierarchical reinforcement learning[C]. The AAAI Conference on Artificial Intelligence, Palo Alto, USA, 2019: 10009–10010. [15] FESTA P. A brief introduction to exact, approximation, and heuristic algorithms for solving hard combinatorial optimization problems[C]. 2014 16th International Conference on Transparent Optical Networks, Graz, Austria, 2014: 1–20. [16] GULCEHRE C, LE PAINE T, SHAHRIARI B, et al. Making efficient use of demonstrations to solve hard exploration problems[C]. The International Conference on Learning Representations, 2020. [17] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236 -





 下载:
下载:


 下载:
下载:
