Full-sea Depth Sound Speed Profiles Prediction Using RNN and Attention Mechanism
-
摘要: 海水中的声速剖面具有明显的时间演化特性，其预测问题可以看作一个非线性的时间序列预测问题。解决此类问题的常用方法大多使用预定义的非线性形式，无法捕捉真正潜在的非线性关系。循环神经网络作为一种为序列建模特别设计的深度神经网络，在捕捉非线性关系上具有极大的灵活性，在非线性自回归的时间序列预测这一问题上展现了它的有效性；注意力机制能够从众多信息中选择出对当前任务目标最关键的信息，对多变量时间序列在时空维度上的非线性关系进行捕捉。该文利用深度学习中的循环神经网络，添加双层注意力机制构建多变量时间序列预测模型，对浅海环境下时变的全海深声速剖面进行预测。多个模型的预测结果表明，该模型相对于单纯的编码-解码模型有着明显的预测性能提升，并且注意力权重的分布能够与实际物理现象相关联，为水声学中物理模型与机器学习的结合提供了新的思路。Abstract: The Sound Speed Profiles (SSPs) in sea water have obvious time evolution characteristics, and their prediction can be regarded as a nonlinear time series prediction. Recurrent Neural Networks (RNN), a type of deep neural network designed for sequence modeling, can capture nonlinear relationships flexibly. Attention Mechanism (AM), which selects the most critical information for the current task, can describe the nonlinear relationships in space and temporal dimensions. In this paper, RNN and AM are used to construct a multivariate time series prediction model to learn the historical SSPs and predict the time-varying full-sea SSPs in shallow sea environment. Experiments on real sound speed data show that the proposed method is effective and outperforms other methods, and provides a new idea for the combination of physical model and machine learning in underwater acoustics.
-
1. 引言
随着众多数字媒体设备的出现，同一张照片在不同显示设备上智能缩放，即图像缩放技术(image retargeting)已经得到了广泛的关注。图像缩放的主要目标是保证图像重要信息的同时改变图像的尺寸和分辨率，该方法已经在众多领域[1-4]得到了推广和应用。内容敏感缩放(context-aware method)作为非均匀缩放技术被广泛研究，其中包括Seam Carving[5]及其改进算法。
根据实现原理，内容敏感缩放模型可以分为两大类：(1)连续缩放模型，将图像映射为3维空间内的概率分布，根据显著性等因素修改映射程度达到图像缩放的目的，如warping算法[6,7]；(2)离散缩放模型，迭代寻找最小能量线(Seam)，通过增加或删除Seam实现图像缩放，如改进的Seam Carving(SC)算法[8,9]。本文主要关注离散缩放模型采用基于SC的内容敏感缩放算法。为了保证图像的重要区域不丢失，Zhou等人[10]提出的WSM模型(Wall-Seam Model)结合显著性特征和图像边缘信息，采用双向缩放保持图像重要信息的同时达到最小缩放扭曲。立体显著性[11]结合显著信息、景深信息和梯度能量信息，可以更加准确地估算每一个像素的重要性。文献[12,13]通过计算显著能量在物体边界的加速度不仅能够保持重要区域的结构信息，还能够对非显著区域的结构信息进行保护。然而，在上述方法中，缩放扭曲现象始终普遍存在，尤其是在物体边缘区域，这将会严重影响缩放图片的质量。主要原因有两方面：第一，在迭代式缩放过程中扭曲信息是递增出现的，等到出现严重的视觉缺陷时，扭曲现象已经过n(n>2)代叠加了；第二，Seam Carving算法的离散式缩放模式导致无法将缩放信息传递给下一代，无法在后续迭代中有效避免严重扭曲叠加现象。
为解决上述问题，本文提出新的SC连续模型，在每一次迭代后，Seam的移除 (增加)会导致轻微的像素位移。相邻像素间不同方向的位移累积会导致多次迭代后的潜在扭曲。本文提出最小位移可视差(Just Noticeable Distortion, JND)检测算法计算每次迭代中的像素位移。通过本文提出的能量权重(Energy Weight, Ew)，将JND信息传递到下一次迭代中，从而有效避免扭曲现象。Ew和JND的提出，使得改进SC算法从离散缩放模型变成连续缩放模型。通过与最新缩放算法在公共图像缩放数据集RetargetMe[14]进行对比实验，验证了本文方法的有效性和先进性。
2. 相关工作
SC算法采用8连通相邻最小能量线的方式，从上至下或从左至右对图像进行缩放。由于其算法的普适性和有效性吸引了大量研究人员的关注，基于改进SC的算法陆续出现。根据近年来的研究成果，改进算法大致可以分为3个方向。
第一，研究人员致力于图像显著性特征的改进，常用的显著性特征模型包括GBVS(Graph-Based Visual Saliency)模型[15]、Itti模型[16]和HSaliency模型[17]等。结合深度信息的立体显著性特征[11]、边缘特征[12,13]、阴影特征[8]和Global Scalar梯度特征[18]等不同特征可以辅助显著性特征，增强缩放后的重要信息保持。虽然多特征融合有助于更全面地捕捉图像信息，对于尽可能多地保持图像重要信息具有积极作用，但是这些特征中缺少对于图像内容和语义方面的指导，往往会导致缩放效果无法兼顾图像内容的语义完整性(边界扭曲)。
第二，多方法融合算法解决针对单一缩放模型的局限性。Fang等人[19]和Wei等人[20]分别在2017年和2018年提出融合Crop, SC, Warping, Scale和Stretch算法的图像缩放模型，能够获得普遍优于单一方法的效果。但是，针对不同类型图像如何调整和确定各方法间的平衡参数，以及昂贵的时间代价都对该方向算法的改进提出了挑战。
第三，还有研究学者采用其他的技术辅助SC算法，例如遗传算法[10]，Block Artifact Grid[21]和共形映射[22]等。辅助方法都能够针对某类图像获得较好的缩放效果，但是仍不能解决缩放扭曲的问题。本文研究在现有的3个改进方向的基础上提出了新的思路，即通过JND算法的提出将SC的离散缩放模型改进为连续模型，能够将每次迭代的缩放扭曲信息累加传递下去，从而改进缩放效果且抑制图像边缘扭曲现象。
3. 最小位移可视差检测算法
本文的主要研究目标是改进SC模型的图像缩放质量，减少缩放后的边缘扭曲现象。尽管现在已经存在很多改进算法且缩放质量逐步提高，经过反复试验发现对于大比例缩放和图像内容复杂的情况扭曲现象仍普遍存在。本文通过分析发现，该问题出现的主要原因在于SC算法的离散式迭代和最小能量函数法。最小能量函数法仅计算当前状态下的能量线(Seam)，离散式迭代导致前一次迭代信息无法传递到后续的缩放过程中。换句话说，如果第i次迭代出现了微小的扭曲，在离散式SC运行机制下扭曲位置无法在第i+1次迭代过程中得到保护。这将会导致接下来的k次迭代后，会出现扭曲放大进而影响缩放的美观性。因此本文提出假设：如果在每一次迭代过程中的最小扭曲可视差JND能够进行检测，并将其传递至随后的迭代过程中，则能有效降低扭曲出现的概率，提高缩放结果的质量。本文连续模型如图1所示，其中图(a)为离散SC模型，图(b)为本文提出的连续SC模型，通过结合JND信息和能量权重Ew·(SC+Ew)，图像缩放能量能够以累加的方式传递到后续的迭代过程中，有效抑制扭曲现象的出现。
3.1 位移可视差函数
方向相反的微小像素移动会产生微小的图像扭曲。经实验表明2个像素以内的位移不会产生可视化扭曲。在光流估计研究领域，相邻两帧的像素移动可以通过最小化位移差进行计算[23]。受此启发，本文定义最小位移可视差JND为像素位移向量，
u= (u,v)T ，其中u表示水平位移，v表示垂直位移。JND信息可以通过计算相邻两次迭代Seam Carving结果的能量相似性进行表达。本文希望在保持图像重要信息的前提下，相邻两次迭代Seam Carving结果具有最高的相似性。也就是说，目标函数可以表示为Seam Carving的能量差最小化问题，如式(1)所示。ED(u)=∑x12||I2(x+u)−I1(x)||+12α||∇I2(x+u)−∇I1(x)|| (1) 其中，α表示权重，
I1 为Seam Carving之前的图像，I2 为Seam Carving之后的图像，x为图像中的像素，∇ 为梯度计算。式(1)的第1项为颜色不变约束，第2项为梯度约束。如果u计算准确，则ED(u) 将趋向于0。根据参考文献[23]，一个好的模型应该倾向于含有更多信息的约束，而不是所有约束。我们定义一个二分权重映射θ(γ):Z2→{0,1} ，在优化过程中通过遍历决定采用哪一项约束。新的能量函数可以表示为ED(u)=∑xθ(γ)||I2(x+u)−I1(x)||+(1−θ(γ))α||⋅∇I2(x+u)−∇I1(x)|| (2) 当
θ(γ)=0 时，梯度约束起作用；当θ(γ)=1 时，颜色不变约束起作用。在Seam Carving过程中，物体边界对于缩放后的效果起重要的影响。因此，我们定义边界保持正则项对位移能量进行约束，如式(3)。
Es(u)=∑xω(x)||∇(u)(x)|| (3) 其中，
x∈Z2 ，并且||∇(u)(x)|| 为TV正则项，ω(x) 为简单结构适应映射[23]。因此，最终的可视化能量函数可以定义为式(4)E(u,θ)=ED(u)+λEs(u) (4) 其中，λ为正则项权重。
3.2 近似最小化寻优
当位移可视差u计算最准确时，式(4)能够取得最小值。因此，计算u的过程可以看作对式(4)的最小化寻优过程，最终目标函数可以表示为式(5)：
F=minu,θE(u,θ) (5) 最小化过程中需要同时对两个变量u和θ进行计算，一般采用迭代优化策略。在本文问题中，θ是二分映射，因此我们可以用平均场近似算法[24](Mean Field approximation, MF)化简优化。通过特定状态替换θ减少一个变量简化寻优过程。特定状态的当前系统概率分布可以表示为式(6)：
P(u,θ)=1Ze−βE(u,θ) (6) 其中，β表示温度反转的阈值，Z表示状态划分函数。Z可以表示为式(7)：
Z=∑u∑θe−βE(u,θ) (7) 沿鞍点方向所有的θ状态代入式(7)可近似得到
Z=∑{u}∑{θ=0,1}e−βE(u,θ)=∑{u}e−βEs(u)⋅∑{θ=0,1}e−β∑x(θ(x)ΨI(u,x)+(1−θ(x))Ψ∇I(u,x))=∑{u}e−βEs(u)∏x(e−βΨI(u,x)+e−βΨ∇I(u,x))=∑{u}e−β{Es(u)−∑x1β(ln(e−βΨI(u,x)+e−βΨ∇I(u,x)))}≈maxue−β{Es(u)−∑x1β(ln(e−βΨI(u,x)+e−βΨ∇I(u,x)))} (8) 其中，
ΨI(u,x)=I2(x+u)−I1(x) 和Ψ∇I(u,x)= ∇I2(x+u)−∇I1(x) 。因此对式(5)的最小化可以近似为对式(8)的最小化。在式(8)中只有一个变量, 将会降低优化难度。本文提出有效位移可视差函数可以表示为EeffD(u)=λEs(u)−∑x1βln(e−βΨI(u,x)+e−βΨ∇I(u,x)) (9) 将式(9)代入式(5)，最终最小化目标函数可以表示为
F=minuEeffD(u) (10) 通过对单变量u进行寻优，可以计算出每一次Seam Carving迭代后的最小位移可视差作为JND信息。
4. 连续Seam Carving模型
最小位移可视差检测算法可以获得每次迭代后缩放的JND信息。在此基础上，为了解决传统离散模型对于缩放信息无法传递的问题，本文提出采用能量权重Ew表示累加缩放信息。JND中基于8连通域的相邻像素移动方向相反表明该处大概率会出现扭曲现象。将该位置信息通过权重增加的方式记录在Ew中，并在后续的最小能量线查找过程中进行适当的保护可以降低扭曲现象出现的概率。本文算法处理流程如图2所示。每一次迭代过程中，首先对目标图像提取特征，然后通过SC算法，结合上一次迭代的Ew寻找最小能量线进行缩放；然后将缩放前和缩放后的图像计算JND信息，将扭曲像素位置在Ew中进行叠加传递到下一次迭代过程中，从而将离散的SC模型变为连续模型。
引入JND信息和Ew后的Seam Carving缩放过程可以表示为式(11)—式(13)：
fen=Esa+Ede+Eed+Egr (11) Eiw=i∑i−k+1JNDi−1,i∈[1,n],k∈[1,i] (12) Ire(x,y)=minx,y∈I(Eiw⋅fen) (13) 根据文献[12,13]，本文将显著特征
Esa 、景深特征Ede 、边缘特征Eed 和梯度特征Egr 相结合进行最小能量线搜索。每一次迭代的能量权重是通过前k代的JND信息叠加产生的，如式(12)，其中JND0={0,0,···} 即第1次迭代时默认最小位移可视差为0。能量权重Ew可以叠加前k代的位移差对当前最小能量线搜索进行约束，通过式(13)可以计算出最小能量线。便于计算本文在实验中设置k=1，n为缩放指定的迭代次数。连续Seam Carving图像缩放算法如表1所示。
表 1 连续Seam Carving图像缩放算法输入：目标图像, Iin，缩放比例参数, n 输出：缩放结果图像，Iout 1: repeat 2: 根据式(11)计算fen 3: 根据式(12)计算Eiw 4: 微小缩放I2和I1至相同大小 5: 根据式(9)和式(10)计算ui 6: 进行缝合计算 7: 更新缩放参数 8: until seamnum=n 5. 实验结果分析
5.1 实验设置
本文实验环境为i7-6700 3.4 GHz, 16 GB DDR内存，GTX1070显卡，显存8 GB, MATLAB R2015b。本文使用3个特征：显著性特征Hsaliency[17]，景深特征JNB[25]和结构保持性边界信息[13]。实现过程中的相关参数为：式(9)中的λ=0.5, β=5。
本文主要实验数据来自图像缩放公共数据集RegargetMe。为了验证算法的有效性共设计并实现3组实验：第1组实验与当前Seam Carving改进算法进行对比，包括SC[5], WSM[10], SC+SA+DE[11]和本文算法，验证本文方法针对SC模型改进的有效性；第2组实验与当前最新其他方法进行比较，验证本文算法在图像缩放方面的先进性，包括Crop, SC, Warping[6], SNS[26]，本文方法离散模型和本文方法连续模型；第3组为定量对比，分别采用当前主流图像缩放质量评估算法Sift-flow[27], ARS[28,29]和Vssm[30]进行定量对比。
5.2 定性实验对比和分析
在第1组实验中，我们针对其他Seam Carving改进算法进行对比实验。针对高分辨率图像和运动图像进行大比例缩放实验(缩放比例超过60%)，见图3。
在图3中，儿童草地图为高清图像，SC算法和SA+DE+SC算法都造成了小孩身体的缩小或头部扭曲，WSM算法删除了远处的彩带，本文算法在前景和背景保持方面都表现良好。在赛车图中，SC算法导致赛车严重缩小，WSM算法造成赛道扭曲，SA+DE+SC算法和本文算法表现良好。在滑板图中，SC算法和SA+DE+SC算法都对人物及其影子产生了严重的扭曲，WSM算法对于背景街道有所扭曲，本文算法对于运动图像，无论前景还是背景都保持最为完整。通过第1组实验可以证明本文方法对于扭曲现象具有明显的减少效果。为了更好地体现JND算法在抑制扭曲方面的效果，我们在图3所示的缩放过程中，计算前500次迭代过程中的像素级平均扭曲度(JND errors)，将其归一化至[0, 1]区间内，如图4所示。图像扭曲度在缩放开始阶段都比较小，随着缩放迭代数的增加，扭曲度都在不同程度的递增(0–150代)。其中，SC算法由于只考虑到图像梯度能量，扭曲产生得最快；WSM算法增加了边缘信息的检测，扭曲度的增加比SC算法略缓。SA+DE+SC算法通过景深能量值和显著性能量值的约束，扭曲度的增加相较于SC算法和WSM算法更加缓慢。与此3种算法不同的是，本文算法能够及时地检测扭曲度并且通过Ew传递到下一代，因此本文算法的扭曲度虽然在初期也随着迭代逐步递增，但到达一定程度后(0.45)扭曲度递增程度逐渐降低，并能保持在相对较低的范围内。由此可以证明本文提出的连续SC模型能够对扭曲进行抑制，有效地避免了大规模的扭曲现象。
第2组实验中，本文与当前主流的各种算法进行了对比，包括传统缩放方法Crop，经典离散缩放方法SC, SNS(Scale-and-Stretch)，经典连续缩放方法Warping, JND+离散SC和JND+连续SC。实验数据全部来自RegargetMe，选取其中4类图像：人物、建筑、自然风光和动植物进行多次实验，如图5。
在图5中，从左到右依次为：(a)原图，(b)Crop算法，(c)标准Seam Carving算法，(d)SNS算法，(e)Warping算法，(f)JND+离散SC模型，(g)JND+连续SC模型。其中，Crop算法能够最完美地保持图像中的重要区域(包括细节与尺寸)，但是会造成图像两侧数据的大量丢失；SC算法在人脸、建筑都产生了扭曲；SNS算法虽然扭曲比较少，但是图像中的重要信息尺寸缩减得最严重，例如蝴蝶；Warping算法在自然风景和动植物图像中都产生了重要信息没有完整保存的问题。JND+离散SC算法中，人物的脸部明显扭曲，建筑图像的尺寸缩减较大。相比较前面的算法，JND+连续SC算法在4类图像方面都取得了非常好的缩放效果，在重要信息保持、抑制扭曲现象方面综合来看明显优于前面的算法。
5.3 定量实验对比和分析
当前，对于图像缩放算法主流的评价方法还是基于用户的视觉判断。近年来陆续出现针对缩放质量评估的算法，本文选用其中的3个：Sift-flow, ARS, Vssm。其中，Sift-flow算法能够计算原始图像与缩放图像之间的稠密相关性，用来衡量图像缩放后内容的保持程度，结果越高越好。ARS算法为近年来提出的，通过计算局部block的变化有效地评价缩放后的图像扭曲程度，结果越高越好。Vssm算法通过双向patch比较评估显著性区域的不相似程度，结果越低越好。
本文在上述4个图像类别中，每类图像选取5幅，其中人物图像和建筑图像采用50%的缩放比，自然景观图像和动植物图像采用60%的缩放比率。通过计算缩放前后图像在3个评价算法的平均得分进行对比，具体如表2所示，DISJND表示JND+离散SC模型，CONJND表示JND+连续SC模型。
表 2 图像缩放定量对比Crop SC SNS WARP DISJND CONJND Sift-flow 0.37 0.57 0.69 0.38 0.59 0.79 ARS 0.94 0.89 0.90 0.89 0.89 0.91 Vssm 0.25 0.68 0.68 0.75 0.65 0.42 表2中数据显示了本文方法在4个图像类别中的图像缩放优越性。对于Sift-flow算法评价越高意味着缩放后的图像与原图像联系越大。通过对比发现，本文算法提出的JND+连续SC模型在该指标评价高达0.79。对于ARS算法，Crop方法获得最高的评价指标，这是因为Crop能够原样保存图像缩放前的重要区域，不会产生扭曲。但是会造成图像背景信息的大量丢失。除了Crop算法，本文算法在扭曲约束方面表现最好。对于Vssm算法，同样是Crop方法获得最高的评价指标，这是因为基于剪裁的方法，图像重要区域与原图基本相同，因此不相似性最低。除去Crop算法，本文算法仍旧获得最佳评价。通过定量对比实验得出的结论基本与5.2节的定性对比实验结果一致。
6. 结束语
本文提出最小位移可视差检测算法，能够在SC每次迭代过程中计算会造成扭曲的JND信息，通过本文提出的能量权值逐代累加传递下去，有效地将离散的SC模型变为连续模型，从而降低了传统SC过程中出现的扭曲现象。通过实验证明，基于JND的SC连续模型对于当前图像缩放算法在性能上带来较大的提高。
但由于加大了每次迭代的计算量，本文方法存在耗时严重的问题。采用GPU并行算法或其他加速算法减少时间复杂度将是未来需要解决的问题之一。另外，为了进一步提高图像缩放质量，改进的SC模型与其他算法的结合将会是未来的潜在研究方向。
-
表 1 不同模型对全海深声速剖面的预测性能
模型 数据集1 数据集2 数据集3 数据集4 ˉE Ebest ˉE Ebest ˉE Ebest ˉE Ebest Encoder-Decoder (32) 0.3319 0.2370 0.5521 0.3818 0.3802 0.2264 0.2831 0.1763 Encoder-Decoder (64) 0.2899 0.2224 0.4395 0.3144 0.2590 0.2109 0.2225 0.1744 Encoder-Decoder (128) 0.2332 0.1802 0.3360 0.2631 0.2438 0.1362 0.1702 0.0925 Encoder-Decoder (256) 0.1953 0.1604 0.2732 0.1678 0.1593 0.0923 0.1399 0.0885 Encoder-Attn-LSTM (32) 0.2467 0.1308 0.3564 0.2232 0.2178 0.1028 0.1375 0.0987 Encoder-Attn-LSTM (64) 0.2263 0.1210 0.3128 0.2216 0.1884 0.1132 0.1197 0.0842 Encoder-Attn-LSTM (128) 0.2001 0.1201 0.2835 0.1881 0.1525 0.0956 0.1055 0.0691 Encoder-Attn-LSTM (256) 0.1776 0.0931 0.2595 0.2022 0.0942 0.0563 0.0919 0.0541 Decoder-Attn-LSTM (32) 0.2245 0.1672 0.3769 0.2592 0.2103 0.1076 0.1293 0.0976 Decoder-Attn-LSTM (64) 0.2091 0.1635 0.3384 0.2150 0.1879 0.1101 0.1172 0.0807 Decoder-Attn-LSTM (128) 0.2061 0.1250 0.3129 0.2427 0.1508 0.0939 0.1029 0.0667 Decoder-Attn-LSTM (256) 0.1591 0.1111 0.2658 0.1628 0.1023 0.0597 0.0911 0.0620 DA-LSTM(32) 0.1072 0.0515 0.1794 0.1005 0.1287 0.0711 0.1245 0.1010 DA-LSTM (64) 0.0975 0.0456 0.1477 0.0948 0.1068 0.0512 0.1019 0.0532 DA-LSTM (128) 0.0802 0.0428 0.1264 0.0878 0.0806 0.0459 0.0893 0.0708 DA-LSTM (256) 0.0609 0.0312 0.1116 0.0811 0.0604 0.0341 0.0768 0.0414 
下载: 导出CSV
-
[1] 李启虎. 水声学研究进展[J]. 声学学报, 2001, 26(4): 295–301. doi: 10.3321/j.issn:0371-0025.2001.04.002LI Qihu. Advances of research work in underwater acoustics[J]. Acta Acustica, 2001, 26(4): 295–301. doi: 10.3321/j.issn:0371-0025.2001.04.002 [2] 汪德昭, 尚尔昌. 水声学[M]. 2版. 北京: 科学出版社, 2013: 9. [3] 张建华. 海温预报知识讲座 第一讲 海水温度预报概况[J]. 海洋预报, 2003, 20(4): 81–85. doi: 10.3969/j.issn.1003-0239.2003.04.013ZHANG Jianhua. Lectures on sea surface temperature prediction[J]. Marine Forecasts, 2003, 20(4): 81–85. doi: 10.3969/j.issn.1003-0239.2003.04.013 [4] KURAPOV A L, EGBERT G D, MILLER R N, et al. Data assimilation in a Baroclinic coastal ocean model: Ensemble statistics and comparison of methods[J]. Monthly Weather Review, 2002, 130(4): 1009–1025. doi: 10.1175/1520-0493(2002)130<1009:DAIABC>2.0.CO;2 [5] MUNK W, WORCESTER P, and CWUNSCH C. Ocean Acoustic Tomography[M]. Cambridge: Cambridge University Press, 1995. [6] LEBLANC L R and MIDDLETON F H. An underwater acoustic sound velocity data model[J]. The Journal of the Acoustical Society of America, 1980, 67(6): 2055–2062. doi: 10.1121/1.384448 [7] DAUGHERTY J R and LYNCH J F. Surface wave, internal wave, and source motion effects on matched field processing in a shallow water waveguide[J]. The Journal of the Acoustical Society of America, 1990, 87(6): 2503–2526. doi: 10.1121/1.399098 [8] TOLSTOY A, DIACHOK O, and FRAZER L N. Acoustic tomography via matched field processing[J]. The Journal of the Acoustical Society of America, 1991, 89(3): 1119–1127. doi: 10.1121/1.400647 [9] ZHU Guolei, WANG Yingmin, and WANG Qi. Matched field processing based on Bayesian estimation[J]. Sensors, 2020, 20(5): 1374. doi: 10.3390/s20051374 [10] SHEN Yining, PAN Xiang, ZHENG Zheng, et al. Matched-field geoacoustic inversion based on radial basis function neural network[J]. The Journal of the Acoustical Society of America, 2020, 148(5): 3279–3290. doi: 10.1121/10.0002656 [11] 崔宝龙, 徐国军, 笪良龙, 等. 采用小生境遗传算法反演浅海声速剖面研究[J]. 应用声学, 2021, 40(2): 279–286. doi: 10.11684/j.issn.1000-310X.2021.02.016CUI Baolong, XU Guojun, DA Lianglong, et al. Shallow sea sound speed profile inversion based on niche genetic algorithm[J]. Applied Acoustics, 2021, 40(2): 279–286. doi: 10.11684/j.issn.1000-310X.2021.02.016 [12] TAROUDAKIS M I and PAPADAKIS J S. A modal inversion scheme for ocean acoustic tomography[J]. Journal of Computational Acoustics, 1993, 1(4): 395–421. doi: 10.1142/S0218396X93000214 [13] SKARSOULIS E K, ATHANASSOULIS G A, and SEND U. Ocean acoustic tomography based on peak arrivals[J]. The Journal of the Acoustical Society of America, 1996, 100(2): 797–813. doi: 10.1121/1.416212 [14] YARDIM C, GERSTOFT P, and HODGKISS W S. Tracking of geoacoustic parameters using Kalman and particle filters[J]. The Journal of the Acoustical Society of America, 2009, 125(2): 746–760. doi: 10.1121/1.3050280 [15] CARRIÈRE O, HERMAND J P, LE GAC J C, et al. Full-field tomography and Kalman tracking of the range-dependent sound speed field in a coastal water environment[J]. Journal of Marine Systems, 2009, 78 Suppl: S382-S392. [16] CARRIERE O, HERMAND J P, and CANDY J V. Inversion for time-evolving sound-speed field in a shallow ocean by ensemble Kalman filtering[J]. IEEE Journal of Oceanic Engineering, 2009, 34(4): 586–602. doi: 10.1109/JOE.2009.2033954 [17] 金丽玲, 李建龙, 徐文. 自回归状态空间模型下时变声速剖面跟踪方法[J]. 声学学报, 2016, 41(6): 813–819.JIN Liling, LI Jianlong, and XU Wen. Tracking of time-evolving sound speed profiles with the auto-regressive state-space model[J]. Acta Acustica, 2016, 41(6): 813–819. [18] 苏林, 任群言, 庞立臣, 等. 强非线性时间演化声速剖面的序贯反演[J]. 声学学报, 2019, 44(4): 452–462.SU Lin, REN Qunyan, PANG Lichen, et al. Sequential inversion of highly nonlinear time-evolving sound speed profiles[J]. Acta Acustica, 2019, 44(4): 452–462. [19] 庞立臣, 胡涛, 傅德龙, 等. 集合卡尔曼滤波在时变声速剖面追踪中的性能分析[J]. 声学学报, 2020, 45(2): 176–188.PANG Lichen, HU Tao, FU Delong, et al. Performances of the ensemble Kalman filter on the tracking of time-evolving sound speed profiles[J]. Acta Acustica, 2020, 45(2): 176–188. [20] LINS I D, DAS CHAGAS MOURA M, SILVA M A, et al. Sea surface temperature prediction via support vector machines combined with particle swarm optimization[C]. International Probabilistic Safety Assessment & Management Conference, Seattle, USA, 2010: 16–29. [21] TANGANG F T, HSIEH W W, and TANG B. Forecasting the equatorial Pacific sea surface temperatures by neural network models[J]. Climate Dynamics, 1997, 13(2): 135–147. doi: 10.1007/s003820050156 [22] NOWRUZI H and GHASSEMI H. Using artificial neural network to predict velocity of sound in liquid water as a function of ambient temperature, electrical and magnetic fields[J]. Journal of Ocean Engineering and Science, 2016, 1(3): 203–211. doi: 10.1016/j.joes.2016.07.001 [23] JAIN S and ALI M M. Estimation of sound speed profiles using artificial neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 467–470. doi: 10.1109/LGRS.2006.876221 [24] SUN Sijia and ZHAO Hangfang. Sparse representation of sound speed profiles based on dictionary learning[C]. 2020 13th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Chengdu, China, 2020: 484–488. [25] ZHANG Qin, WANG Hui, DONG Junyu, et al. Prediction of sea surface temperature using long short-term memory[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1745–1749. doi: 10.1109/LGRS.2017.2733548 [26] SARKAR P, JANARDHAN P, and ROY P. Applicability of a long short-term memory deep learning network in sea surface temperature predictions[C]. Earth 1st International Conference on Water Security and Sustainability, Rangpo, Indin, 2019. [27] SARKAR P P, JANARDHAN P, and ROY P. Prediction of sea surface temperatures using deep learning neural networks[J]. SN Applied Sciences, 2020, 2(8): 1458. doi: 10.1007/s42452-020-03239-3 [28] QIN Yao, SONG Dongjin, CHENG Haifeng, et al. A dual-stage attention-based recurrent neural network for time series prediction[C]. Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 2017: 2627–2633. [29] HUANG Siteng, WANG Donglin, WU Xuehan, et al. DSANet: Dual self-attention network for multivariate time series forecasting[C]. Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 2019: 2129–2132. [30] MNIH V, HEESS N, GRAVES A, et al. Recurrent models of visual attention[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2204–2212. -
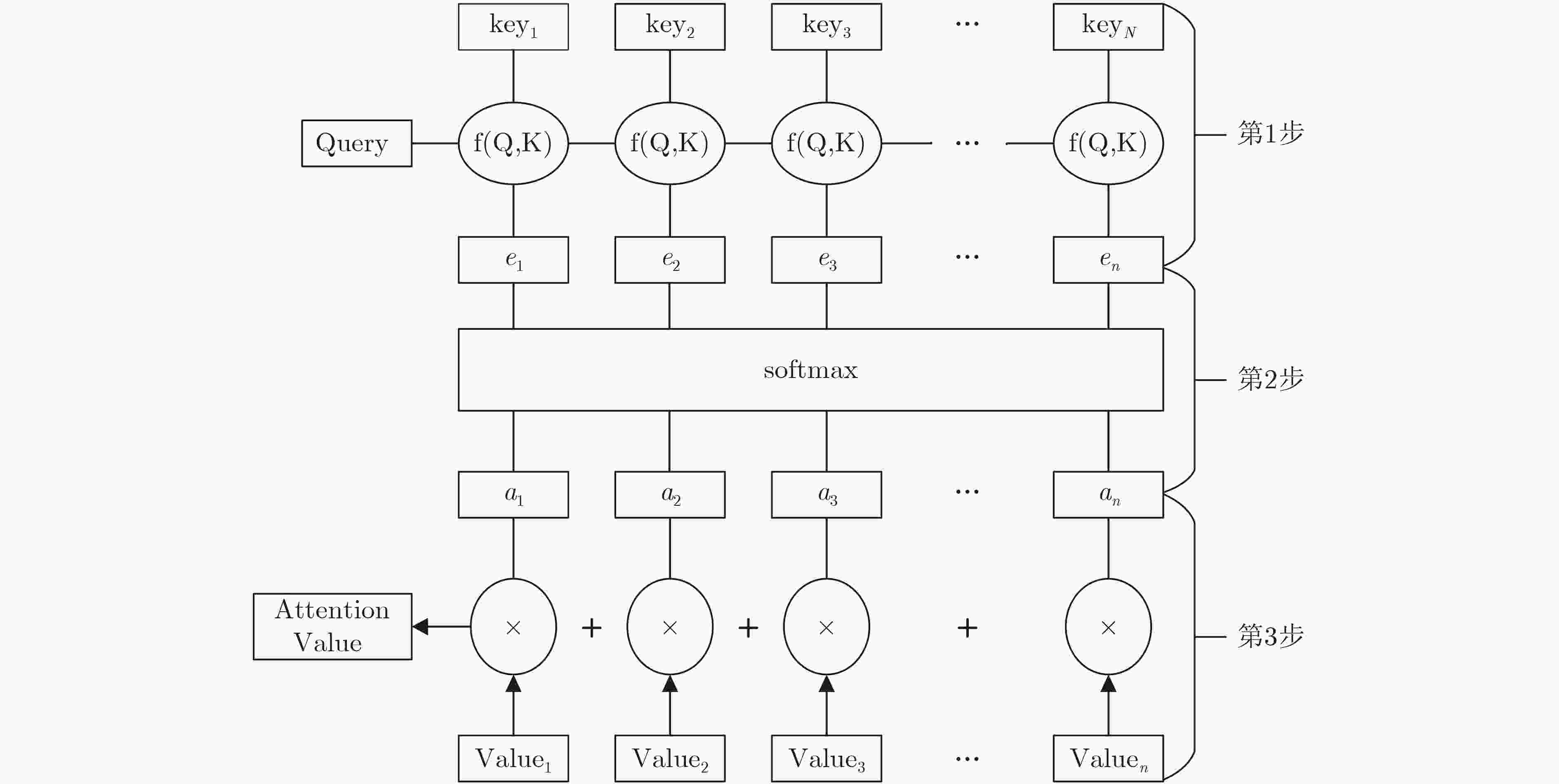
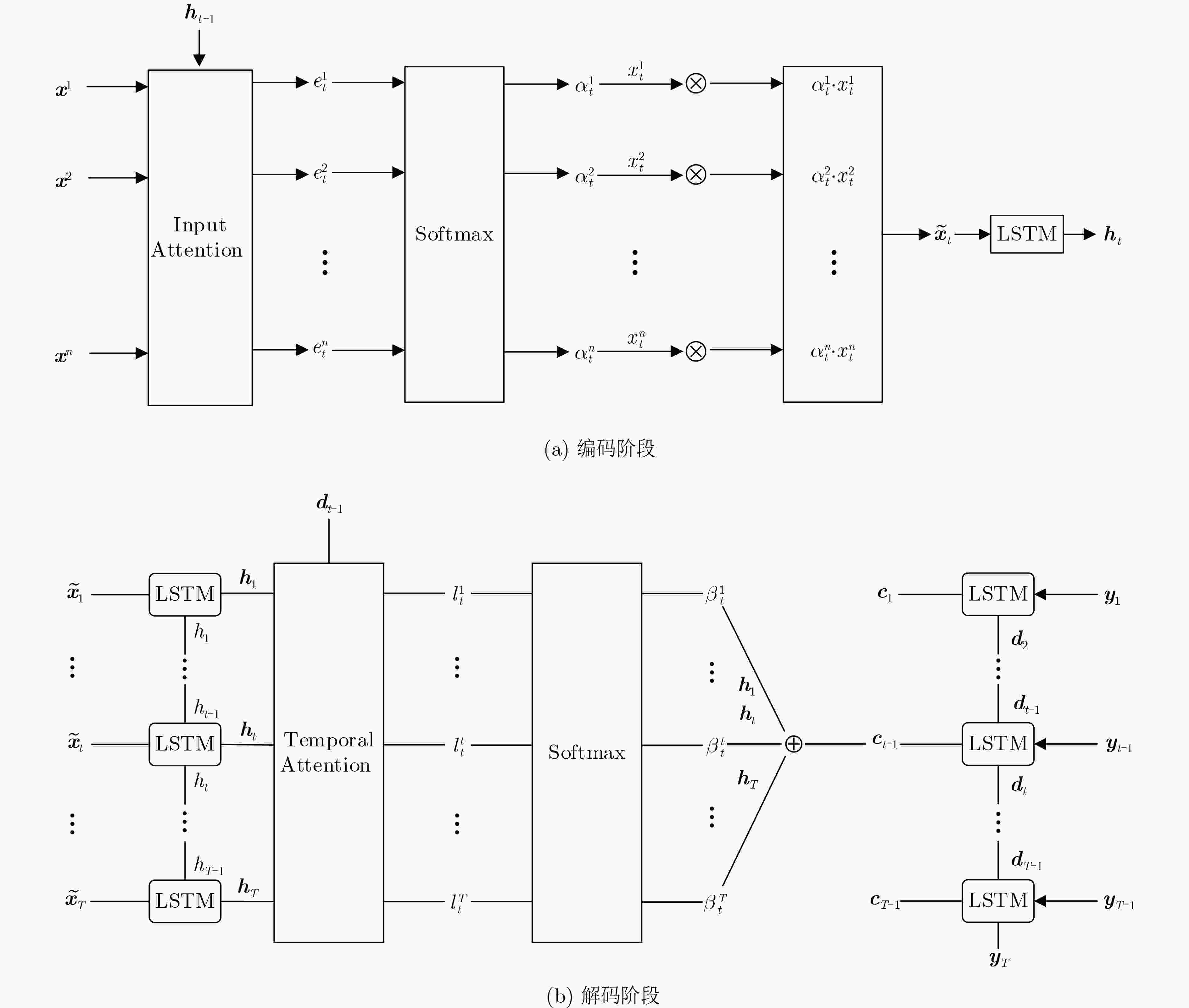
下载:
计量
- 文章访问数: 1129
- HTML全文浏览量: 575
- PDF下载量: 139
- 被引次数: 0
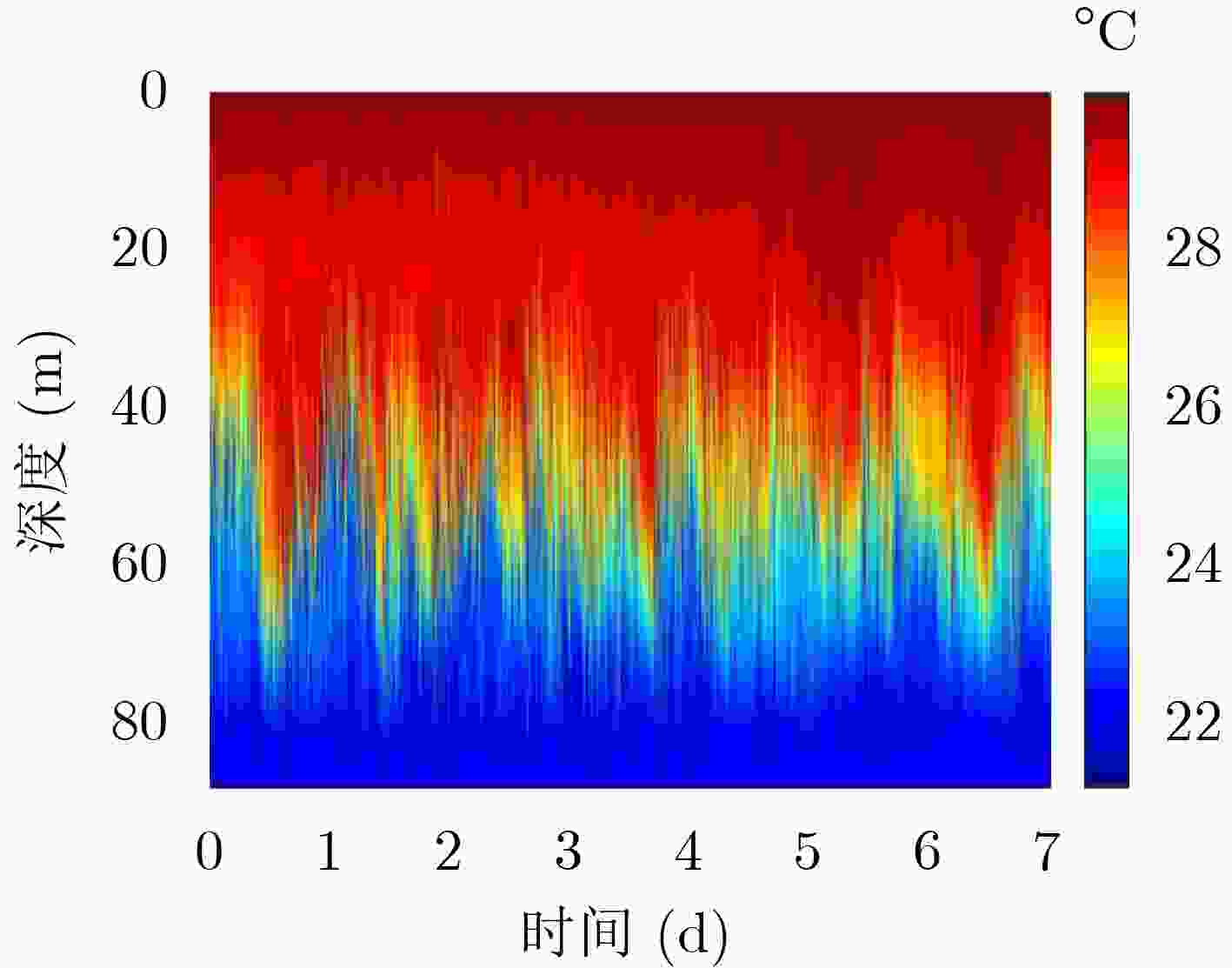
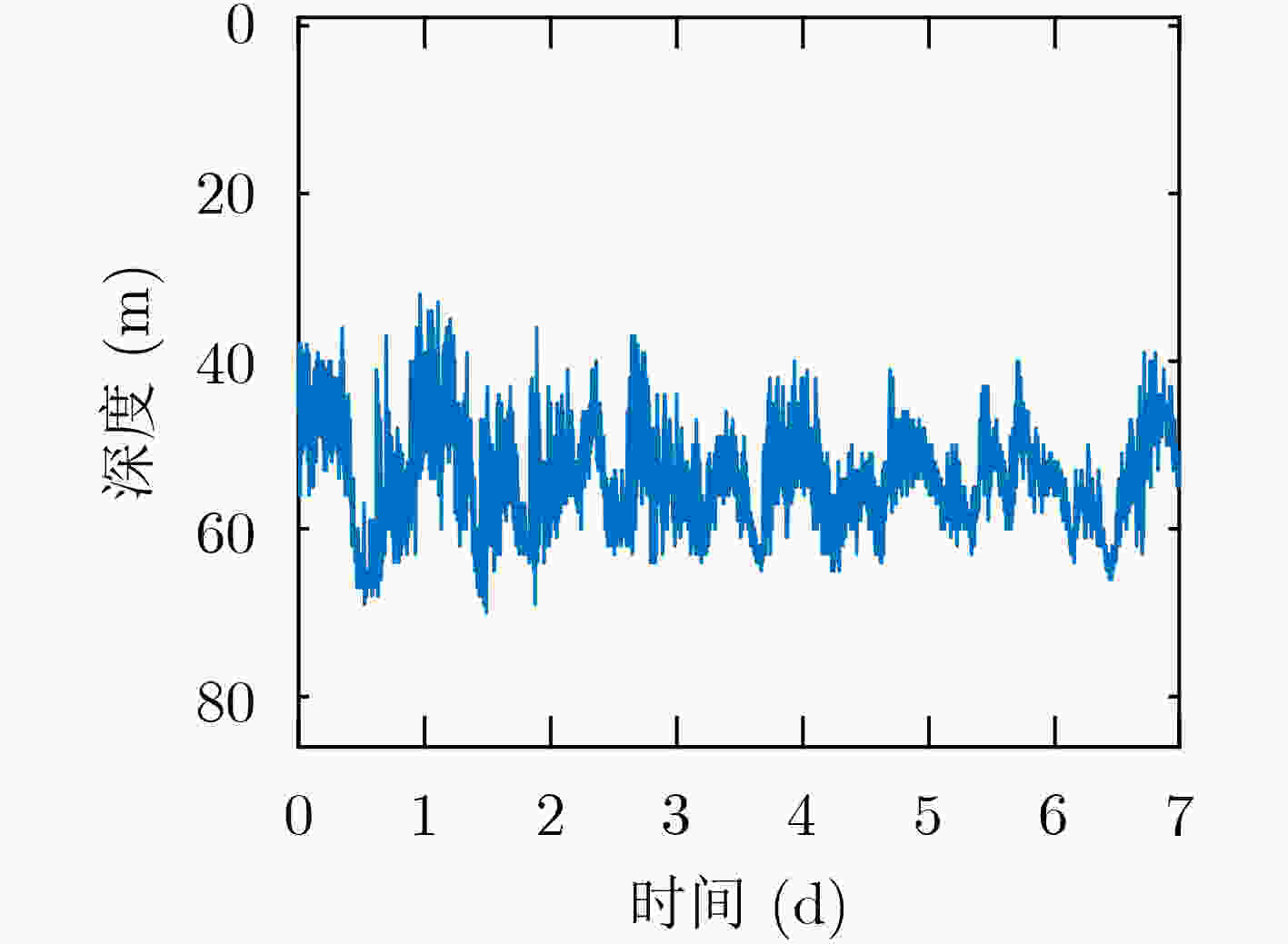
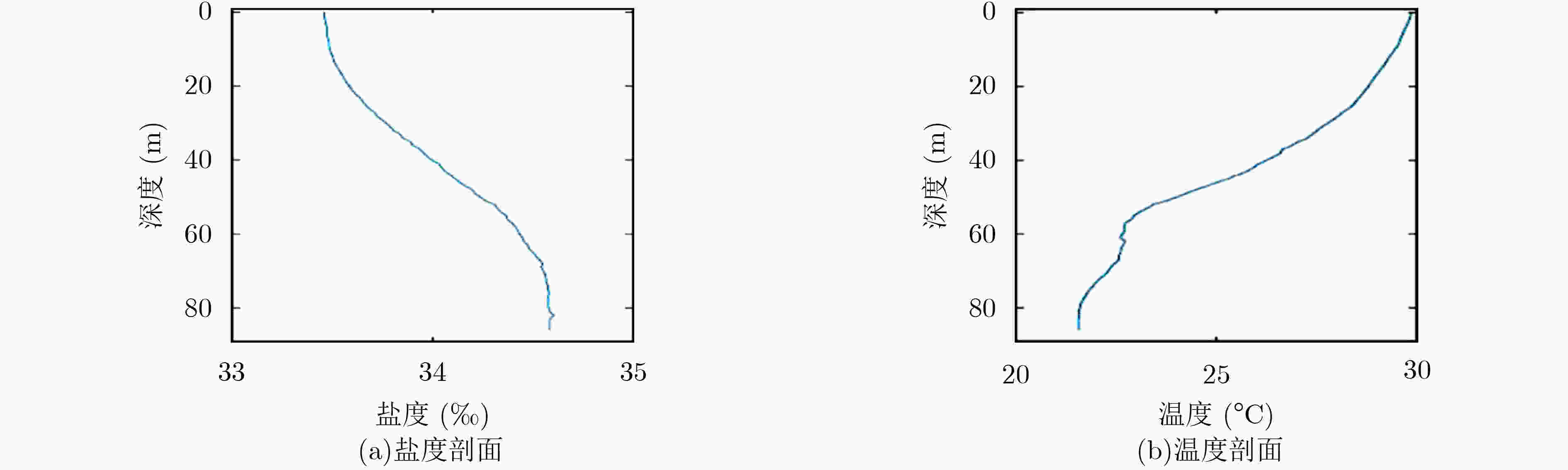
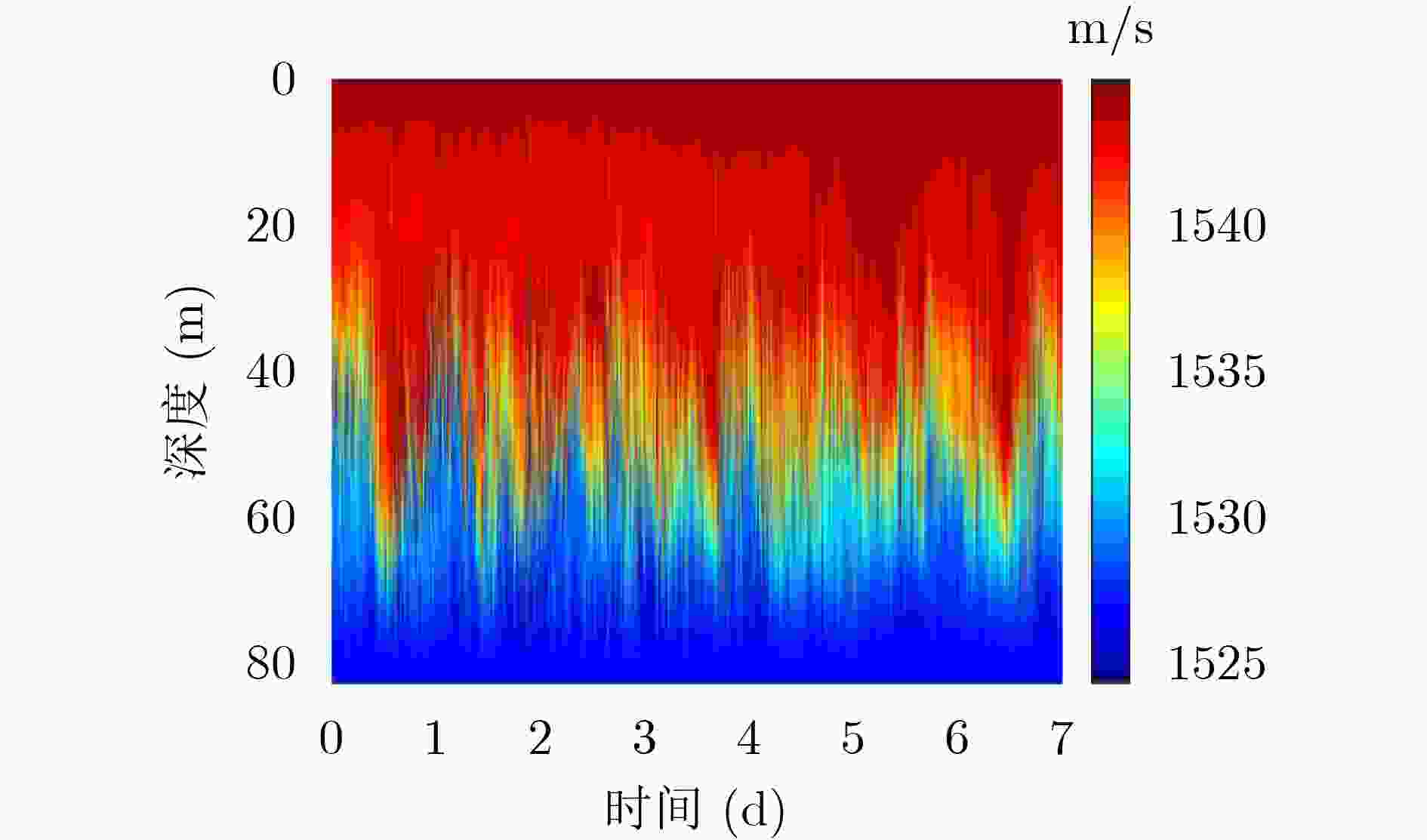
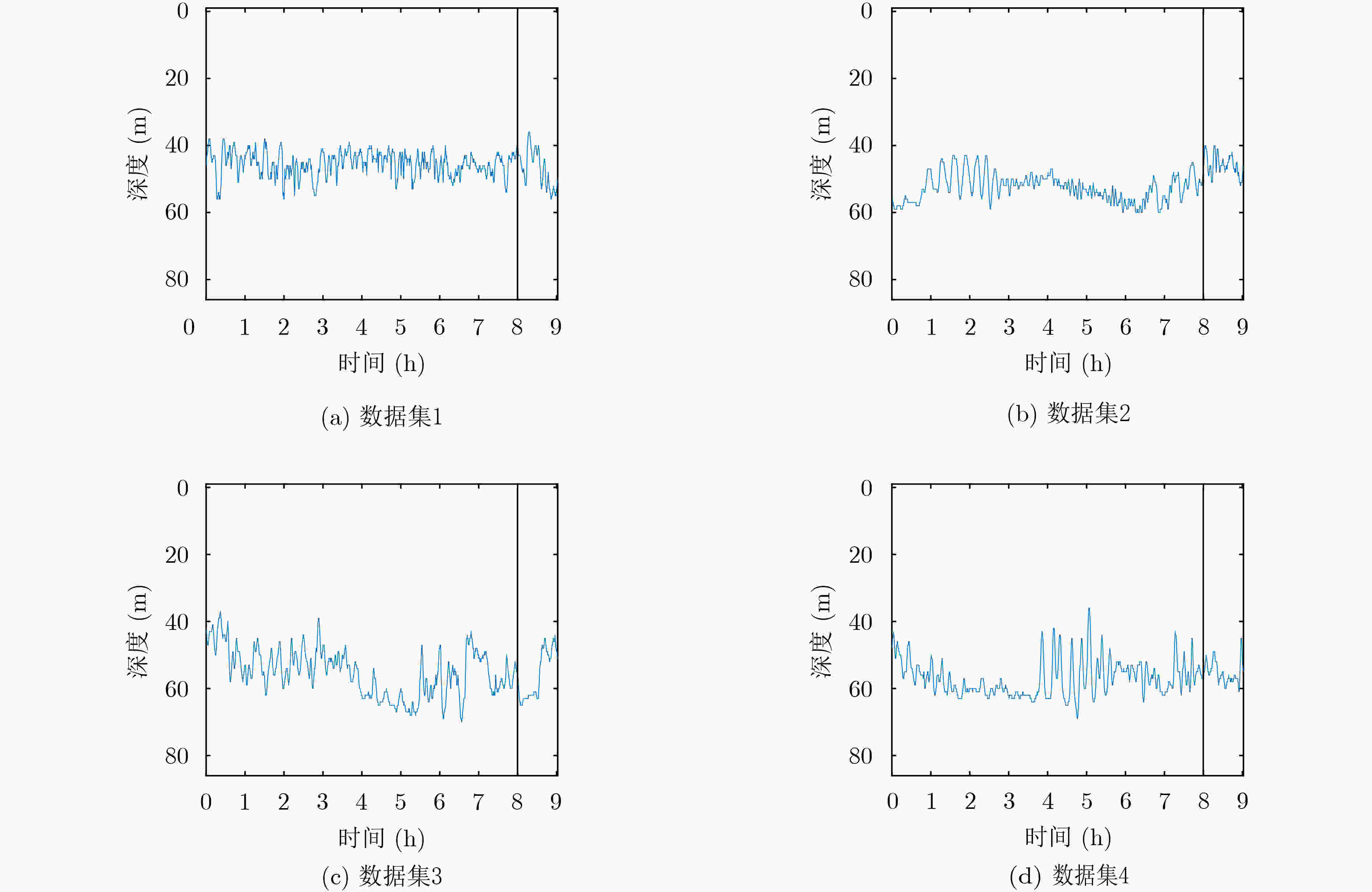
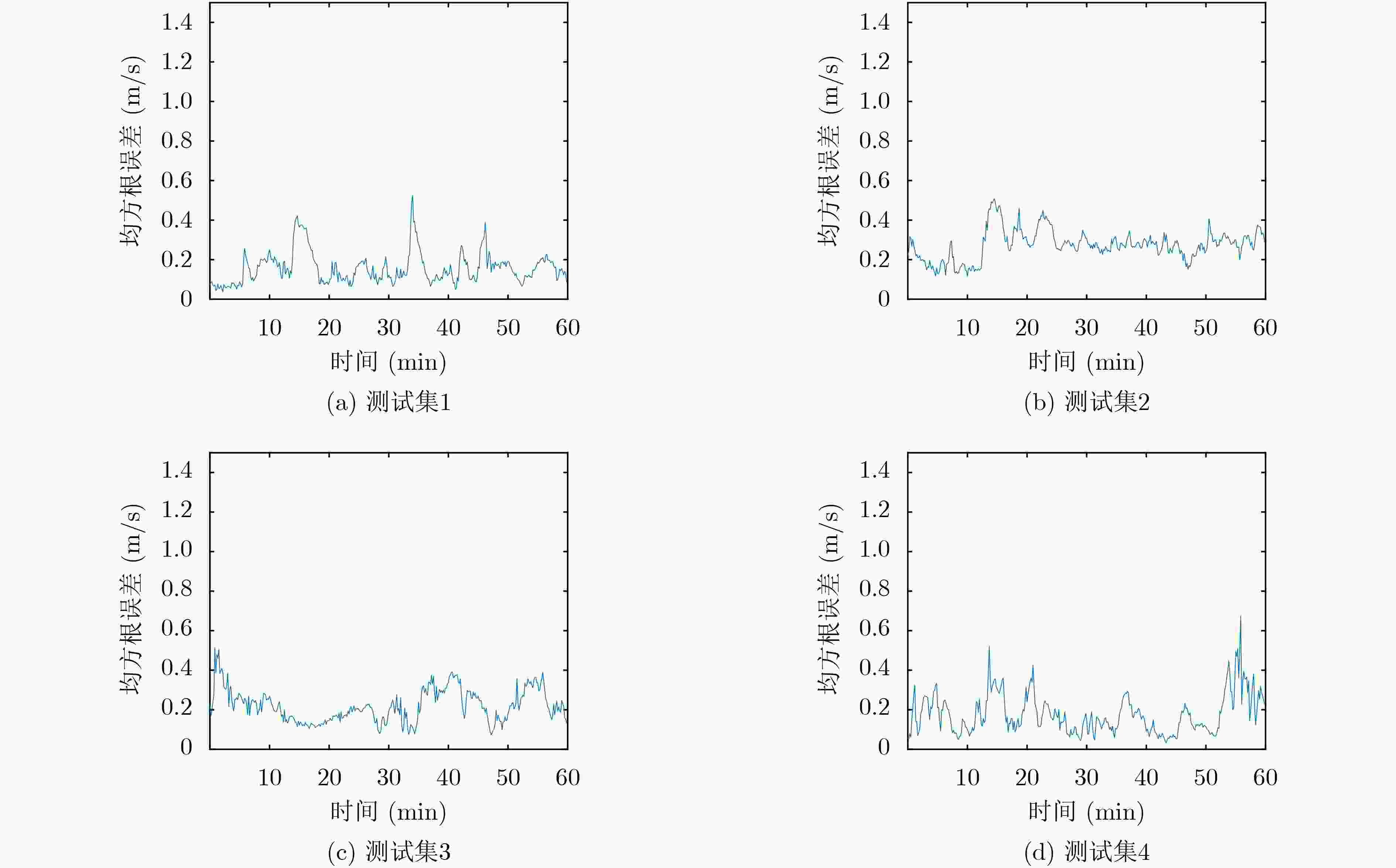
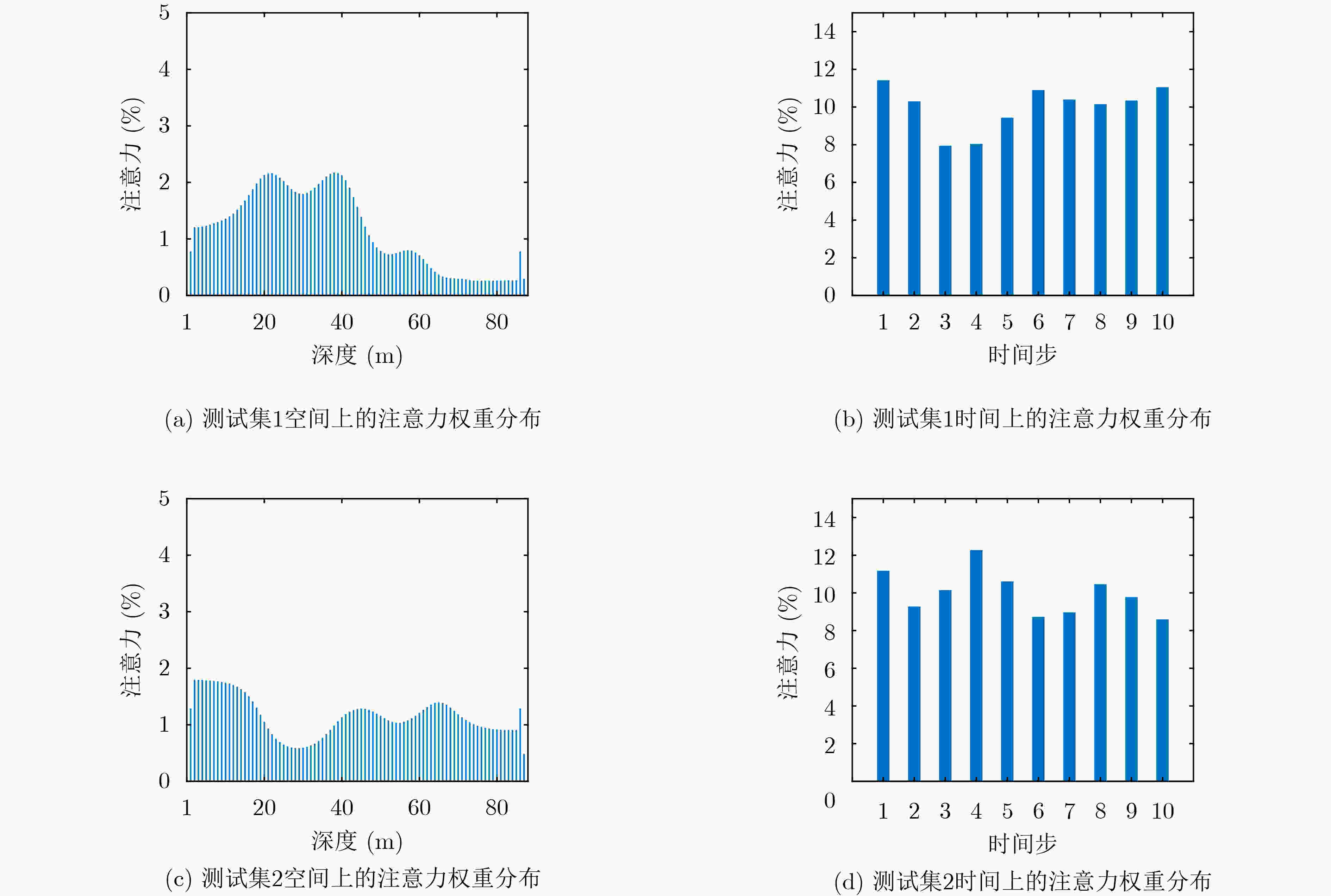
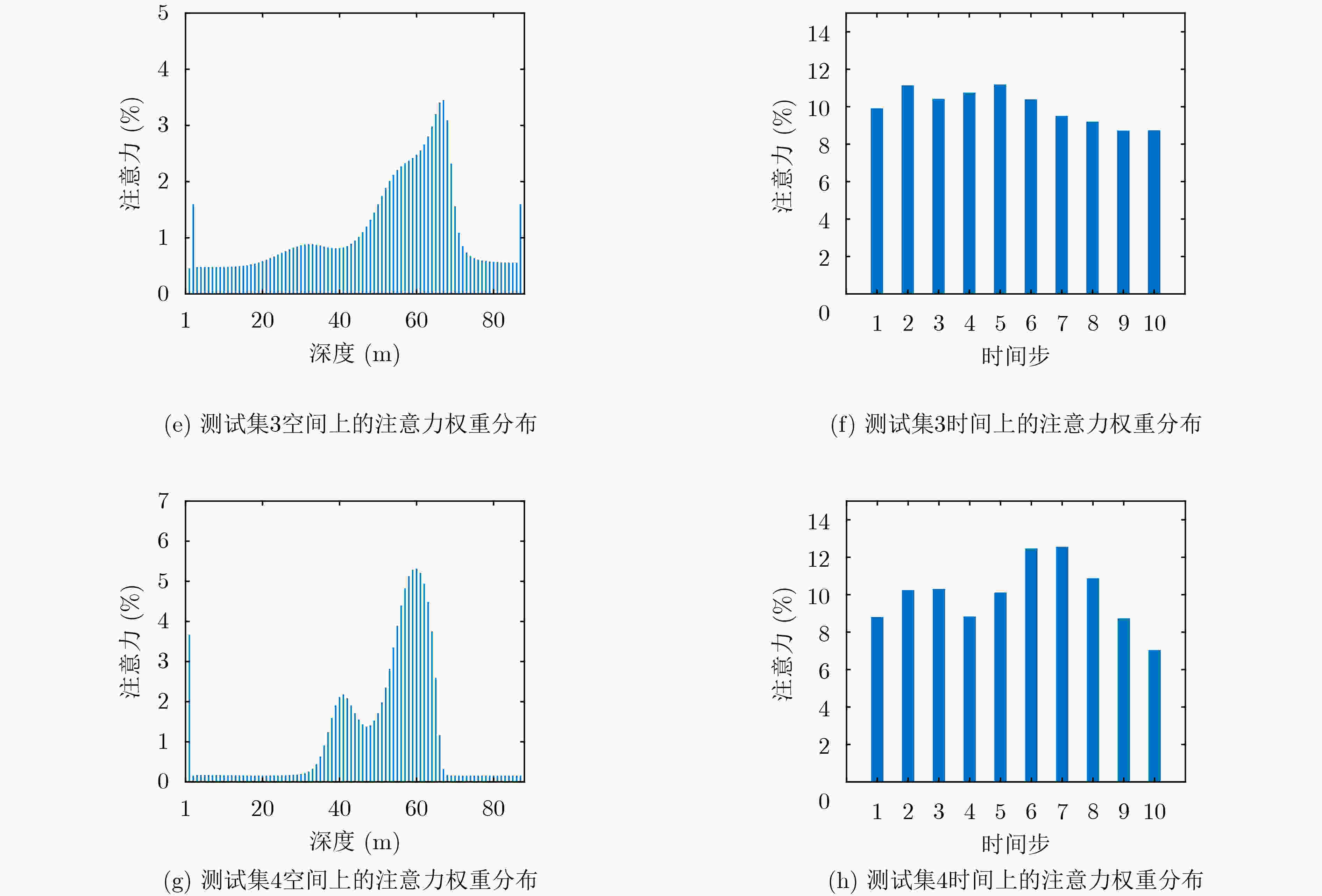
下载:
