一种基于三维可变换CNN加速结构的并行度优化搜索算法

屈心媛; 徐宇; 黄志洪; 蔡刚; 方震

doi:10.11999/JEIT210059

一种基于三维可变换CNN加速结构的并行度优化搜索算法

doi: 10.11999/JEIT210059

1.
中国科学院空天信息创新研究院北京 100190
2.
中国科学院大学电子电气与通信工程学院北京 100049

基金项目: 国家自然科学基金(61704173, 61974146)，北京市科技重大专项(Z171100000117019)

详细信息

作者简介:
屈心媛：女，1994年生，博士生，研究方向为基于FPGA的CNN加速器架构设计

徐宇：男，1990年生，博士，研究方向为大规模集成电路设计自动化

黄志洪：男，1984年生，高级工程师，研究方向为可编程芯片设计与FPGA硬件加速

蔡刚：男，1980年生，正高级工程师，硕士生导师，研究方向为集成电路设计、抗辐照加固设计、人工智能系统设计

方震：男，1976年生，研究员，博士生导师，研究方向为新型医疗电子及医学人工智能技术

通讯作者:
黄志洪　huangzhihong@mail.ie.ac.cn

¹⁾本节给出的数据均为基于KCU1500的AlexNet加速器的实验结果。²⁾ (Para_in=1, Para_seg=2)相当于Para_in=1/2；(Para_in=3, Para_seg=5)相当于Para_in=3/5；以此类推。
中图分类号: TN47
计量
- 文章访问数: 1048
- HTML全文浏览量: 412
- PDF下载量: 110
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-08
- 修回日期: 2021-08-04
- 网络出版日期: 2021-09-09
- 刊出日期: 2022-04-18

A Parallelism Strategy Optimization Search Algorithm Based on Three-dimensional Deformable CNN Acceleration Architecture

1.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
2.
School of Electronic, Electrical, and Communication Engineering, University of Chinese Academy of Sciences (UCAS), Beijing 100049, China

Funds: The National Natural Science Foundation of China (61704173, 61974146), The Major Program of Beijing Science and Technology (Z171100000117019)

摘要

摘要: 现场可编程门阵列(FPGA)被广泛应用于卷积神经网络(CNN)的硬件加速中。为优化加速器性能，Qu等人(2021)提出了一种3维可变换的CNN加速结构，但该结构使得并行度探索空间爆炸增长，搜索最优并行度的时间开销激增，严重降低了加速器实现的可行性。为此该文提出一种细粒度迭代优化的并行度搜索算法，该算法通过多轮迭代的数据筛选，高效地排除冗余的并行度方案，压缩了超过99%的搜索空间。同时算法采用剪枝操作删减无效的计算分支，成功地将计算所需时长从10⁶ h量级减少到10 s内。该算法可适用于不同规格型号的FPGA芯片，其搜索得到的最优并行度方案性能突出，可在不同芯片上实现平均(R1, R2)达(0.957, 0.962)的卓越计算资源利用率。
- 现场可编程门阵列 /
- 卷积神经网络 /
- 硬件加速
Abstract: Field Programmable Gate Array (FPGA) is widely used in Convolutional Neural Network (CNN) hardware acceleration. For better performance, a three-dimensional transformable CNN acceleration structure is proposed by Qu et al (2021). However, this structure brings an explosive growth of the parallelism strategy exploration space, thus the time cost to search the optimal parallelism has surged, which reduces severely the feasibility of accelerator implementation. To solve this issue, a fine-grained iterative optimization parallelism search algorithm is proposed in this paper. The algorithm uses multiple rounds of iterative data filtering to eliminate efficiently the redundant parallelism schemes, compressing more than 99% of the search space. At the same time, the algorithm uses pruning operation to delete invalid calculation branches, and reduces successfully the calculation time from 10⁶ h to less than 10 s. The algorithm can achieve outstanding performance in different kinds of FPGAs, with an average computing resource utilization (R1, R2) up to (0.957, 0.962).
- Field Programmable Gate Array (FPGA) /
- Convolutional Neural Network (CNN) /
- Hardware acceleration
¹⁾本节给出的数据均为基于KCU1500的AlexNet加速器的实验结果。²⁾ (Para_in=1, Para_seg=2)相当于Para_in=1/2；(Para_in=3, Para_seg=5)相当于Para_in=3/5；以此类推。

HTML全文

图 1 CNN加速器单层结构示意图

下载: 全尺寸图片幻灯片

图 2 矩阵卷积分段计算示意图

下载: 全尺寸图片幻灯片

图 3 β=0.20时，算法搜索的计算量随α的变化情况

下载: 全尺寸图片幻灯片

图 4 基于不同规格FPGA的AlexNet加速器性能随(α, β)变化色温图

下载: 全尺寸图片幻灯片

表 1 AlexNet网络结构参数

层	N_in	N_out	SIZE_in	SIZE_out	SIZE_ker	Stride	N_pad
CONV1	3	96	227	55	11	4	0
POOL1	96	96	55	27	3	2	0
CONV2	48	256	27	27	5	1	2
POOL2	256	256	27	13	3	2	0
CONV3	256	384	13	13	3	1	1
CONV4	192	384	13	13	3	1	1
CONV5	192	256	13	13	3	1	1
POOL5	256	256	13	6	3	2	0
FC1	9216	4096	1	1	–	–	–
FC2	4096	4096	1	1	–	–	–
FC3	4096	1000	1	1	–	–	–

下载: 导出CSV

表 2 不同FPGA CNN加速器的资源利用率

文献	VGG		文献	AlexNet
文献	R1	R2	文献	R1	R2
[5]	0.8	0.8	[3]	0.32	0.38
[11]	0.71	0.71	[4]	0.42	0.55
[14]	0.77	0.84	[6]	0.50	0.85
[8]	0.78	0.99	[8]	0.67	0.76
[15]	0.66	0.80	[14]	0.62	0.78

下载: 导出CSV

表 3 细粒度并行度迭代算法

输入：片上可用DSP数#DSP_limit、可用BRAM数量#BRAM_limit、CNN网络结构参数及α, β
输出：Para_in，Para_out及Para_seg
(1) 计算各层计算量#OP_i与网络总计算量#OP_total之比γ_i。
(2) 按照计算量分布比例将片上可用DSP分配给各层，各层分配到的DSP数#DSPⁱ_alloc←γ_i·#DSP_total
(3)根据计算总量和计算资源总数，算出理论最小计算周期数#cycle_baseline。
(4) 第i层，遍历Para_in，Para_out及ROW_out的所有离散可行取值(即3者定义域形成的笛卡儿积)，生成全组合情况下的并行度参数配置　　集S⁰_i，计算对应的#cycle_i、#BRAM_i与#DSP_i。
(5) 筛选满足α, β约束的数据集S_i。
S_i←select ele from S⁰_iwhere (#cycle_i/#cycle_baseline in [1–α,1+α] and #DSP_i/#DSPⁱ_alloc in [1–β,1+β])
(6)数据粗筛，集合S’_i：任意相邻的两个元素不存在“KO”偏序关系。
for i in range(5):
orders←[(cycle, dsp, bram), (dsp, cycle, bram), (bram, cycle, dsp)]
for k in range(3):
S_i.sort_ascend_by(orders[k])
p←0
for j in range(1, size(S_i)):
if σ_j KO σ_p then S_i.drop(σ_p), p←j
else S_i.drop(σ_j)
S’_i←S_i
(7)数据精筛，集合T_i：任意两个元素不存在“KO”偏序关系。
for i in range(5):
S’_i.sort_ascend_by((cycle,dsp,bram))
for j in range(1, size(S’_i)):
for k in range(j):
if σ_k KO σ_j then S’_i.drop(σ_j), break
T_i←S’_i
(8)搜索剪枝。
maxCycle←INT_MAX, dspUsed←0, bramUsed←0
def calc(i):
if i==5 then
update(maxCycle)
return
for j in range(size(T_i)):
tmpDsp←dspUsed+dsp^j_i, tmpBram←bramUsed+bram^j_i
if not(tmpDsp>dspTotal or tmpBram>bramTotal or
cycle^j_i≥maxCycle) then
dspUsed←tmpDsp, bramUsed←tmpBram
calc(i+1)
dspUsed←tmpDsp-dsp^j_i, bramUsed←tmpBram-bram^j_i
else
continue
calc(0)
(9)选出maxCycle（即min{max{#cycle_i}}）对应的并行度元素，输出约束条件下最优并行度的参数信息。

下载: 导出CSV

表 4 不同规格FPGA上AlexNet加速器资源利用率、计算量与计算时长

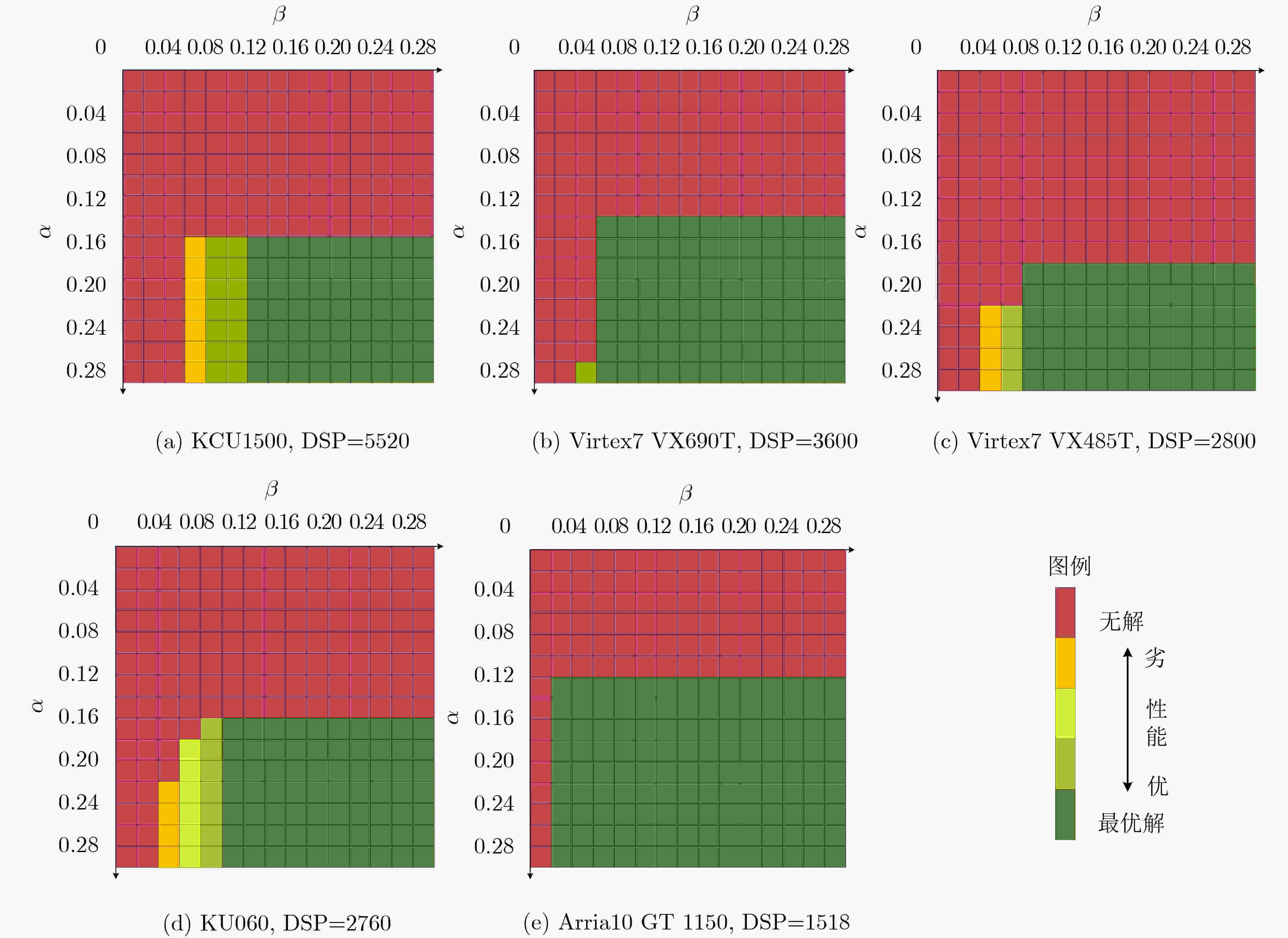
FPGA型号	DSP资源数	R1	R2	原始计算量	压缩比(%)	执行时间(s)
Arria10 GT 1150	1518	0.987	0.989	5.683×10⁷	99.892	1.544
KU060	2760	0.947	0.951	3.026×10⁸	99.979	6.444
Virtex7 VX485T	2800	0.936	0.941	9.903×10⁸	99.994	5.841
Virtex7 VX690T	3600	0.960	0.967	2.082×10⁸	99.998	2.775
KCU1500	5520	0.955	0.962	5.772×10⁹	99.999	8.115

下载: 导出CSV

表 5 AlexNet加速器性能对比

型号	文献[4]	文献[11]	文献[12]	文献[8]	本文
量化位宽	16 bit定点	16 bit定点	16 bit定点	16 bit定点	16 bit定点
频率(MHz)	250/500	200	150	220	230
FPGA型号	KCU1500	Arria10GX1150	ZynqXC7Z045	KCU1500	KCU1500
吞吐率(GOP/s)	2335.4	584.8	137.0	1633.0	2425.5
性能功耗比(GOP/s/W)	37.31	无数据	14.21	72.31	62.35
资源利用率(R1, R2)	(0.42, 0.55)	(0.48, 0.48)	(0.51, 0.59)	(0.67, 0.76)	(0.96, 0.96)

下载: 导出CSV

参考文献(15)

[1]	LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791
[2]	QU Xinyuan, HUANG Zhihong, XU Yu, et al. Cheetah: An accurate assessment mechanism and a high-throughput acceleration architecture oriented toward resource efficiency[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2021, 40(5): 878–891. doi: 10.1109/TCAD.2020.3011650
[3]	REGGIANI E, RABOZZI M, NESTOROV A M, et al. Pareto optimal design space exploration for accelerated CNN on FPGA[C]. 2019 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Rio de Janeiro, Brazil, 2019: 107–114. doi: 10.1109/IPDPSW.2019.00028.
[4]	YU Xiaoyu, WANG Yuwei, MIAO Jie, et al. A data-center FPGA acceleration platform for convolutional neural networks[C]. 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 2019: 151–158. doi: 10.1109/FPL.2019.00032.
[5]	LIU Zhiqiang, CHOW P, XU Jinwei, et al. A uniform architecture design for accelerating 2D and 3D CNNs on FPGAs[J]. Electronics, 2019, 8(1): 65. doi: 10.3390/electronics8010065
[6]	LI Huimin, FAN Xitian, JIAO Li, et al. A high performance FPGA-based accelerator for large-scale convolutional neural networks[C]. 2016 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Swiss, 2016: 1–9. doi: 10.1109/FPL.2016.7577308.
[7]	QIU Jiantao, WANG Jie, YAO Song, et al. Going deeper with embedded FPGA platform for convolutional neural network[C]. The 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, California, USA, 2016: 26–35.
[8]	ZHANG Xiaofan, WANG Junsong, ZHU Chao, et al. DNNBuilder: An automated tool for building high-performance DNN hardware accelerators for FPGAs[C]. 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Diego, USA, 2018: 1–8. doi: 10.1145/3240765.3240801.
[9]	LIU Zhiqiang, DOU Yong, JIANG Jingfei, et al. Automatic code generation of convolutional neural networks in FPGA implementation[C]. 2016 International Conference on Field-Programmable Technology (FPT), Xi’an, China, 2016: 61–68. doi: 10.1109/FPT.2016.7929190.
[10]	KRIZHEVSKY A, SUTSKEVER I, and HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84–90. doi: 10.1145/3065386
[11]	MA Yufei, CAO Yu, VRUDHULA S, et al. Optimizing the convolution operation to accelerate deep neural networks on FPGA[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2018, 26(7): 1354–1367. doi: 10.1109/TVLSI.2018.2815603
[12]	GUO Kaiyuan, SUI Lingzhi, QIU Jiantao, et al. Angel-Eye: A complete design flow for mapping CNN onto embedded FPGA[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018, 37(1): 35–47. doi: 10.1109/TCAD.2017.2705069
[13]	ZHANG Chen, SUN Guangyu, FANG Zhenman, et al. Caffeine: Toward uniformed representation and acceleration for deep convolutional neural networks[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(11): 2072–2085. doi: 10.1109/TCAD.2017.2785257
[14]	ZHANG Jialiang and LI Jing. Improving the performance of OpenCL-based FPGA accelerator for convolutional neural network[C]. The 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, California, USA, 2017: 25–34. doi: 10.1145/3020078.3021698.
[15]	LIU Zhiqiang, DOU Yong, JIANG Jingfei, et al. Throughput-optimized FPGA accelerator for deep convolutional neural networks[J]. ACM Transactions on Reconfigurable Technology and Systems, 2017, 10(3): 17. doi: 10.1145/3079758