Lawson-norm Constrained Generalized Lncosh Based Adaptive Algorithm for Sparse System Identification
-
摘要: 该文提出一种通用稀疏系统识别Lawson-lncosh自适应滤波算法,该算法采用系数向量的Lawson范数和误差的lncosh函数构建代价函数。Lawson范数约束引入参数p,实现稀疏约束滤波动态调整,所提算法可以提高稀疏系统识别时的收敛速度,减小了稳态误差。误差的lncosh函数具有良好的抗脉冲噪声性能。然后,算法分析了步长参数的取值范围和参数p对算法性能的影响。计算机仿真结果表明,在高斯信号输入和色信号输入情况下,所提算法的性能要明显优于其他现存算法,且具备稀疏约束可控特性。Abstract: A generalized Lawson-lncosh adaptive filtering algorithm for sparse system identification is proposed. The proposed algorithm is derived by constructing a new cost function consisted of Lawson-norm of system coefficient vector and lncosh function of instantaneous error. And the Lawson-norm constraint introduces a parameter p which can realize the dynamic adjustment of sparsity. The proposed algorithm can improve the convergence speed and reduce the steady-state error for sqarse system identification, where the Lncosh function of the error has the property of combating impulsive noise. Then, the range of the step-size and effect of parameter p on the proposed algorithm are analyzed. Computer simulation results show that the proposed algorithm has superior performance compared with other existing algorithms with Gaussian and colored input signals and the sparsity constraint for the proposed algorithm is controllable.
-
Key words:
- Sparse system identification /
- Adaptive filtering /
- Lawson norm /
- Impulsive noise
-
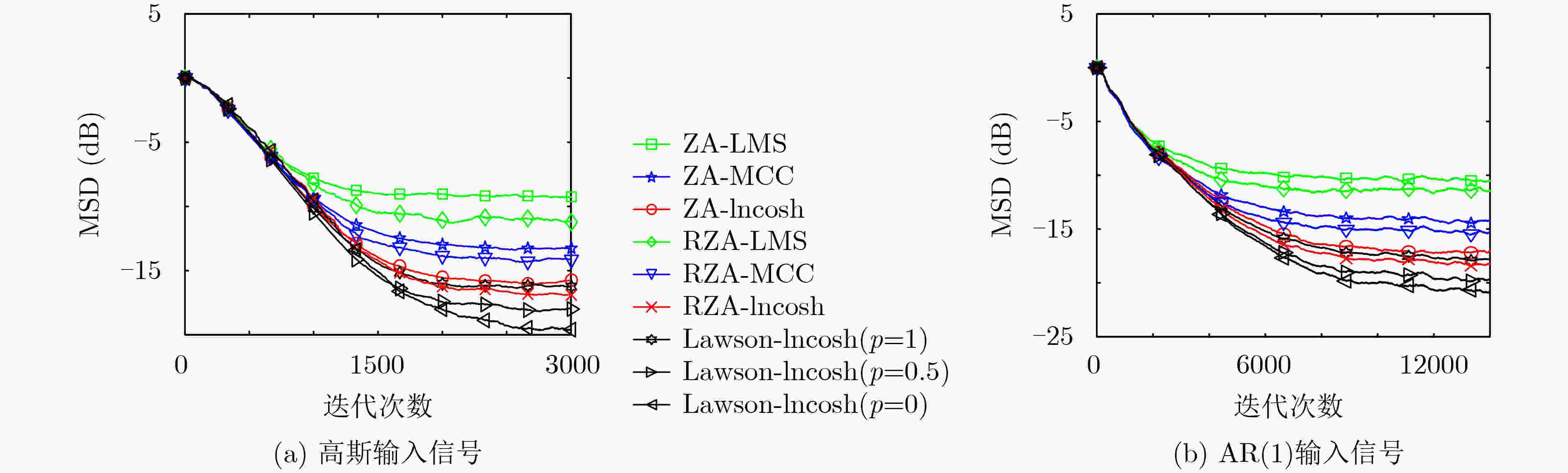
表 1 实验4各算法参数
算法 $\mu $(高斯输入) $\eta $(高斯输入) $\mu $(AR输入) $\eta $(AR输入) ZA-LMS 0.0020 0.000008 0.002 0.0000100 RZA-LMS 0.0020 0.000040 0.002 0.0000300 ZA-MCC 0.0020 0.000005 0.002 0.0000050 RZA-MCC 0.0022 0.000020 0.002 0.0000100 ZA-lncosh 0.0024 0.000005 0.002 0.0000100 RZA-lncosh 0.0024 0.000010 0.002 0.0000040 Lawson-lncosh(p=1) 0.0024 0.000008 0.002 0.0000030 Lawson-lncosh(p=0.5) 0.0024 0.000003 0.002 0.0000010 Lawson-lncosh(p=0) 0.0024 0.000004 0.002 0.0000004 -
[1] DINIZ P S R. Adaptive Filtering Algorithms and Practical Implementation[M]. 3rd ed. New York: Springer, 2008: 77–126. [2] WIDROW B and STEARNS S D. Adaptive Signal Processing[M]. New Jersey: Prentice Hall, 1985: 99–116. [3] CHEN Yilun, GU Yuantao, and HERO A O. Sparse LMS for system identification[C]. 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, China, 2009: 3125–3128. [4] 曲庆, 金坚, 谷源涛. 用于稀疏系统辨识的改进l0-LMS算法[J]. 电子与信息学报, 2011, 33(3): 604–609.QU Qing, JIN Jian, and GU Yuantao. An improved l0-LMS algorithm for sparse system identification[J]. Journal of Electronics &Information Technology, 2011, 33(3): 604–609. [5] GU Yuantao, JIN Jian, and MEI Shunliang. l0 norm constraint LMS algorithm for sparse system identification[J]. IEEE Signal Processing Letters, 2009, 16(9): 774–777. doi: 10.1109/LSP.2009.2024736 [6] WANG Chengcheng, ZHANG Yonggang, WEI Ye, et al. A new l0-LMS algorithm with adaptive zero attractor[J]. IEEE Communications Letters, 2015, 19(12): 2150–2153. doi: 10.1109/LCOMM.2015.2490665 [7] ZHAO Haiquan and WANG Wenyuan. Volterra system identification under maximum correntropy criteria in impulsive environments[C]. The 2016 35th Chinese Control Conference (CCC), Chengdu, China, 2016: 5067–5070. [8] LI Yingsong, JIANG Zhengxiong, SHI Wanlu, et al. Blocked maximum correntropy criterion algorithm for cluster-sparse system identifications[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 66(11): 1915–1919. doi: 10.1109/TCSII.2019.2891654 [9] SUN Zeyang, LI Yingsong, JIANG Zhengxiong, et al. Active coefficient detection maximum correntropy criterion algorithm for sparse channel estimation under non-Gaussian environments[J]. IEEE Access, 2019, 7: 151867–151877. doi: 10.1109/ACCESS.2019.2924028 [10] LIU Chang and JIANG Ming. Robust adaptive filter with lncosh cost[J]. Signal Processing, 2020, 168: 107348. doi: 10.1016/j.sigpro.2019.107348 [11] SUN Zeyang, LI Yingsong, LI Yibing, et al. Steady-state mean-square error analysis for non-negative least lncosh algorithm[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(6): 2237–2241. doi: 10.1109/TCSII.2020.3048287 [12] MSALMAN M S, ELSAYED F, RASHDAN M, et al. A zero-attracting sparse lncosh adaptive algorithm[C]. The 2020 IEEE 40th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 2020: 565–568. doi: 10.1109/ELNANO50318.2020.9088847. [13] SHANG Wenjing, XUE Wei, LI Yingsong, et al. Improved primal–dual interior-point method using the Lawson-norm for inverse problems[J]. IEEE Access, 2020, 8: 41053–41061. doi: 10.1109/ACCESS.2020.2976727 [14] KOH T and POWERS E. Efficient methods of estimate correlation functions of Gaussian processes and their performance analysis[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(4): 1032–1035. doi: 10.1109/TASSP.1985.1164623 [15] 金坚, 谷源涛, 梅顺良. 用于稀疏系统辨识的零吸引最小均方算法[J]. 清华大学学报: 自然科学版, 2010, 50(10): 1656–1659. doi: 10.16511/j.cnki.qhdxxb.2010.10.009JIN Jian, GU Yuantao, and MEI Shunliang. Adaptive algorithm for sparse system identification: Zero-attracting LMS[J]. Journal of Tsinghua University:Science &Technology, 2010, 50(10): 1656–1659. doi: 10.16511/j.cnki.qhdxxb.2010.10.009 [16] DAS R L and NARWARIA M. Lorentzian based adaptive filters for impulsive noise environments[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2017, 64(6): 1529–1539. doi: 10.1109/TCSI.2017.2667705 [17] QIAN Guobing, WANG Shiyuan, and IU H H C. Maximum total complex correntropy for adaptive filter[J]. IEEE Transactions on Signal Processing, 2020, 68: 978–989. doi: 10.1109/TSP.2020.2969042 -





 下载:
下载:



 下载:
下载:
