The Constructions of Optimal Balanced Quadriphase Almost Mismatched Complementary Pairs with Prime Length
-
摘要: 当一对失配序列的所有异相自相关函数和均为同一非0整数时,称该对失配序列为几乎失配互补对。该文提出平衡4元几乎失配互补对的新类型序列,通过Gray映射证明得到了平衡的素数长4元几乎失配互补对的理论界,基于4阶分圆类,提出满足理论界的周期为素数长的理想平衡4元几乎失配互补对的构造方法。通过该文研究扩大了4元互补对的存在范围,弥补了目前已有4元互补对大多只存在偶数长度的缺陷。Abstract: A pair of mismatched sequences is called an almost mismatched complementary pair if their periodic autocorrelation functions sum up to a same nonzero integer for all out-of-phase time shifts. In this paper, a new balanced quadriphase almost mismatched complementary pair is proposed, the theoretical bound of balanced quadriphase almost complementary pair with prime length is proved by Gray mapping, based on the cyclotomic classes of order 4, the optimal balanced quadriphase almost mismatched complementary pair with prime length satisfied theoretical bound is constructed. The existence of quadriphase complementary pairs are expanded and compensated the deficiency of most of the existing ones only have even length at present by investigate in this paper.
-
表 1
$p$ 为偶数时,4阶分圆数及计算式${(c,d)_4}$ $s \equiv 1(\boldsymbolod 4)$ $s \equiv 3(\boldsymbolod 4)$ ${(0,0)_4}$ $(Q - 11 - 6s)/16$ $(Q - 11 + 6s)/16$ ${(0,1)_4},{(1,0)_4},{(3,3)_4}$ $(Q - 3 + 2s + 8t)/16$ $(Q - 3 - 2s + 8t)/16$ ${(0,2)_4},{(2,0)_4},{(2,2)_4}$ $(Q - 3 + 2s)/16$ $(Q - 3 - 2s)/16$ ${(0,3)_4},{(1,1)_4},{(3,0)_4}$ $(Q - 3 + 2s - 8t)/16$ $(Q - 3 - 2s - 8t)/16$ $\begin{array}{l} {(1,2)_4},{(1,3)_4},{(2,1)_4}, \\ {(2,3)_4},{(3,1)_4},{(3,2)_4} \\ \end{array} $ $(Q + 1 - 2s)/16$ $(Q + 1 + 2s)/16$ 表 2
$p$ 为奇数时,4阶分圆数及计算式$(c,d){ _4}$ $s \equiv 1(\boldsymbolod 4)$ $s \equiv 3(\boldsymbolod 4)$ ${(0,2)_4}$ $(Q + 1 - 6s)/16$ $(Q + 1 + 6s)/16$ ${(0,0)_4},{(2,0)_4},{(2,2)_4}$ $(Q - 7 + 2s)/16$ $(Q - 7 - 2s)/16$ ${(0,1)_4},{(1,3)_4},{(3,2)_4}$ $(Q + 1 + 2s - 8t)/16$ $(Q + 1 - 2s - 8t)/16$ ${(0,3)_4},{(1,2)_4},{(3,1)_4}$ $(Q + 1 + 2s + 8t)/16$ $(Q + 1 - 2s + 8t)/16$ $\begin{array}{l} {(1,0)_4},{(1,1)_4},{(2,1)_4}, \\ {(2,3)_4},{(3,0)_4},{(3,3)_4} \\ \end{array} $ $ (Q - 3 - 2s)/16$ $(Q - 3 + 2s)/16$ 表 3
$p$ 为奇数时,平衡4元失配序列$({x_1},{y_1})$ 与$({x_2},{y_2})$ 的定义参数$[({j_1},{k_1},{l_1},{r_1}),(j_1',k_1',l_1',r_1'),({j_2},{k_2},{l_2},{r_2}),(j_2',k_2',l_2',r_2')]$ $[({x_1}(0),{y_1}(0)),({x_2}(0),{y_2}(0))] \in $ $[((0,2,1,3),(0,2,1,3)),((0,2,1,3),(0,2,1,3))]$ $\begin{array}{*{20}{l} }{\{ [(1, - 1),( - 1,1)];[({\rm{i}}, - {\rm{i}}),( - {\rm{i}},{\rm{i}})];}\\{[({\rm{i}},1),(1, - {\rm{i}})];[( - {\rm{i}}, - 1),( - 1,{\rm{i}})];}\\{[(1,{\rm{i}}),( - 1, - {\rm{i}})];[({\rm{i}}, - 1),( - {\rm{i}},1)]\} }\end{array}$ $[((0,2,1,3),(0,2,1,3)),((0,2,3,1),(0,2,3,1))]$ $\begin{array}{*{20}{l} }{\{ [(1, - {\rm{i}}),({\rm{i}},1)];[( - 1,{\rm{i}}),( - {\rm{i}}, - 1)];}\\{[({\rm{i}},1),(1, - {\rm{i}})];[( - {\rm{i}}, - 1),( - 1,{\rm{i}})];}\\{[(1,{\rm{i}}),( - {\rm{i}},1)];[( - 1, - {\rm{i}}),({\rm{i}}, - 1)];}\\{[({\rm{i}}, - 1),( - 1, - {\rm{i}})];[( - {\rm{i}},1),(1,{\rm{i}})]\} }\end{array}$ 表 4
$p$ 为偶数时,平衡4元失配序列$({x_1},{y_1})$ 与$({x_2},{y_2})$ 的定义参数$[({j_1},{k_1},{l_1},{r_1}),(j_1',k_1',l_1',r_1'),({j_2},{k_2},{l_2},{r_2}),(j_2',k_2',l_2',r_2')]$ $[({x_1}(0),{y_1}(0)),({x_2}(0),{y_2}(0))] \in $ $[((0,2,1,3),(0,2,1,3)),((0,2,1,3),(0,2,1,3))]$ $\begin{array}{*{20}{l} }{\{ [(1, - 1),( - 1,1)];[({\rm{i}}, - {\rm{i}}),( - {\rm{i}},{\rm{i}})];}\\{[(1, - {\rm{i}}),( - 1,{\rm{i}})];[({\rm{i}},1),( - {\rm{i}}, - 1)];}\\{[(1,{\rm{i}}),( - 1, - {\rm{i}})];[({\rm{i}}, - 1),( - {\rm{i}},1)]\} }\end{array}$ $[((0,2,1,3),(0,2,1,3)),((0,2,3,1),(0,2,3,1))]$ $\begin{array}{*{20}{l} }{\{ [(1, - 1),(1, - 1)];[( - 1,1),( - 1,1)];}\\{[({\rm{i} }, - {\rm{i} }),( - {\rm{i} },{\rm{i} })];[( - {\rm{i} },{\rm{i} }),({\rm{i} }, - {\rm{i} })];}\\{[(1, - {\rm{i} }),( - {\rm{i} }, - 1)];[( - 1,{\rm{i} }),({\rm{i} },1)];}\\{[({\rm{i} },1),( - 1,{\rm{i} })];[( - {\rm{i} }, - 1),(1, - {\rm{i} })];}\\{[(1,{\rm{i} }),({\rm{i} }, - 1)];[( - 1, - {\rm{i}}),( - {\rm{i} },1)];}\\{[({\rm{i} }, - 1),(1,{\rm{i} })];[( - {\rm{i} },1),( - 1, - {\rm{i} })]\} }\end{array}$ $[((0,1,2,3),(0,1,2,3)),((0,3,1,2),(0,3,1,2))]$ $\begin{array}{*{20}{l} }{\{ [({\rm{i}},1),( - 1,{\rm{i}})];[( - {\rm{i}}, - 1),(1, - {\rm{i}})];}\\{[(1,{\rm{i}}),({\rm{i}}, - 1)];[( - 1, - {\rm{i}}),( - {\rm{i}},1)]\} }\end{array}$ $[((0,1,2,3),(0,1,2,3)),((0,3,2,1),(0,3,2,1))]$ $\begin{array}{*{20}{l} }{\{ [({\rm{i}},1),( - {\rm{i}}, - 1)];[( - {\rm{i}}, - 1),({\rm{i}},1)];}\\{[(1,{\rm{i}}),( - 1, - {\rm{i}})];[( - 1, - {\rm{i}}),(1,{\rm{i}})]\} }\end{array}$ 表 5 4元周期互补对已有结果总结
文献 周期长度 方法 平衡性 文献[15,20] 2, 4, 8, 10, 16, 20, 26, 32, 34, 40, ··· Gray映射,交织操作 不平衡 文献[21,22] 2, 3, 4, 5, 6, 8, 10, 11, 12, 13, 16, 18,
20, 22, 24, 26, 30, 32, 36, 40, 44, 48, ···Gray阵列扩展
Baker序列不平衡 文献[23] 3, 5, 7, 9, 11, 13, ···, 41, 43, 45, 49
4, 6, 8, 10, ···, 30, 34, 36, 38, ···Gray映射
生成序列扩展不平衡 定理2 素数长$ Q=4p+1, p$为奇数 4阶分圆 平衡 定理3 素数长$ Q=4p+1, p$为偶数 4阶分圆 平衡 -
[1] FAN Pingzhi and DARNELL M. Sequence Design for Communications Applications[M]. Taunton, England: Research Studies Press LTD, 1996: 3–16. [2] PARRAUD P. On the non-existence of (almost-) perfect Quaternary sequences[C]. 14th International Symposium on Applied Algebra, Algebraic Algorithms and Error-Correcting Codes, Melbourne, Australia, 2001: 210–218. [3] SCHOLTZ R and WELCH L. GMW sequences (Corresp.)[J]. IEEE Transactions on Information Theory, 1984, 30(3): 548–553. doi: 10.1109/TIT.1984.1056910 [4] JANG J W, KIM Y S, KIM S H, et al. New sequences with ideal autocorrelation constructed from binary sequences with ideal autocorrelation[C]. IEEE International Symposium on Information Theory, Seoul, Korea, 2009: 278–281. doi: 10.1109/ISIT.2009.5205807. [5] LUKE H D. Binary odd-periodic complementary sequences[J]. IEEE Transactions on Information Theory, 1997, 43(1): 365–367. doi: 10.1109/18.567768 [6] 李琦, 李鼎, 高军萍, 等. 零相关区屏蔽四元周期互补序列偶集设计研究[J]. 电子与信息学报, 2016, 38(2): 318–324. doi: 10.11999/JEIT150636LI Qi, LI Ding, GAO Junping, et al. Design of zero correlation zone punctured periodic complementary sequence pairs sets[J]. Journal of Electronics &Information Technology, 2016, 38(2): 318–324. doi: 10.11999/JEIT150636 [7] 李玉博, 许成谦, 李刚. 基于二元二值序列构造四元低相关区序列集[J]. 电子与信息学报, 2012, 34(5): 1174–1178. doi: 10.3724/SP.J.1146.2011.00980LI Yubo, XU Chengqian, and LI Gang. Construction of low correlation zone sequence set using binary sequence with ideal two-level autocorrelation[J]. Journal of Electronics &Information Technology, 2012, 34(5): 1174–1178. doi: 10.3724/SP.J.1146.2011.00980 [8] ARASU K T, ARYA D, and BAKSHI A. Constructions of punctured difference set pairs and their corresponding punctured binary array Pairs[J]. IEEE Transactions on Information Theory, 2015, 61(4): 2191–2199. doi: 10.1109/TIT.2015.2403857 [9] SHEN Xiumin, JIA Yanguo, and SONG Xiaofei. Constructions of binary sequence pairs of period 3p with optimal three-level correlation[J]. IEEE Communications Letters, 2017, 21(10): 2150–2153. doi: 10.1109/LCOMM.2017.2700845 [10] PENG Xiuping, XU Chengqian, and ARASU K T. New families of binary sequence pairs with two-level and three-level correlation[J]. IEEE Transactions on Information Theory, 2012, 58(11): 6968–6978. doi: 10.1109/TIT.2012.2210025 [11] PENG Xiuping, XU Chengqian, and LI Yubo. Mismatched binary periodic complementary pairs with period 3q[C]. Ninth International Workshop on Signal Design and its Applications in Communications (IWSDA), Dongguan, China, 2019: 1-5. doi: 10.1109/IWSDA46143.2019.8966097. [12] SHEN Xiumin, JIA Yanguo, WANG Jiaqi, et al. New families of balanced sequences of even period with three-level optimal autocorrelation[J]. IEEE Communications Letters, 2017, 21(10): 2146–2149. doi: 10.1109/LCOMM.2017.2661750 [13] 刘涛, 许成谦, 李玉博. 基于差族构造高斯整数周期互补序列[J]. 电子与信息学报, 2019, 41(5): 1167–1172. doi: 10.11999/JEIT180646LIU Tao, XU Chengqian, and LI Yubo. Constructions of Gaussian integer periodic complementary sequences based on difference families[J]. Journal of Electronics &Information Technology, 2019, 41(5): 1167–1172. doi: 10.11999/JEIT180646 [14] ADHIKARY A R, LIU Zilong, GUAN Yongliang, et al. Optimal binary periodic almost-complementary pairs[J]. IEEE Signal Processing Letters, 2016, 23(12): 1816–1820. doi: 10.1109/LSP.2016.2600586 [15] JANG J W, KIM Y S, KIM S H, et al. New construction methods of periodic complementary sequence sets[J]. Advances in Mathematics of Communications, 2010, 4(1): 61–68. doi: 10.3934/amc.2010.4.61 [16] TANG Xiaohu and DING Cunsheng. New classes of balanced and almost balanced binary sequences with optimal autocorrelation value[J]. IEEE Transactions on Information Theory, 2010, 56(12): 6398–6405. doi: 10.1109/TIT.2010.2081170 [17] CUSICK T W, DING Cunsheng, and RENVALL A. Stream Ciphers and Number Theory[M]. Amsterdam: Elsevier, 1998. [18] 李玉博, 许成谦, 李刚, 等. 四元零相关区周期互补序列集构造法[J]. 电子与信息学报, 2013, 35(9): 2180–2186. doi: 10.3724/SP.J.1146.2012.01303LI Yubo, XU Chengqian, LI Gang, et al. Constructions of periodic complementary sequence sets with zero correlation zone[J]. Journal of Electronics &Information Technology, 2013, 35(9): 2180–2186. doi: 10.3724/SP.J.1146.2012.01303 [19] 许成谦. 差集偶与最佳二进阵列偶的组合研究方法[J]. 电子学报, 2001, 29(1): 87–89. doi: 10.3321/j.issn:0372-2112.2001.01.024XU Chengqian. Differences set pairs and approach for the study of perfect binary array pairs[J]. Acta Electronica Sinica, 2001, 29(1): 87–89. doi: 10.3321/j.issn:0372-2112.2001.01.024 [20] ZENG Fanxin, ZENG Xiaoping, ZHANG Zhenyu, et al. Quaternary periodic complementary/Z-complementary sequence sets based on interleaving technique and Gray mapping[J]. Advances in Mathematics of Communications, 2012, 6(2): 237–247. doi: 10.3934/amc.2012.6.237 [21] GIBSON R G and JEDWAB J. Quaternary Golay sequence pairs I: Even length[J]. Designs, Codes and Cryptography, 2011, 59(1/3): 131–146. doi: 10.1007/s10623-010-9471-z [22] GIBSON R G and JEDWAB J. Quaternary Golay sequence pairs II: Odd length[J]. Designs, Codes and Cryptography, 2011, 59(1/3): 147–157. doi: 10.1007/s10623-010-9472-y [23] ZHOU Zhengchun, LI Jiangdong, YANG Yang, et al. Two constructions of periodic complementary pairs[J]. IEEE Communications Letters, 2018, 22(12): 2507–2510. doi: 10.1109/LCOMM.2018.2876530 -





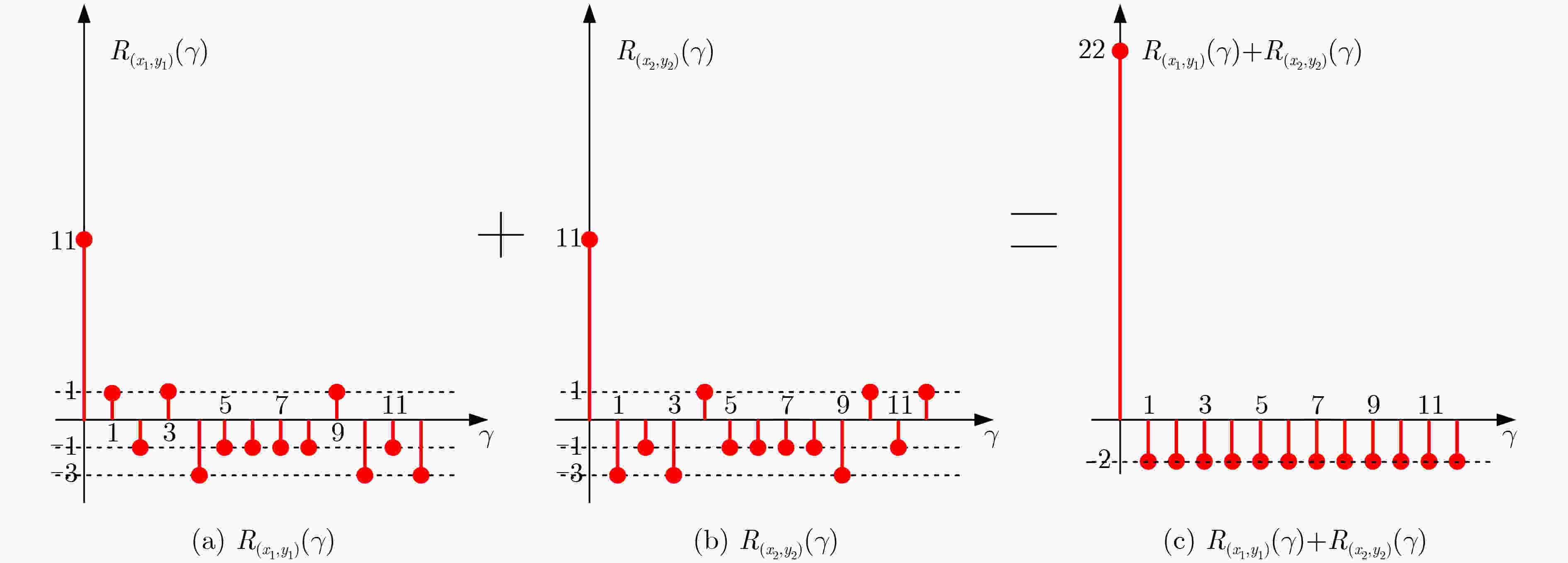


 下载:
下载:
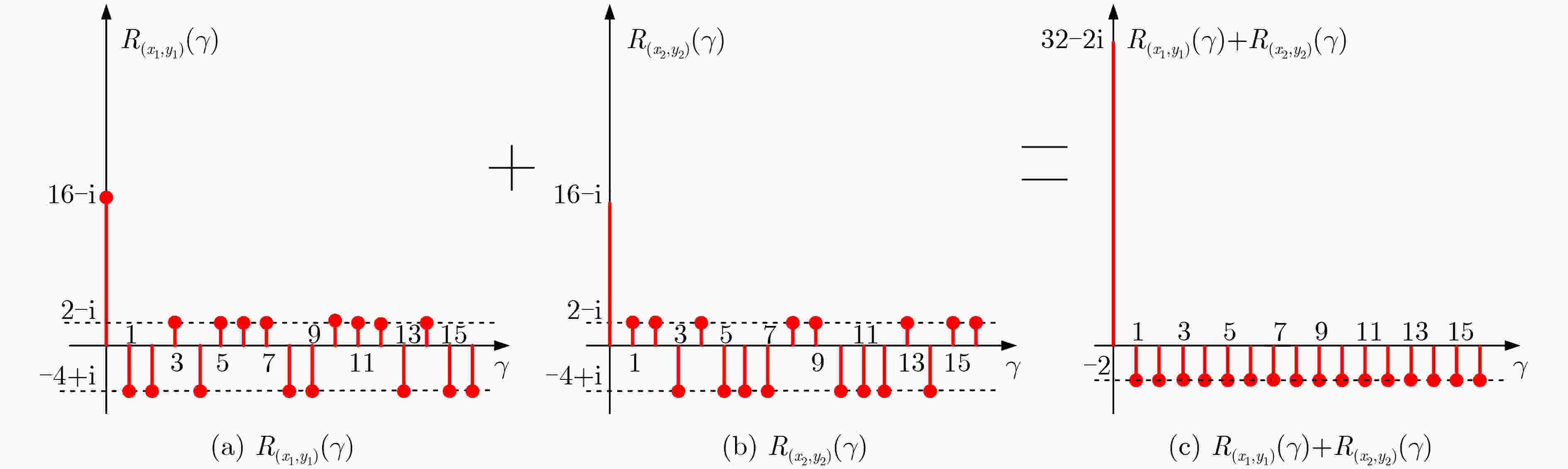












 下载:
下载:
