An Outlier Cleaning Algorithm Based on Deep Learning
-
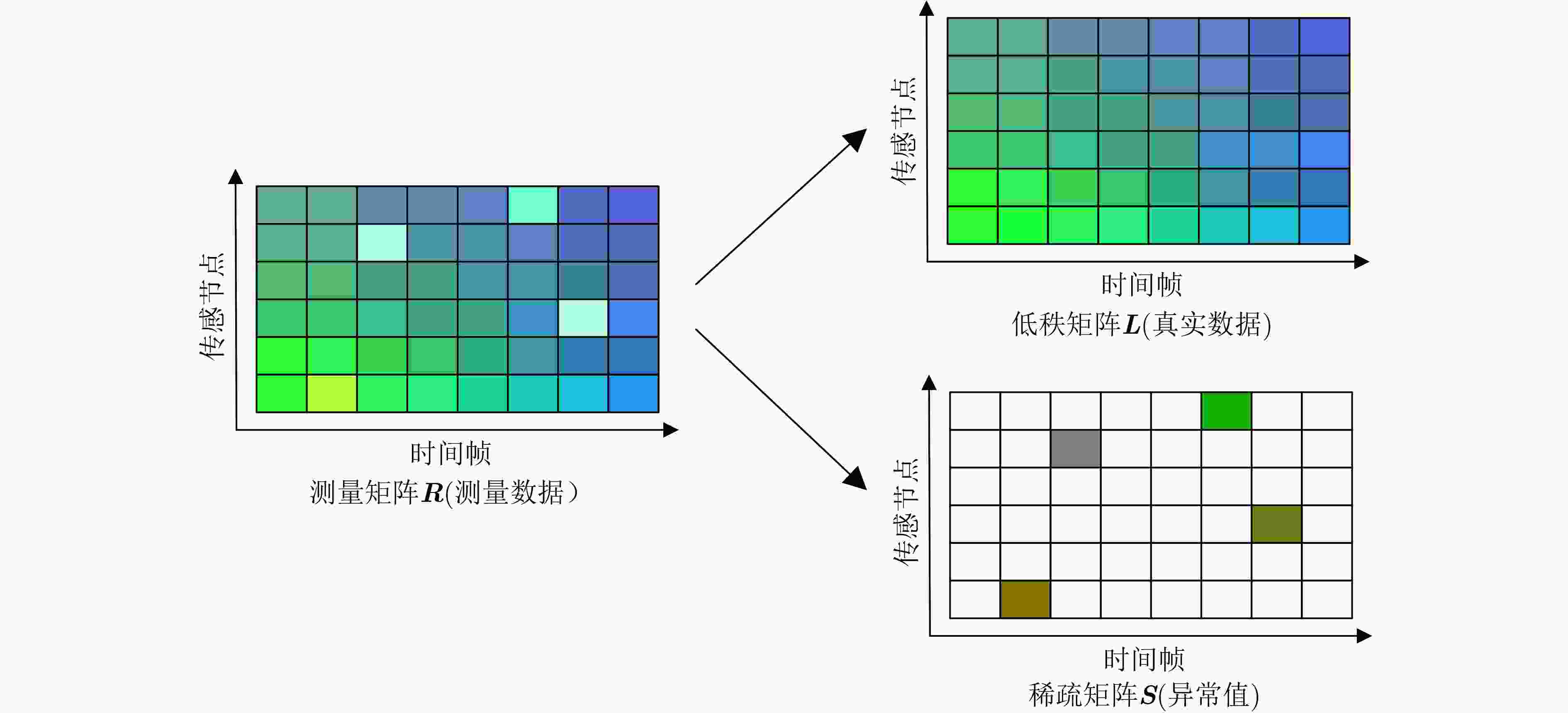
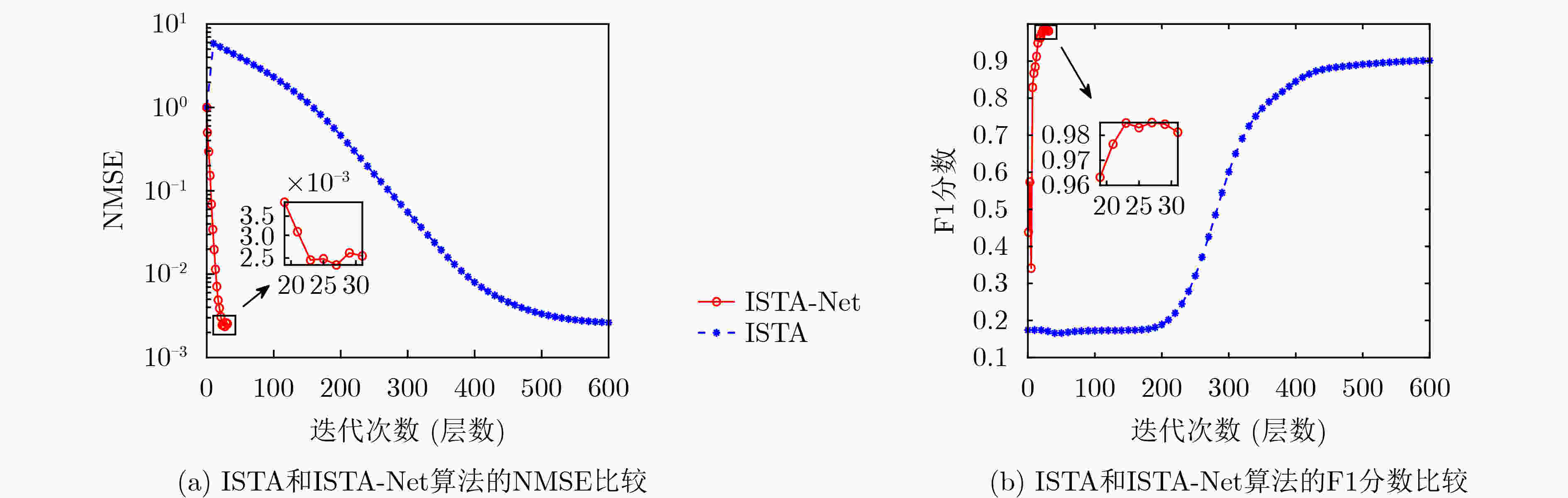
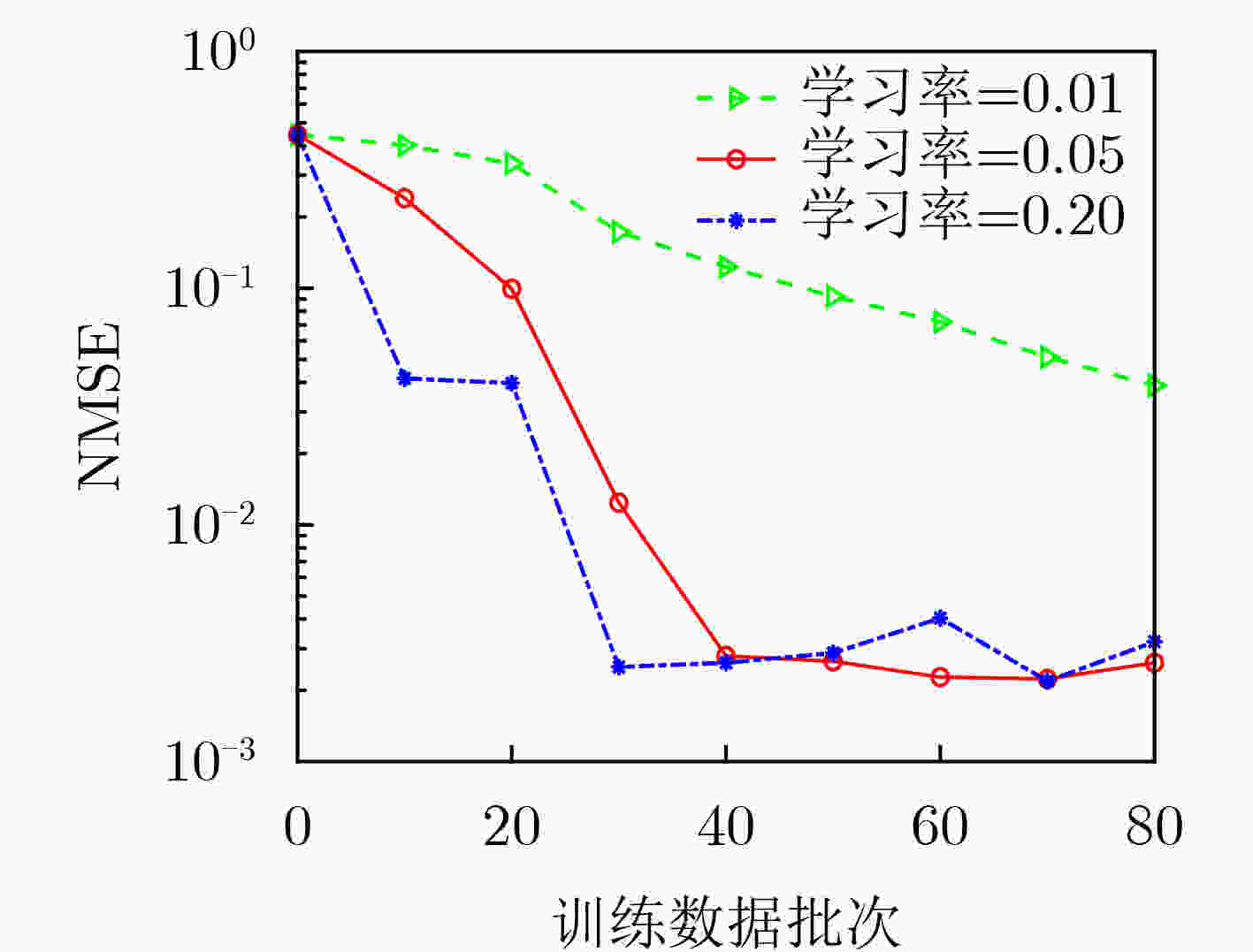
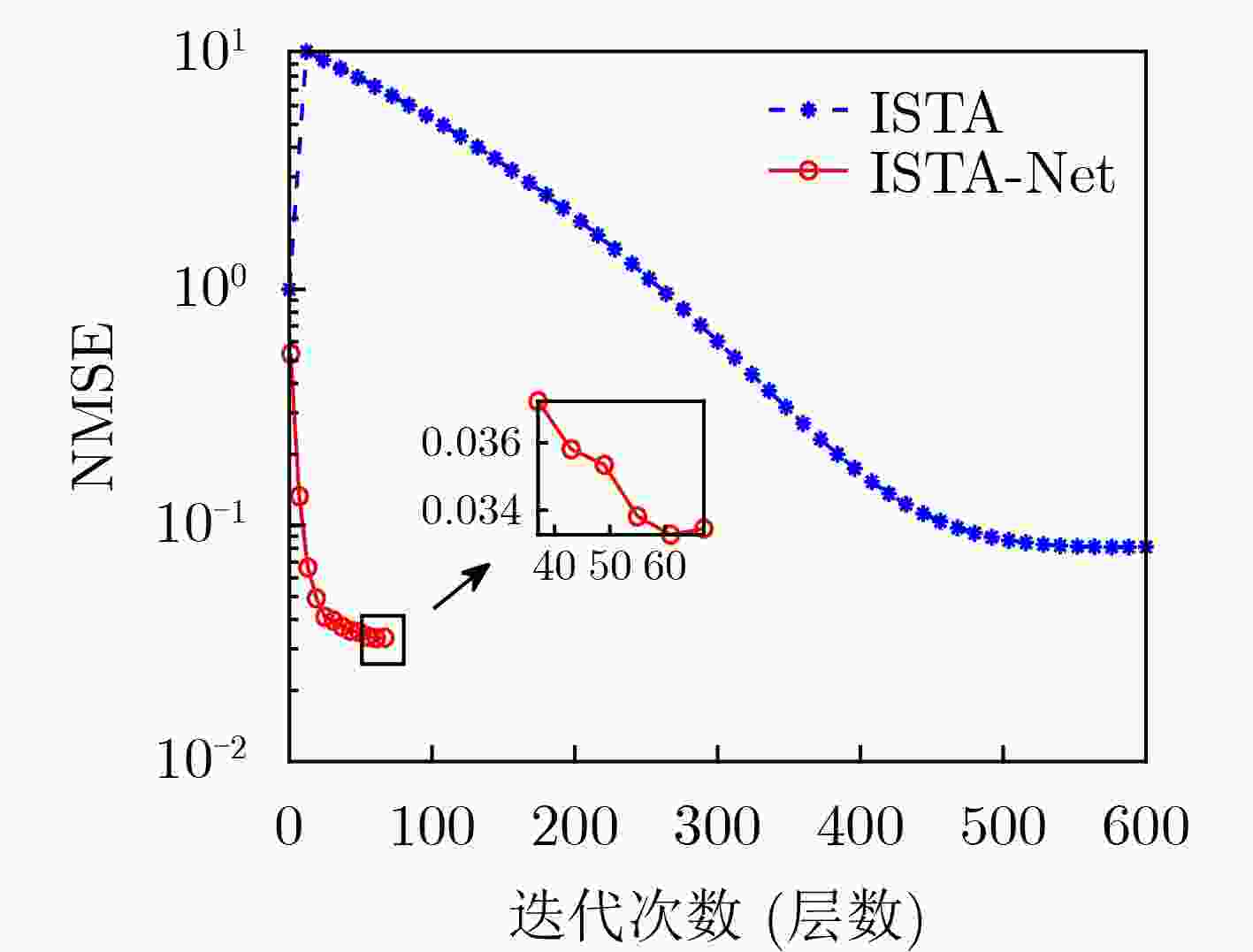
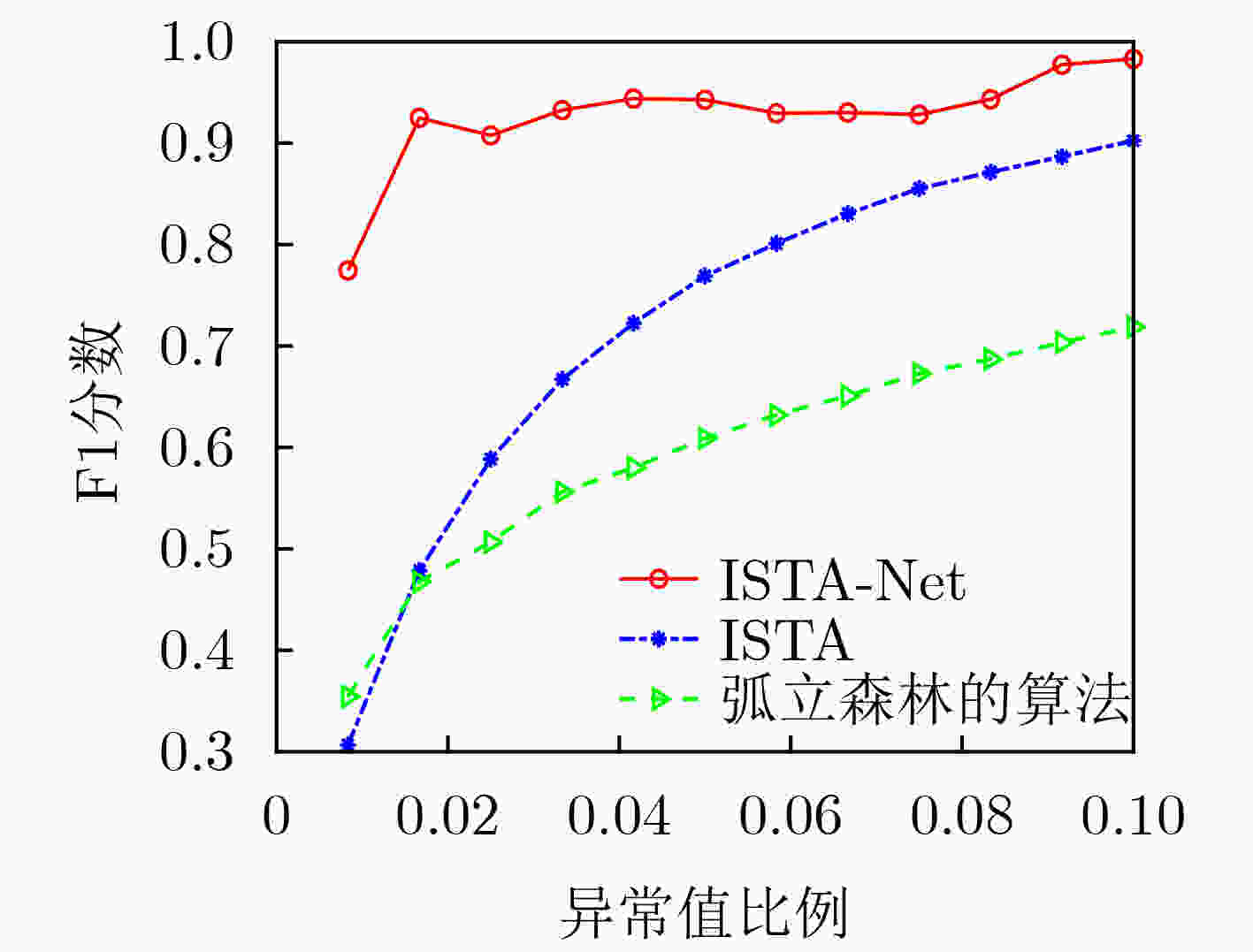
摘要: 在物联网(IoT)中采用合适的异常数据清洗算法能极大地提升数据质量。许多研究人员采用统计学方法或分类聚类等方法对时-空相关数据进行清洗。但这些方法需要额外的先验知识,会给汇聚节点带来额外的计算开销。该文根据低秩-稀疏矩阵分解模型,提出一种基于深度神经网络的快速异常数据清洗算法,来解决物联网中时-空相关数据的清洗问题。结合感知数据的时-空相关性和异常值的稀疏性,将异常数据清洗问题转换为优化问题,并采用迭代阈值收缩算法(ISTA)求解该优化问题,再将ISTA算法展开成一个固定长度的深度神经网络。实际数据集的实验结果表明,该方法能够自动更新阈值,比传统的ISTA算法收敛速度更快,精度更高。Abstract: The use of appropriate abnormal data cleaning algorithms in the Internet of Things (IoT) can greatly improve data quality. Statistical methods or clustering methods are utilized to clean anomalies in Spatio-temporal data. However, these methods require additional prior knowledge, which will incur additional computational overhead for the sink node. In this paper, in line with the low-rank sparse matrix decomposition model, a fast anomaly cleaning algorithm based on a deep neural network is proposed to solve the Spatio-temporal data cleaning problem in IoT. Both the Spatio-temporal correlation of sensing data and the abnormal values' sparsity are considered in an optimization problem. The Iterative Shrinkage-Thresholding Algorithm (ISTA) is used to solve it. Then the ISTA is unfolded into a fixed-length deep neural network. The real-world dataset’s experimental results show that the proposed method can automatically update the thresholds faster and more accurately than the traditional ISTA.
-
表 1 ISTA-Net异常数据恢复算法
已知:测量矩阵${\boldsymbol{R}}$,深度神经网络层数$K$ (1) 初始化 $ {\boldsymbol{S}}{\text{ = }}{\boldsymbol{L}}{\text{ = }}{\boldsymbol{0}} $,${\lambda _1} > 0$,${\lambda _2} > 0$ (2) for 数据集中的每个样本 do (3) 初始化 $ {{\boldsymbol{L}}^0} $,$ {{\boldsymbol{S}}^0} $为全零矩阵,$ k = 0 $ (4) While $ k < K $ do (5) $ {{\boldsymbol{G}}_{{{\text{1}}_k}}}{\text{ = }}\frac{1}{2}{{\boldsymbol{L}}^k} - \frac{1}{2}{{\boldsymbol{S}}^k} + \frac{1}{2}{\boldsymbol{R}} $ (6) $ {{\boldsymbol{G}}_{{{\text{2}}_k}}}{\text{ = }}\frac{1}{2}{{\boldsymbol{S}}^k} - \frac{1}{2}{{\boldsymbol{L}}^k} + \frac{1}{2}{\boldsymbol{R}} $ (7) $ {{\boldsymbol{L}}^{k + 1}} = {\text{SV}}{{\text{T}}_{{\lambda _1}/{L_f}}}\left\{ {{{\boldsymbol{G}}_{{{\text{1}}_k}}}} \right\} $ (8) $ {{\boldsymbol{S}}^{k + 1}} = {\mathcal{T}_{{\lambda _2}/{L_f}}}\left\{ {{{\boldsymbol{G}}_{{2_k}}}} \right\} $ (9) $ k \leftarrow k + 1 $ (10) end while (11) 输出$ {{\boldsymbol{L}}^K} $和$ {{\boldsymbol{S}}^K} $,并计算归一化均方误差NMSE (12) 执行会话 (13) for 隐藏层或输出层的每个神经元 do (14) 更新网络中的每一个权值和偏差 (15) end for (16) end for -
[1] 蒋俊正, 杨杰, 欧阳缮. 一种新的无线传感器网络中异常节点检测定位算法[J]. 电子与信息学报, 2018, 40(10): 2358–2364. doi: 10.11999/JEIT171207JIANG Junzheng, YANG Jie, and OUYANG Shan. Novel method for outlier nodes detection and localization in wireless sensor networks[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2358–2364. doi: 10.11999/JEIT171207 [2] 郭志懋, 周傲英. 数据质量和数据清洗研究综述[J]. 软件学报, 2002, 13(11): 2076–2082.GUO Zhimao and ZHOU Aoying. Research on data quality and data cleaning: A survey[J]. Journal of Software, 2002, 13(11): 2076–2082. [3] YU Tianqi, WANG Xianbin, and SHAMI A. Recursive principal component analysis-based data outlier detection and sensor data aggregation in IoT systems[J]. IEEE Internet of Things Journal, 2017, 4(6): 2207–2216. doi: 10.1109/JIOT.2017.2756025 [4] KUMAR V and KHOSLA C. Data cleaning-a thorough analysis and survey on unstructured data[C]. The 8th International Conference on Cloud Computing, Data Science & Engineering, Noida, India, 2018: 305–309. [5] DIAO Yinglong, LIU Keyan, MENG Xiaoli, et al. A big data online cleaning algorithm based on dynamic outlier detection[C]. 2015 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Xi'an, China, 2015: 230–234. [6] 田江, 顾宏. 孤立点一类支持向量机算法研究[J]. 电子与信息学报, 2010, 32(6): 1284–1288. doi: 10.3724/SP.J.1146.2009.00861TIAN Jiang and GU Hong. Outlier one class support vector machines[J]. Journal of Electronics &Information Technology, 2010, 32(6): 1284–1288. doi: 10.3724/SP.J.1146.2009.00861 [7] ZOU Zhuping, XIE Yulai, HUANG Kai, et al. A docker container anomaly monitoring system based on optimized isolation forest[J]. IEEE Transactions on Cloud Computing, To be published. doi: 10.1109/TCC.2019.2935724. [8] ZHOU Zihan, LI Xiaodong, WRIGHT J, et al. Stable principal component pursuit[C]. 2010 IEEE International Symposium on Information Theory, Austin, USA, 2010: 1518–1522. [9] XU Yichu, DU Bo, ZHANG Liangpei, et al. A low-rank and sparse matrix decomposition-based dictionary reconstruction and anomaly extraction framework for hyperspectral anomaly detection[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(7): 1248–1252. doi: 10.1109/LGRS.2019.2943861 [10] DAUBECHIES I, DEFRISE M, and DE MOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413–1457. doi: 10.1002/cpa.20042 [11] BIOUCAS-DIAS J M and FIGUEIREDO M A T. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration[J]. IEEE Transactions on Image Processing, 2007, 16(12): 2992–3004. doi: 10.1109/TIP.2007.909319 [12] CANDES E J, WAKIN M B, and BOYD S. Enhancing sparsity by reweighted l1 minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877–905. [13] ELAD M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing[M]. New York: Springer, 2010: 185–200. [14] CHENG Jie, YE Qiang, JIANG Hongbo, et al. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(2): 850–861. doi: 10.1109/TWC.2012.121412.120148 [15] 李鹏, 王建新, 曹建农. 无线传感器网络中基于压缩感知和GM(1, 1)的异常检测方案[J]. 电子与信息学报, 2015, 37(7): 1586–1590. doi: 10.11999/JEIT141219LI Peng, WANG Jianxin, and CAO Jiannong. Abnormal event detection scheme based on compressive sensing and GM (1, 1) in wireless sensor networks[J]. Journal of Electronics &Information Technology, 2015, 37(7): 1586–1590. doi: 10.11999/JEIT141219 [16] LIU Jing and RAO B D. Robust PCA via ℓ0-ℓ1 regularization[J]. IEEE Transactions on Signal Processing, 2019, 67(2): 535–549. doi: 10.1109/TSP.2018.2883924 [17] RAHMANI M and ATIA G K. High dimensional low rank plus sparse matrix decomposition[J]. IEEE Transactions on Signal Processing, 2017, 65(8): 2004–2019. doi: 10.1109/TSP.2017.2649482 [18] ORTIZ-RODRIGUEZ J M and VEGA-CARRILLO H R. A neutron spectra unfolding code, based on iterative procedures, designed under LabVIEW environment[C]. 2012 IEEE Ninth Electronics, Robotics and Automotive Mechanics Conference, Cuernavaca, Mexico, 2012: 315–319. [19] GIRYES R, ELDAR Y C, BRONSTEIN A M, et al. Tradeoffs between convergence speed and reconstruction accuracy in inverse problems[J]. IEEE Transactions on Signal Processing, 2018, 66(7): 1676–1690. doi: 10.1109/TSP.2018.2791945 [20] YANG Yang, SUN Jian, LI Huibin, et al. ADMM-CSNet: A deep learning approach for image compressive sensing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(3): 521–538. doi: 10.1109/TPAMI.2018.2883941 [21] CHEN Yunjin, WEI Yu, and POCK T. On learning optimized reaction diffusion processes for effective image restoration[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 5261–5269. [22] SOLOMON O, COHEN R, ZHANG Yi, et al. Deep unfolded robust PCA with application to clutter suppression in ultrasound[J]. IEEE Transactions on Medical Imaging, 2020, 39(4): 1051–1063. doi: 10.1109/TMI.2019.2941271 [23] Intel Berkeley Research Lab. Intel lab data[EB/OL]. http://db.lcs.mit.edu/labdata/labdata.html, 2019. [24] 苏凤阁. 大纳伦河流域修正后的温度和降水数据集(1951–2016)[R]. 国家青藏高原科学数据中心, 2019. doi: 10.11888/Hydro.tpdc.270216.SU Fengge. Revised dataset of temperature and precipitation in the Greater Naren River Basin (1951–2016)[R]. National Tibetan Plateau Data Center, 2019. doi: 10.11888/Hydro.tpdc.270216. -





 下载:
下载:



 下载:
下载:
