Underwater Target Depth Classification Method Based on Vertical Acoustic Intensity Flux
-
摘要: 现有的基于声场干涉结构特征的目标深度分类方法的频率适用范围有限,仅适用于目标线谱频率激发前2阶简正波的情况。针对上述问题,该文提出基于匹配场处理的目标深度分类算法,该算法将垂直复声强无功分量作为匹配量进行目标深度的匹配估计,利用目标深度的粗略估计结果辅助进行目标深度的二元分类。算法适用于线谱频率激发前3阶简正波的情况,有效拓展了算法的频率适用范围。仿真结果验证了算法的可行性和稳健性。该文分析了环境失配情况对算法性能的影响。所提算法具有较高的准确性和稳健性。Abstract: The existing target depth classification methods based on acoustic interference structure characteristics have a limited frequency range, and are only suitable for the case where target frequency can excite first two modes. Aiming to this problem, a novel target depth classification algorithm based on matching field processing is proposed in this paper. The proposed algorithm uses the reactive component of vertical complex acoustic intensity as matching variable to estimate target depth. The rough estimation results of target depth can be used to assist the binary classification of target depth. This method is suitable for the case where target frequency can excite first three modes, so as to expand the frequency range of the algorithm. The feasibility and robustness of the algorithm are verified by simulation results. The influence of mismatched sea environmental parameters on algorithm performance are also analyzed. The proposed algorithm has high accuracy and robustness.
-
表 1 本文算法与现有算法的性能对比
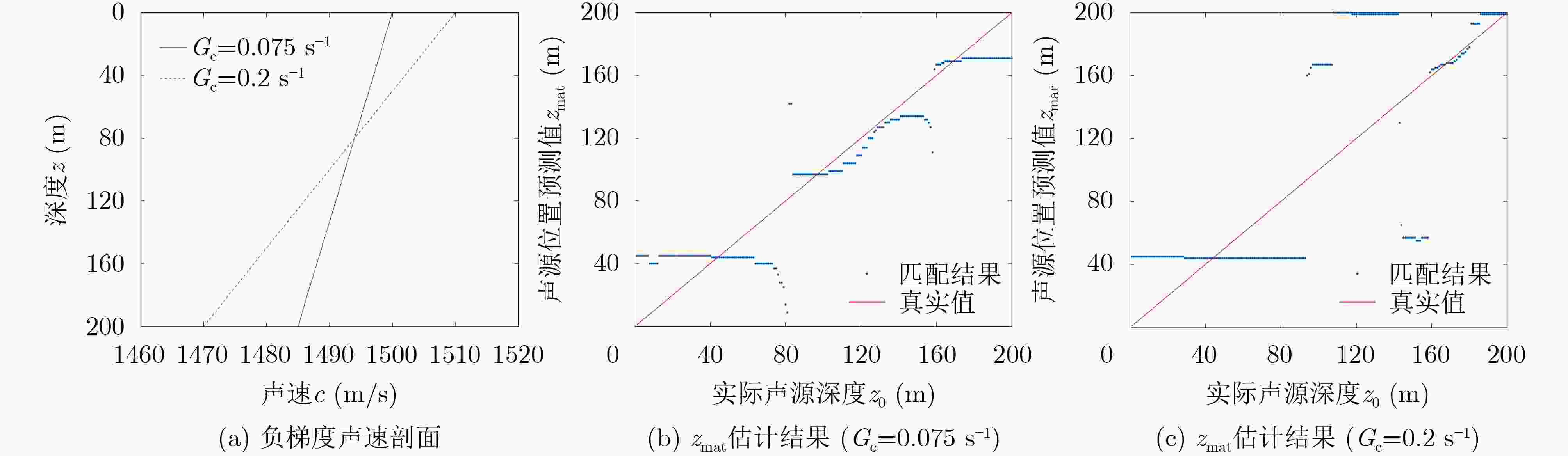
本文算法 现有算法1 现有算法2 现有算法3 现有算法4 现有算法5 目标数目要求 单一目标 单一目标 单一目标 单一目标 单一目标 单一目标 阵元数目要求 单阵元 垂直阵 双阵元 单阵元 垂直阵 单阵元 信噪比要求 ${\rm{SNR }}\ge - 20\;{\rm{ dB} }$ 未分析 未分析 较高(爆炸源) 未分析 较高(气枪) 目标频率适用范围 低频窄带(存在3阶简正波) 低频宽带 低频窄带(存在两阶简正波) 低频宽带 低频窄带 低频宽带 声速分布适用性 弱负梯度
强温跃层弱温跃层 弱负梯度
弱温跃层等声速
弱负梯度无限制 等声速
弱负梯度 -
[1] EMMETIÈRE R, BONNEL J, CRISTOL X, et al. Passive source depth discrimination in deep-water[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(1): 185–197. doi: 10.1109/JSTSP.2019.2899968 [2] CHO S I, KIM D, and KIM J S. Source depth discrimination based on channel impulse response[J]. The Journal of the Acoustical Society of Korea, 2019, 38(1): 120–127. [3] YU Yun, LING Qing, and XU Jiang. Pressure and velocity cross-spectrum of normal modes in low-frequency acoustic vector field of shallow water and its application[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 241–249. doi: 10.1109/JSEE.2015.00029 [4] 刘志韬, 郭良浩, 闫超. 利用自相关函数warping变换的浅海声源深度判别[J]. 声学学报, 2019, 44(1): 28–38.LIU Zhitao, GUO Lianghao, and YAN Chao. Source depth discrimination in shallow water based on relation formula warping transform[J]. Acta Acustica, 2019, 44(1): 28–38. [5] HAN Ning and YAO Shuai. Discrimination of the active submerged/bottom target based on the total scintillation index[J]. Applied Acoustics, 2021, 172: 107646. doi: 10.1016/j.apacoust.2020.107646 [6] LI Hui, YANG Kunde, DUAN Rui, et al. Joint estimation of source range and depth using a bottom-deployed vertical line array in deep water[J]. Sensors, 2017, 17(6): 1315. doi: 10.3390/s17061315 [7] 王森, 王余, 王易川, 等. 水下高速目标声谱图特征提取及分类设计[J]. 电子与信息学报, 2017, 39(11): 2684–2689.WANG Sen, WANG Yu, WANG Yichuan, et al. Feature extraction and classification of spectrum of radiated noise of underwater high speed vehicle[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2684–2689. [8] YANG T C. Source localization in range-dependent and time-varying shallow water: The Shallow Water 2006 experimental results[J]. The Journal of the Acoustical Society of America, 2019, 146(6): 4740–4753. doi: 10.1121/1.5138595 [9] 李焜, 方世良, 安良. 非合作水声脉冲信号的单水听器匹配场定位研究[J]. 电子与信息学报, 2012, 34(11): 2541–2547.LI Kun, FANG Shiliang, and AN Liang. Matched field localization for non-cooperative underwater acoustic pulse signals using a single hydrophone[J]. Journal of Electronics &Information Technology, 2012, 34(11): 2541–2547. [10] LEI Zhixiong, YANG Kunde, and MA Yuanliang. Passive localization in the deep ocean based on cross-correlation function matching[J]. The Journal of the Acoustical Society of America, 2016, 139(6): EL196–EL201. doi: 10.1121/1.4954053 [11] 郭晓乐, 杨坤德, 马远良, 等. 一种基于简正波模态消频散变换的声源距离深度估计方法[J]. 物理学报, 2016, 65(21): 214302. doi: 10.7498/aps.65.214302GUO Xiaole, YANG Kunde, MA Yuanliang, et al. A source range and depth estimation method based on modal dedispersion transform[J]. Acta Physica Sinica, 2016, 65(21): 214302. doi: 10.7498/aps.65.214302 [12] DUAN Rui, YANG Kunde, LI Hui, et al. A performance study of acoustic interference structure applications on source depth estimation in deep water[J]. The Journal of the Acoustical Society of America, 2019, 145(2): 903–916. doi: 10.1121/1.5091100 [13] LIU Wenxu, YANG Yixin, LÜ Liangang, et al. Source localization by matching sound intensity with a vertical array in the deep ocean[J]. The Journal of the Acoustical Society of America, 2019, 146(6): EL477–EL481. doi: 10.1121/1.5139191 [14] 高飞, 孙磊. 基于首达波与次达波到达时差的深海浅层移动声源定位[J]. 兵工学报, 2018, 39(11): 2243–2248. doi: 10.3969/j.issn.1000-1093.2018.11.019GAO Fei and SUN Lei. Localization of moving acoustic source in shallow layer of deep ocean based on the time difference of arrival between the first and second waves[J]. Acta Armamentarii, 2018, 39(11): 2243–2248. doi: 10.3969/j.issn.1000-1093.2018.11.019 [15] 郑胜家, 韩东, 李晓, 等. 匹配场定位强干扰抑制最小方差无畸变响应处理技术[J]. 仪器仪表学报, 2014, 35(7): 1586–1593.ZHENG Shengjia, HAN Dong, LI Xiao, et al. Processor of minimum variance distortionless response with strong interference suppression for matched field processing[J]. Chinese Journal of Scientific Instrument, 2014, 35(7): 1586–1593. [16] 吴国清, 李靖, 陈耀明, 等. 舰船噪声识别(Ⅱ)——线谱稳定性和唯一性[J]. 声学学报, 1999, 24(1): 6–11.WU Guoqing, LI Jing, CHEN Yaoming, et al. Ship radiated-noise recognition(II)—stability and uniqueness of line spectrum[J]. Acta Acustica, 1999, 24(1): 6–11. -





 下载:
下载:


 下载:
下载:
