基于非对称监督深度离散哈希的图像检索

顾广华; 霍文华; 苏明月; 付灏

doi:10.11999/JEIT200988

基于非对称监督深度离散哈希的图像检索

doi: 10.11999/JEIT200988

1.
燕山大学信息科学与工程学院秦皇岛 066000
2.
河北省信息传输与信号处理重点实验室秦皇岛 066000

基金项目: 国家自然科学基金(62072394)，河北省自然科学基金(F2021203019)

详细信息

作者简介:
顾广华：男，1979年生，博士，教授，研究方向为图像检索、图像分类和图像识别

霍文华：女，1995年生，硕士生，研究方向为图像检索和深度哈希

苏明月：女，1996年生，硕士生，研究方向为图像检索和深度哈希

付灏：男，1996年生，硕士生，研究方向为跨模态检索

通讯作者:
顾广华　guguanghua@ysu.edu.cn

中图分类号: TN911.73; TP391.4
计量
- 文章访问数: 760
- HTML全文浏览量: 745
- PDF下载量: 79
- 被引次数: 0
出版历程
- 收稿日期: 2020-11-23
- 修回日期: 2021-10-25
- 录用日期: 2021-11-05
- 网络出版日期: 2021-11-09
- 刊出日期: 2021-12-21

Asymmetric Supervised Deep Discrete Hashing Based Image Retrieval

1.
School of Information Science and Engineering, Yanshan Engineering University, Qinhuangdao 066000, China
2.
Hebei Key Laboratory of Information Transmission and Signal Processing, Qinhuangdao 066000, China

Funds: The National Natural Science Foundation of China (62072394), The Natural Science Foundation of Hebei Province (F2021203019)

摘要

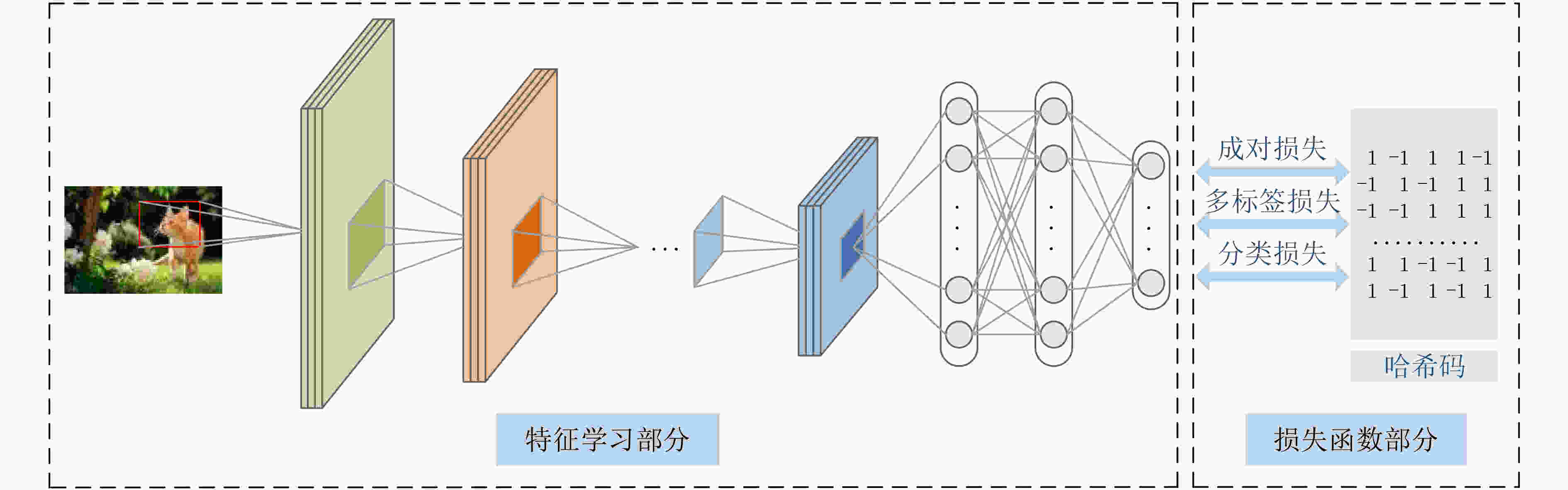
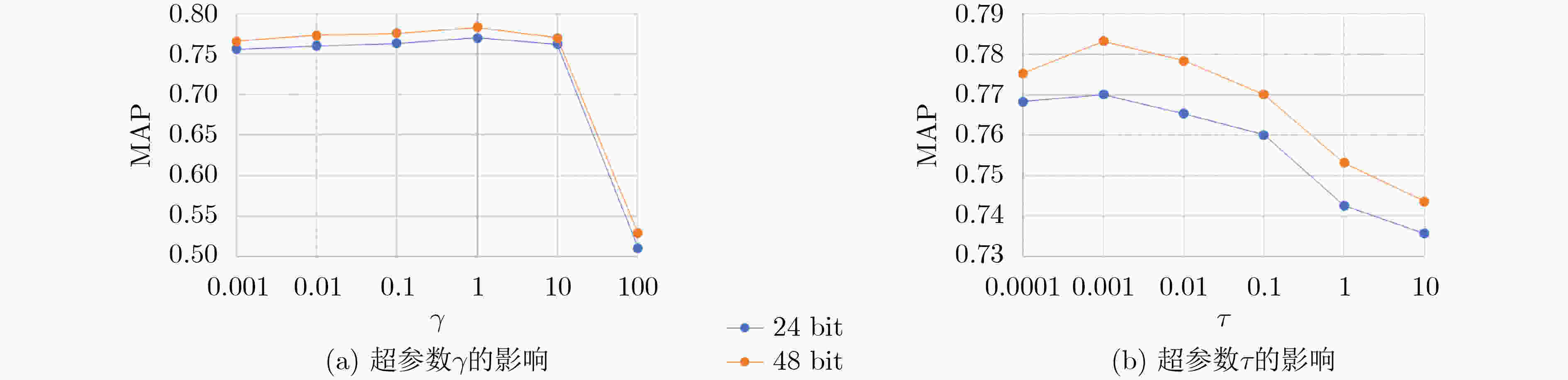
摘要: 哈希广泛应用于图像检索任务。针对现有深度监督哈希方法的局限性，该文提出了一种新的非对称监督深度离散哈希(ASDDH)方法来保持不同类别之间的语义结构，同时生成二进制码。首先利用深度网络提取图像特征，根据图像的语义标签来揭示每对图像之间的相似性。为了增强二进制码之间的相似性，并保证多标签语义保持，该文设计了一种非对称哈希方法，并利用多标签二进制码映射，使哈希码具有多标签语义信息。此外，引入二进制码的位平衡性对每个位进行平衡，鼓励所有训练样本中的–1和+1的数目近似。在两个常用数据集上的实验结果表明，该方法在图像检索方面的性能优于其他方法。
- 图像检索 /
- 监督哈希 /
- 语义保持 /
- 深度学习
Abstract: Hashing is widely used for image retrieval tasks. In view of the limitations of existing deep supervised hashing methods, a new Asymmetric Supervised Deep Discrete Hashing (ASDDH) method is proposed to maintain the semantic structure between different categories and generate binary codes. Firstly, a deep network is used to extract image features and reveal the similarity between each pair of images according to their semantic labels. To enhance the similarity between binary codes and ensure the retention of multi-label semantics, this paper designs an asymmetric hashing method that utilizes a multi-label binary code mapping to make the hash codes have multi-label semantic information. In addition, the bit balance of the binary code is introduced to balance each bit, which encourages the number of -1 and +1 to be approximately similar among all training samples. Experimental results on two benchmark datasets show that the proposed method is superior to other methods in image retrieval.
- Image retrieval /
- Supervised hashing /
- Semantic preservation /
- Deep learning

HTML全文

图 1 ASDDH模型体系结构

下载: 全尺寸图片幻灯片

图 2 CIFAR-10数据集上的超参数影响

下载: 全尺寸图片幻灯片

表 1 两个数据集上不同方法的MAP

方法	CIFAR-10 (bit)				NUS-WIDE (bit)
方法	12	24	32	48	12	24	32	48
ASDDH	0.763	0.771	0.781	0.785	0.834	0.851	0.868	0.874
DSDH*^[14]	0.723	0.734	0.749	0.751	0.763	0.780	0.784	0.801
DPSH^[13]	0.713	0.727	0.744	0.757	0.752	0.790	0.794	0.812
DTSH^[27]	0.710	0.750	0.765	0.774	0.773	0.808	0.812	0.824
DQN^[23]	0.554	0.558	0.564	0.580	0.768	0.776	0.783	0.792
DHN^[24]	0.555	0.594	0.603	0.621	0.708	0.735	0.748	0.758
NINH^[26]	0.552	0.566	0.558	0.581	0.674	0.697	0.713	0.715
CNNH^[25]	0.439	0.511	0.509	0.522	0.611	0.618	0.625	0.608
FastH+CNN^[21]	0.553	0.607	0.619	0.636	0.779	0.807	0.816	0.825
SDH+CNN^[10]	0.478	0.557	0.584	0.592	0.780	0.804	0.815	0.824
KSH+CNN^[9]	0.488	0.539	0.548	0.563	0.768	0.786	0.790	0.799
LFH+CNN^[22]	0.208	0.242	0.266	0.339	0.695	0.734	0.739	0.759
SPLH+CNN^[20]	0.299	0.330	0.335	0.330	0.753	0.775	0.783	0.786
ITQ+CNN^[5]	0.237	0.246	0.255	0.261	0.719	0.739	0.747	0.756
SH+CNN^[19]	0.183	0.164	0.161	0.161	0.621	0.616	0.615	0.612

下载: 导出CSV

表 2 不同网络的MAP

方法	CIFAR-10 (bit)
方法	12	24	36	48
ASDDH	0.763	0.771	0.781	0.785
ASDDH-V16	0.783	0.792	0.798	0.810
ASDDH-RN50	0.794	0.803	0.810	0.822
ASDDH-RNX50	0.810	0.827	0.839	0.841
DSDH	0.723	0.734	0.749	0.751
DSDH-V16	0.741	0.752	0.763	0.774
DSDH--RN50	0.755	0.767	0.770	0.786
DSDH-RNX50	0.781	0.792	0.794	0.798

下载: 导出CSV

参考文献(27)

[1]	SHEN Fumin, ZHOU Xiang, YANG Yang, et al. A fast optimization method for general binary code learning[J]. IEEE Transactions on Image Processing, 2016, 25(12): 5610–5621. doi: 10.1109/TIP.2016.2612883
[2]	QIANG Haopeng, WAN Yuan, XIANG Lun, et al. Deep semantic similarity adversarial hashing for cross-modal retrieval[J]. Neurocomputing, 2020, 400: 24–33. doi: 10.1016/j.neucom.2020.03.032
[3]	彭天强, 栗芳. 基于深度卷积神经网络和二进制哈希学习的图像检索方法[J]. 电子与信息学报, 2016, 38(8): 2068–2075. doi: 10.11999/JEIT151346 PENG Tianqiang and LI Fang. Image retrieval based on deep convolutional neural networks and binary hashing learning[J]. Journal of Electronics &Information Technology, 2016, 38(8): 2068–2075. doi: 10.11999/JEIT151346
[4]	DATAR M, IMMORLICA N, INDYK P, et al Locality-sensitive hashing scheme based on p-stable distributions[C]. Proceedings of the 20th Annual Symposium on Computational Geometry, New York, USA, 2004: 253–262. doi: 10.1145/997817.997857.
[5]	GONG Yunchao and LAZEBNIK S. Iterative quantization: A procrustean approach to learning binary codes[C]. Proceedings of CVPR 2011, Colorado Springs, USA, 2011: 817–824. doi: 10.1109/CVPR.2011.5995432.
[6]	LIU Wei, MU Cun, SANJIV K, et al. Discrete graph hashing[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 3419–3427.
[7]	LU Xiaoqiang, ZHENG Xiangtao, and LI Xuelong. Latent semantic minimal hashing for image retrieval[J]. IEEE Transactions on Image Processing, 2017, 26(1): 355–368. doi: 10.1109/TIP.2016.2627801
[8]	DAI Bo, GUO Ruiqi, KUMAR S, et al. Stochastic generative hashing[C]. Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017: 913–922.
[9]	LIU Wei, WANG Jun, JI Rongrong, et al. Supervised hashing with kernels[C]. Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, USA, 2012: 2074–2081. doi: 10.1109/CVPR.2012.6247912.
[10]	SHEN Fumin, SHEN Chunhua, LIU Wei, et al. Supervised discrete hashing[C]. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 37–45. doi: 10.1109/CVPR.2015.7298598.
[11]	SHI Xiaoshuang, XING Fuyong, XU Kaidi, et al. Asymmetric discrete graph hashing[C]. Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, USA, 2017: 2541–2547.
[12]	陈昌红, 彭腾飞, 干宗良. 基于深度哈希算法的极光图像分类与检索方法[J]. 电子与信息学报, 2020, 42(12): 3029–3036. doi: 10.11999/JEIT190984 CHEN Changhong, PENG Tengfei, and GAN Zongliang. Aurora image classification and retrieval method based on deep hashing algorithm[J]. Journal of Electronics &Information Technology, 2020, 42(12): 3029–3036. doi: 10.11999/JEIT190984
[13]	LI Wujun, WANG Sheng, and KANG Wangcheng. Feature learning based deep supervised hashing with pairwise labels[C]. Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, USA, 2016: 1711–1717.
[14]	GUI Jie, LIU Tongliang, SUN Zhenan, et al. Fast supervised discrete hashing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(2): 490–496. doi: 10.1109/TPAMI.2017.2678475
[15]	JIANG Qingyuan, CUI Xue, and LI Wujun. Deep discrete supervised hashing[J]. IEEE Transactions on Image Processing, 2018, 27(12): 5996–6009. doi: 10.1109/TIP.2018.2864894
[16]	MA Lei, LI Hongliang, WU Qingbo, et al. Multi-task learning for deep semantic hashing[C]. Proceedings of 2018 IEEE Visual Communications and Image Processing, Taichung, China, 2018: 1–4. doi: 10.1109/VCIP.2018.8698627.
[17]	YANG Zhan, RAYMOND O I, SUN Wuqing, et al. Asymmetric deep semantic quantization for image retrieval[J]. IEEE Access, 2019, 7: 72684–72695. doi: 10.1109/ACCESS.2019.2920712
[18]	MOHAMMAD N and FLEET D J. Minimal loss hashing for compact binary codes[C]. Proceedings of the 28th International Conference on Machine Learning, Bellevue, USA, 2011: 353–360.
[19]	WEISS Y, TORRALBA A, and FERGUS R. Spectral hashing[C]. Proceedings of the 21st International Conference on Neural Information Processing Systems, Vancouver, Canada, 2008: 1753–1760. doi: 10.5555/2981780.2981999.
[20]	WANG Jun, KUMAR S, and CHANG S F. Sequential projection learning for hashing with compact codes[C]. Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 2010: 1127–1134.
[21]	LIN Guosheng, SHEN Chunhua, SHI Qinfeng, et al. Fast supervised hashing with decision trees for high-dimensional data[C]. Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, USA, 2014: 1971–1978. doi: 10.1109/CVPR.2014.253.
[22]	ZHANG Peichao, ZHANG Wei, LI Wujun, et al. Supervised hashing with latent factor models[C]. Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval, Gold Coast, Australia, 2014: 173–182. doi: 10.1145/2600428.2609600.
[23]	CAO Yue, LONG Mingsheng, WANG Jianmin, et al. Deep quantization network for efficient image retrieval[C]. Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, USA, 2016: 3457–3463.
[24]	ZHU Han, LONG Mingsheng, WANG Jianmin, et al. Deep hashing network for efficient similarity retrieval[C]. Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, USA, 2016: 2415–2421.
[25]	XIA Rongkai, PAN Yan, LAI Hanjiang, et al. Supervised hashing for image retrieval via image representation learning[C]. Proceedings of the 28th AAAI Conference on Artificial Intelligence, Québec City, Canada, 2014: 2156–2162.
[26]	LAI Hanjiang, PAN Yan, LIU Ye, et al. Simultaneous feature learning and hash coding with deep neural networks[C]. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 3270–3278. doi: 10.1109/CVPR.2015.7298947.
[27]	WANG Xiaofang, SHI Yi, and KITANI K M. Deep supervised hashing with triplet labels[C]. Proceedings of the 13th Asian Conference on Computer Vision, Taipei, China, 2016: 70–84. doi: 10.1007/978-3-319-54181-5_5.