基于集合经验模态分解和信号结构分析的心电信号R波识别算法

林金朝; 李必禄; 李国权; 黄正文; 庞宇

doi:10.11999/JEIT200915

基于集合经验模态分解和信号结构分析的心电信号R波识别算法

doi: 10.11999/JEIT200915

林金朝^{1, 3},
李必禄^{1, 3},
李国权^{1, 3, ,},
黄正文²,
庞宇³

1.
重庆邮电大学通信与信息工程学院重庆 400065
2.
布鲁内尔大学电子与计算机工程系伦敦 UB8 3PH
3.
光电信息感测与传输技术重点实验室重庆 400065

基金项目: 国家重点研发计划(2019YFC1511300)，国家自然科学基金(61971079)，重庆市自然科学基金面上项目(cstc2019jcyj-msxmX0666)，四川省区域创新合作项目(2020YFQ0025)，重庆市创新群体(cstc2020jcyj-cxttX0002)，重庆市教委科学技术研究项目(KJZD-K20200604)

详细信息

作者简介:
林金朝：男，1966年生，教授，研究方向为无线通信传输技术、医疗信号处理等

李必禄：男，1997年生，硕士，研究方向为医疗信号处理、人工智能

李国权：男，1980年生，教授，研究方向为MIMO无线通信传输技术、医疗信号处理等

黄正文：男，1981年生，讲师/高级研究员，研究方向为人工智能、复杂系统优化、数据分析等

庞宇：男，1978年生，讲师，博士生导师，研究方向为无线通信、集成电路设计、数字医疗研究以及人工智能

通讯作者:
李国权　ligq@cqupt.edu.cn

中图分类号: TN911.72; R540.41
计量
- 文章访问数: 710
- HTML全文浏览量: 405
- PDF下载量: 76
- 被引次数: 0
出版历程
- 收稿日期: 2020-10-26
- 修回日期: 2021-07-21
- 网络出版日期: 2021-07-22
- 刊出日期: 2021-08-10

ElectroCardioGram R-wave Recognition Algorithm Based on Ensemble Empirical Mode Decomposition and Signal Structure Analysis

Jinzhao LIN^{1, 3},
Bilu LI^{1, 3},
Guoquan LI^{1, 3
, ,},
Zhengwen HUANG²,
Yu PANG³

1.
School of Communication and Information Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
Department of Electronic and Computer Engineering, Brunel University London, London UB8-3PH, UK
3.
Key Laboratory of Photoelectric Information Sensing and Transmission Technology, Chongqing 400065, China

Funds: The National Key Research and Development Program (2019yfc1511300), The National Natural Science Foundation of China (61971079)，The General Program of Chongqing Natural Science Foundation (cstc2019jcyj-msxmx0666), The Sichuan Innovation Cooperation Program (2020YFQ0025), The Chongqing Creative Group Program (cstc2020jcyj-cxttX0002), The Science and Technology Research Program of Chongqing Education Committee (KJZD-K20200604)

摘要

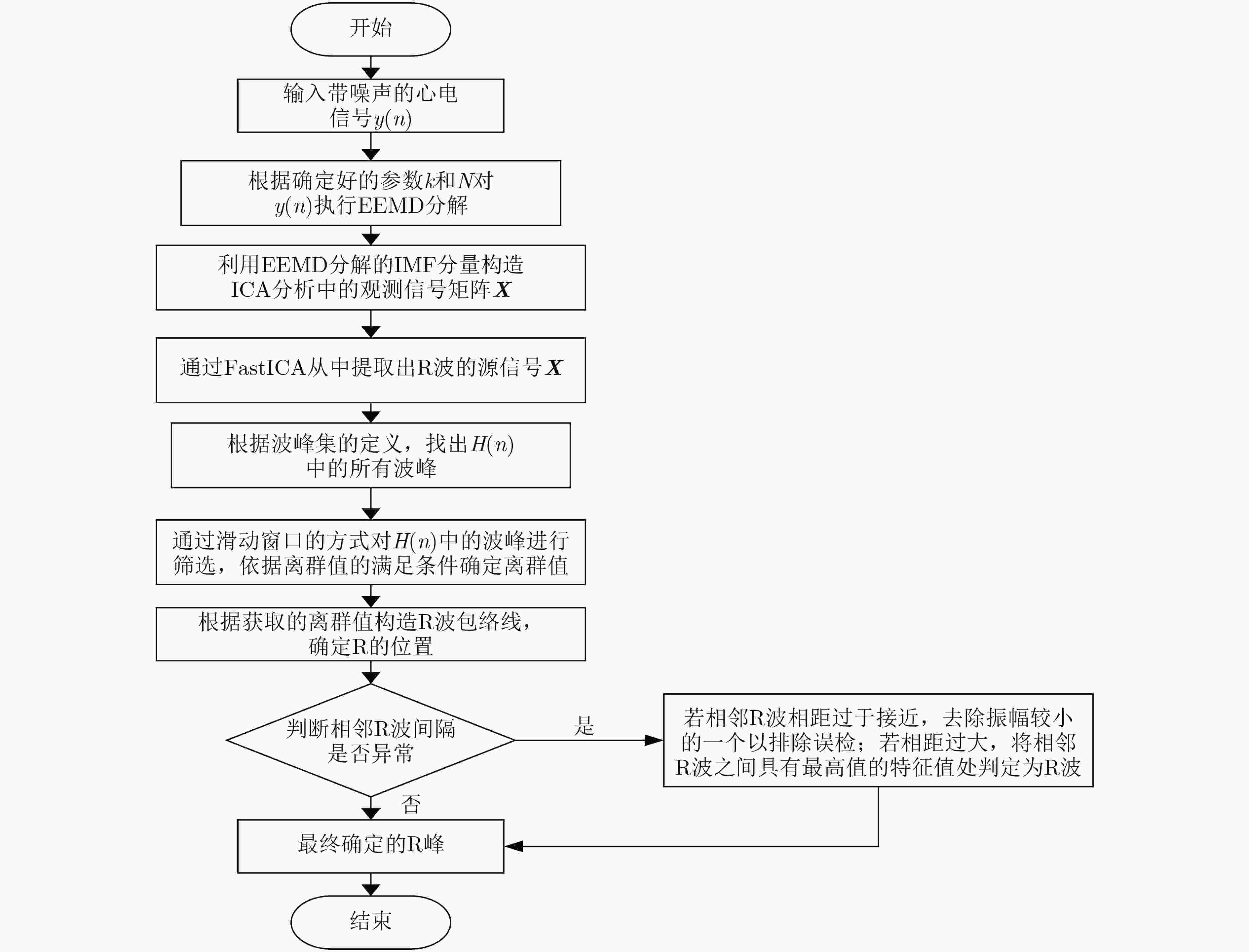
摘要: R波作为确定心电信号各波段的重要参考，是心电自动分析的前提。针对大多数R波识别算法的预处理过程影响识别准确度和耗时问题，该文提出一种基于集合经验模态分解(EEMD)和信号结构分析的算法对带噪心电信号(ECG)的R波直接进行识别。首先通过EEMD将带噪声的心电信号分解成一系列本征模态分量，然后对分解后的各模态分量作独立成分分析以提取出R波特征最明显的成分，对该成分进行结构分析，从而实现对R波的准确定位。仿真结果表明，该文算法对带噪声心电信号的R波识别具有更优性能，对异常心电信号的R波识别也具有明显效果。
- 心电信号 /
- R波识别 /
- 集合经验模态分解 /
- 信号结构分析
Abstract: In view of the problem that the preprocessing process of most R-wave recognition algorithms affects the accuracy of recognition and spends more time, an algorithm based on Ensemble Empirical Mode Decomposition (EEMD) and signal structure analysis is proposed to recognize R-wave of ElectroCardioGram (ECG) signals with noise directly. Firstly, the ECG signal with noise is decomposed into a series of intrinsic mode components by EEMD. After that, the intrinsic components are analyzed as independent components to extract the most obvious component of R waves. Finally, the structure of the component is analyzed to realize the accurate positioning of R wave. The simulation results show that the proposed algorithm has better performance in R-wave recognition of noisy ECG signals and demonstrates obvious advantages especially for abnormal ECG signals.
- ElectroCardioGraphy (ECG) /
- R-wave recognition /
- Ensemble Empirical Mode Decomposition (EEMD) /
- Signal structure analysis

HTML全文

图 1 本文算法流程图

下载: 全尺寸图片幻灯片

图 2 原始sel223信号和添加5 dB高斯白噪声的sel223信号

下载: 全尺寸图片幻灯片

图 3 Pan-Tomkins算法对$y(n)$的R波检测结果

下载: 全尺寸图片幻灯片

图 4 EEMD-ICA算法对$y(n)$的R波检测结果

下载: 全尺寸图片幻灯片

图 5 本文算法对$y(n)$的R波检测结果

下载: 全尺寸图片幻灯片

图 6 长停顿心电信号片段R波识别效果

下载: 全尺寸图片幻灯片

图 7 T波高大心电信号片段R波识别效果

下载: 全尺寸图片幻灯片

表 1 本文算法R波识别性能评估

ECG记录	R峰总数	漏检	误检	错检总数	灵敏度(%)	阳性准确率(%)	准确率(%)
sel100	1134	0	3	3	100.00	99.74	99.74
sel103	1048	0	0	0	100.00	100.00	100.00
sel116	1185	0	0	0	100.00	100.00	100.00
sel213	1642	0	1	1	100.00	99.94	99.94
sel221	1247	1	4	5	99.92	99.68	99.60
sel223	1309	3	2	5	99.77	99.85	99.62
sel230	1077	0	0	0	100.00	100.00	100.00
sel301	1351	2	0	2	99.85	100.00	99.85
sel310	2012	3	0	3	99.85	100.00	99.85
sel803	1026	0	0	0	100.00	100.00	100.00
sel853	1113	1	0	1	99.91	100.00	99.91
sel891	1267	0	0	0	100.00	100.00	100.00
合计	15411	10	10	20	99.94	99.94	99.87

下载: 导出CSV

表 2 3种R波识别算法性能对比

R波识别算法	R波总数	漏检	误检	错检总数	灵敏度(%)	阳性准确率(%)	准确率(%)	平均处理时间(s)
Pan-Tomkins算法^[4]	15411	95	25	120	99.38	99.84	99.22	1.7194
EEMD-ICA算法^[17]	15411	144	40	184	99.07	99.74	98.81	76.9896
本文算法	15411	10	10	20	99.94	99.94	99.87	76.9335
带预处理算法^[26]	15411	13	140	153	99.91	99.09	99.02	114.607

下载: 导出CSV

参考文献(28)

[1]	HE Runnan, WANG Kuanquan, LI Qince, et al. A novel method for the detection of R-peaks in ECG based on K-Nearest Neighbors and Particle Swarm Optimization[J]. EURASIP Journal on Advances in Signal Processing, 2017, 2017(1): 82. doi: 10.1186/s13634-017-0519-3
[2]	KULKARNI S S and RAJANKAR S O. Preprocessing techniques of electrocardiogram[J]. International Journal of Engineering and Computer Science, 2016, 5(6): 16746–16748.
[3]	ZALABARRIA U, IRIGOYEN E, MARTINEZ R, et al. Online robust R-peaks detection in noisy electrocardiograms using a novel iterative smart processing algorithm[J]. Applied Mathematics and Computation, 2020, 369: 124839. doi: 10.1016/j.amc.2019.124839
[4]	赵崇侃. 双时值QRS波检出电路[J]. 中国医疗器械杂志, 1995(3): 158–160. ZHAO Chongkan. A circuit for detecting QRS wave with dual time constant[J]. Chinese Journal of Medical Instrumentation, 1995(3): 158–160.
[5]	PAN Jiapu and TOMPKINS W J. A real-time QRS detection algorithm[J]. IEEE Transactions on Biomedical Engineering, 1985, BME-32(3): 230–236. doi: 10.1109/TBME.1985.325532
[6]	NAYAK C, SAHA S K, KAR R, et al. An efficient QRS complex detection using optimally designed digital differentiator[J]. Circuits, Systems, and Signal Processing, 2019, 38(2): 716–749. doi: 10.1007/s00034-018-0880-y
[7]	PARK J S, LEE S W, and PARK U. R peak detection method using wavelet transform and modified Shannon energy envelope[J]. Journal of Healthcare Engineering, 2017, 2017: 4901017. doi: 10.1155/2017/4901017
[8]	吴建, 李康, 庞宇, 等. 基于差分阈值与模板匹配的心电R波提取算法[J]. 重庆邮电大学学报: 自然科学版, 2015, 27(3): 372–376. doi: 10.3979/j.issn.1673-825X.2015.03.014 WU Jian, LI Kang, PANG Yu, et al. Algorithm of ECG R-wave extraction based on differential threshold and template matching[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2015, 27(3): 372–376. doi: 10.3979/j.issn.1673-825X.2015.03.014
[9]	MERAH M, ABDELMALIK T A, and LARBI B H. R-peaks detection based on stationary wavelet transform[J]. Computer Methods and Programs in Biomedicine, 2015, 121(3): 149–160. doi: 10.1016/j.cmpb.2015.06.003
[10]	孙亚楠, 吕可嘉, 张瑞. 一种新的心电信号R峰自动检测方法[J]. 西北大学学报: 自然科学版, 2018, 48(1): 16–23. doi: 10.16152/j.cnki.xdxbzr.2018-01-004 SUN Yanan, LÜ Kejia, and ZHANG Rui. A novel automatic R peak detection method using ECG[J]. Journal of Northwest University:Natural Science Edition, 2018, 48(1): 16–23. doi: 10.16152/j.cnki.xdxbzr.2018-01-004
[11]	季虎, 孙即祥, 王春光. 基于小波变换的自适应QRS-T对消P波检测算法[J]. 电子与信息学报, 2007, 29(8): 1868–1871. doi: 10.3724/SP.J.1146.2006.00117 JI Hu, SUN Jixiang, and WANG Chunguang. An adaptive QRS-T cancellation based on wavelet transform for P-wave detection[J]. Journal of Electronics &Information Technology, 2007, 29(8): 1868–1871. doi: 10.3724/SP.J.1146.2006.00117
[12]	熊鹏, 刘学朋, 杜海曼, 等. 基于平稳和连续小波变换融合算法的心电信号P, T波检测[J]. 电子与信息学报, 2021, 43(5): 1441–1447. doi: 10.11999/JEIT200049 XIONG Peng, LIU Xuepeng, DU Haiman, et al. Detection of ECG signal P and T wave based on stationary and continuous wavelet transform fusion[J]. Journal of Electronics &Information Technology, 2021, 43(5): 1441–1447. doi: 10.11999/JEIT200049
[13]	FARASHI S. A multiresolution time-dependent entropy method for QRS complex detection[J]. Biomedical Signal Processing and Control, 2016, 24: 63–71. doi: 10.1016/j.bspc.2015.09.008
[14]	行鸿彦, 黄敏松. 基于Hilbert-Huang变换的QRS波检测算法研究[J]. 仪器仪表学报, 2009, 30(7): 1469–1475. doi: 10.3321/j.issn:0254-3087.2009.07.025 XING Hongyan and HUANG Minsong. Research on the QRS complex detection algorithm based on Hilbert-Huang transform[J]. Chinese Journal of Scientific Instrument, 2009, 30(7): 1469–1475. doi: 10.3321/j.issn:0254-3087.2009.07.025
[15]	GUTIÉRREZ-RIVAS R, GARCÍA J J, MARNANE W P, et al. Novel real-time low-complexity QRS complex detector based on adaptive thresholding[J]. IEEE Sensors Journal, 2015, 15(10): 6036–6043. doi: 10.1109/JSEN.2015.2450773
[16]	KAUR R and KUMAR A. Comparative analysis of various QRS techniques in ECG[J]. International Journal of Computer Science and Mobile Computing, 2016, 5(2): 68–75. doi: 10.1109/IJCSMC.2016.526875
[17]	ARBATENI K and BENNIA A. Sigmoidal radial basis function ANN for QRS complex detection[J]. Neurocomputing, 2014, 145: 438–450. doi: 10.1016/j.neucom.2014.05.009
[18]	DEV SHARMA L and SUNKARIA R K. A robust QRS detection using novel pre-processing techniques and kurtosis based enhanced efficiency[J]. Measurement, 2016, 87: 194–204. doi: 10.1016/j.measurement.2016.03.015
[19]	SAFARI A, HESAR H D, MOHEBBI M, et al. A novel method for R-peak detection in noisy ECG signals using EEMD and ICA[C]. The 23rd Iranian Conference on Biomedical Engineering and 2016 1st International Iranian Conference on Biomedical Engineering, Tehran, Iran, 2017: 155–158. doi: 10.1109/ICBME.2016.7890948.
[20]	WU Zhaohua and HUANG N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1–41. doi: 10.1142/S1793536909000047
[21]	陈略, 唐歌实, 訾艳阳, 等. 自适应EEMD方法在心电信号处理中的应用[J]. 数据采集与处理, 2011, 26(3): 361–366. doi: 10.3969/j.issn.1004-9037.2011.03.020 CHEN Lue, TANG Geshi, ZI Yanyang, et al. Application of adaptive ensemble empirical mode decomposition method to electrocardiogram signal processing[J]. Journal of Data Acquisition &Processing, 2011, 26(3): 361–366. doi: 10.3969/j.issn.1004-9037.2011.03.020
[22]	LI Yuan, ZHOU Zhuhuang, YUAN Yanchao, et al. An improved FastICA method for fetal ECG extraction[J]. Computational and Mathematical Methods in Medicine, 2018, 2018: 7061456. doi: 10.1155/2018/7061456
[23]	BURGUERA A. Fast QRS detection and ECG compression based on signal structural analysis[J]. IEEE Journal of Biomedical and Health Informatics, 2019, 23(1): 123–131. doi: 10.1109/JBHI.2018.2792404
[24]	LAGUNA P, MARK R G, GOLDBERG A, et al. A database for evaluation of algorithms for measurement of QT and other waveform intervals in the ECG[C]. The Computers in Cardiology 1997, Lund, Sweden, 1997: 673–676. doi: 10.1109/CIC.1997.648140.
[25]	QIN Q, LI JIANQING, YUE YINGGAO, et al. An adaptive and time-efficient ECG R-peak detection algorithm[J]. Journal of Healthcare Engineering, 2017, 2017: 5980541. doi: 10.1155/2017/5980541
[26]	KIM J and SHIN H. Simple and robust realtime QRS detection algorithm based on spatiotemporal characteristic of the QRS complex[J]. PLoS One, 2016, 11(3): e0150144. doi: 10.1371/journal.pone.0150144
[27]	REHMAN N and MANDIC D P. Multivariate empirical mode decomposition[J]. The Royal Society A: Mathematical, Physical and Engineering Sciences, 2010, 466(2117): 1291–1302. doi: 10.1098/rspa.2009.0502
[28]	UR REHMAN N and MANDIC D P. Filter bank property of multivariate empirical mode decomposition[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2421–2426. doi: 10.1109/TSP.2011.2106779