High-performance Hardware Architecture Design and Implementation of Ed25519 Algorithm
-
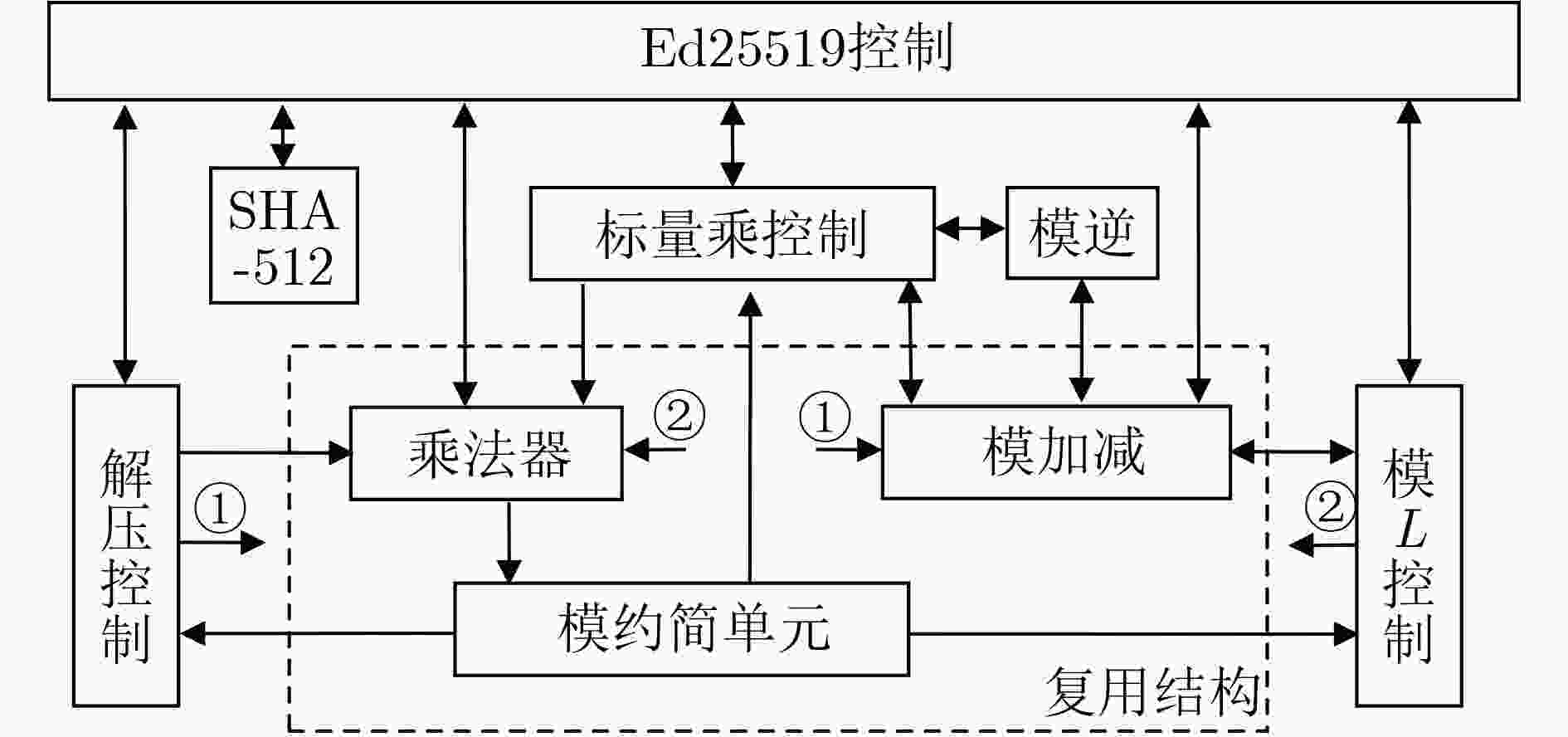
摘要: 针对签名验签速度难以满足特定应用领域需求的问题，该文设计了一种高性能Ed25519算法的硬件实现架构。采用宽度为2 bit的窗口法实现标量乘运算，减少了标量乘所需的总周期数；通过优化点加倍点操作步骤，提高了乘法器的硬件使用率；使用低计算复杂度的快速模约简实现模乘，提高了整体运算速度。为了使模L运算可复用标量乘中的快速模约简，该文提出一种基于Barrett约简的模L算法。通过优化解压过程中模幂操作过程，精简了步骤并使其可复用模乘。对所提架构做硬件实现，在TSMC的55 nm CMOS工艺下，面积为746×103等效门，最高频率360 MHz，每秒能够执行公钥生成9.06×104次、签名8.82×104次和验签3.99×104次。
-
关键词:
- 椭圆曲线数字签名算法 /
- 爱德华兹曲线 /
- 硬件实现 /
- 标量乘 /
- 快速模约简
Abstract: The speed of existing signature and verification architecture is difficult to meet the requirement of the specific applications domain, to solve this problem a high-performance hardware architecture of Ed25519 algorithm is developed. The scalar multiplication algorithm is implemented by using the window method with 2 bit width to reduce the total cycle numbers of the algorithm significantly. By optimizing the order of operations of point addition and point doubling, the hardware utilization rate of multiplier is improved. The module multiplication is realized by using fast module reduction with low computational complexity, thus the overall operation speed is improved. The modular L algorithm based on Barrett reduction is proposed to reuse the fast modular reduction in scalar multiplications. By optimizing the modular power computation in the decompression process, the steps are simplified and the modular multiplication can be reused. Under the TSMC 55 nm CMOS process, the area of the proposed hardware architecture is 7.46×105 equivalent gate, and the maximum frequency is up to 360 MHz. It can perform 9.06×104 key generations, 8.82×104 signatures and 3.99×104 verifications per second. -
表 1 Ed25519公钥生成算法流程
(1)选择256 bit私钥sk=(sk255, sk254,···, sk1, sk0)2； (2)对sk做SHA-512运算，即H(sk)= (h511,h510,···,h1,h0)2； (3)取H(sk)的低256 bit，并整理为s=(0,1,h253,h252,···,h3,0,0,0)2； (4)做标量乘A=sB=(x,y)，其中x=(x254,x253,···,x1,x0)2,
y=(y254,y253,···,y1,y0)2；(5)压缩sB结果，得公钥pk=(x0,y254,y253,···,y1,y0)2。 
下载: 导出CSV
表 2 Ed25519签名算法流程
(1)取H(sk)的高256 bit h=(h511,h510,···,h257,h256)2； (2)做SHA-512运算，r=H(h||M) mod L； (3)做标量乘R'=rB=(x,y)，其中x=(x254,x253,···,x1,x0)2, y=(y254,
y253,···,y1,y0)2；(4)压缩rB结果，得R=(x0,y254,y253,···,y1,y0)2； (5)做SHA-512运算，k=H(R||pk||M) mod L； (6)计算S= (r+ks) mod L； (7)返回签名结果(R||S)。
下载: 导出CSV
表 3 Ed25519验签算法流程
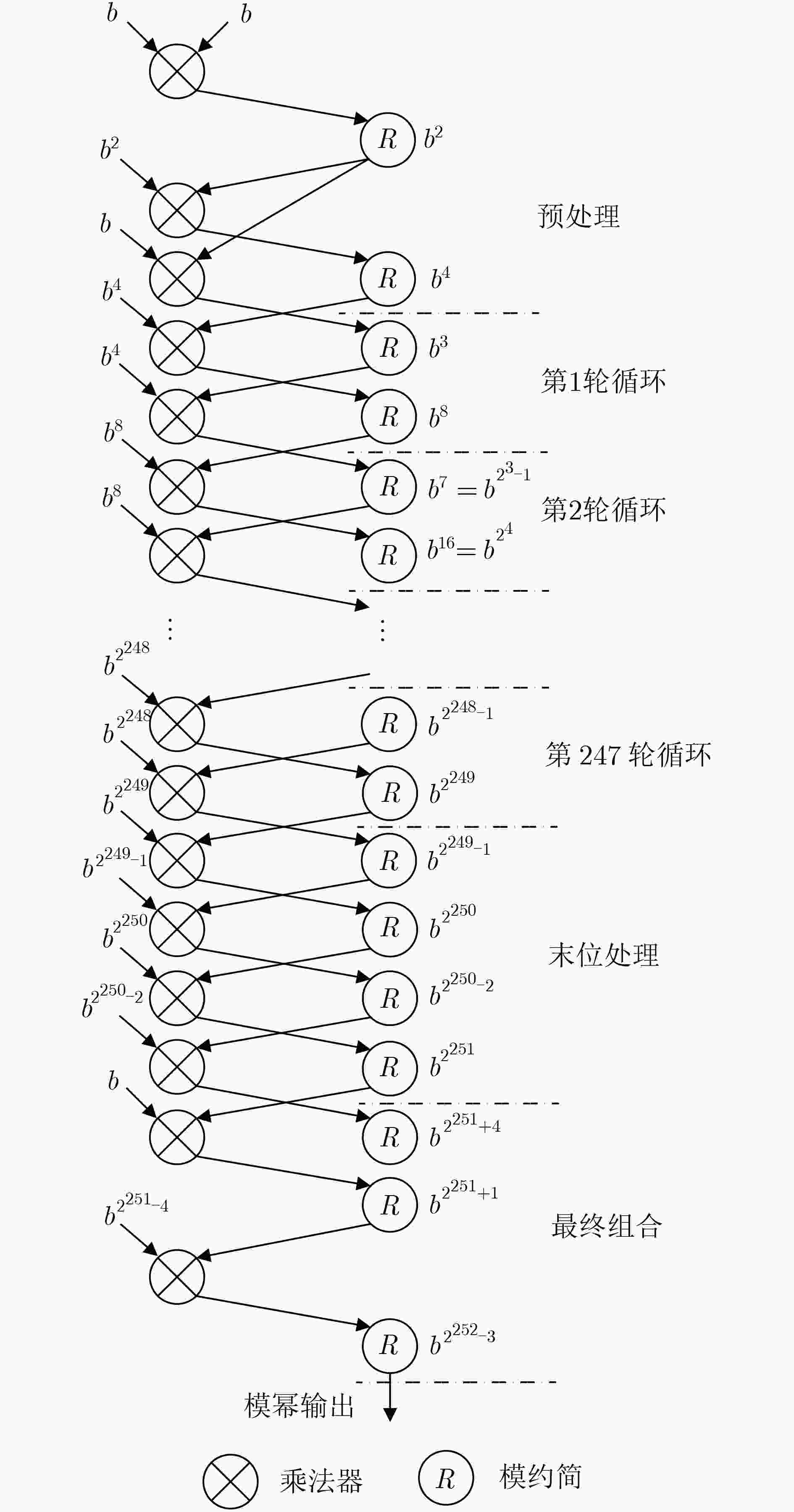
(1)解压R为点坐标R'； (2)解压pk为点坐标A； (3)做SHA-512运算，k=H(R||pk||M) mod L； (4)验证SB=R'+kA是否成立，若成立则验签成功。
下载: 导出CSV
表 4 宽度为2的窗口法
输入：255 bit二进制数k={k254k253···k1k0}，点加标志位n,
n∈{0,1}，椭圆曲线上任意点P1, P2。输出：标量乘Q=kP1+nP2 (1)预计算2P1,3P1，共2个点坐标； (2)若k254=0，则令Q=0，为无穷远点，若k254=1，则令Q=P1； (3)对于i从126～0，循环计算： Q=4Q； Q=Q+{k2i+1,k2i}P1； (4)若n=1，则计算：Q=Q+P2 //为适应验签算法； (5)返回Q值。
下载: 导出CSV
表 5 点加和倍点操作流程[14]
输入：P(X1,Y1,Z1,T1), Q(X2,Y2,Z2,T2) 输出：Q(X3,Y3,Z3,T3)=P+Q, Q(X3,Y3,Z3,T3)=2P (1) A=(Y1–X1)·(Y2–X2) A=(X1)2 (2) B=(Y1+X1)·(Y2+X2) B=(Y1)2 (3) C=T1·2·d·T2 C=2·(Z1)2 (4) D=Z1·2·Z2 H=A+B (5) E=B–A E=H–(X1+Y1)2 (6) F=D–C G=A–B (7) G=D+C F=C+G (8) H=B+A X3=E·F (9) X3=E·F Y3=G·H (10) Y3=G·H T3=E·H (11) T3=E·H Z3=F·G (12) Z3=F·G
下载: 导出CSV
表 6 倍点操作流程
输入：点坐标P(X1,Y1,Z1,T1), Q(X2,Y2,Z2,T2) 输出：Q(X3,Y3,Z3,T3)=2P 步骤 模乘 模加减 (1) A=X1·X1 (2) t1=Z1·Z1 (3) B=Y1·Y1 t2=X1+Y1 (4) t2=t2·t2 C=t1+t1, H=A+B, G=A–B (5) Y2=G·H E=H–t2, F=C+G (6) X2=E·F (7) Z2=F·G (8) T2=E·H (9) 等待T2约简
下载: 导出CSV
表 7 点加操作流程
输入：点坐标P(X1,Y1,Z1, T1)，Q(X2,Y2,Z2,T2) 输出：Q(X3,Y3,Z3,T3)=P+Q 步骤 模乘 模加减 (1) A1←Y1–X1, B1←Y1+X1 (2) A2←Y2–X2, B2←Y2+X2 (3) A←A1·A2 (4) B←B1·B2 t1=T1+T1 (5) t1←t1·d t2=Z1+Z1 (6) D←t2·Z2 (7) C←t1·T2 E←B–A, H←B+A (8) X3←E·H F←D–C, G←D+C (9) Y3←G·H (10) Z3←F·G (11) T3←E·H (12) 等待Z3约简
下载: 导出CSV
表 8 Ed25519快速约简算法
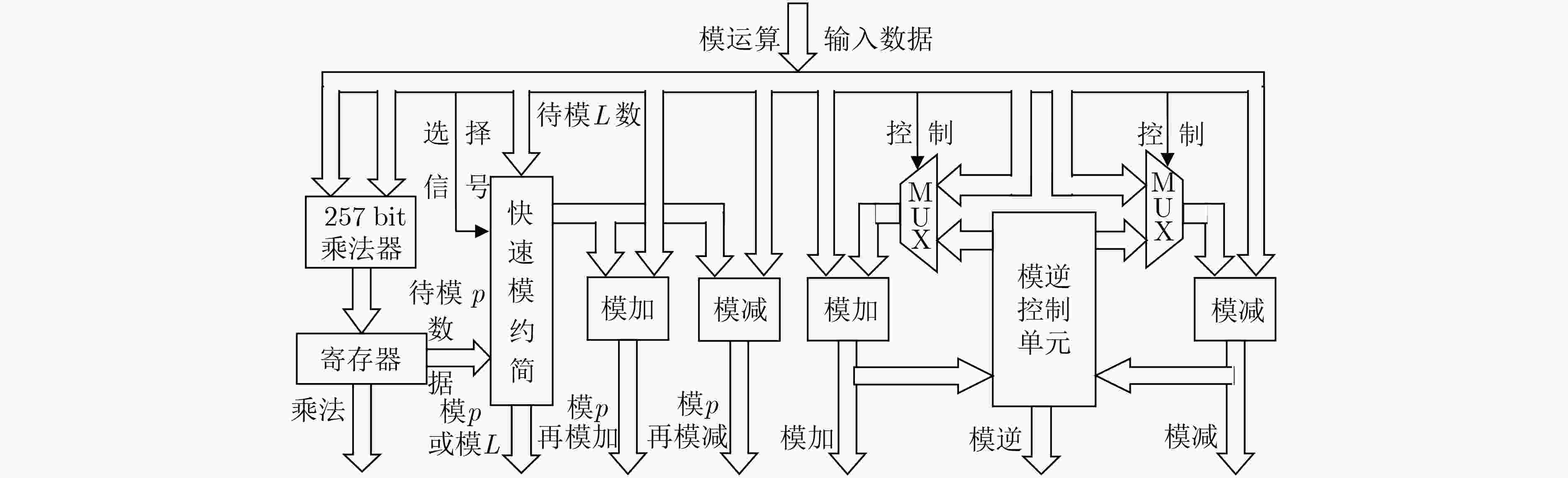
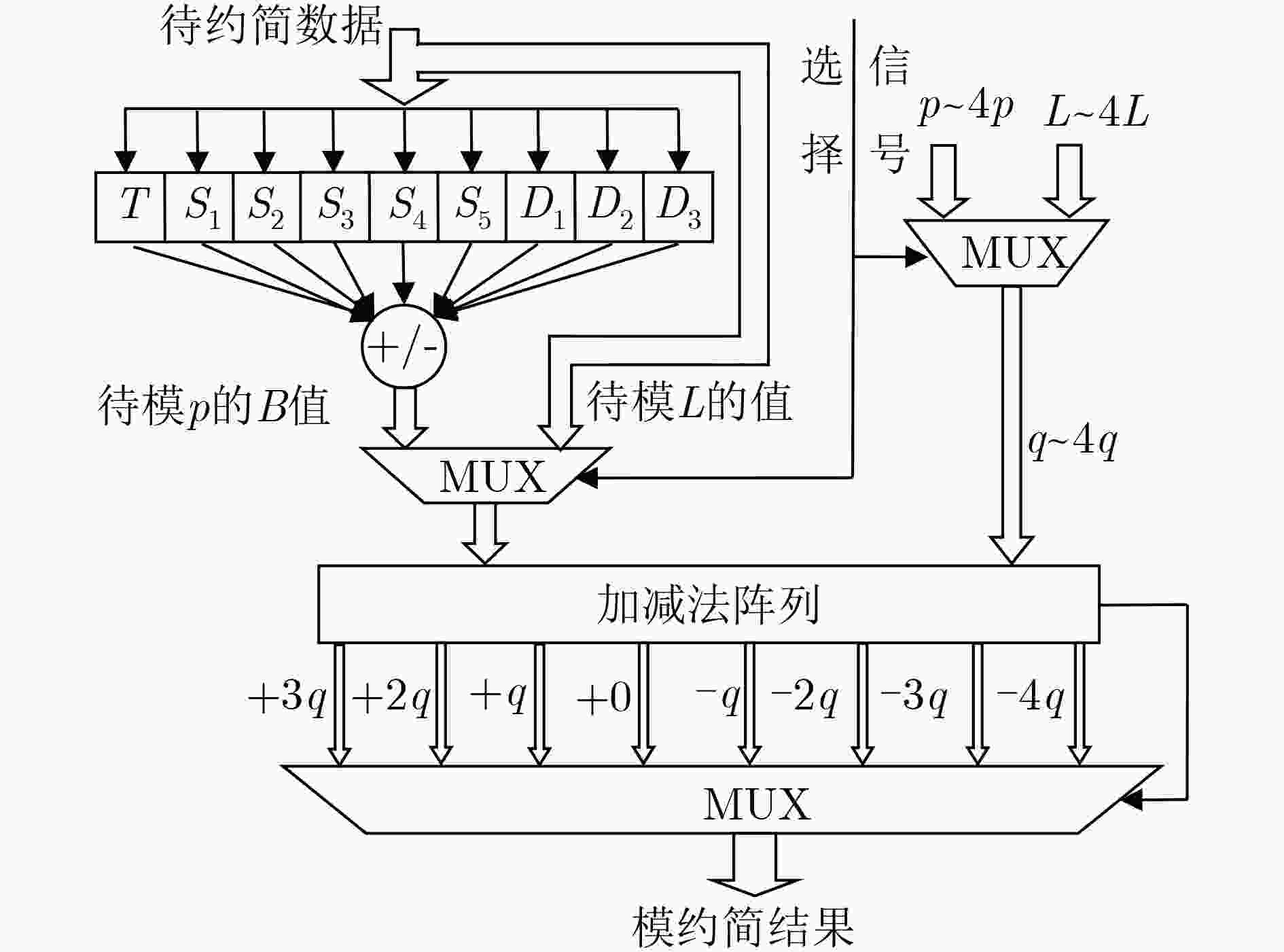
输入：A=(A254||A253||A252||···||A2||A1||A0) 输出：Q=A mod p (1) T=(A127|| A126|| A125|| ···|| A2|| A1|| A0) (2) S1=(A252|| A251|| A250|| ···|| A129|| A128||5′h0) (3) S2=(A253|| A252|| A251|| ···|| A129|| A128||3′h0) (4) S3=(247′h0|| A254|| A254||4′h0) (5) S4=(249′h0|| A253|| A253||2′h0) (6) S5=(249′h0|| A254|| 4′h0) (7) D1=(A254|| A253|| A252|| ···|| A129|| A128||1′h0) (8) D2=(253′h0|| A254) (9) D3=(253′h0|| A253) (10) Q=(T+S1+S2+S3+S4+S5–D1–D2–D3)mod p
下载: 导出CSV
表 9 基于Barrett约简的模L算法
输入：素数L, 512 bit数值a, T=[2512/(8L)] 输出：r=a mod L (1)q1=[a/2255]·T； (2)q2=[ q1/2257]·(8L)； (3)r=(a mod 2257)–(q2 mod 2257)； (4)若果r<0，则r=r+2257； (5)如果r≥8L，则r=r–11L，否则r=r–3L；//可复用快速模约简 (6)计算r=r mod L并返回r值。
下载: 导出CSV
表 11 周期及运算次数
平均周期 理论最大
周期平均每秒
运算次数理论最慢每秒
运算次数公钥生成 3237 3975 111.2×103 90.6×103 签名 3345 4083 107.6×103 88.2×103 验签 7488 9020 48.1×103 39.9×103
下载: 导出CSV
表 13 标量乘单元性能对比
器件 硬件开销Slices/LUT/FF/DSP/BRAM 周期数Cycles 折算值Slices×Cycles×10–6 本文 Zynq-7035 14759/52512/9342/225/0 3895 57.5 文献[8] Zynq-7020 775/2707/962/15/0 120260 93.2 文献[9]1) Zynq-7000 2170/8680/3472/0/0 86348 187.4 文献[9]2) Zynq-7000 2193/8770/3729/0/0 74783 189.3 文献[11] Zynq-7020 6161/17939/21077/175/0 10465 64.5 文献[12] Zynq-7020 1006/0/0/20/2 114980 115.7 文献[13] Zynq-7020 1029/2783/3592/20/2 79400 81.7 1)：采用D&A算法；2)：采用NAF算法
下载: 导出CSV
-
[1] RESCORLA E. IETF RFC 8446 The Transport Layer Security (TLS) protocol version 1.3[S]. 2018. [2] LANGLEY A, HAMBURG M, and TURNER S. IRTF RFC 7748 Elliptic curves for security[S]. 2016. [3] FAZ-HERNÁNDEZ A, LÓPEZ J, and DAHAB R. High-performance implementation of elliptic curve cryptography using vector instructions[J]. ACM Transactions on Mathematical Software, 2019, 45(3): 25.1–25.35. doi: 10.1145/3309759 [4] ISLAM M M, HOSSAIN M S, HASAN M K, et al. FPGA implementation of high-speed area-efficient processor for elliptic curve point multiplication over prime field[J]. IEEE Access, 2019, 7: 178811–178826. doi: 10.1109/ACCESS.2019.2958491 [5] 戴紫彬, 易肃汶, 李伟, 等. 椭圆曲线密码处理器的高效并行处理架构研究与设计[J]. 电子与信息学报, 2017, 39(10): 2487–2494. doi: 10.11999/JEIT161380DAI Zibin, YI Suwen, LI Wei, et al. Research and design of efficient parallel processing architecture for elliptic curve cryptographic processor[J]. Journal of Electronics &Information Technology, 2017, 39(10): 2487–2494. doi: 10.11999/JEIT161380 [6] KIM J, PARK J H, KIM D C, et al. Complete addition law for Montgomery curves[C]. The 22nd International Conference on Information Security and Cryptology– ICISC 2019, Seoul, South Korea, 2019: 260–277. doi: 10.1007/978-3-030-40921-0_16. [7] SALARIFARD R and BAYAT-SARMADI S. An efficient low-latency point-multiplication over curve25519[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2019, 66(10): 3854–3862. doi: 10.1109/TCSI.2019.2914247 [8] TURAN F and VERBAUWHEDE I. Compact and flexible FPGA implementation of Ed25519 and X25519[J]. ACM Transactions on Embedded Computing Systems, 2019, 18(3): 24. doi: 10.1145/3312742 [9] MEHRABI M A and DOCHE C. Low-cost, low-power FPGA implementation of ED25519 and CURVE25519 point multiplication[J]. Information, 2019, 10(9): 285. doi: 10.3390/info10090285 [10] 魏伟, 陈佳哲, 李丹, 等. 椭圆曲线Diffie-Hellman密钥交换协议的比特安全性研究[J]. 电子与信息学报, 2020, 42(8): 1820–1827. doi: 10.11999/JEIT190845WEI Wei, CHEN Jiazhe, LI Dan, et al. Research on the bit security of elliptic curve Diffie-Hellman[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1820–1827. doi: 10.11999/JEIT190845 [11] KOPPERMANN P, DE SANTIS F, HEYSZL J, et al. Low-latency X25519 hardware implementation: Breaking the 100 microseconds barrier[J]. Microprocessors and Microsystems, 2017, 52: 491–497. doi: 10.1016/j.micpro.2017.07.001 [12] SASDRICH P and GÜNEYSU T. Exploring RFC 7748 for hardware implementation: Curve25519 and Curve448 with side-channel protection[J]. Journal of Hardware and Systems Security, 2018, 2(4): 297–313. doi: 10.1007/s41635-018-0048-z [13] SASDRICH P and GÜNEYSU T. Implementing Curve25519 for side-channel--protected elliptic curve cryptography[J]. ACM Transactions on Reconfigurable Technology and Systems, 2015, 9(1): 3. doi: 10.1145/2700834 [14] JOSEFSSON S and LIUSVAARA I. IRTF RFC 8032 Edwards-curve digital signature algorithm (EdDSA)[S]. 2017. [15] VENGALA D V K, KAVITHA D, and KUMAR A P S. Secure data transmission on a distributed cloud server with the help of HMCA and data encryption using optimized CP-ABE-ECC[J]. Cluster Computing, 2020, 23(3): 1683–1696. doi: 10.1007/s10586-020-03114-1 [16] LI Hui. Pseudo-random scalar multiplication based on group isomorphism[J]. Journal of Information Security and Applications, 2020, 53: 102534. doi: 10.1016/j.jisa.2020.102534 [17] ZHANG Neng, YANG Bohan, CHEN Chen, et al. Highly efficient architecture of NewHope-NIST on FPGA using low-complexity NTT/INTT[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020, 2020(2): 49–72. doi: 10.13154/tches.v2020.i2.49-72 [18] HOSSAIN M S, KONG Yinan, SAEEDI E, et al. High-performance elliptic curve cryptography processor over NIST prime fields[J]. IET Computers & Digital Techniques, 2017, 11(1): 33–42. doi: 10.1049/iet-cdt.2016.0033 [19] KNEZEVIC M, VERCAUTEREN F, and VERBAUWHEDE I. Faster interleaved modular multiplication based on Barrett and Montgomery reduction methods[J]. IEEE Transactions on Computers, 2010, 59(12): 1715–1721. doi: 10.1109/TC.2010.93 -
下载:
图(4) / 表(13)
计量
- 文章访问数: 1623
- HTML全文浏览量: 801
- PDF下载量: 123
- 被引次数: 0
