Study on Coexistence of Multipe Attractors in Memristor-based Switching Chaotic Circuits
-
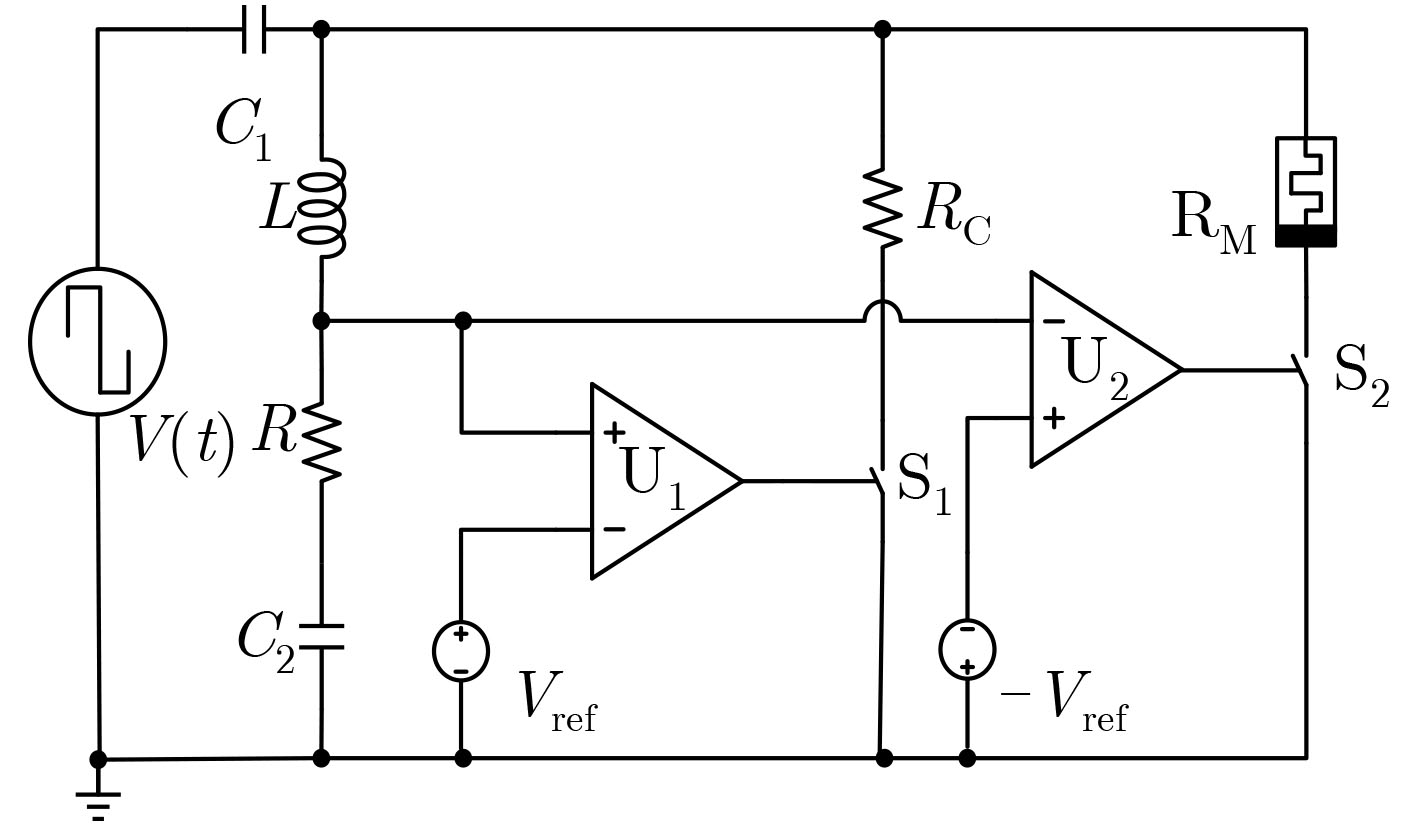
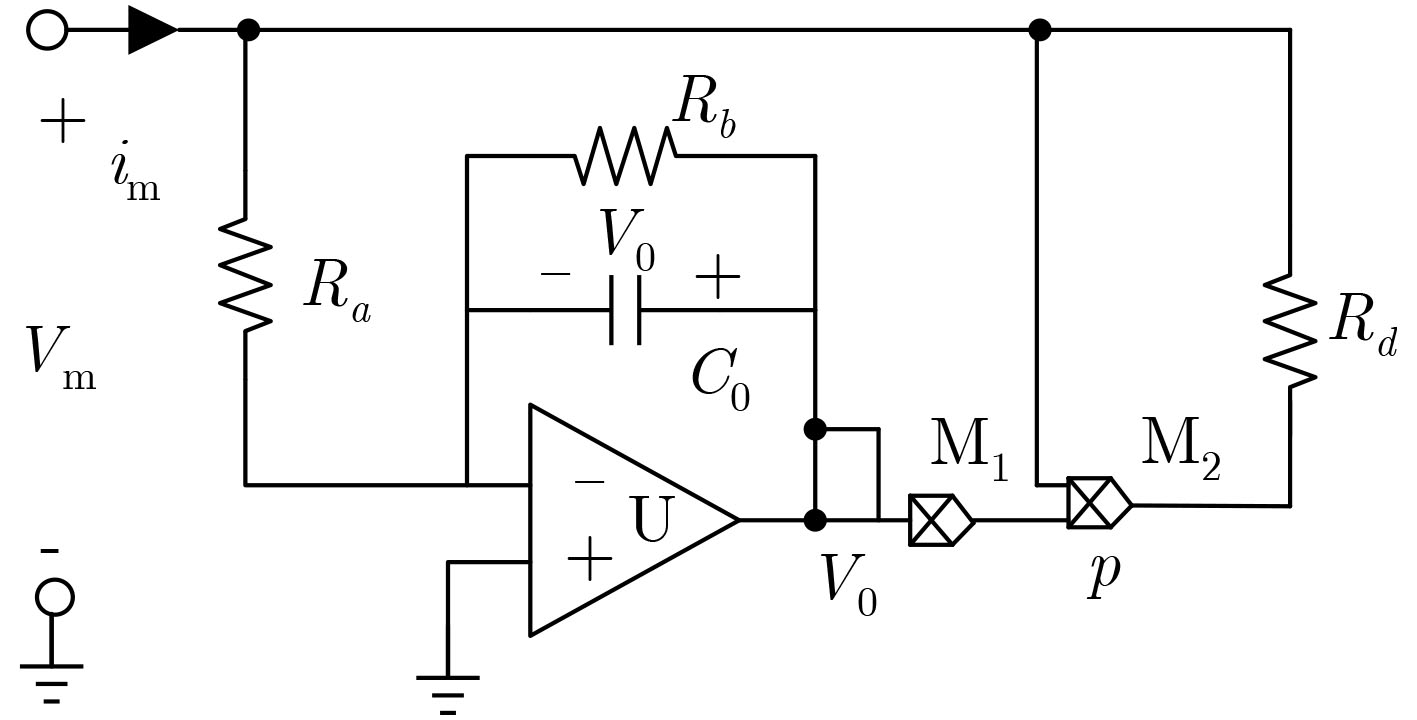
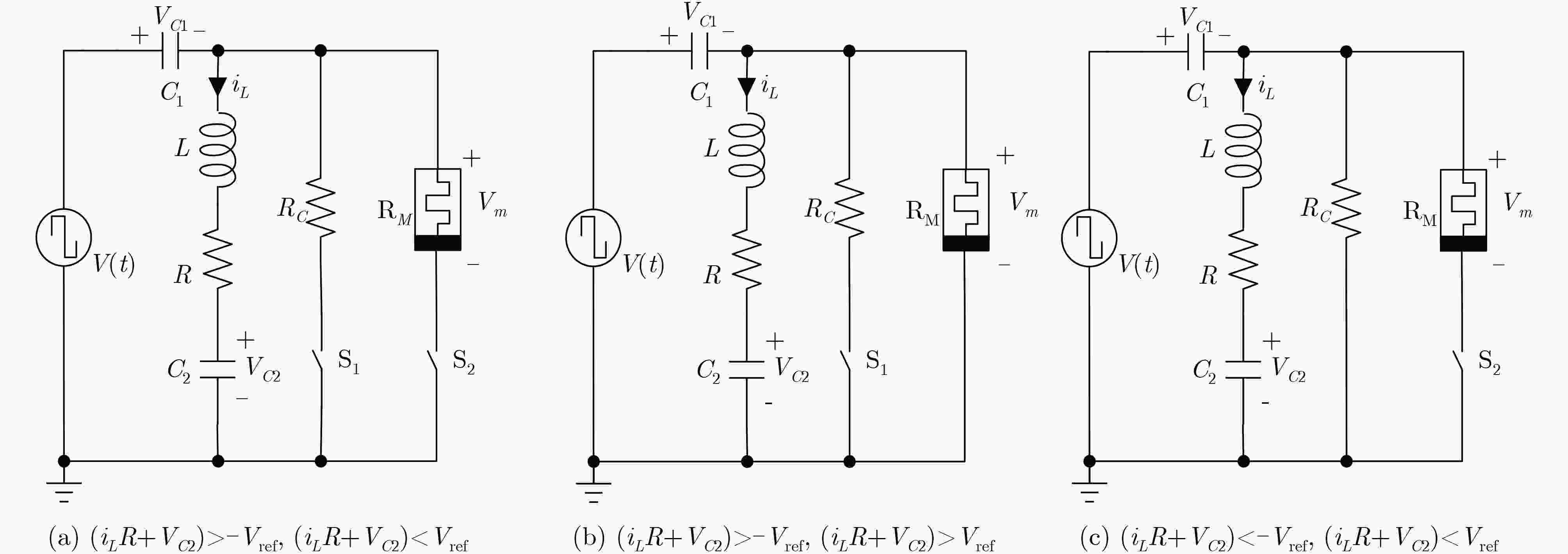
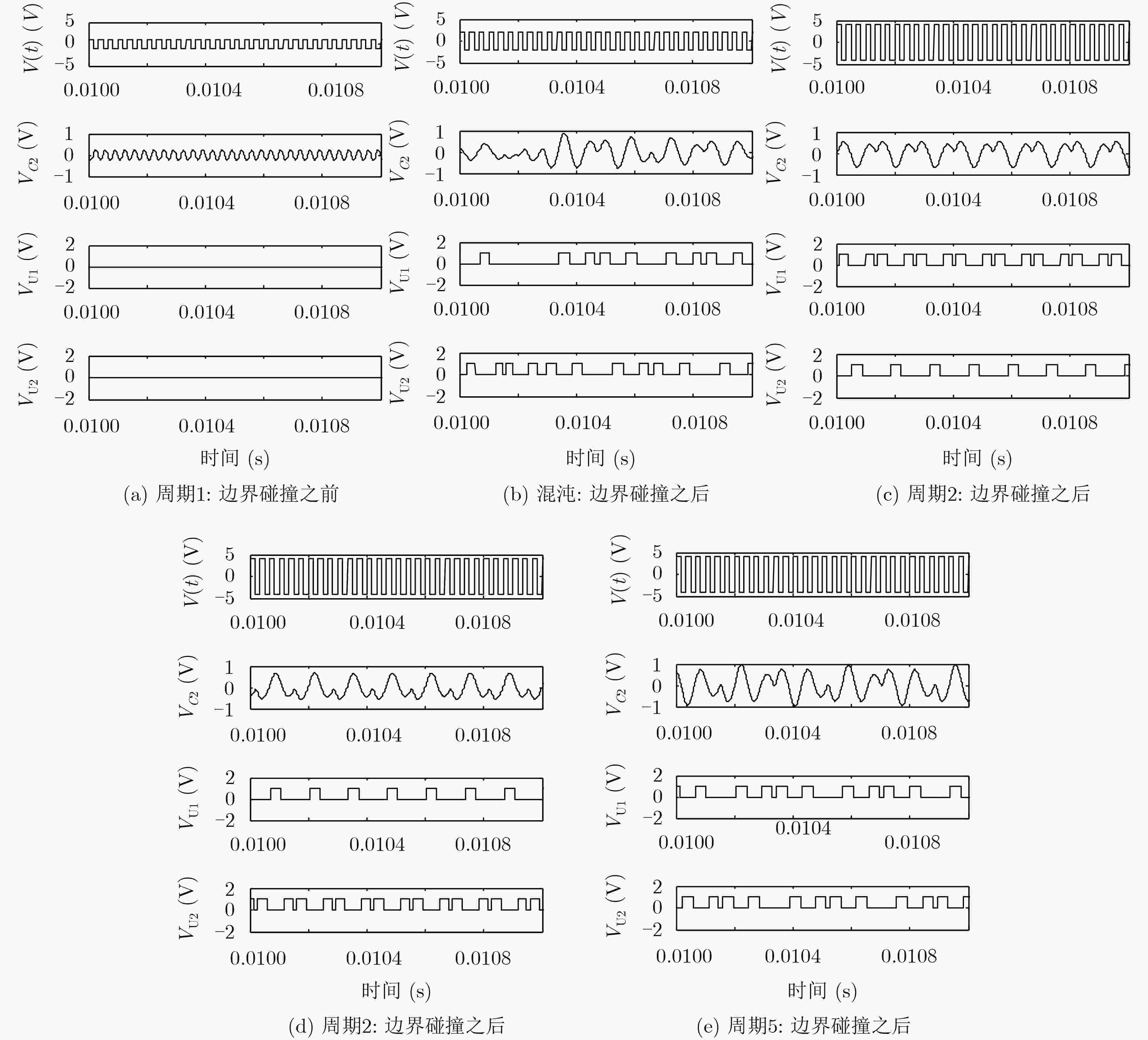
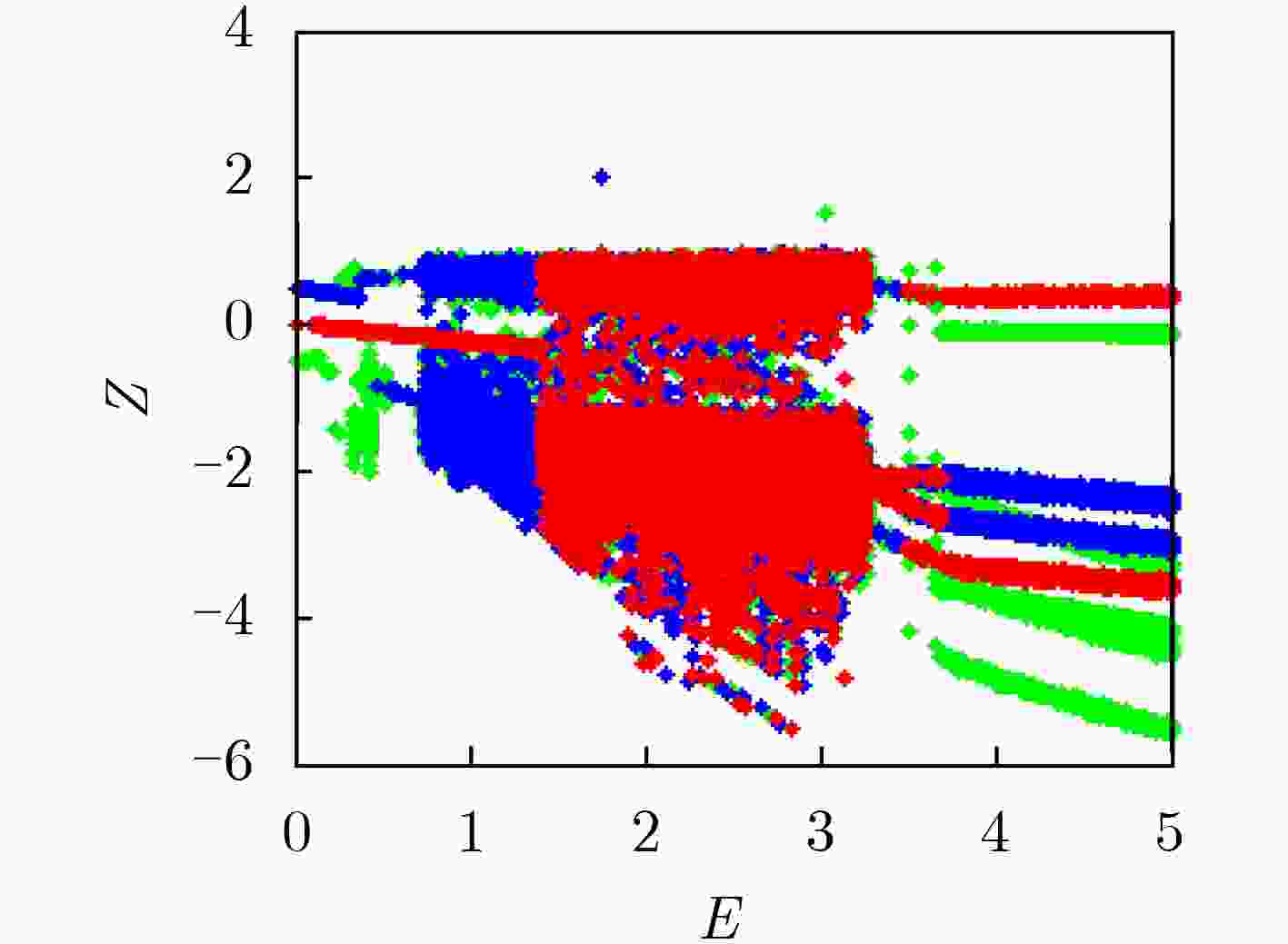
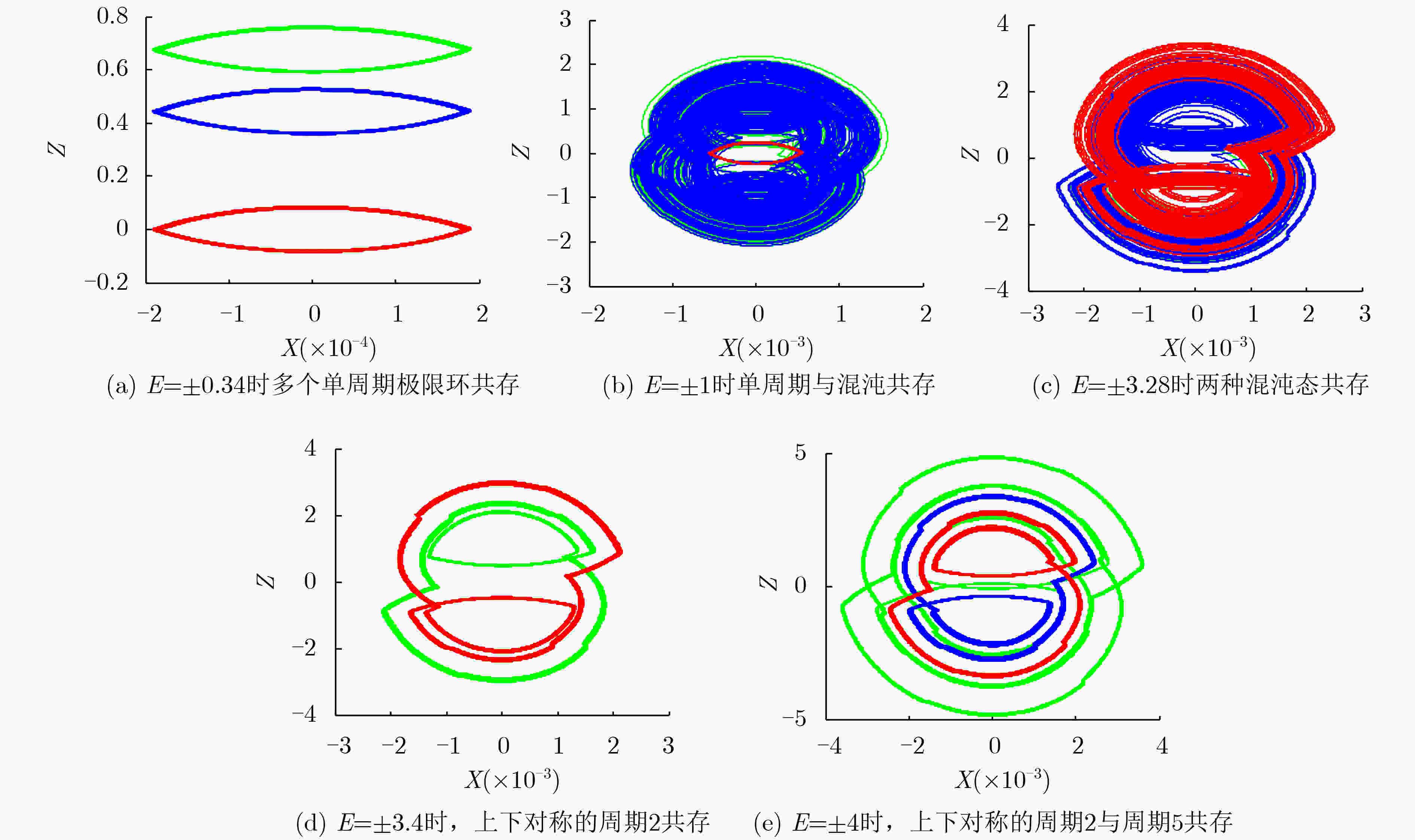
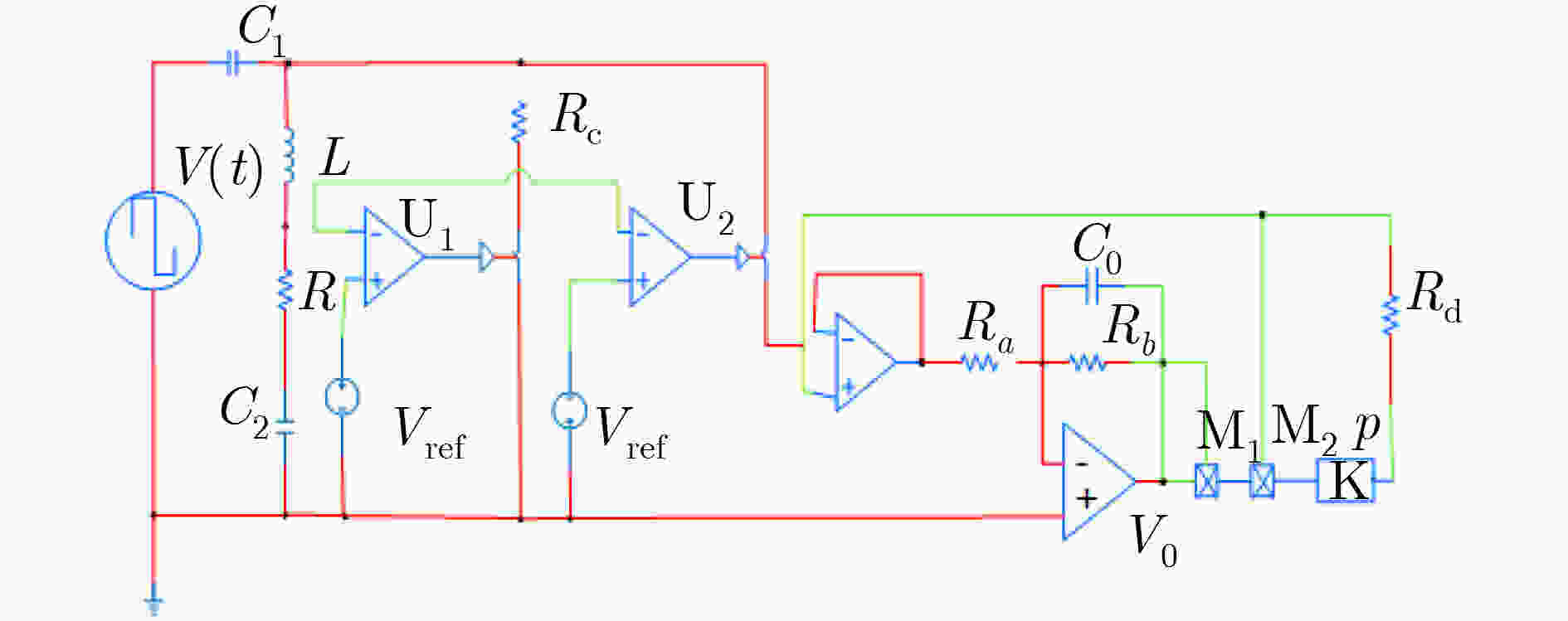
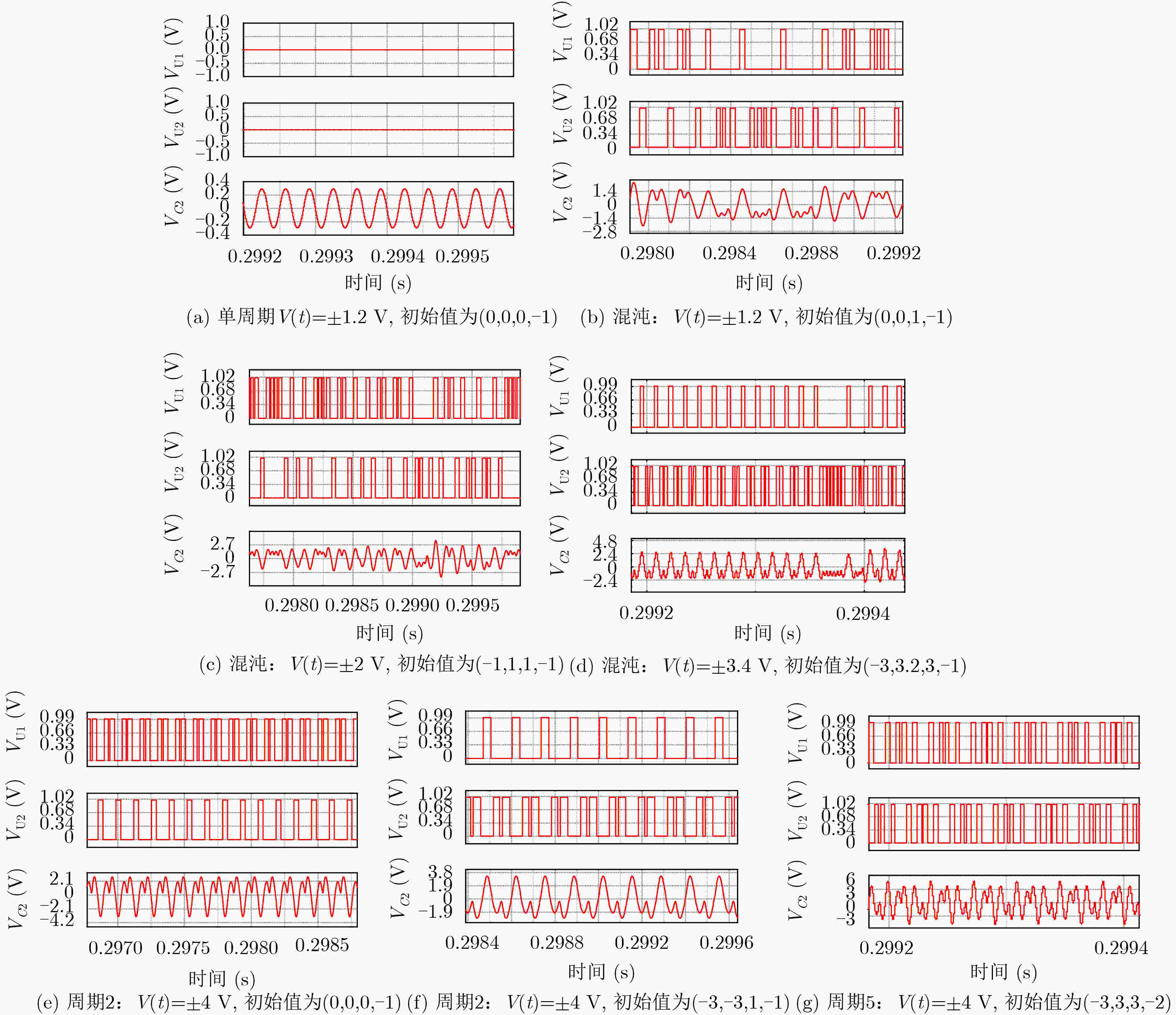
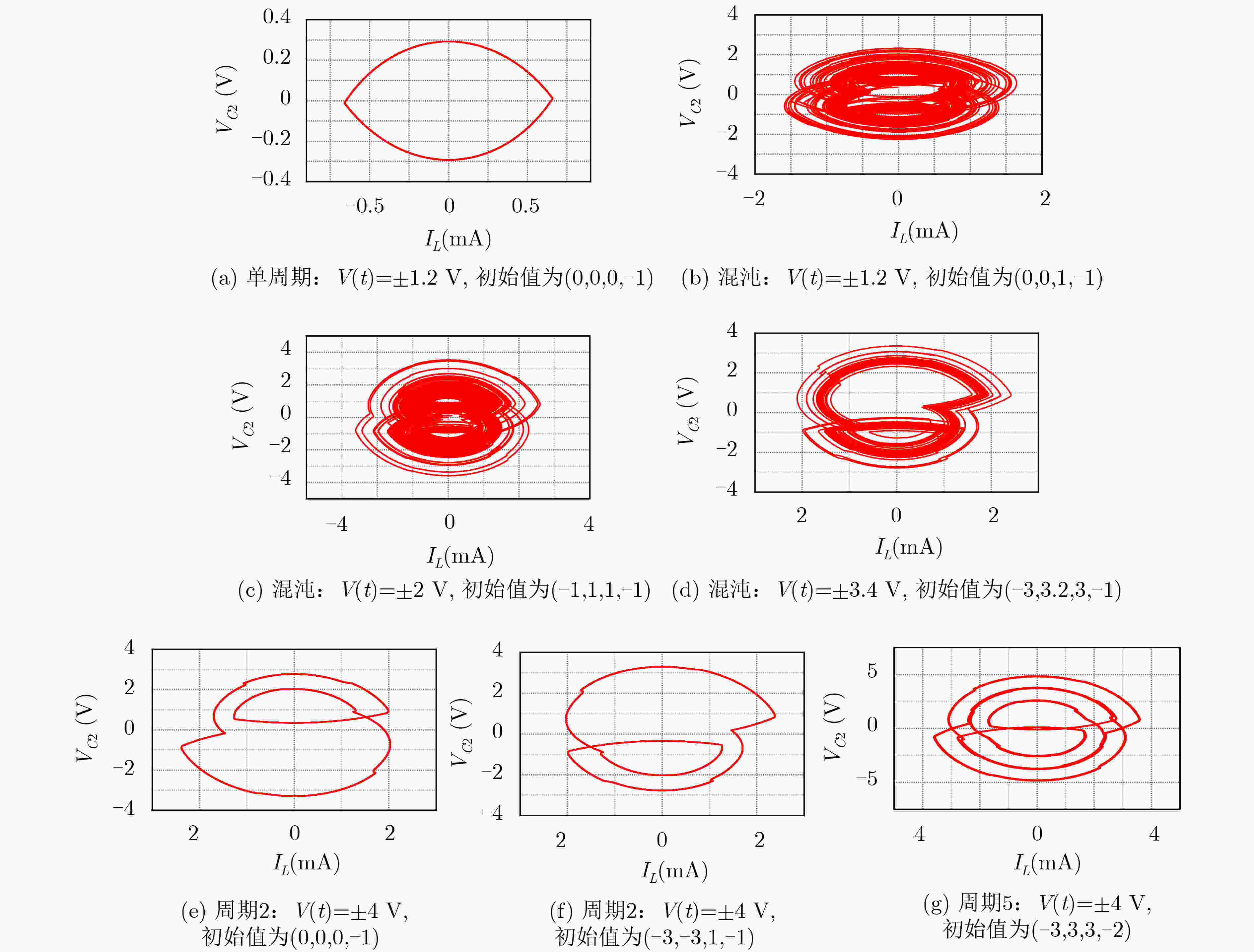
摘要: 为了研究忆阻开关电路的动力学行为,该文提出一种具有多吸引子共存现象的忆阻开关混沌电路。在该电路中存在多吸引子分岔,当系统中发生边界碰撞之后,系统中将产生不同的吸引子共存现象。其中包括单周期极限环与混沌吸引子共存,不同的混沌吸引子共存,对称的2周期极限环共存现象,以及对称的2周期极限环与5周期极限环共存现象等。该文通过相图、分岔图等数值仿真,分析了该电路的动力学行为,并利用PSIM电路仿真验证了其电路的可行性,对开关电路中多吸引子共存现象和混沌应用的研究具有重要意义。Abstract: In order to study the dynamic behavior of memristor switch circuit, a memristor-based switched chaotic circuit with multiple coexisting attractors is designed. There exists multiple attractor bifurcation in this circuit system. When boundary collisions occurs in the system, there are different attractors coexisting in the system. It includes the coexistence of the single periodic limit cycles with chaotic attractors, different chaotic attractors, symmetric 2-periodic limit cycles, and symmetric 2-periodic limit cycles with 5-periodic limit cycles. The dynamic behavior of the circuit system is analyzed by numerical simulation of phase diagram and bifurcation diagram. And the feasibility of the circuit is verified by PSIM circuit simulation, this paper is of great significance to the study of multiple attractor bifurcation in switching circuits and the application of chaos.
-
Key words:
- Memristor /
- Switching circuit /
- Multiple attractor bifurcation /
- Coexisting attractor
-
表 1 忆阻开关混沌电路的参数选取
参数 名称 取值 C1, C2 电容 10 nF L 电感 20 mH R 电阻 100 $\Omega $ RC 电阻 30 $\Omega $ Vref 参考电压 1 V Ra, Rb 电阻 1 k $\Omega $ Rd 电阻 30 $\Omega $ C0 电容 20 nF p 比例因子 –0.5 -
[1] CHUA L. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–519. doi: 10.1109/TCT.1971.1083337 [2] STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. doi: 10.1038/nature06932 [3] YANG Feifei, MOU Jun, SUN Kehui, et al. Color image compression-encryption algorithm based on fractional-order memristor chaotic circuit[J]. IEEE Access, 2019, 7: 58751–58763. doi: 10.1109/ACCESS.2019.2914722 [4] 牛莹, 张勋才. 基于变步长约瑟夫遍历和DNA动态编码的图像加密算法[J]. 电子与信息学报, 2020, 42(6): 1383–1391. doi: 10.11999/JEIT190849NIU Ying and ZHANG Xuncai. Image encryption algorithm of based on variable step length Josephus traversing and DNA dynamic coding[J]. Journal of Electronics &Information Technology, 2020, 42(6): 1383–1391. doi: 10.11999/JEIT190849 [5] DUAN Shukai, HU Xiaofang, DONG Zhekang, et al. Memristor-based cellular nonlinear/neural network: Design, analysis, and applications[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(6): 1202–1213. doi: 10.1109/TNNLS.2014.2334701 [6] YAO Wei, WANG Chunhua, CAO Jinde, et al. Hybrid multisynchronization of coupled multistable memristive neural networks with time delays[J]. Neurocomputing, 2019, 363: 281–294. doi: 10.1016/j.neucom.2019.07.014 [7] ZHANG Xiaohong and LONG Keliu. Improved learning experience memristor model and application as neural network synapse[J]. IEEE Access, 2019, 7: 15262–15271. doi: 10.1109/ACCESS.2019.2894634 [8] TAN Yumei and WANG Chunhua. A simple locally active memristor and its application in HR neurons[J]. Chaos, 2020, 30(5): 053118. doi: 10.1063/1.5143071 [9] 贺利芳, 陈俊, 张天骐. 短参考多用户差分混沌移位键控通信系统性能分析[J]. 电子与信息学报, 2020, 42(8): 1902–1909. doi: 10.11999/JEIT190117HE Lifang, CHEN Jun, and ZHANG Tianqi. Performance analysis of short reference multi-user differential chaos shift keying communication system[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1902–1909. doi: 10.11999/JEIT190117 [10] TOLBA M F, SAYED W S, FOUDA M E, et al. Digital emulation of a versatile memristor with speech encryption application[J]. IEEE Access, 2019, 7: 174280–174297. doi: 10.1109/ACCESS.2019.2957300 [11] LIU Gongzhi, ZHENG Lijing, WANG Guangyi, et al. A carry lookahead adder based on hybrid CMOS-Memristor logic circuit[J]. IEEE Access, 2019, 7: 43691–43696. doi: 10.1109/ACCESS.2019.2907976 [12] MIN Xiaotao, WANG Xiaoyuan, ZHOU Pengfei, et al. An optimized memristor-based hyperchaotic system with controlled hidden attractors[J]. IEEE Access, 2019, 7: 124641–124646. doi: 10.1109/ACCESS.2019.2938183 [13] JIN Peipei, WANG Guangyi, IU H H C, et al. A locally active memristor and its application in a chaotic circuit[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2018, 65(2): 246–250. doi: 10.1109/TCSII.2017.2735448 [14] BAO B C, LIU Z, and XU J P. Steady periodic memristor oscillator with transient chaotic behaviours[J]. Electronics Letters, 2010, 46(3): 228–230. doi: 10.1049/el.2010.3114 [15] 谭志平, 曾以成, 李志军, 等. 浮地型忆阻器混沌电路的分析与实现[J]. 仪器仪表学报, 2014, 35(9): 2123–2129.TAN Zhiping, ZENG Yicheng, LI Zhijun, et al. Analysis and implementation of a floating memristor chaotic circuit[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 2123–2129. [16] WANG Chunhua, LIU Xiaoming, and XIA Hu. Multi-piecewise quadratic nonlinearity memristor and its 2N-scroll and 2N+1-scroll chaotic attractors system[J]. Chaos, 2017, 27(3): 033114. doi: 10.1063/1.4979039 [17] BAO Bocheng, WANG Ning, XU Quan, et al. A simple third-order memristive band pass filter chaotic circuit[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2017, 64(8): 977–981. doi: 10.1109/TCSII.2016.2641008 [18] LAI Qiang, KUATE P D K, LIU Feng, et al. An extremely simple chaotic system with infinitely many coexisting attractors[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2020, 67(6): 1129–1133. doi: 10.1109/TCSII.2019.2927371 [19] CHIN W, OTT E, NUSSE H E, et al. Grazing bifurcations in impact oscillators[J]. Physical Review E, 1994, 50(6): 4427–4444. doi: 10.1103/PhysRevE.50.4427 [20] SETH S and BANERJEE S. Study of an inductorless chaos generator[J]. Proc. Conf. Nonlin. Syst. Dyn. IISER Kolkata, 2016, 16(8): 1–18. [21] OHNISHI M and INABA N. A singular bifurcation into instant chaos in a piecewise-linear circuit[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications, 1994, 41(6): 433–442. doi: 10.1109/81.295239 [22] BANERJEE S and CHAKRABARTY K. Nonlinear modeling and bifurcations in the boost converter[J]. IEEE Transactions on Power Electronics, 1998, 13(2): 252–260. doi: 10.1109/63.662832 [23] BANERJEE S, PARUI S, and GUPTA A. Dynamical effects of missed switching in current-mode controlled DC–DC converters[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2004, 51(12): 649–654. doi: 10.1109/TCSII.2004.838438 [24] DUTTA M, NUSSE H E, OTT E, et al. Multiple attractor bifurcations: A source of unpredictability in piecewise smooth systems[J]. Physical Review Letters, 1999, 83(21): 4281–4284. doi: 10.1103/PhysRevLett.83.4281 [25] SETH S and BANERJEE S. Experimental observation of multiple attractor bifurcation in an electronic circuit[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2018, 65(9): 1254–1258. doi: 10.1109/TCSII.2018.2828409 -





 下载:
下载:


 下载:
下载:
