Study on OTFS Channel Estimation Algorithms in High-Speed Mobile Communication Systems
-
摘要: 针对高速移动环境中双色散信道会出现信道估计可靠性下降的问题,该文在正交时频空(OTFS)调制系统的输入-输出模型中提出一种基于压缩感知的信道估计算法。该算法利用信道中最大多普勒频移和最大时延确定导频发送矩阵的大小,相比传统的正交匹配追踪(OMP)信道估计算法,能够在保证相似信道估计准确度的情况下节省导频资源;并在此基础上,对OTFS调制符号做相位旋转,增加差分矩阵的秩,理论分析和仿真结果表明,该方案能够提升OTFS系统的分集阶数进而降低噪声的干扰。Abstract: In view of the problem that dual-dispersion channels will reduce the reliability of channel estimation in high-speed mobile environments, a channel estimation algorithm based on compressed sensing is proposed in the input-output model of Orthogonal Time-Frequency-Space (OTFS) modulation system. The maximum Doppler shift and the maximum delay in the channel are employed to determine the size of the pilot transmission matrix in the algorithm. Compared with the traditional Orthogonal Matching Pursuit (OMP) channel estimation algorithms, the pilot resources can be saved in the proposed algorithm while the accuracy of similar channel estimation is guaranteed. Furthermore, the phase rotation of the OTFS modulation symbols is used to improve the rank of the differential matrix. Theoretical analysis and simulation results show that the diversity order of the OTFS system is improved and noise interference is reduced.
-
表 1 本文PRS-OMP信道估计算法步骤
步骤 操作 描述 1 初始化 传感矩阵${\boldsymbol{X}}_{\bf{p}}^{\rm{T}}$,采样向量${\boldsymbol{y}}_{\bf{p}}^{\rm{T}}$,残差能量阈值为$\varepsilon $(足够小);残差${{\boldsymbol{r}}_0} = {\boldsymbol{y}}_{\bf{p}}^{\rm{T}}$,索引集${ { \boldsymbol{\varLambda } }_{\rm{0} } } = \varphi$(空集),$t = 1$ 2 时延多普勒路径匹配 找出残差${\boldsymbol{r}}$和传感矩阵${\boldsymbol{X}}_{\bf{p}}^{\rm{T}}$列向量内积中最大值所对应的脚标${\lambda _t} = \arg {\max _{j = \left( {1, \cdots ,N} \right)}}\left| {\left\langle {{{\boldsymbol{r}}_{t - {\rm{1}}}},{\boldsymbol{X}}_{\bf{p}}^{\rm{T}}\left[ j \right]} \right\rangle } \right|$ 3 记录路径,并建立路径对应的传感矩阵列向量集合 更新索引集${{\boldsymbol{\varLambda}} _t} = {{\boldsymbol{\varLambda}} _{t - 1}} \cup \{ {\lambda _t}\} $,记录找到的传感矩阵中的重建原子集合${\boldsymbol{X}}_{{\bf{p}},t}^{\rm{T}} = \left[ {{\boldsymbol{X}}_{{\bf{p}},t{\rm{ - 1}}}^{\rm{T}},{\boldsymbol{X}}_{_{\bf{p}}}^{\rm{T}}\left[ {{\lambda _t}} \right]} \right]$ 4 计算信道增益 由最小二乘[21]得到${\hat {\boldsymbol{h}}'_{{\bf{p}},t}} = \arg \min {\left\| {{\boldsymbol{y}}_{\bf{P}}^{\rm{T}} - {\boldsymbol{X}}_{{\bf{p}},t}^{\rm{T}}{{\hat {\boldsymbol{h}}'}_{{\bf{p}},t}}} \right\|_2}$ 5 更新残差 ${{\boldsymbol{r}}_t} = {\boldsymbol{y}}_{\bf{P}}^{\rm{T}} - {\boldsymbol{X}}_{{\bf{p}},t}^{\rm{T}}{\hat {\boldsymbol{h}}'_{{\bf{p}},t}}$, $t = t + 1$ 6 判断迭代条件 判断是否满足${\left\| {{{\boldsymbol{r}}_t}} \right\|_2} \le \varepsilon $,若满足,则停止迭代;若不满足,则执行步骤2 7 输出对应路径的信道增益 输出:${{\boldsymbol{h}}'_{\bf{p}}}$的$P$-稀疏的逼近元${\hat {\boldsymbol{h}}'_{{\bf{p}},t}}$ 表 2 仿真参数设置
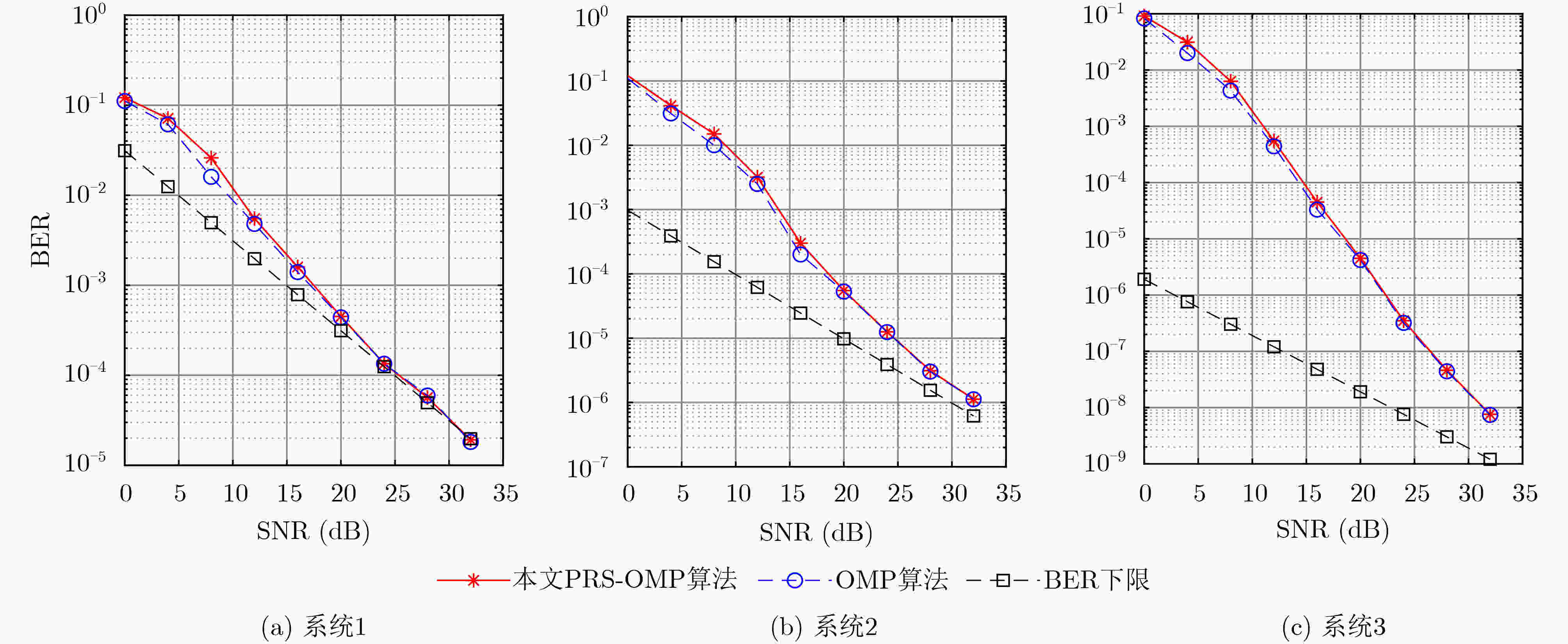
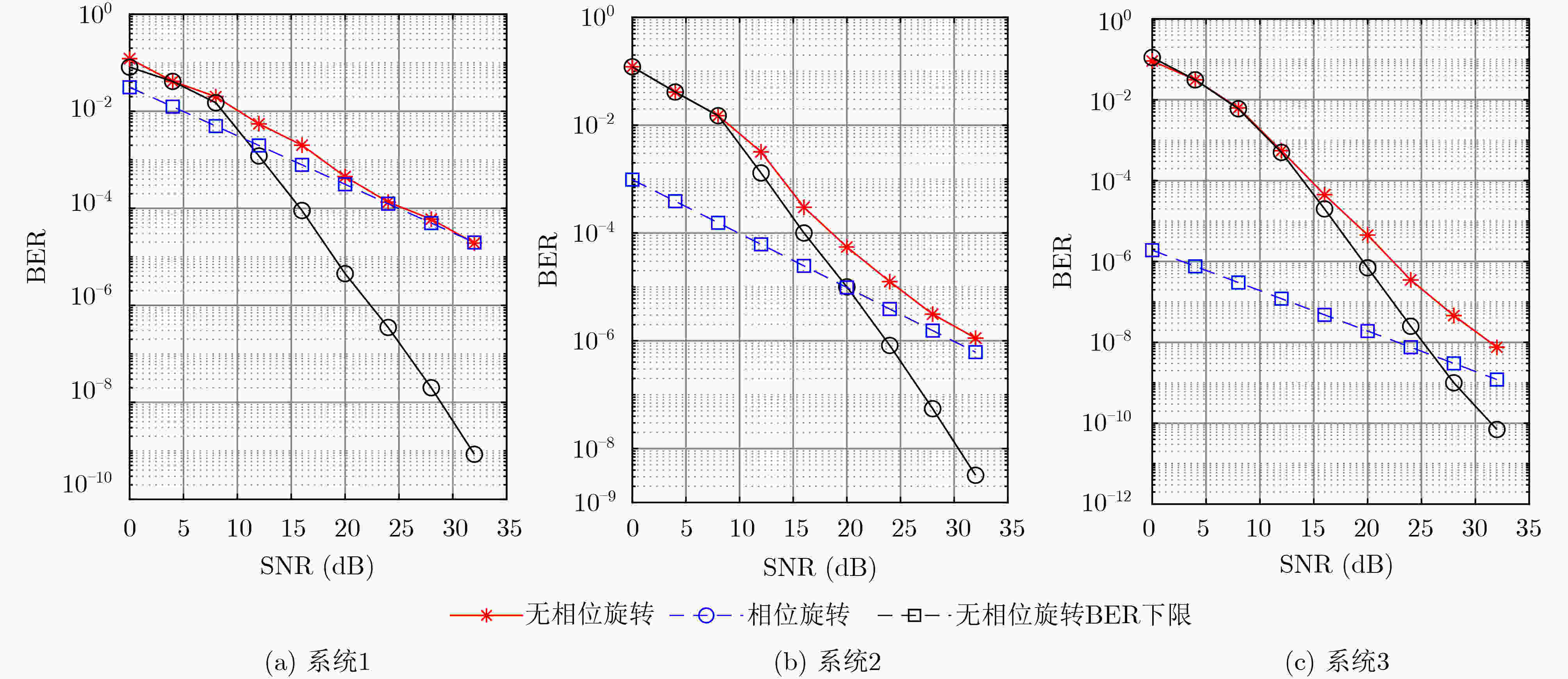
系统 载波频率(GHz) 子载波间隔(kHz) $M$ $N$ 路径数$P$ 调制方式 最大速度(km/h) PRS-OMP降导频资源率(%) 系统1 4 3.75 2 2 4 BPSK 506.250 100.00 系统2 4 3.75 4 2 4 BPSK 506.250 56.25 系统3 4 3.75 4 4 4 BPSK 253.125 14.06 -
[1] FARHANG A, REZAZADEHREYHANI A, DOYLE L E, et al. Low complexity modem structure for OFDM- based orthogonal time frequency space modulation[J]. IEEE Wireless Communications Letters, 2018, 7(3): 344–347. doi: 10.1109/LWC.2017.2776942 [2] 杨若男, 张伟涛, 楼顺天. 基于平行因子分析的SIMO-OFDM系统盲信道与符号联合估计算法[J]. 电子与信息学报, 2019, 41(3): 551–555. doi: 10.11999/JEIT180432YANG Ruonan, ZHANG Weitao, and LOU Shuntian. Joint blind channel estimation and symbols detection for SIMO-OFDM systems based on PARAFAC[J]. Journal of Electronics &Information Technology, 2019, 41(3): 551–555. doi: 10.11999/JEIT180432 [3] JEON W G, CHANG K H, and CHO Y S. An equalization technique for orthogonal frequency-division multiplexing systems in time-variant multipath channels[J]. IEEE Transactions on Communications, 1999, 47(1): 27–32. doi: 10.1109/26.747810 [4] CAI Xiaodong and GIANNAKIS G B. Bounding performance and suppressing intercarrier interference in wireless mobile OFDM[J]. IEEE Transactions on Communications, 2003, 51(12): 2047–2056. doi: 10.1109/TCOMM.2003.820752 [5] SCHNITER P. Low-complexity equalization of OFDM in doubly selective channels[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 1002–1011. doi: 10.1109/TSP.2004.823503 [6] DAS S and SCHNITER P. Max-SINR ISI/ICI-shaping multicarrier communication over the doubly dispersive channel[J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5782–5795. doi: 10.1109/TSP.2007.901660 [7] CHOI Y S, VOLTZ P J, and CASSARA F A. On channel estimation and detection for multicarrier signals in fast and selective Rayleigh fading channels[J]. IEEE Transactions on Communications, 2001, 49(8): 1375–1387. doi: 10.1109/26.939860 [8] MOLISCH A F, TOELTSCH M, and VERMANI S. Iterative methods for cancellation of intercarrier interference in OFDM systems[J]. IEEE Transactions on Vehicular Technology, 2007, 56(4): 2158–2167. doi: 10.1109/TVT.2007.897628 [9] FANG Kun, RUGINI L, and LEUS G. Low-complexity block turbo equalization for OFDM systems in time-varying channels[C]. 2007 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Honolulu, USA, 2008: 5555–5566. doi: 10.1109/ICASSP.2007.366568. [10] ZHAO Yuping and HAGGMAN S G. Intercarrier interference self-cancellation scheme for OFDM mobile communication systems[J]. IEEE Transactions on Communications, 2001, 49(7): 1185–1191. doi: 10.1109/26.935159 [11] SEATON K A and ARMSTRONG J. Polynomial cancellation coding and finite differences[J]. IEEE Transactions on Information Theory, 2000, 46(1): 311–313. doi: 10.1109/18.817533 [12] KOZEK W and MOLISCH A F. Nonorthogonal pulseshapes for multicarrier communications in doubly dispersive channels[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(8): 1579–1589. doi: 10.1109/49.730463 [13] LIU Ke, KADOUS T, and SAYEED A M. Orthogonal time-frequency signaling over doubly dispersive channels[J]. IEEE Transactions on Information Theory, 2004, 50(11): 2583–2603. doi: 10.1109/TIT.2004.836931 [14] WANG Zhaohui, ZHOU Shengli, GIANNAKIS G B, et al. Frequency-domain oversampling for zero-padded OFDM in underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2012, 37(1): 14–24. doi: 10.1109/JOE.2011.2174070 [15] XIA Xianggen. Precoded and vector OFDM robust to channel spectral nulls and with reduced cyclic prefix length in single transmit antenna systems[J]. IEEE Transactions on Communications, 2001, 49(8): 1363–1374. doi: 10.1109/26.939855 [16] EBIHARA T and LEUS G. Doppler-resilient orthogonal signal-division multiplexing for underwater acoustic communication[J]. IEEE Journal of Oceanic Engineering, 2016, 41(2): 408–427. doi: 10.1109/JOE.2015.2454411 [17] EBIHARA T and MIZUTANI K. Underwater acoustic communication with an orthogonal signal division multiplexing scheme in doubly spread channels[J]. IEEE Journal of Oceanic Engineering, 2014, 39(1): 47–58. doi: 10.1109/JOE.2013.2245273 [18] 崔维嘉, 张鹏, 巴斌. 基于贝叶斯自动相关性确定的稀疏重构正交频分复用信号时延估计算法[J]. 电子与信息学报, 2019, 41(10): 2318–2324. doi: 10.11999/JEIT181181CUI Weijia, ZHANG Peng, and BA Bin. Sparse reconstruction OFDM delay estimation algorithm based on bayesian automatic relevance determination[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2318–2324. doi: 10.11999/JEIT181181 [19] 叶新荣, 朱卫平, 张爱清, 等. OFDM系统双选择性慢衰落信道的压缩感知估计[J]. 电子与信息学报, 2015, 37(1): 169–174. doi: 10.11999/JEIT140247YE Xinrong, ZHU Weiping, ZHANG Aiqing, et al. Compressed sensing based on doubly-selective slow-fading channel estimation in OFDM systems[J]. Journal of Electronics &Information Technology, 2015, 37(1): 169–174. doi: 10.11999/JEIT140247 [20] SHEN Wenqian, DAI Linglong, AN Jianping, et al. Channel estimation for Orthogonal Time Frequency Space (OTFS) massive MIMO[J]. IEEE Transactions on Signal Processing, 2019, 67(16): 4204–4217. doi: 10.1109/TSP.2019.2919411 [21] 黄敏, 李兵兵. 基于整体最小二乘的联合信道估计及OFDM信号检测算法[J]. 电子与信息学报, 2014, 36(6): 1448–1453. doi: 10.3724/SP.J.1146.2013.01327HUANG Min and LI Bingbing. Joint channel estimation and OFDM signals detection based on total least square[J]. Journal of Electronics &Information Technology, 2014, 36(6): 1448–1453. doi: 10.3724/SP.J.1146.2013.01327 [22] SURABHI G D, AUGUSTINE R M, and CHOCKALINGAM A. On the diversity of uncoded OTFS modulation in doubly-dispersive channels[J]. IEEE Transactions on Wireless Communications, 2019, 18(6): 3049–3063. doi: 10.1109/TWC.2019.2909205 [23] DAMEN M O, TEWFIK A, and BELFLORE J C. A construction of a space-time code based on number theory[J]. IEEE Transactions on Information Theory, 2002, 48(3): 753–760. doi: 10.1109/18.986032 -






 下载:
下载:


 下载:
下载:
