DDoS Attack Detection Model Parameter Update Method Based on EWC Algorithm
-
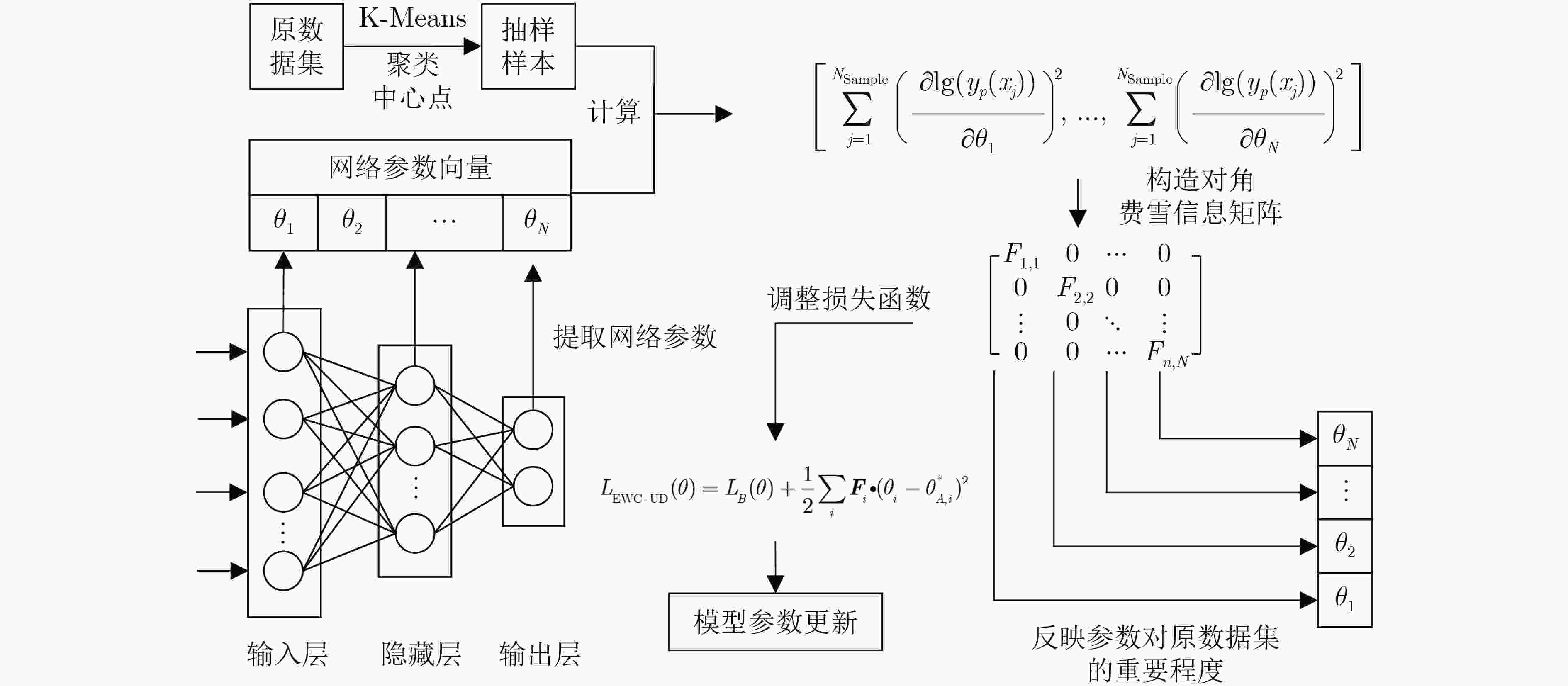
摘要: 针对现有基于多层线性感知器(Multi-Layer Perceptron, MLP)神经网络的DDoS攻击检测模型参数更新方法(MLP-UD)易遗忘模型训练原参数所用的DDoS攻击数据集(原数据集)知识、时间空间开销大的问题,该文提出一种基于弹性权重保持(Elastic Weight Consolidation, EWC)算法的模型参数更新方法(EWC-UD)。首先,使用K-Means算法计算原数据集聚类簇中心点作为费雪信息矩阵计算样本,有效提升计算样本均匀度与聚类覆盖率,大幅减少费雪信息矩阵计算量,提升参数更新效率。其次,基于费雪信息矩阵,对模型参数更新过程中的损失函数增加2次惩罚项,限制MLP神经网络中重要权重与偏置参数的变化,在保持对原数据集检测性能的基础上,提升对新DDoS攻击数据集的检测准确率。然后基于概率论对EWC-UD方法进行正确性证明,并分析时间复杂度。实验表明,针对构建的测试数据集,EWC-UD方法相较于MLP-UD仅训练新DDoS攻击数据集的更新方法,检测准确率提升37.05%,相较于MLP-UD同时训练新旧DDoS攻击数据集的更新方法,时间开销下降80.65%,内存开销降低33.18%。Abstract: For the problem in the existing Multi-Layer Perceptron (MLP) based DDoS detection model parameter update method that the old model parameter training dataset knowledge is forgettable and the time and space complexity are enormous, a novel model parameter UpDate method EWC-UD based on Elastic Weight Consolidation (EWC) is proposed. Firstly, the cluster center points of the old dataset are calculated as the calculation samples of Fisher information matrix by the K-Means algorithm. The coverage rates of clusters and sampling uniformity are raised effectively, which significantly reduces the amount of Fisher Information Matrix calculation and improves the efficiency of the model parameter updates. Secondly, according to the calculated Fisher information matrix, a secondary penalty item is added to the loss function, limiting the important weight and bias parameter changes in the neural network. Maintaining the detection performance of the old DDoS attack dataset, EWC-UD improves the detection accuracy of the new DDoS attack datasets. Then based on probability theory, the correctness of EWC-UD is proved, and the time complexity is analyzed. Experiments show that for the constructed test dataset, the detection accuracy of EWC-UD is 37.05% higher than the MLP-UD that only trains the new DDoS attack dataset, and compared with the time MLP-UD training both new and old DDoS attack datasets, the time and memory costs are reduced by 80.65% and 33.18 respectively.
-
表 1 EWC-UD模型参数更新算法
输入:原数据集$ {D}_{A} $、新数据集$ {D}_{B} $ 输出:神经网络参数$ {\theta }^{*} $ 1: ${y_t} = {{\rm{label}}} \left( {{D_A}} \right)$ //获得数据集标签 2: $x = {\rm{data}}({D_A})$ //获得数据集数据 3: ${\rm{if} }$ $ {{\rm{Train}}} \_{\rm{Time}} = 1 $ ${\rm{then} }$//首次训练 4: ${{\rm{Var}}} \_{\rm{list}} = [{W_1},{b_1},{W_2},{b_2},{W_3},{b_3}]$ // 3层MLP神经网
络权重与偏置参数5: $N = {{\rm{len}}} ({D_A})$// 提取数据集长度 6: $ {y_p}(x) = {{\rm{MLP}}} \left( {x,{{\rm{Var}}} \_{\rm{list}}} \right) $// 神经网络输出预测结果 7: $L\left(\theta \right)=\mathrm{CrossEntropy}({y}_{t},{y}_{p})=\displaystyle\sum\nolimits_{{\rm{x}}}{y}_{t}(x)$
$\cdot \mathrm{lg}({y}_{p}(x))$// 设置损失函数8: ${\rm{Var\_list}} = {\rm{Grandient}}\;{\rm{Descent}}{\rm{.}}\;{\rm{minimize}}(L(\theta ))$//梯度
下降法搜寻最优参数9: ${\theta ^*} = {{\rm{Var}}} \_{\rm{list}}$ 10: ${\rm{End} } \;{\rm{if} }$ 11: ${\rm{else} }\; {\rm{if} }$ ${ {\rm{Train} } } \_{\rm{Time} } \ge 2$ ${\rm{then} }$//模型参数更新 12: ${{\rm{Var}}} \_{\rm{pre}} = {\rm{Var}}\_{\rm{List}}$//存储原模型参数 13: ${N_{\rm{Sample} } } = 30$//设置采样点数为30 14: $F = {\rm{zeros}}({\rm{Var}}\_{\rm{pre}})$//费雪信息矩阵初始化 15: ${\text{Sampl} }{ {\text{e} }_A} = { {\rm{K} } } \_{\rm{Means} }({D_A},{N_{\rm{Sample} } })$//利用K-Means算
法获得抽样点16: ${\rm{For} }$ $i$ ${\rm{in}}$ ${{\rm{range}}} ({\rm{len}}({{\rm{Sample}}_A}))$: //计算费雪信息矩
阵F17: ${{\rm{ders}}} = {{\rm{gradients}}} (\ln ({{{\rm{Sample}}} _A}[i]),{{\rm{Var}}} \_{\rm{pre}})$ 18: ${\rm{For} }$ $ v $ ${\rm{in}}$ ${{\rm{range}}} ({\rm{len}}(F))$: 19: $F[v] + = {{\rm{square}}} ({\rm{ders}}[v])$ 20: ${\rm{End} } \;{\rm{For} }$ 21: ${\rm{End} }\;{\rm{For} }$ 22: $ F = F/{{{\rm{Sample}}} _A} $ 23: ${\rm{End} } \;{\rm{if} }$ 24: ${\rm{For} }$ $i$ ${\rm{in}}$ ${{\rm{range}}} ({\rm{len}}({{\rm{Var}}} \_{\rm{List}}))$: // 修正损失函数 25: $L(\theta ) = { {\rm{Sum} } } ({ {\rm{CrossEntropy} } } ({y_t},{y_p}),{ {\rm{Multiply} } } (F\left[ v \right],$
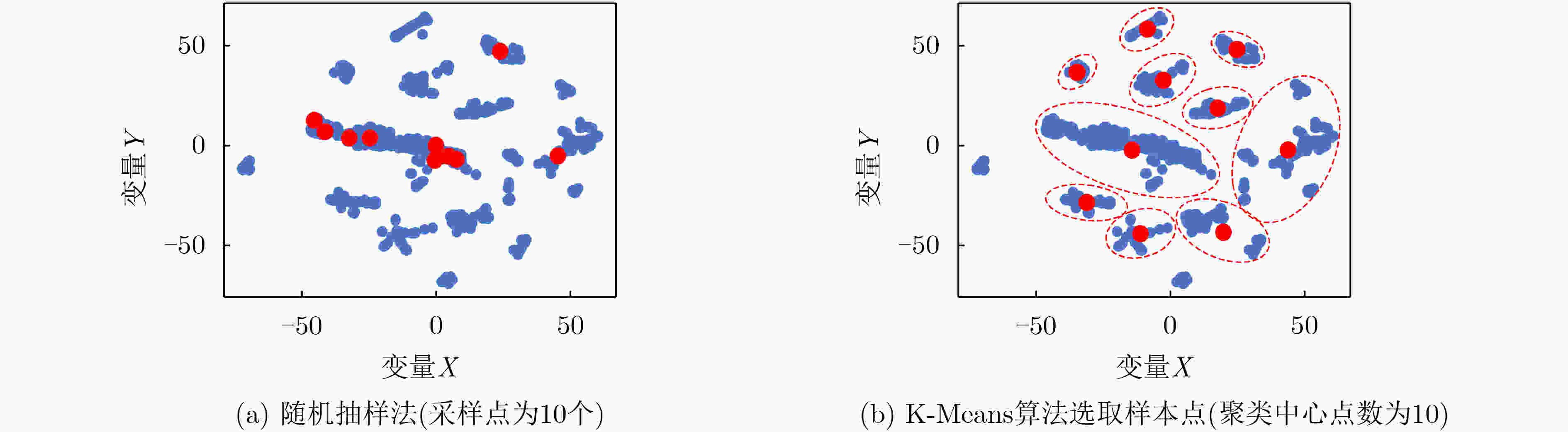
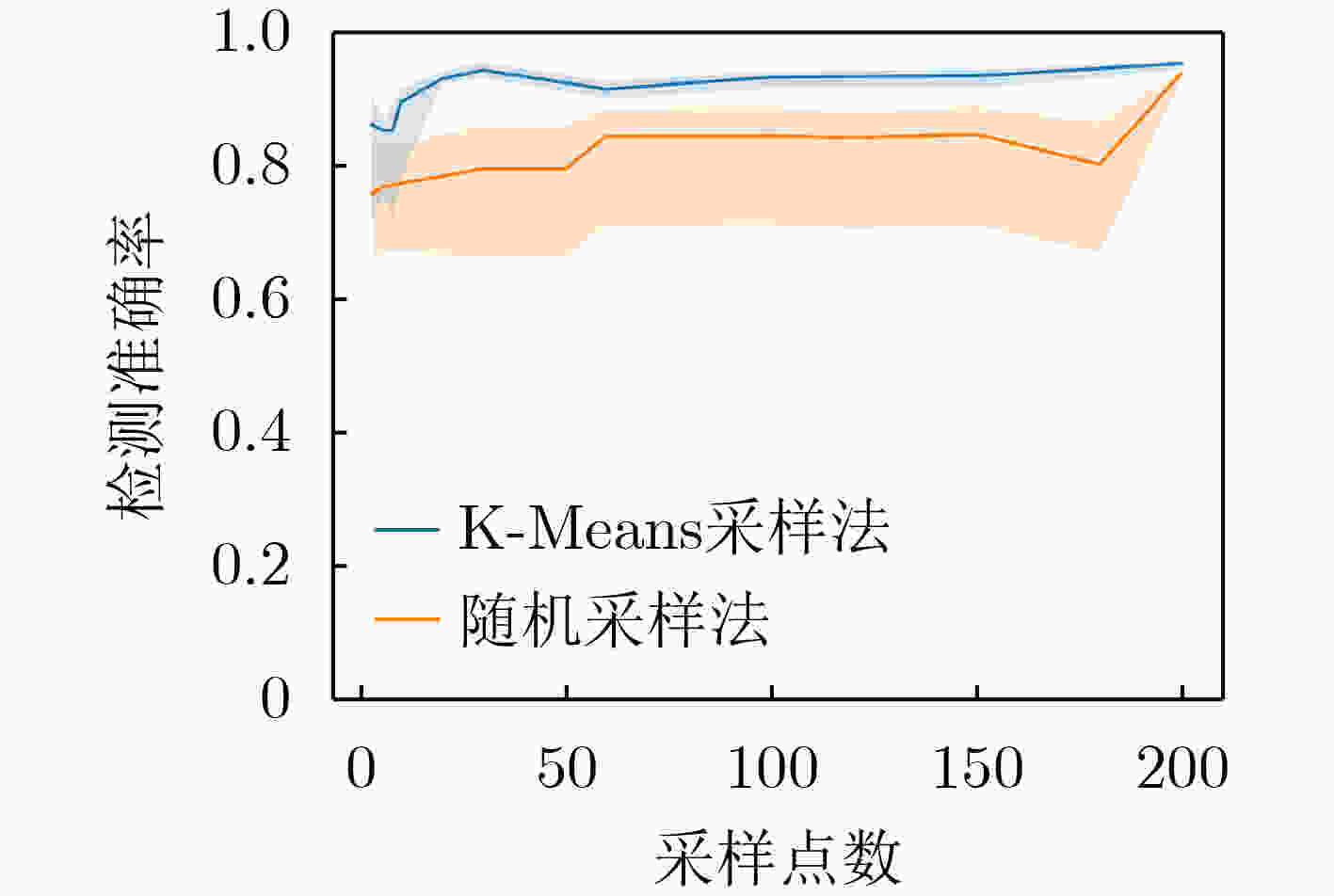
${(\theta [v] - { {\rm{Var} } } \_{\rm{pre} }[v])^2})) $26: ${\rm{End} } \;{\rm{For} }$ 27: ${\theta ^*} = { {\rm{Grandient\;Descent} } } .{\rm{minimize} }(L(\theta ))$ //输出网络参数 表 2 K-Means样本选取法与随机抽样法性能验证(%)
抽样样本数 平均准确率 最高准确率 最低准确率 K-Means Random K-Means Random K-Means Random 3 86.35 78.65 96.78 95.17 50.00 49.40 6 88.54 71.51 91.08 86.23 83.90 49.40 20 92.95 79.12 96.81 93.67 91.07 49.41 60 91.33 84.32 95.94 94.15 86.73 49.42 100 93.21 84.09 95.84 93.91 87.96 49.41 200 95.29 93.81 96.78 95.31 91.61 91.18 表 3 各类模型参数更新方法性能验证
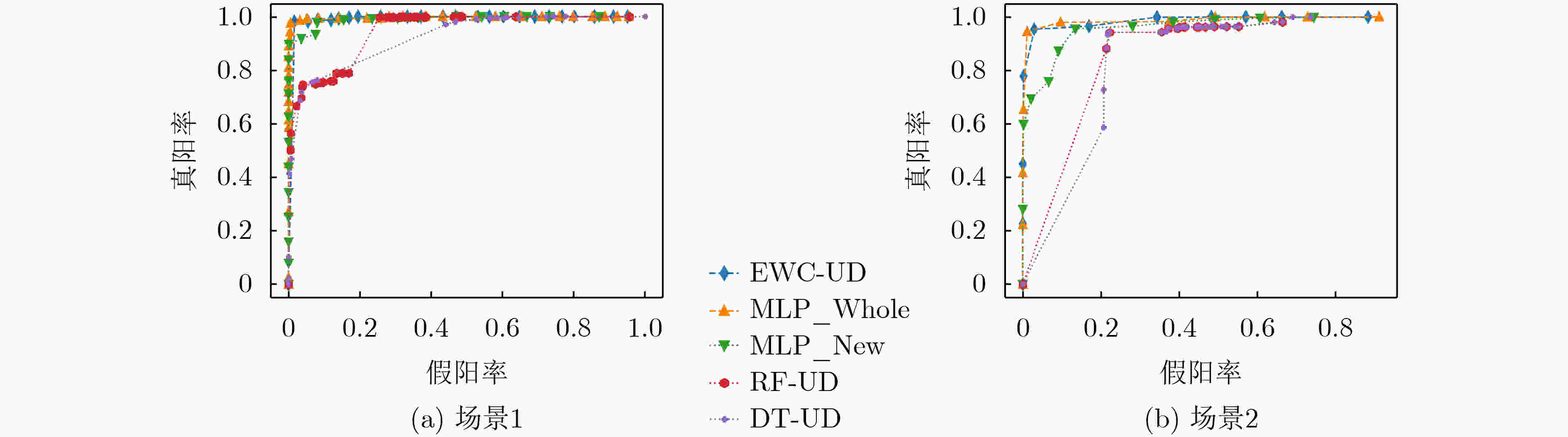
方法 场景1 场景2 准确率(%) 精准率(%) 召回率(%) F1分数 准确率(%) 精准率(%) 召回率(%) F1分数 MLP_Whole 98.41 97.93 98.98 0.98 97.12 94.10 97.12 0.96 MLP_New 88.71 97.09 71.72 0.83 59.52 99.17 44.94 0.62 RF-UD 88.50 71.73 90.31 0.80 73.57 94.47 55.98 0.70 DT-UD 89.13 74.63 89.61 0.81 87.85 95.09 74.93 0.84 EWC-UD 98.06 98.02 98.23 0.98 96.57 94.96 94.67 0.95 表 4 各类参数更新方法更新成本
方法 场景1 场景2 时间开销(s) 内存开销(MB) 时间开销(s) 内存开销(MB) MLP_Whole 753.53 12783.82 322.03 11259.08 MLP_New 182.28 7467.50 89.52 3195.62 RF-UD 127.40 6278.46 34.46 3850.60 DT-UD 125.53 7099.88 48.02 3743.80 EWC-UD 145.80 8541.24 128.18 4318.04 -
[1] WANG Meng, LU Yiqin, and QIN Jiancheng. A dynamic MLP-based DDoS attack detection method using feature selection and feedback[J]. Computers & Security, 2020, 88: 101645. doi: 10.1016/j.cose.2019.101645 [2] 董书琴, 张斌. 基于深度特征学习的网络流量异常检测方法[J]. 电子与信息学报, 2020, 42(3): 695–703. doi: 10.11999/JEIT190266DONG Shuqin and ZHANG Bin. Network traffic anomaly detection method based on deep features learning[J]. Journal of Electronics &Information Technology, 2020, 42(3): 695–703. doi: 10.11999/JEIT190266 [3] KEMKER R, MCCLURE M, ABITINO A, et al. Measuring catastrophic forgetting in neural networks[J]. arXiv preprint, arXiv: 1708.02072, 2017. [4] KUMARAN D, HASSABIS D, and MCCLELLAND J L. What learning systems do intelligent agents need? Complementary learning systems theory updated[J]. Trends in Cognitive Sciences, 2016, 20(7): 512–534. doi: 10.1016/j.tics.2016.05.004 [5] POLIKAR R, UPDA L, UPDA S S, et al. Learn++: An incremental learning algorithm for supervised neural networks[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) , 2001, 31(4): 497–508. doi: 10.1109/5326.983933 [6] ZRIBI M and BOUJELBENE Y. The neural networks with an incremental learning algorithm approach for mass classification in breast cancer[J]. Biomedical Data Mining, 2016, 5(118): 2. doi: 10.4172/2090-4924.1000118 [7] SHIOTANI S, FUKUDA T, and SHIBATA T. A neural network architecture for incremental learning[J]. Neurocomputing, 1995, 9(2): 111–130. doi: 10.1016/0925-2312(94)00061-V [8] GEPPERTH A and HAMMER B. Incremental learning algorithms and applications[C]. The 24th European Symposium on Artificial Neural Networks, Bruges, Belgium, 2016: 357–368. [9] MALLYA A, DAVIS D, and LAZEBNIK S. Piggyback: Adapting a single network to multiple tasks by learning to mask weights[C]. The 15th European Conference on Computer Vision, Munich, Germany, 2018: 72–88. doi: 10.1007/978-3-030-01225-0_5. [10] PÉREZ-SÁNCHEZ B, FONTENLA-ROMERO O, GUIJARRO-BERDIÑAS B, et al. An online learning algorithm for adaptable topologies of neural networks[J]. Expert Systems with Applications, 2013, 40(18): 7294–7304. doi: 10.1016/j.eswa.2013.06.066 [11] KIRKPATRICK J, PASCANU R, RABINOWITZ N, et al. Overcoming catastrophic forgetting in neural networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(13): 3521–3526. doi: 10.1073/pnas.1611835114 [12] CASTRO F M, MARÍN-JIMÉNEZ M J, GUIL N, et al. End-to-end incremental learning[C]. The 15th European Conference on Computer Vision, Munich, Germany, 2018: 241–257. doi: 10.1007/978-3-030-01258-8_15. [13] Canadian Institute for Cybersecurity. CIC-DoS-2016[EB/OL]. https://www.unb.ca/cic/datasets/dos-dataset.html, 2020. [14] Canadian Institute for Cybersecurity. CES-DDoS-2017[EB/OL]. https://www.unb.ca/cic/datasets/ids-2017.html, 2020. [15] Canadian Institute for Cybersecurity. CES-CIC-IDS2018-AWS[EB/OL]. https://www.unb.ca/cic/datasets/ids-2018.html, 2020. [16] SHARAFALDIN I, LASHKARI A H, HAKAK S, et al. Developing realistic distributed denial of service (DDoS) attack dataset and taxonomy[C]. 2019 International Carnahan Conference on Security Technology, Chennai, India, 2019: 1–8. doi: 10.1109/CCST.2019.8888419. -





 下载:
下载:


 下载:
下载:
