基于树形奇偶机的密钥交换优化方案

韩益亮; 李鱼; 李喆

doi:10.11999/JEIT200633

基于树形奇偶机的密钥交换优化方案

doi: 10.11999/JEIT200633

武警工程大学密码工程学院西安 710086

基金项目: 国家自然科学基金(61572521)，武警工程大学科研创新团队科学基金(KYTD201805)，陕西省自然科学基础研究计划(2021-JM252)

详细信息

作者简介:
韩益亮：男，1977年生，博士，教授，研究方向为信息安全、神经密码学

李鱼：男，1995年生，硕士生，研究方向为神经密码学

李喆：男，1994年生，硕士生，研究方向为神经密码学

通讯作者:
韩益亮　hanyil@163.com

中图分类号: TN918; TP309.7
计量
- 文章访问数: 1012
- HTML全文浏览量: 556
- PDF下载量: 118
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-29
- 修回日期: 2020-12-25
- 网络出版日期: 2020-12-31
- 刊出日期: 2021-08-10

A Key Exchange Optimization Scheme Based on Tree Parity Machine

Department of Cryptographic Engineering, Engineering University of PAP, Xi’an 710086, China

Funds: The National Natural Science Foundation of China (61572521), The Scientific Foundation of the Scientific Research and Innovation Team of Engineering University of PAP (KYTD201805), The Natural Science Basic Research Plan in Shaanxi Province (2021JM252)

摘要

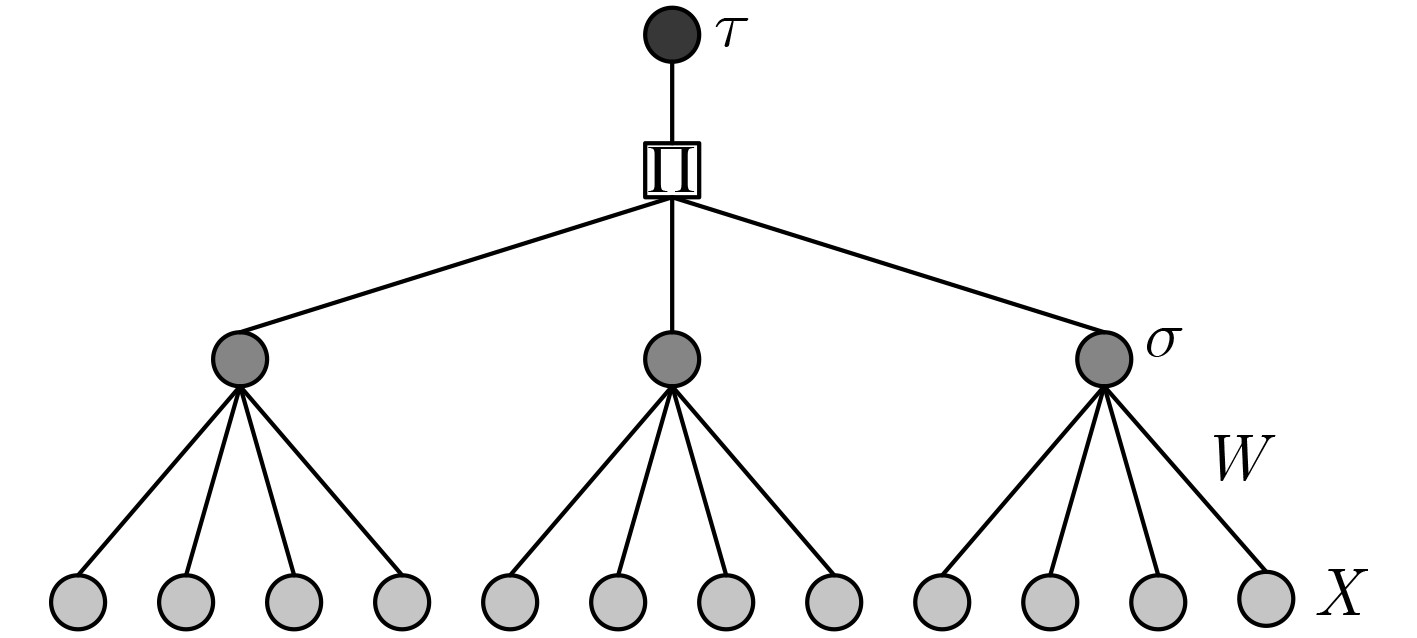
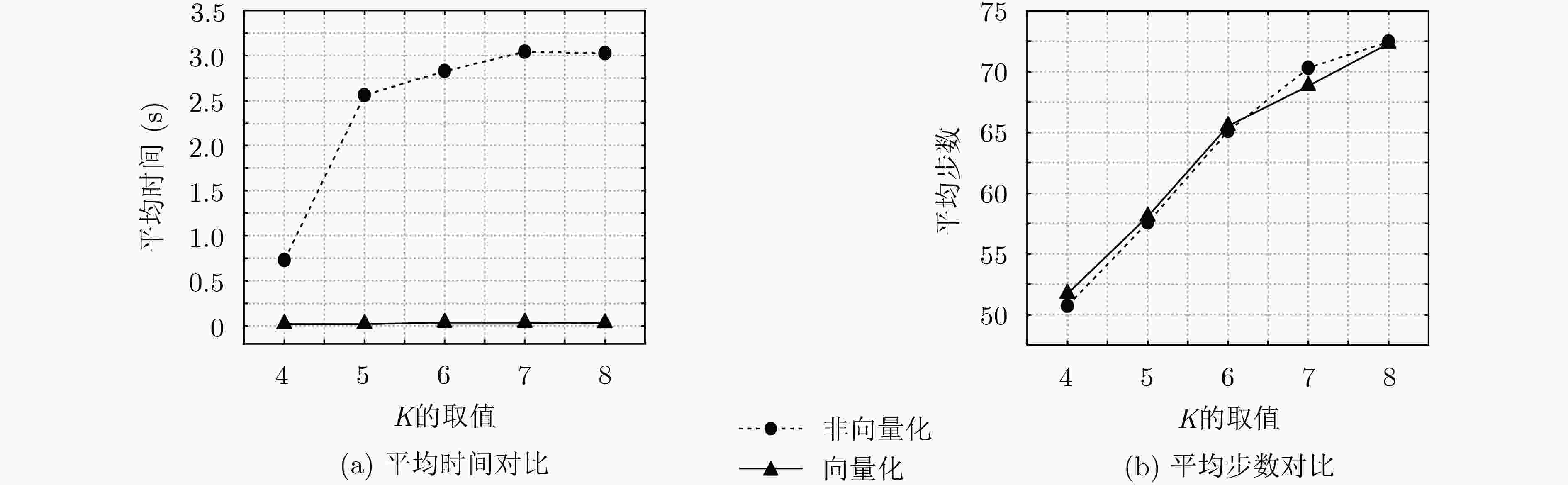
摘要: 树形奇偶机(TPM)之间的相互同步学习能够用于实现密钥交换方案，方案的安全性取决于树形奇偶机的结构参数。为了得到使得密钥交换方案安全性高且计算量小的参数，该文提出基于树形奇偶机的密钥交换优化方案。首先，定义向量化的学习规则，提高树形奇偶机同步学习的时间效率。其次，改进针对树形奇偶机同步学习的合作攻击算法，使其能够自适应参数的变化。最后，通过仿真实验对方案进行了效率和安全性测试。实验结果表明，树形奇偶机的向量化能使同步时间减少约90%，但不会减少同步所需的步数，即不影响方案的安全性。在可用于生成512 bit固定长度密钥的结构参数中，(14, 14, 2)被合作攻击攻破的概率为0%，所需同步时间较少。因此，所提密钥交换优化方案是安全高效的。
- 密码学 /
- 密钥交换 /
- 人工神经网络 /
- 树形奇偶机 /
- 相互学习
Abstract: Synchronization of Tree Parity Machines (TPM) by mutual learning can be used to achieve key exchange schemes. The security of the scheme depends on the structure parameters of TPM. In order to obtain the parameters that make the key exchange scheme more secure and less computation, a key exchange optimization scheme based on TPM is proposed. Firstly, the learning rules of vectorization are defined to improve the efficiency of synchronization of TPM. Secondly, the cooperating attack algorithm for synchronization of TPM is improved to make it adaptive to the change of parameters. Finally, the efficiency and security of the scheme are tested by simulation experiment. The simulation results show that the vectorization of TPM can reduce the synchronization time by about 90%, which does not reduce the number of steps required for synchronization and affect the security. Among the parameters that can be used to generate 512 bit fixed length key, the probability of (14, 14, 2) being attacked by cooperating attack is 0%, and the synchronization time is less. Therefore, the proposed key exchange optimization scheme is secure and efficient.
- Cryptography /
- Key exchange /
- Artificial neural network /
- Tree Parity Machine(TPM) /
- Mutual learning

HTML全文

图 1 K=3和N=4的树形奇偶机

下载: 全尺寸图片幻灯片

图 2 K和N同时变化对攻击成功率的影响

下载: 全尺寸图片幻灯片

图 3 单一参数变化对攻击成功率的影响

下载: 全尺寸图片幻灯片

图 4 向量化与非向量化的对比

下载: 全尺寸图片幻灯片

表 1 变量说明

变量	描述
K	隐藏层神经元数量
N	输入神经元数量
L	神经元权重所能取的最大值
L_BIN	L的二进制值的比特长度
average_steps	平均每次神经密钥交换所需的同步步数
average_time	平均每次神经密钥交换所需的同步时间
X	随机输入向量
tauA	Alice的vTPM的输出
tauE	攻击者Eve的vTPM的输出
M	合作攻击者的数量
Steps	同步的步数
P_Geometric	几何攻击的成功概率
P_Cooperating	合作攻击的成功概率

下载: 导出CSV

表 2 参数组合

K	N	L_BIN	L
4	64	2	1
4	43	3	2或3
4	32	4	4或5或6或7
5	52	2	1
5	35	3	2或3
5	26	4	4
6	43	2	1
6	29	3	2或3
6	22	4	4
7	37	2	1
7	25	3	2或3
8	28	2	1
8	19	3	2或3
9	29	2	1
9	19	3	2或3
10	26	2	1
10	18	3	2或3
11	24	2	1
11	16	3	2或3
12	22	2	1
12	15	3	2或3
13	20	2	1
13	14	3	2或3
14	19	2	1
14	14	3	2或3

下载: 导出CSV

表 3 效率测试算法(算法1)

输入：K, N, L
输出：average_steps, average_time
(1) total_steps, total_time ← 0
(2) FOR i ←0 TO s DO
(3) 　　Alice 用参数K,N,L初始化树形奇偶机
(4) 　　Bob 用参数K,N,L初始化树形奇偶机
(5) 　　steps ← 0
(6) 　　将当前时间赋值给start_time
(7) 　　WHILE 没有达到同步状态 DO
(8) 　　　　生成随机输入向量${\boldsymbol{X}}$
(9) 　　　　Alice 用${\boldsymbol{X}}$计算自己的输出结果
(10) 　　　　Bob用${\boldsymbol{X}}$计算自己的输出结果
(11) 　　　　　IF tauA == tauB THEN
(12) 　　　　　　Alice根据指定学习规则更新权值
(13) 　　　　　　Bob 根据指定学习规则更新权值
(14) 　　　　　steps ← steps + 1
(15) 　　　　将当前时间赋值给end_time ← current time
(16) 　　　　计算每次同步时间each_time ← end_time – 　　　　　　　 start_time
(17) 　　　　更新总步数total_steps ← total_steps + steps
(18) 　　　　更新总时间total_time ← total_time + 　　　　　　　 each_time
(19) 计算平均同步步数average_steps ← total_steps/s
(20) 计算平均同步时间average_time ← total_time/s
(21) END

下载: 导出CSV

表 4 安全性测试算法(算法2)

输入：tauA, tauE, Eve, m, steps, average_steps
输出：P_Cooperating
(1) IF steps % 2 == 0 and steps >= average_steps/3 THEN
(2) 　　FOR i ← 0 TO m DO
(3) 　　　IF tauA!= tauE[i] THEN
(4) 　　　　Eve[i] 更新隐藏层输出
(5) 　　选择出现次数最多的隐藏层输出
(6) 　　FOR i ← 0 TO m DO
(7) 　　　将出现次数最多的隐藏层输出赋值给Eve[i]
(8) 　　　Eve[i]根据学习规则更新权值
(9) ELSE
(10) 　　　FOR i ← 0 TO m DO
(11) 　　　　IF tauA == tauE THEN
(12) 　　　　　Eve[i]根据学习规则更新权值
(13) 　　　　ELSE
(14) 　　　　　Eve[i] 更新隐藏层输出
(15) 　　　　　Eve[i] 根据学习规则更新权值
(16) END

下载: 导出CSV

表 5 向量化方法对比

方案	向量化方法	适用编程语言	优化参数	安全性测试
文献[16]	NumPy库	Python	—	—
本文	定义向量化学习规则	不限	(14, 14, 2)	√

下载: 导出CSV

表 6 仿真结果(1000次)

(K, N, L)	平均步数	平均时间(s)	几何攻击成功率(%)	合作攻击成功率(%)	(K, N, L)	平均步数	平均时间(s)	几何攻击成功率(%)	合作攻击成功率(%)
(4, 64, 1)	51.742	0.0192	34.4	99.1	(9, 19, 2)	333.006	0.1527	0	0.1
(4, 43, 2)	179.083	0.0606	17.4	51.9	(9, 19, 3)	1218.468	0.6346	–	–
(4, 43, 3)	456.675	0.6967	7.1	28.4	(10, 26, 1)	78.488	0.0600	6.8	74.4
(4, 32, 4)	870.972	0.3276	3.9	19.8	(10, 18, 2)	359.298	0.3080	0	0.2
(4, 32, 5)	1493.557	0.4359	1.7	14.8	(10, 18, 3)	1297.029	0.6672	–	–
(4, 32, 6)	2325.563	1.2867	–	–	(11, 24, 1)	80.759	0.0849	4.0	67.4%
(5, 52, 1)	58.071	0.0208	28.1	97.8	(11, 16, 2)	369.292	0.2557	0	0
(5, 35, 2)	228.839	0.0985	6.1	22.3	(11, 16, 3)	1296.374	0.4165	0	0
(5, 35, 3)	696.446	0.2577	0.6	6.4	(11, 12, 4)	2676.733	0.7485	–	–
(5, 26, 4)	1661.632	1.2144	–	–	(12, 22, 1)	83.801	0.0415	4.0	64.6
(6, 43, 1)	65.541	0.0327	19.5	94.6	(12, 15, 2)	382.903	0.1292	0	0
(6, 29, 2)	280.347	0.2733	2.6	8.1	(12, 15, 3)	1265.186	0.3841	0	0
(6, 29, 3)	950.247	0.7407	–	–	(12, 12, 4)	2886.052	0.8301	–	–
(7, 37, 1)	68.821	0.0344	14.0	93.6	(13, 20, 1)	84.482	0.0270	3.7	60.2
(7, 25, 2)	303.197	0.2187	0.7	1.9	(13, 14, 2)	381.464	0.1429	0	0
(7, 25, 3)	1117.517	1.0476	–	–	(13, 14, 3)	1281.136	0.5002	–	–
(8, 32, 1)	72.327	0.0303	9.9	85.9	(14, 19, 1)	86.002	0.0602	2.6	58.6
(8, 22, 2)	328.483	0.1181	0.2	0.6	(14, 14, 2)	388.856	0.1219	0	0
(8, 22, 3)	1197.173	0.8345	–	–	(14, 14, 3)	1380.606	0.6708	–	–
(9, 29, 1)	76.621	0.0801	7.7	82.7

下载: 导出CSV

表 7 效率对比

方案	密钥长度(bit)	平均时间(ms)
文献[17]	512	92.1294
文献[18]	256	11.9198
文献[22]	512	235.4931
本文	512	6.0496

下载: 导出CSV

参考文献(22)

[1]	蒋瀚, 刘怡然, 宋祥福, 等. 隐私保护机器学习的密码学方法[J]. 电子与信息学报, 2020, 42(5): 1068–1078. doi: 10.11999/JEIT190887 JIANG Han, LIU Yiran, SONG Xiangfu, et al. Cryptographic approaches for privacy-preserving machine learning[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1068–1078. doi: 10.11999/JEIT190887
[2]	ALANI M M. Applications of machine learning in cryptography: A survey[C]. The 3rd International Conference on Cryptography, Security and Privacy, Kuala Lumpur, Malaysia, 2019: 23–27.
[3]	KANTER I, KINZEL W, and KANTER E. Secure exchange of information by synchronization of neural networks[J]. Europhysics Letters, 2002, 57(1): 141–147. doi: 10.1209/epl/i2002-00552-9
[4]	KINZEL W and KANTER I. Interacting Neural Networks and Cryptography[M]. KRAMER B. Advances in Solid State Physics. Berlin: Springer, 2002: 383–391.
[5]	KLIMOV A, MITYAGIN A, and SHAMIR A. Analysis of neural cryptography[C]. The 8th International Conference on the Theory and Application of Cryptology and Information Security, Queenstown, New Zealand, 2002: 288–298.
[6]	SHACHAM L N, KLEIN E, MISLOVATY R, et al. Cooperating attackers in neural cryptography[J]. Physical Review E, 2004, 69(6): 066137. doi: 10.1103/PhysRevE.69.066137
[7]	RUTTOR A, KINZEL W, and KANTER I. Neural cryptography with queries[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2005: P01009. doi: 10.1088/1742-5468/2005/01/P01009
[8]	ALLAM A M, ABBAS H M, and EL-KHARASHI M W. Authenticated key exchange protocol using neural cryptography with secret boundaries[C]. 2013 International Joint Conference on Neural Networks, Dallas, USA, 2013: 1–8.
[9]	PAL S K and MISHRA S. An TPM based approach for generation of secret key[J]. International Journal of Computer Network and Information Security, 2019, 11(10): 45–50. doi: 10.5815/ijcnis.2019.10.06
[10]	DONG Tao and HUANG Tingwen. Neural cryptography based on complex-valued neural network[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(11): 4999–5004. doi: 10.1109/TNNLS.2019.2955165
[11]	SARKAR A. Multilayer neural network synchronized secured session key based encryption in wireless communication[J]. IAES International Journal of Artificial Intelligence, 2019, 8(1): 44–53. doi: 10.11591/ijai.v8.i1.pp44-53
[12]	SARKAR A, DEY J, KARFORMA S, et al. Notice of retraction coupled tree parity machines: Synchronized secured session key based encryption in online transaction[J]. Aptikom Journal on Computer Science and Information Technologies, 2019, 4(1): 27–36. doi: 10.11591/APTIKOM.J.CSIT.133
[13]	肖成龙, 孙颖, 林邦姜, 等. 基于神经网络与复合离散混沌系统的双重加密方法[J]. 电子与信息学报, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213 XIAO Chenglong, SUN Ying, LIN Bangjiang, et al. Double encryption method based on neural network and composite discrete chaotic system[J]. Journal of Electronics &Information Technology, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213
[14]	SABALLUS B, VOLKMER M, and WALLNER S. Secure group communication in Ad-Hoc networks using tree parity machines[C]. Communication in Distributed Systems-15. ITG/GI Symposium, Bern, Switzerland, 2007: 1–12.
[15]	SANTHANALAKSHMI S, SANGEETA K, and PATRA G K. Design of group key agreement protocol using neural key synchronization[J]. Journal of Interdisciplinary Mathematics, 2020, 23(2): 435–451. doi: 10.1080/09720502.2020.1731956
[16]	CHOURASIA S, CHAKRAPANI H B, DAS Q, et al. Vectorized neural key exchange using tree parity machine[J]. Compusoft: An International Journal of Advanced Computer Technology, 2019, 8(5): 3140–3145.
[17]	WALTER É S, FUERTES W, and LASCANO E. On the development of an optimal structure of tree parity machine for the establishment of a cryptographic key[J]. Security and Communication Networks, 2019, 2019: 8214681. doi: 10.1155/2019/8214681
[18]	BOS J, COSTELLO C J, DUCAS L, et al. Frodo: Take off the ring! Practical, quantum-secure key exchange from LWE[C]. The 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 2016: 1006–1018.
[19]	RUTTOR A. Neural synchronization and cryptography[D]. [Ph.D. dissertation], Universität Würzburg, 2006.
[20]	MISLOVATY R, PERCHENOK Y, KANTER I, et al. Secure key-exchange protocol with an absence of injective functions[J]. Physical Review E, 2002, 66(6): 066102. doi: 10.1103/PhysRevE.66.066102
[21]	KINZEL W. Theory of Interacting Neural Networks[M]. BORNHOLDT S and SCHUSTER H G. Handbook of Graphs and Networks: From the Genome to the Internet. Weinheim, Germany, Wiley, 2003: 199–220.
[22]	DANIEL R M, RAJSINGH E B, and SILAS S. An efficient eCK secure identity based Two Party Authenticated Key Agreement scheme with security against active adversaries[J]. Information and Computation, 2020, 275: 104630. doi: 10.1016/j.ic.2020.104630