Modeling of Network Attack and Defense Behavior and Analysis of Situation Evolution Based on Game Theory
-
摘要: 网络安全本质在对抗。针对现有研究缺乏从博弈视角分析网络攻防行为与态势演化关系的问题,该文提出一种网络攻防博弈架构模型(NADGM),借鉴传染病动力学理论以不同安全状态网络节点密度定义网络攻防态势,分析网络节点安全状态转移路径;以网络勒索病毒攻防博弈为例,使用NetLogo多Agent仿真工具开展不同场景下攻防态势演化趋势对比实验,得出增强网络防御效能的结论。实验结果验证了模型方法的有效性和可行性。Abstract: The essence of network security is confrontation. In view of at the problem that the existing research lacks to analyze the relationship between network attack and defense behavior and situation evolution from the perspective of game, a Network Attack And Defense Game architecture Model (NADGM) is proposed, the theory of infectious disease dynamics is used to define the network attack and defense situation with the density of network nodes in different security states, and the network node security state transition path is analyzed; The network blackmail virus attack and defense game is taken as an example, and NetLogo multi-agent simulation tools is used to carry out comparative experiments of attack and defense situation evolution trend in different scenarios, and the conclusion of enhancing network defense effectiveness is obtained. The experimental results verify the effectiveness and feasibility of the model method.
-
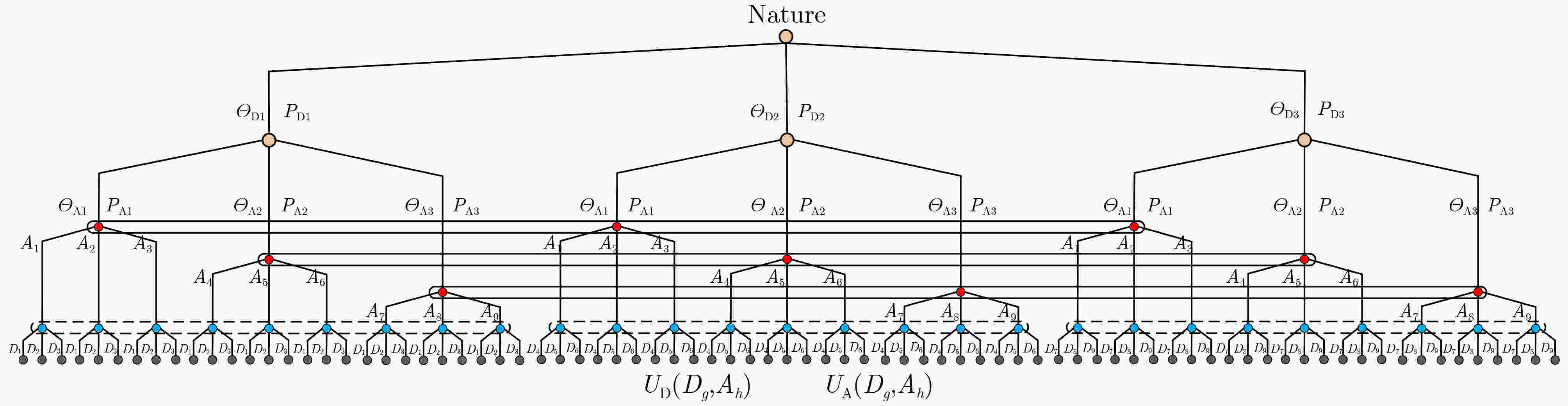
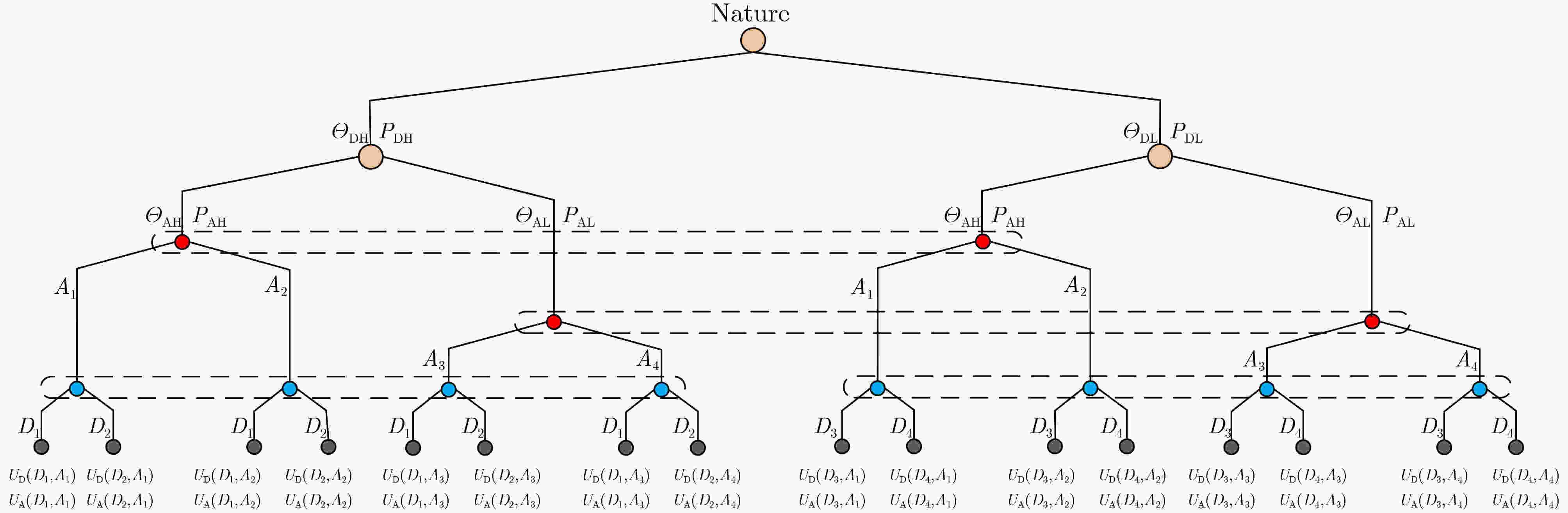
表 1 勒索病毒攻防类型及策略划分
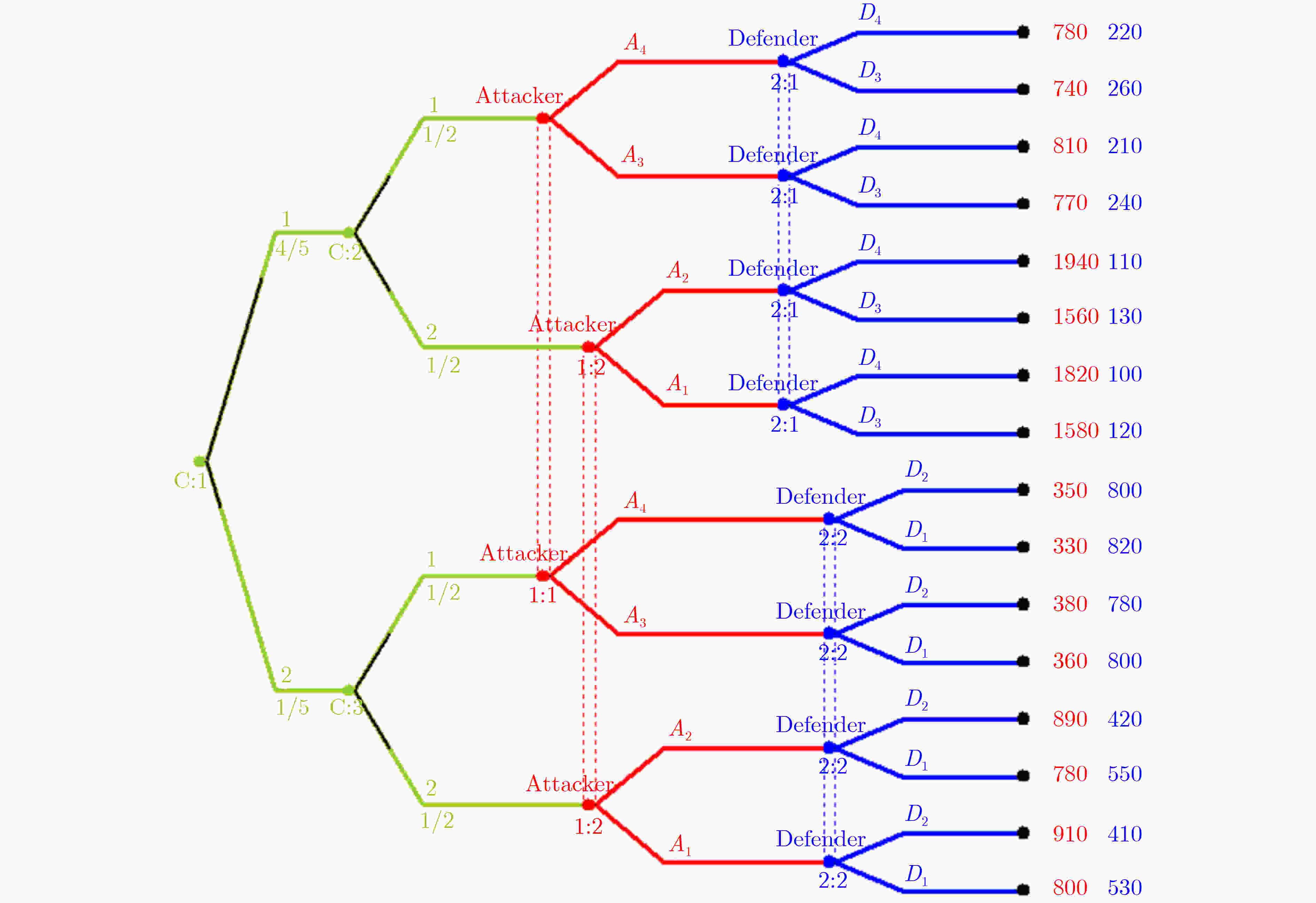
攻防类型 攻防策略 策略含义 ${\varTheta _{ {\rm{DH} } } }$ D1 安全意识强,及时升级系统和病毒库等 D2 安全意识强,及时修补漏洞等 ${\varTheta _{ {\rm{DL} } } }$ D3 安全意识弱,延迟升级系统和病毒库等 D4 安全意识弱,延迟修补漏洞等 ${\varTheta _{ {\rm{AH} } } }$ A1 攻击能力强,熟练运用漏洞扫描攻击等 A2 攻击能力强,熟练运用社会工程学攻击等 ${\varTheta _{ {\rm{AL} } } }$ A3 攻击能力弱,勉强运用漏洞扫描攻击等 A4 攻击能力弱,勉强运用社会工程学攻击等 表 2 不同策略组合下攻防收益
防御策略 攻击策略 A1 A2 A3 A4 D1 (530,800) (550,780) (800,360) (820,330) D2 (410,910) (420,890) (780,380) (800,350) D3 (120,1580) (130,1560) (240,770) (260,740) D4 (100,1820) (110,1940) (210,810) (220,780) -
[1] 屈蕾蕾, 肖若瑾, 石文昌, 等. 涌现视角下的网络空间安全挑战[J]. 计算机研究与发展, 2020, 57(4): 803–823. doi: 10.7544/issn1000-1239.2020.20190379QU Leilei, XIAO Ruojin, SHI Wenchang, et al. Cybersecurity challenges from the perspective of emergence[J]. Journal of Computer Research and Development, 2020, 57(4): 803–823. doi: 10.7544/issn1000-1239.2020.20190379 [2] LIU Xiaohu, ZHANG Hengwei, ZHANG Yuchen, et al. Optimal network defense strategy selection method based on evolutionary network game[J]. Security and Communication Networks, 2020, 2020: 5381495. doi: 10.1155/2020/5381495 [3] TAN Jinglei, LEI Cheng, ZHANG Hongqi, et al. Optimal strategy selection approach to moving target defense based on Markov robust game[J]. Computers & Security, 2019, 85: 63–76. doi: 10.1016/J.COSE.2019.04.013 [4] 张焕国, 杜瑞颖. 网络空间安全学科简论[J]. 网络与信息安全学报, 2019, 5(3): 4–18. doi: 10.11959/j.issn.2096-109x.2019021ZHANG Huanguo and DU Ruiying. Introduction to cyberspace security discipline[J]. Chinese Journal of Network and Information Security, 2019, 5(3): 4–18. doi: 10.11959/j.issn.2096-109x.2019021 [5] PAWLICK J, COLBERT E, and ZHU Quanyan. A game-theoretic taxonomy and survey of defensive deception for cybersecurity and privacy[J]. ACM Computing Surveys, 2019, 52(4): 82. doi: 10.1145/3337772 [6] 徐瑨, 吴慧慈, 陶小峰. 5G网络空间安全对抗博弈[J]. 电子与信息学报, 2020, 42(10): 2319–2329. doi: 10.11999/JEIT200058XU Jin, WU Huici, and TAO Xiaofeng. 5G cyberspace security game[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2319–2329. doi: 10.11999/JEIT200058 [7] 姜伟, 方滨兴, 田志宏, 等. 基于攻防博弈模型的网络安全测评和最优主动防御[J]. 计算机学报, 2009, 32(4): 817–827. doi: 10.3724/SP.J.1016.2009.00817JIANG Wei, FANG Binxing, TIAN Zhihong, et al. Evaluating network security and optimal active defense based on attack-defense game model[J]. Chinese Journal of Computers, 2009, 32(4): 817–827. doi: 10.3724/SP.J.1016.2009.00817 [8] 王增光, 卢昱, 李玺. 基于攻防博弈的军事信息网络安全风险评估[J]. 军事运筹与系统工程, 2019, 33(2): 35–40, 47. doi: 10.3969/j.issn.1672-8211.2019.02.007WANG Zengguang, LU Yu, and LI Xi. Risk assessment of military information network security based on attack defense game[J]. Military Operations Research and Systems Engineering, 2019, 33(2): 35–40, 47. doi: 10.3969/j.issn.1672-8211.2019.02.007 [9] 王晋东, 余定坤, 张恒巍, 等. 基于不完全信息攻防博弈的最优防御策略选取方法[J]. 小型微型计算机系统, 2015, 36(10): 2345–2348. doi: 10.3969/j.issn.1000-1220.2015.10.033WANG Jindong, YU Dingkun, ZHANG Hengwei, et al. Defense strategies selection based on incomplete information attack-defense game[J]. Journal of Chinese Computer Systems, 2015, 36(10): 2345–2348. doi: 10.3969/j.issn.1000-1220.2015.10.033 [10] 王晋东, 余定坤, 张恒巍, 等. 静态贝叶斯博弈主动防御策略选取方法[J]. 西安电子科技大学学报: 自然科学版, 2016, 43(1): 144–150. doi: 10.3969/j.issn.1001-2400.2016.01.026WANG Jindong, YU Dingkun, ZHANG Hengwei, et al. Active defense strategy selection based on the static Bayesian game[J]. Journal of Xidian University, 2016, 43(1): 144–150. doi: 10.3969/j.issn.1001-2400.2016.01.026 [11] 张烙兵, 阮启明, 邱晓刚. 研究社会复杂系统的两种互补方法: 仿真与博弈论[J]. 系统仿真学报, 2019, 31(10): 1960–1969. doi: 10.16182/j.issn1004731x.joss.19-0513ZHANG Laobing, RUAN Qiming, and QIU Xiaogang. Two complementary methods for studying complex social systems: Simulation and game theory[J]. Journal of System Simulation, 2019, 31(10): 1960–1969. doi: 10.16182/j.issn1004731x.joss.19-0513 [12] 刘小虎, 张恒巍, 张玉臣, 等. 基于博弈模型与NetLogo仿真的网络攻防态势研究[J]. 系统仿真学报, 2020, 32(10): 1918–1926. doi: 10.16182/j.issn1004731x.joss.20-fz0290LIU Xiaohu, ZHANG Hengwei, ZHANG Yuchen, et al. Research on network attack and defense situation based on game theory model and NetLogo simulation[J]. Journal of System Simulation, 2020, 32(10): 1918–1926. doi: 10.16182/j.issn1004731x.joss.20-fz0290 [13] LIU Xiaohu, ZHANG Hengwei, ZHANG Yuchen, et al. Active defense strategy selection method based on two-way signaling game[J]. Security and Communication Networks, 2019, 2019: 1362964. doi: 10.1155/2019/1362964 [14] 谭晶磊, 张恒巍, 张红旗, 等. 基于Markov时间博弈的移动目标防御最优策略选取方法[J]. 通信学报, 2020, 41(1): 42–52. doi: 10.11959/j.issn.1000-436x.2020003TAN Jinglei, ZHANG Hengwei, ZHANG Hongqi, et al. Optimal strategy selection approach of moving target defense based on Markov time game[J]. Journal on Communications, 2020, 41(1): 42–52. doi: 10.11959/j.issn.1000-436x.2020003 [15] 姜伟, 方滨兴, 田志宏, 等. 基于攻防随机博弈模型的防御策略选取研究[J]. 计算机研究与发展, 2010, 47(10): 1714–1723.JIANG Wei, FANG Binxing, TIAN Zhihong, et al. Research on defense strategies selection based on attack-defense stochastic game model[J]. Journal of Computer Research and Development, 2010, 47(10): 1714–1723. [16] FUDENBERG D and TIROLE J. Game Theory[M]. Boston: Massachusetts Institute of Technology Press, 2019. [17] ZHANG Hengwei, YU Dingkun, WANG Jindong, et al. Security defence policy selection method using the incomplete information game model[J]. China Communications, 2015(S2): 123–131. [18] MCKELVEY R D, MCLENNAN A M, and TUROCY T L. Gambit: Software tools for game theory, version 16.0. 1[EB/OL]. http://www.gambit-project.org, 2016. [19] HUSTED N and MYERS S. Emergent properties & security: The complexity of security as a science[C]. Proceedings of the 2014 New Security Paradigms Workshop, Victoria, 2014: 1–14. doi: 10.1145/2683467.2683468. [20] SHASHIDHAR N, KARI C, and VERMA R. The efficacy of epidemic algorithms on detecting node replicas in wireless sensor networks[J]. Journal of Sensor and Actuator Networks, 2015, 4(4): 378–409. doi: 10.3390/jsan4040378 [21] 孟庆微, 仇铭阳, 王刚, 等. 零日病毒传播模型及稳定性分析[J]. 电子与信息学报, 2021, 43(7): 1849–1855. doi: 10.11999/JEIT200519MENG Qingwei, QIU Mingyang, WANG Gang, et al. Zero-day virus transmission model and stability analysis[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1849–1855. doi: 10.11999/JEIT200519 [22] ZHANG Hengwei, JIANG Lv, HUANG Shirui, et al. Attack-defense differential game model for network defense strategy selection[J]. IEEE Access, 2018, 7: 50618–50629. doi: 10.1109/ACCESS.2018.2880214 [23] 张恒巍, 李涛, 黄世锐. 基于攻防微分博弈的网络安全防御决策方法[J]. 电子学报, 2018, 46(6): 1428–1435. doi: 10.3969/j.issn.0372-2112.2018.06.023ZHANG Hengwei, LI Tao, and HUANG Shirui. Network defense decision-making method based on attack-defense differential game[J]. Acta Electronica Sinica, 2018, 46(6): 1428–1435. doi: 10.3969/j.issn.0372-2112.2018.06.023 [24] VARGAS-DE-LEÓN C. On the global stability of SIS, SIR and SIRS epidemic models with standard incidence[J]. Chaos, Solitons & Fractals, 2011, 44(12): 1106–1110. doi: 10.1016/j.chaos.2011.09.002 [25] SHARMEEN S, AHMED Y A, HUDA S, et al. Avoiding future digital extortion through robust protection against ransomware threats using deep learning based adaptive approaches[J]. IEEE Access, 2020, 8: 24522–24534. doi: 10.1109/ACCESS.2020.2970466 [26] GORDON L, LOEB M, LUCYSHYN W, et al. 2015 CSI/FBI computer crime and security survey[C]. The Computer Security Institute, San Francisco, USA, 2015: 48–64. [27] TISUE S and WILENSKY U. NetLogo: A simple environment for modeling complexity[C]. The 5th International Conference on Complex Systems, Trieste, Italy, 2004: 16–21. -





 下载:
下载:

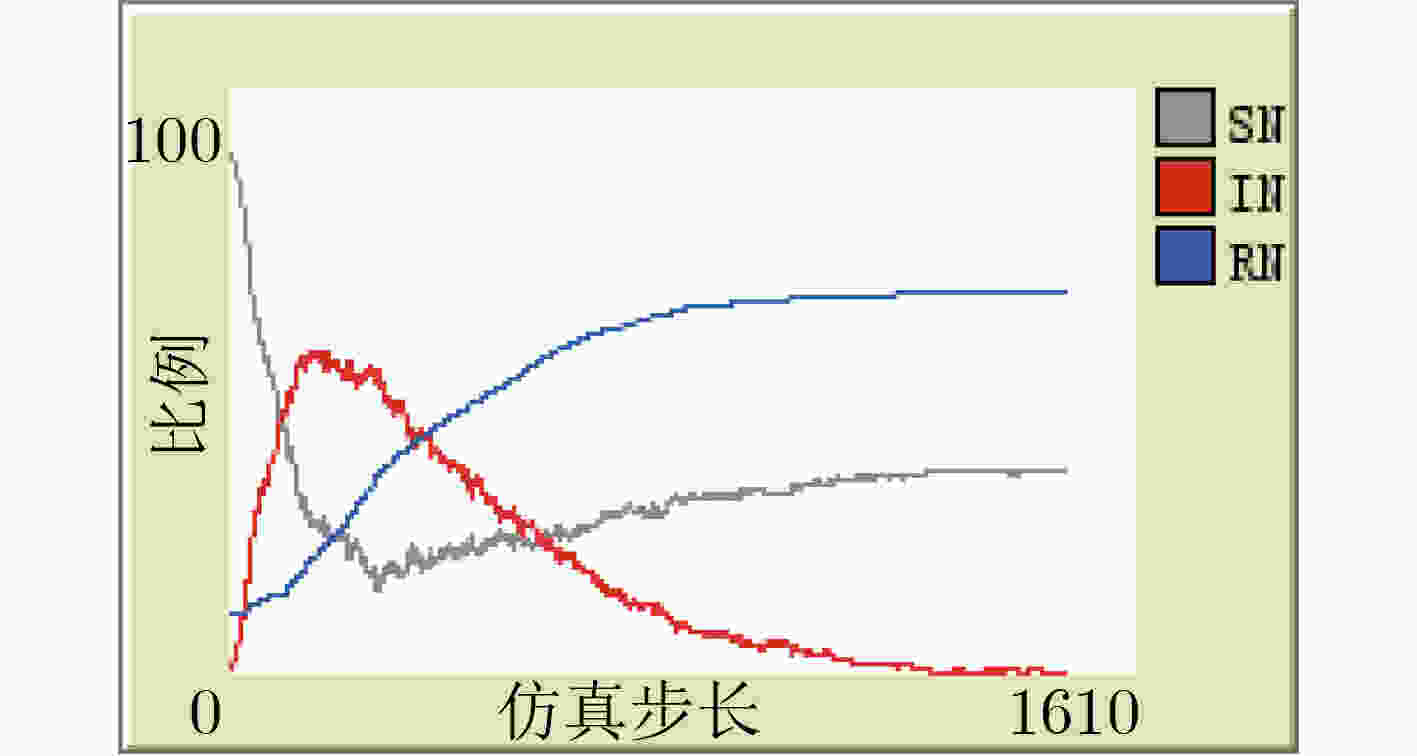
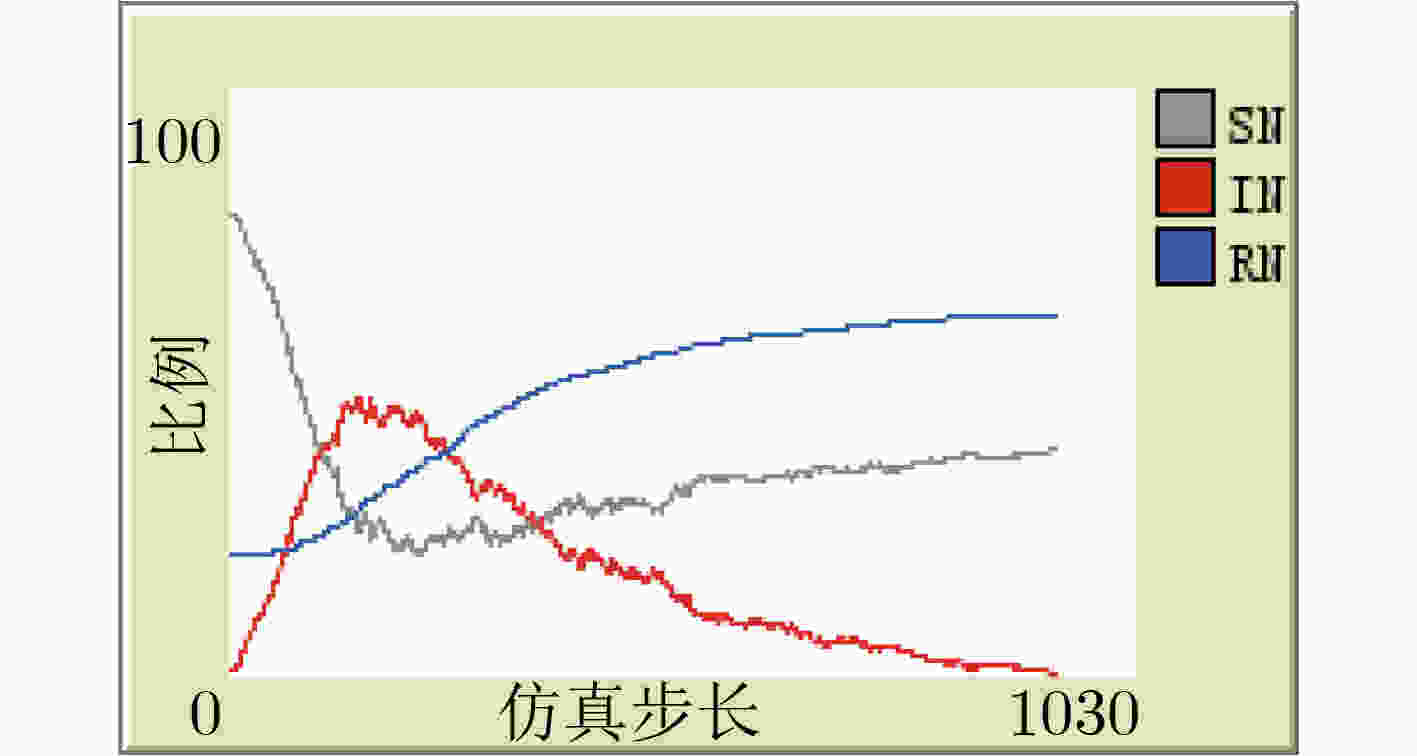
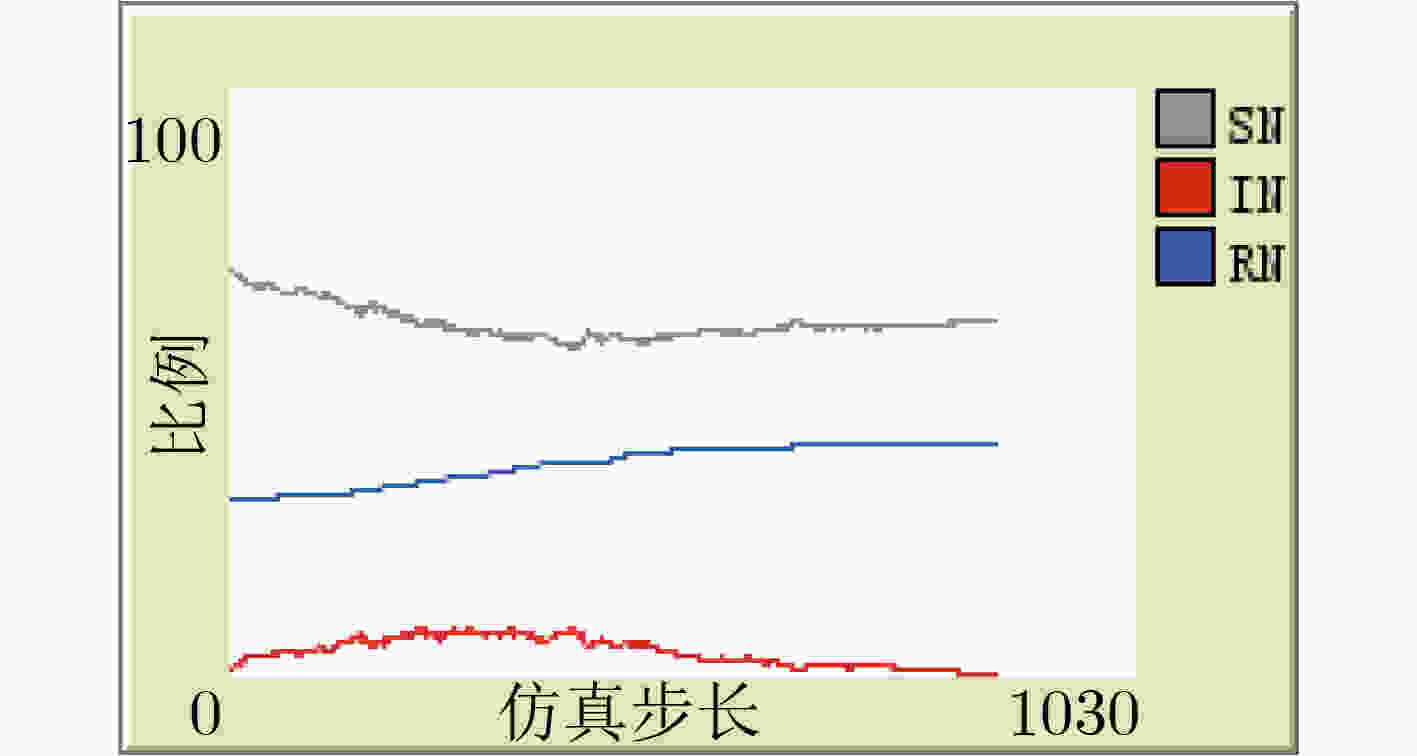
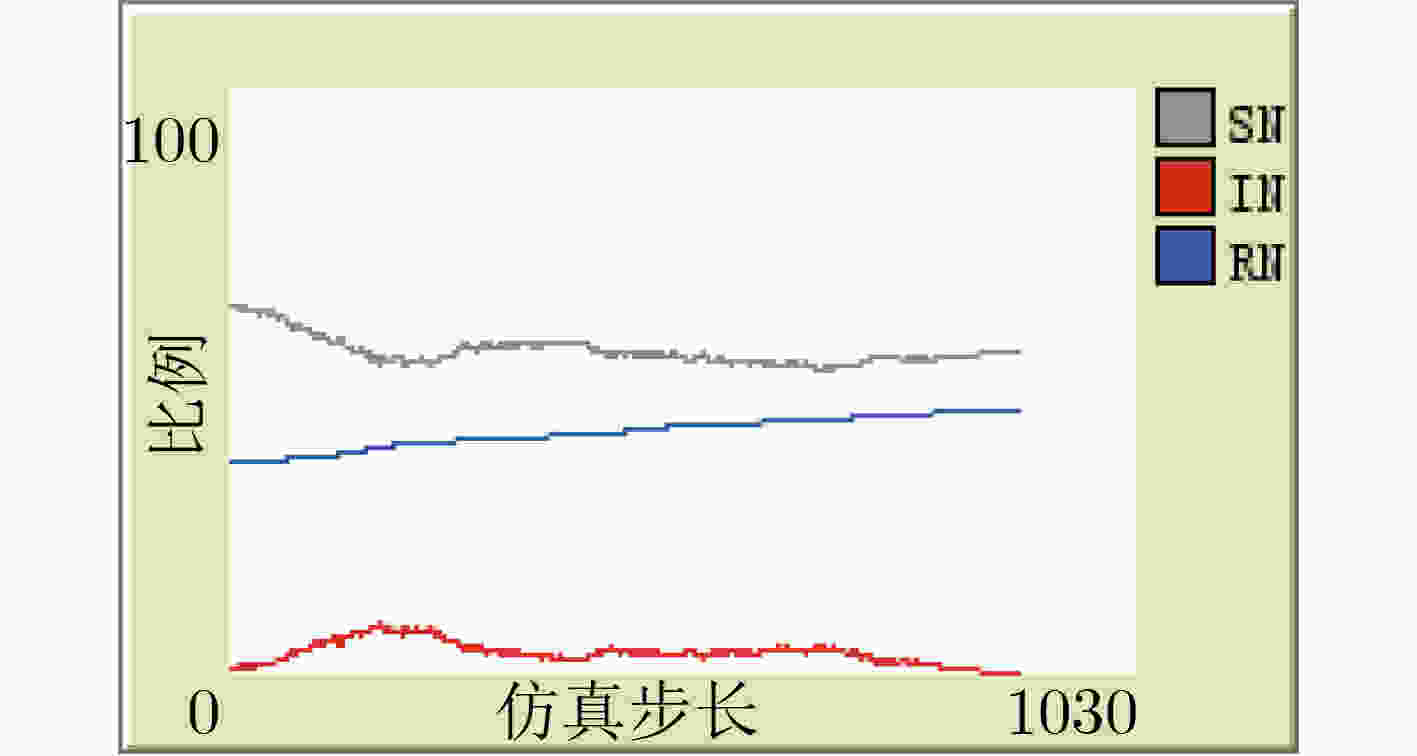
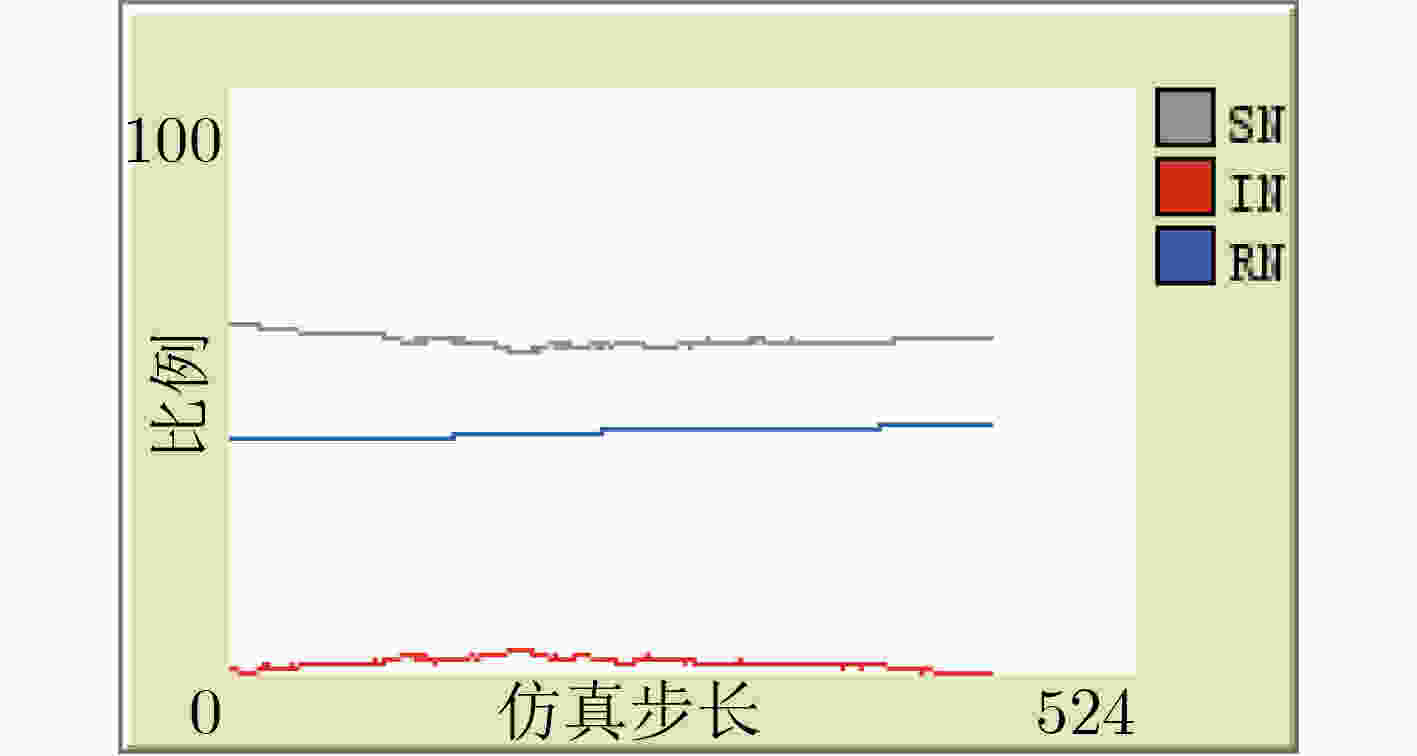
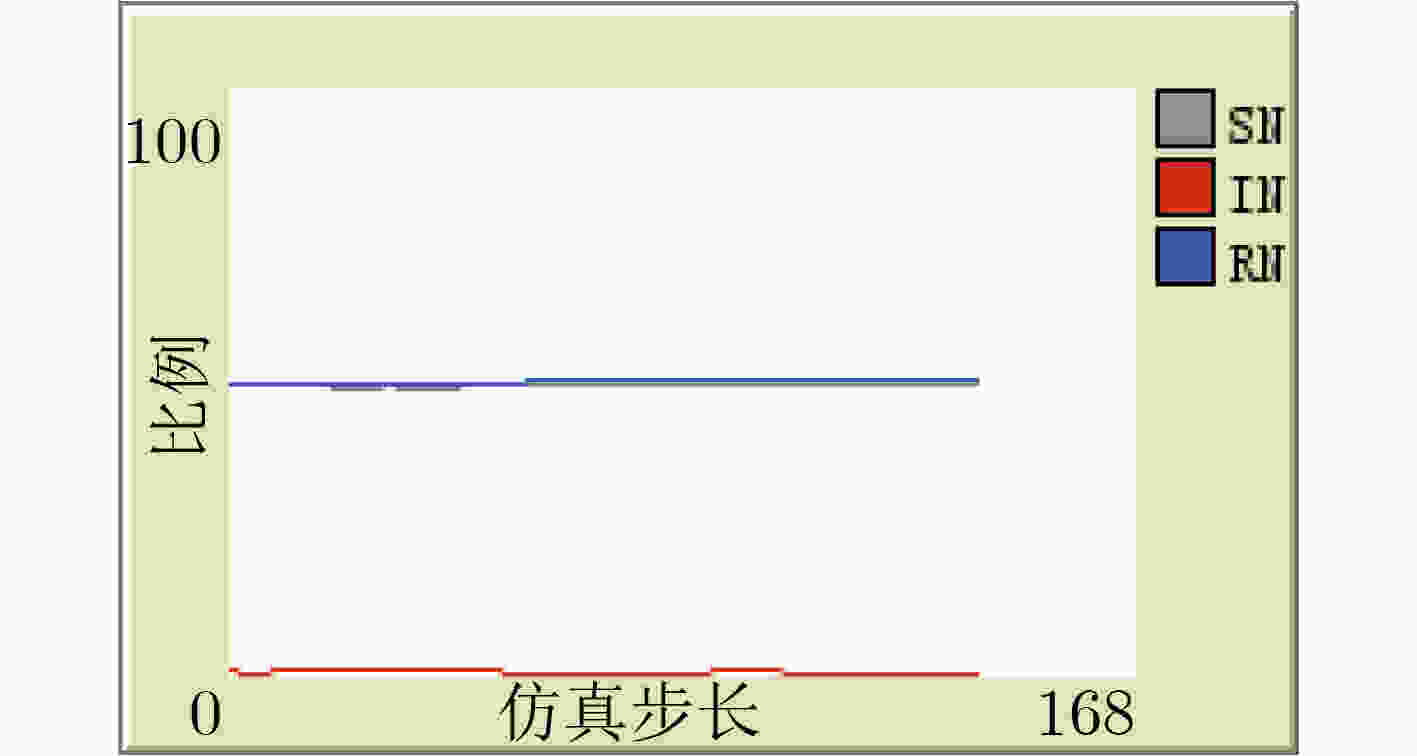


 下载:
下载:
