Howling Removal Based on Analytical Design of All-phase Notch Filter
-
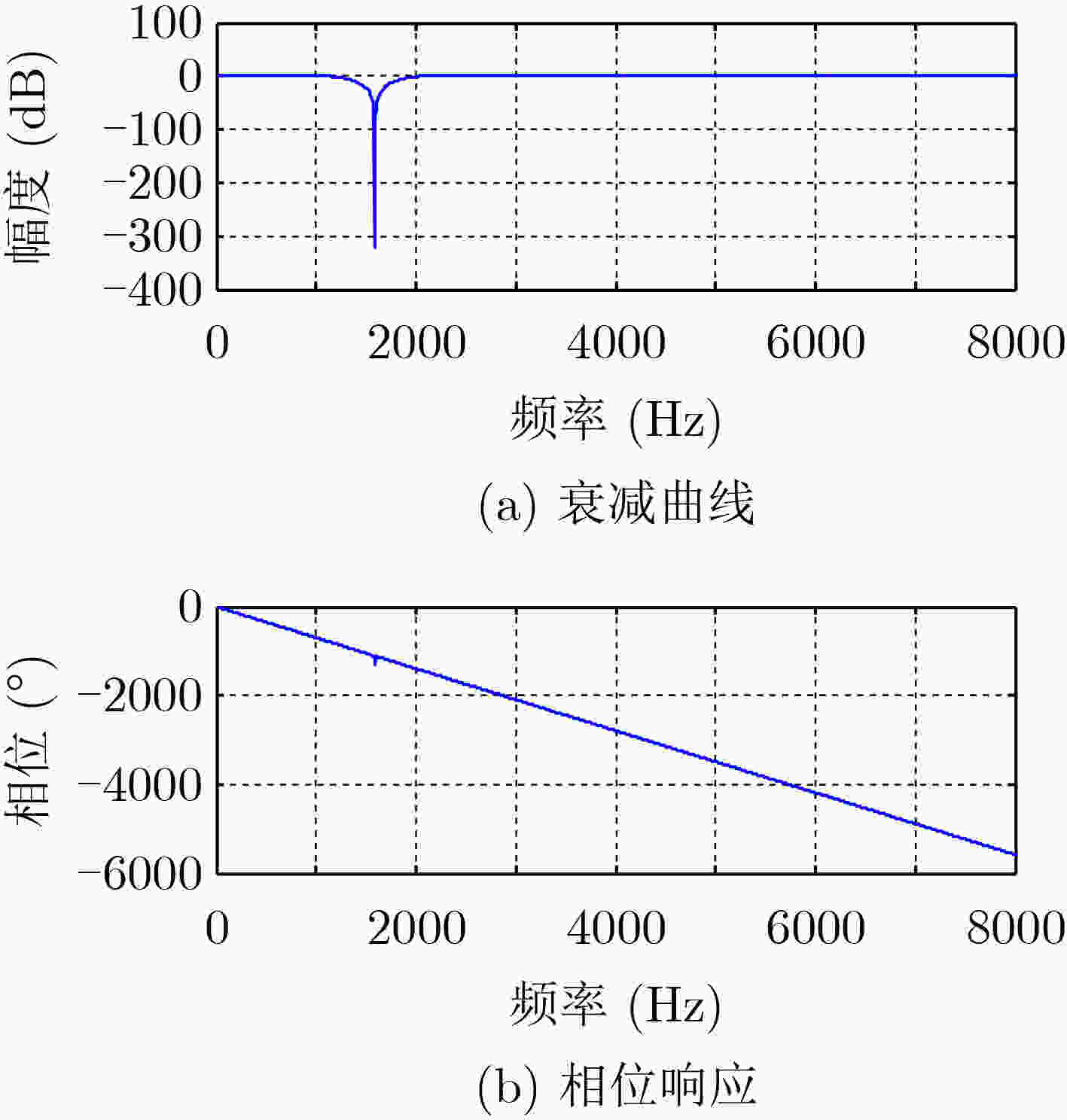
摘要: 为了快速且精准地抑制助听器中的啸叫效应，该文提出一种中心频率可以精确控制的全相位有限脉冲响应(FIR)陷波器解析设计。首先，为了获得较高的陷波精度，引入了整数部分m和小数部分λ来控制陷波的中心频率。然后，设计了一个偶对称的闭式解析式来计算陷波器系数。最后，为了保证输出信号的连续性和线性相位，进行数据延拓和截取操作。该陷波器具有线性传输特性，避免了非线性失真。为了检验陷波器的滤波性能，将其应用在助听器中去除啸叫。实验结果表明，该滤波器在啸叫频率下的衰减值可达–330 dB，信噪比达22 dB，输出波形质量好，算法复杂度低，鲁棒性高，具有一定的应用前景。Abstract: In order to quickly and accurately suppress the howling effect in hearing aids, this paper presents an analytical design of all-phase Finite Impulse Response(FIR) notch filter with explicit controllable center frequency. Firstly, to obtain the higher accuracy, integer m and decimal λ are introduced to control the central frequency of the notch filter. Then, an even symmetric closed-form analytic formula is designed to complete the design of the notch filter, which shows that the proposed notch filter has linear transmission characteristics and avoids nonlinear distortion. Finally, data extension and interception are carried out to ensure the continuity and linear phase of the output signal. Herein, the proposed notch filter is inserted into hearing aid to suppress the howling for the sake of verifying its performances. The experimental results show that the attenuation value of the proposed filter at the howling frequency can reach –330 dB, and the SNR is 22 dB. Moreover, the proposed filter is of good output waveform quality, low algorithm complexity and high robustness, and it has a certain application prospect.
-
1. 引言
随着雷达的广泛应用和信息技术的迅速发展，干扰已成为雷达对抗技术的重要方面。目前，投放和布设具有特定散射特性的无源目标，是实现无源形式雷达干扰的关键手段，由于目标的雷达散射特性对隐真示假干扰效果具有决定性影响，因此雷达目标散射特性的调控技术受到了越来越多的研究关注。在雷达散射截面调控领域，可通过目标的雷达散射截面增强设计以实现对回波信号幅度的增强，这在多种应用场景中发挥着重要作用[1]。例如，为了提高战场中己方真实平台执行任务的成功率，可采用经特定散射截面增强设计的雷达诱饵干扰敌方雷达的探测与跟踪，以达到吸引火力的目的。在救生艇、舢板等小型平台中，雷达散射截面增强设计可帮助提升海事搜救效率以及航行安全；在汽车自动驾驶应用场景中，雷达散射截面增强设计可用于增加道旁弱散射物体的可探测性以协助行车安全。对于无人机、诱饵弹等小型目标平台，平板状金属体通常是其主体结构的重要组成部件之一，也是电磁散射研究中的经典散射体之一。当平面电磁波正入射于平板状金属体的主平面时，由于镜面反射效应，平板状金属体可产生较大的后向散射截面[2]。然而，平板状金属体的厚度一般远小于侧向尺寸，在平面电磁波侧向入射时，后向散射截面急剧减小。考虑到实际的应用场景中，当照射雷达与目标相距较远时，目标处的照射波即可近似为侧向入射情形，因此针对平面电磁波侧向入射时的平板状金属体开展后向散射截面增强设计具有实际意义。
传统的后向散射截面增强技术与设备主要包括角反射器[3]、龙勃透镜[4,5]、方向回溯阵[6]等。通过多次反射、同相回射原理，二面角反射器、三面角反射器以及龙勃透镜可在一定角域和一定频域内提供稳定的后向散射截面增强，但其电大尺寸导致这类设备通常具有体积大、重量大或者制作成本高等缺点，难以共形安装于主体外形需要优先满足空气动力学要求的空基平台表面。通过相位梯度翻转思想，采用贴片天线单元的方向回溯阵具有低剖面和易集成的优点，但其产生定向回波的角域范围与天线单元的主瓣宽度及阵元间距密切相关，难以针对侧向入射形成稳定的回波强度。作为超材料的2维形式，超表面具有低剖面和易于物理实现的优点，近年来在光学、微波以及声学领域出现了许多超表面相关的研究和应用热点。由于超表面在电磁波操控方面表现出的灵活性，在雷达散射截面调控领域中也得到了较多报道，包括雷达散射截面减缩[7-9]、雷达散射截面增强[10,11]、雷达散射截面动态调控[12,13]。但是，文献报道的这些超表面设计主要针对平面电磁波正入射或斜入射情形，对侧向入射情形的雷达散射截面调控设计鲜有涉及。针对平面电磁波侧向照射，文献[14]通过适当设计两支电单极子(Electric Monopole, EM)导体柱的尺寸与间距，在两支电单极子导体柱表面形成了幅度接近相等而相位完全相反的表面感应电流分布，从而提出了准超方向性再辐射概念，并将相应结构加载于薄导电板表面，为薄导电板的侧向回射提供了可观的增强幅度。因为所提出的设计在原理上依赖于半波长电偶极子(Electric Dipole, ED)谐振，所以用于加载的导体柱剖面高度为0.24λ0 (λ0为设计频率对应的自由空间波长)。另一方面，介质谐振器因其损耗小、几何结构紧凑和易于集成等优点而在光学和微波器件中得到了广泛应用。基于介质谐振器单元或阵列，已报道的应用包含了滤波器[15]、功率分配器[16]、介质谐振器天线[17]、超材料[18]和超表面[19]等。通过调节电谐振和磁谐振模式，具备抑制后向散射和增强前向散射能力的介质谐振器或纳米粒子已被用于纳米天线[20-23]。同时，包括龙勃透镜在内，介质体折射率所引起的透射射线偏转特性也被用于设计光子纳米射流，实现对入射平面电磁波的透射聚焦[24,25]，适用于雷达散射截面增强的介质谐振器设计则鲜有报道。
为了在低剖面条件下实现薄导电板在平面电磁波侧向入射时的后向散射截面增强，本文通过介质谐振器设计，研究了基于磁偶极子的超方向性再辐射。通过设计长方介质体的几何尺寸，结合平面电磁波激励，在腔内诱导形成合适的混合谐振(Hybrid ElectroMagnetic, HEM)模式，谐振频率处的腔内场分布和远区再辐射场特征表明介质谐振器起着磁偶极子(Magnetic Dipole, MD)的作用。在此基础上，将两个相同的介质谐振器沿着入射波传播方向紧密级联以组成一个超单元，观察到紧密相邻的这两个介质谐振器内部的磁场强度(H)和电场强度(E)矢量均呈现反向分布而幅度相当，由此产生准超方向性再辐射。此外，考虑到薄导电板尺寸的变化，研究了超单元的不同布阵方式对后向散射截面增强效果的影响。结果表明，所设计的介质谐振器超单元及其阵列对薄导电板的侧向回射具有显著的增强作用，且介质谐振器的剖面厚度仅为0.078λ0。通过双站和单站散射方向图，探究了设计频率处相应散射截面维持增强效果的角域范围。
2. 介质谐振器的谐振与散射特征
2.1 长方介质体的磁偶极子谐振
如图1所示，一个处于自由空间并受到沿+x到–x方向传播的θ极化平面电磁波照射的长方介质体，其沿x, y和z轴的几何尺寸分别表示为a, b和2h。长方介质体的相对介电常数与相对磁导率分别为εr=25和μr=1，并假设其没有损耗。
通过高频电磁结构模拟器Ansys HFSS对图1所示模型进行全波仿真，对于长方介质体几何尺寸a=4.3 mm(0.13λ0，λ0≈33.3 mm是设计频率9 GHz对应的自由空间波长)，b=16 mm(0.48λ0)，h=2.61 mm(0.078λ0)，得到共极化后向散射截面的频率响应曲线如图2(a)所示，在设计频率9 GHz附近观察到一个明显的后向散射截面峰值，其值为–29.84 dBsm。根据图2(b)和图2(c)所示9 GHz处的2维双站散射方向图，观察到长方介质体在xz面内的再辐射方向图接近于全向，而在yz面和xy面内的再辐射方向图则有两个明显的零点位于y轴方向，对应的3维形式双站散射方向图类似于甜甜圈形状；同时，由于xz面内θ分量、yz面内φ分量、xy面内θ分量占主导，结合雷达散射截面的基本定义，可知散射电场强度主分量平行于xz面，散射磁场强度主分量平行于yz面和xy面，相应的正交极化分量(xz面内φ分量、yz面内θ分量、xy面内φ分量，xz面内φ分量与xy面内φ分量均小于–90 dBsm)幅度小至可忽略不计。根据双站散射方向图特征，可知由θ极化平面电磁波激励的这一长方介质体在9 GHz可以等效视为一个沿y轴放置的磁偶极子进行再辐射。
为了加深对这种再辐射的理解，已在图1中绘制了9 GHz处的磁场强度与电场强度分布。长方介质体内出现的驻波场分布是由内部场在介质体和空气各交界面间的多次反射引起的，这意味着该介质体此时形成了介质谐振器。由于磁场强度与电场强度均包含沿x, y和z轴的非零分量，所获得的驻波场分布对应于HEM模式。根据电场强度沿3个坐标轴的半波变化，可知该谐振模式为HEM111模，而HEM111模对应着磁偶极子谐振特性，这与前述的双站散射方向图观察结论一致。因为该介质谐振器可等效视为一个沿y轴放置的磁偶极子，当θ极化平面电磁波的入射角度在xz平面内变化时，也能在9 GHz处观察到类似的散射特征。此外，通过合适地设计，其它几何形状与相对介电常数也可用于实现这种磁偶极子谐振特性。
2.2 基于磁偶极子的超单元及其后向散射截面
以产生磁偶极子谐振的长方介质谐振器作为基本单元，通过级联方式构建了可以增强散射强度的超单元，其结构如图3(a)所示。具体地，相对于初始的基本单元，将第2个基本单元沿入射平面波的传播方向位移一段距离，使得两个基本单元之间的空气间隙为s=1 mm(0.03λ0)。作为比较，文献[14]中涉及的由两个半波长电偶极子组成的超单元示于图3(b)，两支导体柱几何尺寸如下：r1=0.4 mm(0.012λ0), h1=6.8 mm(0.2λ0), s1=4.4 mm(0.13λ0), r2=0.8 mm(0.024λ0), h2=7.9 mm(0.24λ0)。
在沿+x到–x方向传播的θ极化平面电磁波照射下，这两种超单元的后向散射截面频率响应曲线对比结果如图4(a)所示。基于磁偶极子和电偶极子的超单元的后向散射截面峰值均位于9 GHz处，其值分别等于–22.68 dBsm和–22.75 dBsm。可以发现，基于磁偶极子的超单元在谐振频率处产生的后向散射截面与基于电偶极子的超单元相当。相对于图1所示的初始基本单元，基于磁偶极子的超单元产生了7.16 dB的后向散射截面增强。为了进一步理解基于磁偶极子的超单元所产生的后向散射截面峰值，在图4(b)中绘制了9 GHz处的磁场强度与电场强度矢量。观察到存在于第1个基本单元和第2个基本单元内的磁场与电场均表现出反相的状态，幅度则相互接近。由于两个基本单元之间的间距远远小于波长，这种类型的场分布使得基于磁偶极子的超单元类似于一个基于磁偶极子的二元准超方向性阵列。因此，由所设计的超单元产生的准超方向性再辐射有益于增强后向散射截面。此外，通过增加介质谐振器基本单元沿x轴的尺寸，在基本单元中形成的HEM211模式也可用于在9 GHz实现相似的反相场分布和后向散射截面。
3. 薄导电板的侧向回射增强
根据图4(b)，两个介质谐振器基本单元内部及邻近空间中的磁场强度矢量平行于xy面，而在z=0 mm平面则有电场强度矢量垂直于xy面。若将超单元中两个介质谐振器基本单元沿z轴的剖面厚度减半，并加载于薄导电板表面，由于薄导电板表面近似于理想电导体特性，根据电磁场边界条件以及镜像原理，在保持入射波条件不变的前提下，剖面厚度减半且加载于薄导电板表面之后的超单元内部及邻近空间仍可维持与图4(b)中z≥0 mm或z≤0 mm空间几乎相同的磁场强度和电场强度分布，与之伴随的准超方向性再辐射故而可用于增强薄导电板在平面电磁波侧向照射时的后向散射截面。
如图5(a)所示，对于一块侧向尺寸为la×lb=66 mm×66 mm(2λ0)、厚度为t=2 mm(0.06λ0)的薄导电板，在其上表面和下表面均加载一个超单元，且超单元中第1个基本单元沿x轴的中心点与薄导电板前缘之间的距离为sm=8.25 mm(0.25λ0)。为了比较，将图3(b)所示基于电偶极子的超单元剖面高度减半，得到基于电单极子的二元准超方向性再辐射阵列，并将其加载于薄导电板上下表面，超单元中第1支单极子沿x轴的中心点与薄导电板前缘相距se=33 mm(1λ0)，如图5(b)所示。相比于图3，除超单元中介质谐振器或电偶极子沿z轴的剖面高度减半之外，其它尺寸参数保持不变。
图6所示是9 GHz处薄导电板上表面的超单元内部及邻近空间场分布。可以观察到当介质谐振器基本单元沿z轴的剖面高度减半并贴附于导电表面之后，与图4(b)中z≥0 mm空间相似的磁场强度和电场强度分布特性得以维持。由于剖面高度减半，此时电场强度的半波分布变为HEM11δ模式。同时，贴附于导电表面的这两个基本单元内部的磁场强度与电场强度矢量仍呈现相反的旋向而幅度相当。该场分布特性所确立的准超方向性再辐射，使得上下表面加载了磁偶极子超单元的薄导电板在9 GHz处形成了一个值为–21.5 dBsm的后向散射截面峰值，如图7(a)所示，这与加载了电单极子超单元的薄导电板所对应的–23 dBsm峰值接近；相对于未加载超单元的薄导电板，磁偶极子超单元加载措施在谐振频率处获得了31.1 dB的后向散射截面增强，后向散射截面增幅在10 dB以上的频率范围为8.3～9.28 GHz(11.15%)，薄导电板的侧向回射能力由此得以提升。此外，图7(b)给出了9 GHz时加载了超单元和未加载超单元的薄导电板在入射侧xz面和xy面内的双站散射截面，对源于+x轴的侧向入射，两种超单元加载措施均围绕入射波方向形成了一个明显的主散射波瓣，薄导电板在侧向入射情形下的散射特性进而得以修改，磁偶极子超单元加载措施在xz面内双站散射截面增幅大于10 dB的角域范围为128°(θ=90°±64°)，对于xy面所示角度则均超过10 dB。图7(c)给出了入射波频率为9 GHz而入射波角度在xz面和xy面内变化时的后向散射截面，在设计角度+x轴附近，磁偶极子超单元加载措施xz面和xy面内后向散射截面增幅大于10 dB的角域范围分别为30°(θ=90°±15°)和104°(φ=0°±52°)。
当薄导电板的侧向尺寸增大时，可采用超单元组阵的方式以增加介质谐振器对侧向回射的贡献。对于侧向尺寸为la×lb=264 mm×66 mm(8λ0×2λ0)、厚度为t=2 mm(0.06λ0)的薄导电板，在其上下表面加载沿x轴等距排布的磁偶极子超单元，相邻超单元之间的间距为dx=33.7 mm(1.01λ0)，其结构如图8所示。其中，前缘间距sm=8.25 mm(0.25λ0)与前述一致。在平面波侧向照射下，加载了由磁偶极子超单元组成的x向1维线阵的薄导电板的后向散射截面如图9(a)所示。由于超单元之间的互相耦合，后向散射截面峰值发生了一定的频率偏移，位于8.82 GHz，其值为–4.63 dBsm；相比于薄导电板未加载情形，8.82 GHz处的后向散射截面增强了32.32 dB，增幅在10 dB以上的频率范围覆盖8.32～9.2 GHz(10.05%)。图9(b)所示是平面波侧向照射时9 GHz处的双站散射方向图，可以看出超单元沿x轴排布形成的1维线阵可进一步增强沿阵列轴向的定向散射能力，在xz和xy面内，侧向来波方向上的主散射波瓣宽度相对于图7(b)均得到了压缩，对于xz面，10 dB以上双站散射截面增幅覆盖角域为82°(θ=90°±41°)；对于xy面，除个别角度外，双站散射截面增幅在所示的绝大多数角度均为10 dB以上。当入射波频率为9 GHz而入射波角度在xz面和xy面内变化时，相应的后向散射截面如图9(c)所示，xz面和xy面内后向散射截面增幅连续大于10 dB的角域范围分别为36°(θ=90°±18°)和128°(φ=0°±64°)，在侧向入射方向附近形成了稳定的后向散射回波强度。
当薄导电板沿y轴的侧向尺寸增加时，图10所示是la×lb=66 mm×264 mm(2λ0×8λ0)、厚度为t=2 mm(0.06λ0)的薄导电板，将超单元沿y轴以间距dy=25 mm(0.75λ0)贴附在其上下表面。在平面波侧向入射时，随频率变化的后向散射截面如图11(a)所示，加载了磁偶极子超单元阵列的薄导电板在8.98 GHz产生了一个后向散射截面峰值，其值为–3.64 dBsm，相对于未加载的薄导电板，后向散射截面增强了37.62 dB，增幅在10 dB以上的频率范围覆盖了8.06～9.6 GHz(17.44%)。根据图11(b)所示9 GHz处的双站散射方向图，由于介质谐振器基本单元内部的磁场强度主分量沿y轴，由超单元组成的y向1维线阵使得xy面内的主散射波瓣明显窄于xz面，xz面内10 dB以上双站散射截面增幅覆盖角域为136°(θ=90°±68°)，对于所示xy面的绝大多数角度，双站散射截面增幅仍为10 dB以上。同时，根据图11(c)所示9 GHz处的单站散射方向图，xz面和xy面内后向散射截面增幅大于10 dB的角域范围分别为40°(θ=90°±20°)和126°(φ=0°±63°)。
为了验证上述基于全波仿真结果的分析，进行了样件加工及后向散射截面测量，样件照片如图12所示。侧向尺寸为la×lb=66 mm×82.5 mm(2λ0×2.5λ0) 、厚度为t=2 mm(0.06λ0)的薄导电板由铝制成，其上下表面的相同位置处贴附了3个沿y轴排布的超单元，构成超单元的介质谐振器基本单元由标称值εr=25、tanδe≈0.01的三氧化二铝陶瓷制成。此外，在铝板上下表面贴附了相对介电常数约为1.06的聚甲基丙烯酰亚胺泡沫，结合塑料螺钉，用以固定超单元及介质谐振器基本单元的位置。
后向散射截面测量实验在微波暗室中完成，由一对相同且与矢量网络分析仪相连的宽带喇叭天线完成发射和接收，样件和校准铝板位于喇叭天线远场区，在沿+x到–x方向传播的θ极化平面电磁波照射下，通过相对标定法恢复出待测物的后向散射截面。图13对比了相应的全波仿真结果和实验测量结果。对于加载有磁偶极子超单元的铝板样件，仿真所得9 GHz处后向散射截面峰值为–13.5 dBsm，其后向散射截面测量结果相对于仿真结果产生了一定的频率偏移，测得的后向散射截面峰值位于9.24 GHz，其值为–14.79 dBsm，产生频偏的主要原因是所加工制作的微波陶瓷实际的相对介电常数相对于标称值具有一定程度的负公差。除频偏之外，观察到样件测得的后向散射截面峰值相比于仿真结果出现了一定的幅度差异，这主要是由于样件采用的微波陶瓷具有介电损耗，而全波仿真模型采用了无耗的长方介质体以便于分析和讨论工作原理及最优结果。同时，微波陶瓷与定位泡沫的几何尺寸加工误差会影响超单元中两个基本单元之间的间距s，以及定位泡沫的安装误差可能对前缘间距sm产生影响。此外，在实验过程中，由所搭建的测试平台造成的喇叭天线波束指向角与待测物之间的角度对准等因素也会对实验结果带来一定的误差。相对于铝板未加载情形，后向散射截面增幅超过10 dB的频率范围仿真结果为8～9.54 GHz(17.56%)、测量结果为8.25～9.48 GHz(13.87%)。总体而言，对于加载有磁偶极子超单元的铝板以及未加载的铝板，随频率变化的后向散射截面测量结果与仿真结果基本吻合，验证了此设计的有效性。
4. 结论
本文基于介质谐振器的磁偶极子谐振构造了准超方向性再辐射二元阵，并将其作为超单元以增强薄导电板在平面电磁波侧向照射下的后向散射截面。探究了超单元的不同组阵形式对薄导电板侧向回射特性的增强程度。相比于已报道的电单极子超单元，基于磁偶极子的超单元在谐振频率处产生后向散射截面峰值的同时，其剖面高度仅为0.078λ0，剖面高度缩减66.96%，有助于低剖面集成。综上，本文提出的设计具备修改薄导电板侧向回射特性的能力以及低剖面的特点，对小型目标平台中的类平板状部件的后向散射截面增强设计具有一定的参考意义，进而为雷达诱饵、海事救援以及智能交通等应用场景提供支撑。
-
表 1 啸叫频率f0与SNR(N=32)
f0(Hz) SNR(dB) f0(Hz) SNR(dB) 1290 21.2816 2490 22.1826 1590 21.9162 2790 22.1217 1890 21.9733 3090 22.0438 2190 22.1121 3390 22.0071 
下载: 导出CSV
表 2 陷波器阶数N与SNR(f0=1590 Hz)
阶数N SNR(dB) 阶数N SNR(dB) 32 21.9162 256 22.4311 64 21.8347 512 22.8120 128 21.7462 1024 20.9697
下载: 导出CSV
-
[1] JINDAPETCH N, CHEWAE S, and PHUKPATTARANONT P. FPGA implementations of an ADALINE adaptive filter for power-line noise cancellation in surface electromyography signals[J]. Measurement, 2012, 45(3): 405–414. doi: 10.1016/j.measurement.2011.11.004 [2] MAHMOODI S N, CRAFT M J, SOUTHWARD S C, et al. Active vibration control using optimized modified acceleration feedback with adaptive line enhancer for frequency tracking[J]. Journal of Sound and Vibration, 2011, 330(7): 1300–1311. doi: 10.1016/j.jsv.2010.10.013 [3] PASCO Y, ROBIN O, BÉLANGER P, et al. Multi-input multi-output feedforward control of multi-harmonic gearbox vibrations using parallel adaptive notch filters in the principal component space[J]. Journal of Sound and Vibration, 2011, 330(22): 5230–5244. doi: 10.1016/j.jsv.2011.06.008 [4] 肖玮, 涂亚庆, 刘良兵, 等. 频率估计的差频等长信号加权融合算法[J]. 信号处理, 2011, 27(7): 1106–1111. doi: 10.3969/j.issn.1003-0530.2011.07.023XIAO Wei, TU Yaqing, LIU Liangbing, et al. A weight-fusion algorithm for frequency estimation of the signal with the known frequency-difference and the same length[J]. Signal Processing, 2011, 27(7): 1106–1111. doi: 10.3969/j.issn.1003-0530.2011.07.023 [5] FENG Y Q, TANG G C, LIANG R Y, et al. An improved echo cancellation algorithm for hearing aids[C]. The 2015 International Conference on Electronics, Electrical Engineering and Information Science (EEEIS2015), Guangzhou, China, 2016: 362–369. doi: 10.1142/9789814740135_0038. [6] LIANG Ruiyu, WANG Xia, WANG Qingyun, et al. A joint echo cancellation algorithm for quick suppression of howls in hearing aids[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2017, 12(4): 565–574. doi: 10.1002/tee.22412 [7] VAN WATERSCHOOT T and MOONEN M. Fifty years of acoustic feedback control: State of the art and future challenges[J]. Proceedings of the IEEE, 2011, 99(2): 288–327. doi: 10.1109/JPROC.2010.2090998 [8] ZAHRADNIK P and VLCEK M. Fast analytical design algorithms for FIR notch filters[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(3): 608–623. doi: 10.1109/TCSI.2003.822404 [9] LAI Xiaoping. Constrained Chebyshev design of FIR filters[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2004, 51(3): 143–146. doi: 10.1109/TCSII.2003.821523 [10] 孙小君, 周晗, 闫广明. 基于新息的自适应增量Kalman滤波器[J]. 电子与信息学报, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493SUN Xiaojun, ZHOU Han, and YAN Guangming. New information based adaptive incremental Kalman filter[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493 [11] 维纳·K. 恩格尔, 约翰·G. 普罗克斯, 刘树棠, 译. 数字信号处理: 使用MATLAB[M]. 西安: 西安交通大学出版社, 2002: 181–188.INGLE V K and PROAKIS J G, LIU Shutang, translation. Digital Signal Processing[M]. Xi’an: Xi’an Jiaotong University Press, 2002: 181–188. [12] PRIOAKIS J G and MANOLAKIS D G. Digital Signal Processing: Principle, Algorithms, and Application[M]. New Jersey: Prentice Hall, 2006: 112–114. [13] PUNCHALARD R, LORSAWATSIRI A, KOSEEYAPORN J, et al. Adaptive IIR notch filters based on new error criteria[J]. Signal Processing, 2008, 88(3): 685–703. doi: 10.1016/j.sigpro.2007.09.010 [14] 涂亚庆, 苏奋华, 沈廷鳌, 等. 自适应陷波器的科氏流量计信号频率跟踪方法[J]. 重庆大学学报, 2011, 34(10): 147–152.TU Yaqing, SU Fenhua, SHEN Tingao, et al. Frequency tracking method and simulation for Coriolis mass flowmter based on a new adaptive notch filter[J]. Journal of Chongqing University, 2011, 34(10): 147–152. [15] HUANG Xiangdong, JING Senxue, WANG Zhaohua, et al. Closed-form FIR filter design based on convolution window spectrum interpolation[J]. IEEE Transactions on Signal Processing, 2016, 64(5): 1173–1186. doi: 10.1109/TSP.2015.2494869 [16] 黄翔东, 王兆华. 基于两种对称频率采样的全相位FIR滤波器设计[J]. 电子与信息学报, 2007, 29(2): 478–481.HUANG Xiangdong and WANG Zhaohua. All-phase FIR filter design based on two kinds of symmetric frequency sampling[J]. Journal of Electronics &Information Technology, 2007, 29(2): 478–481. [17] CARNEY R. Design of a digital notch filter with tracking requirements[J]. IEEE Transactions on Space Electronics and Telemetry, 1963, 9(4): 109–114. doi: 10.1109/tset.1963.4337624 [18] LEOTWASSANA W, PUNCHALARD R, and SILAPHAN W. Adaptive howling canceller using adaptive IIR notch filter: Simulation and implementation[C]. Proceedings of 2003 International Conference on Neural Networks and Signal Processing, Nanjing, China, 2003: 848–851. doi: 10.1109/ICNNSP.2003.1279409. 期刊类型引用(2)
1. 杨培消，窦高奇，高俊，陈盈. 基于软件无线电平台的DDST传输技术研究. 通信技术. 2018(05): 1021-1025 . 
百度学术2. 杨顺峰，姜斌，包建荣，刘超. 基于叠加训练序列的ACO-OFDM信道估计. 杭州电子科技大学学报(自然科学版). 2017(04): 25-29 . 百度学术其他类型引用(5)
-
下载:
百度学术
计量
- 文章访问数: 1277
- HTML全文浏览量: 574
- PDF下载量: 61
- 被引次数: 7
下载:
