动态加权条件互信息的特征选择算法

张俐; 陈小波

doi:10.11999/JEIT200615

动态加权条件互信息的特征选择算法

doi: 10.11999/JEIT200615

张俐^{1, 2, ,},
陈小波³

1.
江苏理工学院计算机工程学院常州 213001
2.
北京邮电大学可信分布式计算与服务教育部重点实验室北京 100876
3.
中国人民银行常州市中心支行常州 213001

基金项目: 国家科技基础性工作专项(2015FY111700-6)，江苏理工学院博士科研基金(KYY19042)

详细信息

作者简介:
张俐：男，1977年生，博士，副教授，研究方向为特征选择和机器学习

陈小波：女，1980年生，硕士，工程师，研究方向为特征选择和机器学习

通讯作者:
张俐　zhangli_3913@163.com

中图分类号: TN911.7
计量
- 文章访问数: 1386
- HTML全文浏览量: 1067
- PDF下载量: 149
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-23
- 修回日期: 2021-02-05
- 网络出版日期: 2021-03-19
- 刊出日期: 2021-10-18

Feature Selection Algorithm for Dynamically Weighted Conditional Mutual Information

Li ZHANG^{1, 2
, ,},
Xiaobo CHEN³

1.
College of Computer Engineering, Jiangsu University of Technology, Changzhou 213001, China
2.
Key Laboratory of Trustworthy Distributed Computing and Service (Ministry of Education), Beijing University of Posts and Telecommunications, Beijing 100876, China
3.
The People's Bank of China, Changzhou Branch, Changzhou 213001, China

Funds: The National Science and Technology Basic Work Project (2015FY111700-6), The Doctoral Research Fund of Jiangsu University of Technology (KYY19042)

摘要

摘要: 特征选择是机器学习、自然语言处理和数据挖掘等领域中数据预处理阶段必不可少的步骤。在一些基于信息论的特征选择算法中，存在着选择不同参数就是选择不同特征选择算法的问题。如何确定动态的非先验权重并规避预设先验参数就成为一个急需解决的问题。该文提出动态加权的最大相关性和最大独立性(WMRI)的特征选择算法。首先该算法分别计算新分类信息和保留类别信息的平均值。其次，利用标准差动态调整这两种分类信息的参数权重。最后，WMRI与其他5个特征选择算法在3个分类器上，使用10个不同数据集，进行分类准确率指标(fmi)验证。实验结果表明，WMRI方法能够改善特征子集的质量并提高分类精度。
- 特征选择 /
- 分类信息 /
- 平均值 /
- 标准差 /
- 动态加权
Abstract: Feature selection is an essential step in the data preprocessing phase in the fields of machine learning, natural language processing and data mining. In some feature selection algorithms based on information theory, there is a problem that choosing different parameters means choosing different feature selection algorithms. How to determine the dynamic, non-a priori weights and avoid the preset a priori parameters become an urgent problem. A Dynamic Weighted Maximum Relevance and maximum Independence (WMRI) feature selection algorithm is proposed in this paper. Firstly, the algorithm calculates the average value of the new classification information and the retained classification information. Secondly, the standard deviation is used to dynamically adjust the parameter weights of these two types of classification information. At last, WMRI and the other five feature selection algorithms use ten different data sets on three classifiers for the fmi classification metrics validation. The experimental results show that the WMRI method can improve the quality of feature subsets and increase classification accuracy.
- Feature selection /
- Classification information /
- Average value /
- Standard deviation /
- Dynamic weighting

HTML全文

图 1 KNN在高维数据集上的性能比较

下载: 全尺寸图片幻灯片

图 2 C4.5在高维数据集上的性能比较

下载: 全尺寸图片幻灯片

图 3 Random Forest在高维数据集上的性能比较

下载: 全尺寸图片幻灯片

表 1 WMRI算法的伪代码

输入：原始特征集合$F = \left\{ { {f_{\rm{1} } },{f_{\rm{2} } }, \cdots,{f_n} } \right\}$，类标签集合$C$，阈　　　　值$K$
输出：最优特征子集$S$
(1)　初始化：$S = \phi $, $k = 0$
(2)　for k=1 to n
(3)　　计算每个特征与标签的互信息值$I\left( {C;{f_k}} \right)$
(4)　 ${J_{{\rm{WMRI}}} }(k) = \arg \max \left( {I\left( {C;{f_k} } \right)} \right)$
(5)　Set $F \leftarrow F\backslash \{ {f_k}\} $
(6)　Set $S \leftarrow \{ {f_k}\} $
(7)　while $k \le K$
(8)　　for each${f_k} \in F$do
(9)　　分别计算新分类信息项$I\left( {C;{f_k}\|{f_{{\rm{sel}}}}} \right)$与保留类别信息项　　　　　$I\left( {C;{f_{{\rm{sel}}}}\|{f_k}} \right)$的值
(10)　　根据式(4)，计算新分类信息项的平均值${\mu _1}$
(11)　　根据式(5)，计算新分类信息项的标准方差$\alpha $
(12)　　根据式(6)，计算保留类别信息项的平均值${\mu _2}$
(13)　　根据式(7)，计算保留类别信息项的标准方差$\beta $
(14)　　根据式(3)，更新${J_{{\rm{WMRI}}}}\left( {{f_k}} \right)$
(15)　end for
(16)　根据${J_{{\rm{WMRI}}}}\left( {{f_k}} \right)$评估标准，寻找最优的候选特征${f_k}$
(17)　Set $F \leftarrow F\backslash \{ {f_k}\} $
(18)　Set $S \leftarrow \{ {f_k}\} $
(19)　k=k+1
(20) end while

下载: 导出CSV

表 2 数据集描述

序号	数据集名称	特征数	样本数	类别数	数据来源
1	musk2	167	476	2	UCI
2	madelon	500	2600	2	ASU
3	ALLAML	7129	72	2	ASU
4	CNAE-9	857	1080	9	UCI
5	mfeat-kar	65	2000	10	UCI
6	USPS	256	9298	10	ASU
7	semeion	257	1593	10	ASU
8	COIL20	1024	1440	20	ASU
9	wpbc	34	198	22	UCI
10	Isolet	617	1560	26	ASU

下载: 导出CSV

表 3 KNN分类器的平均分类准确率fmi(%)

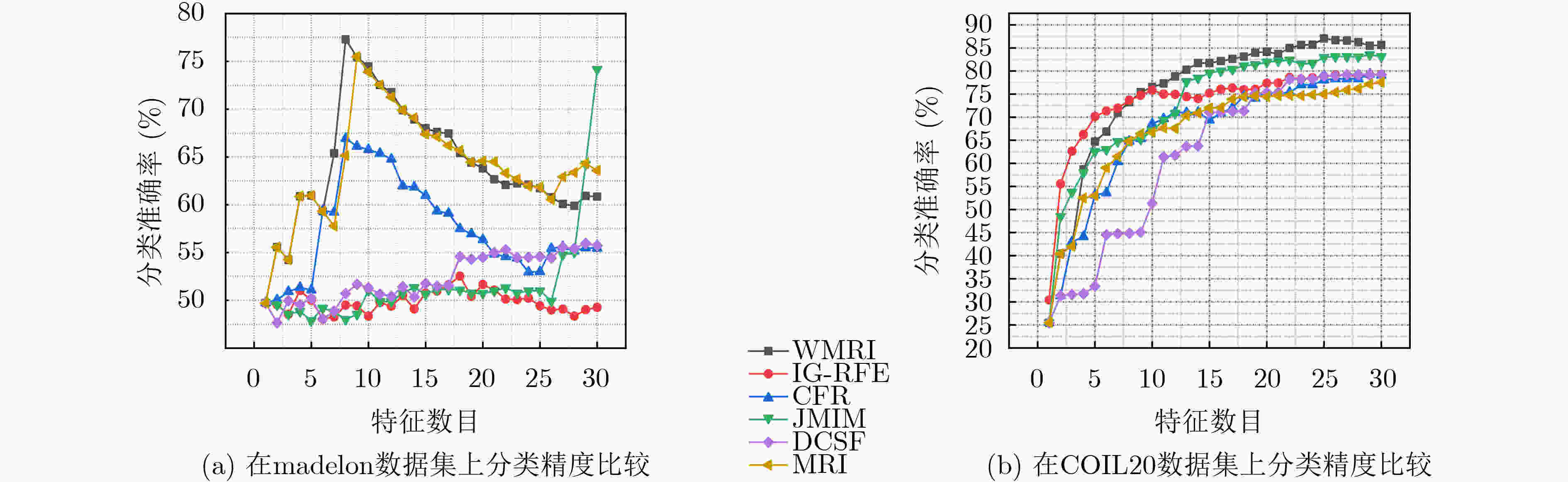
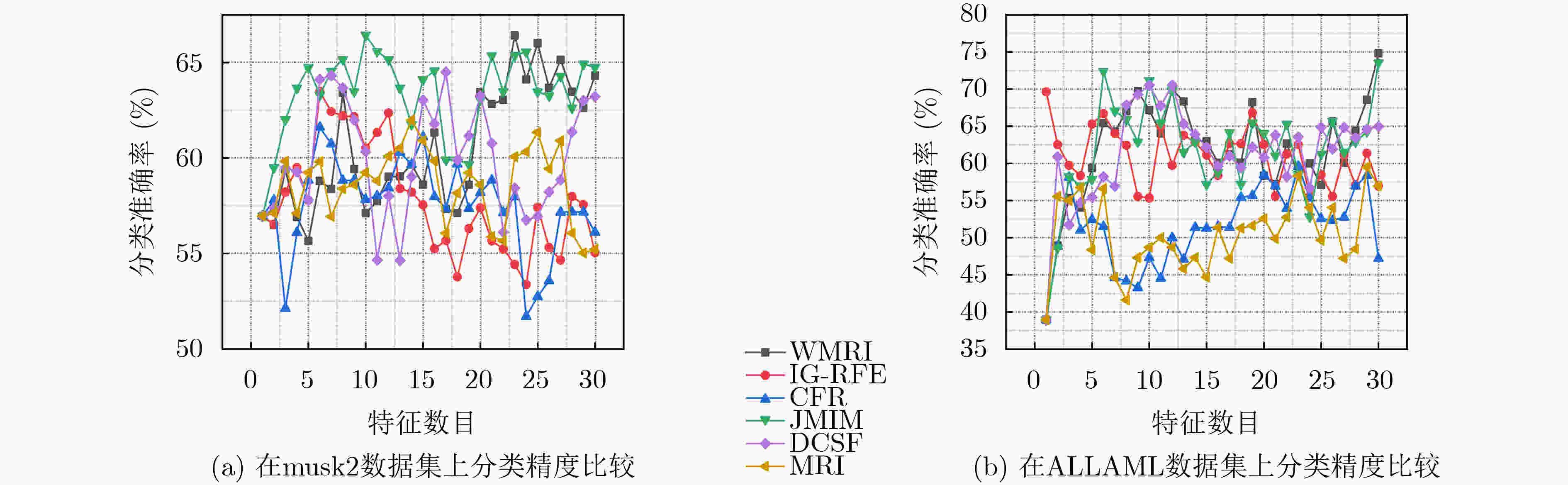
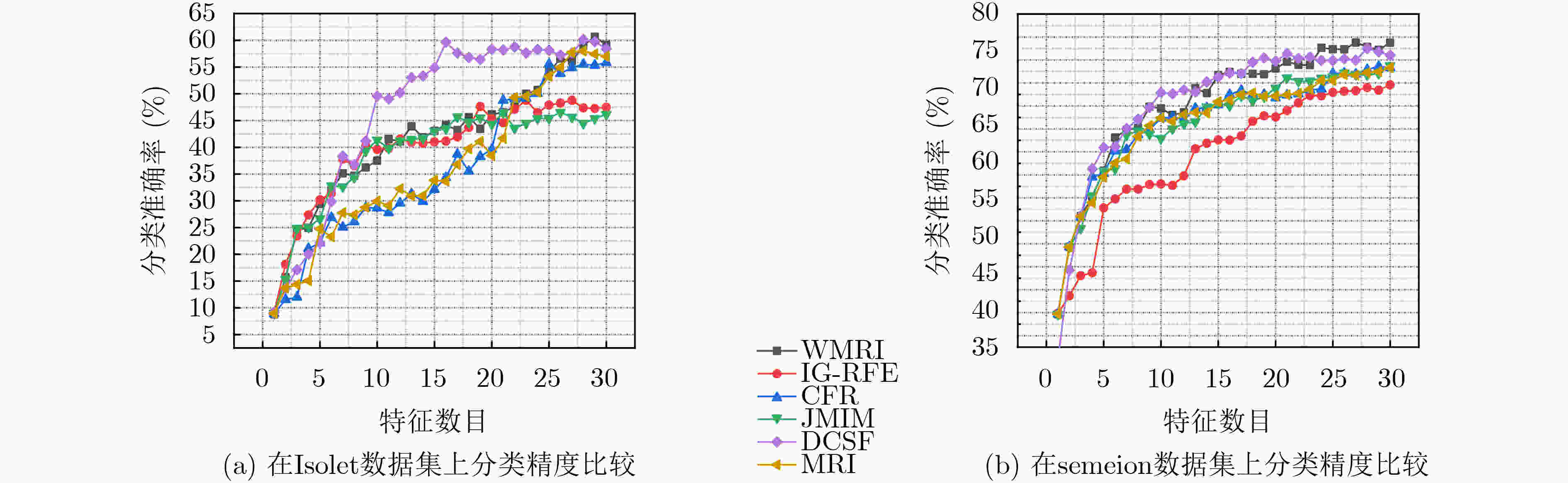
数据集	WMRI	IG-RFE	CFR	JMIM	DCSF	MRI
madelon	79.807	55.037(+)	69.422(+)	76.654(+)	58.465(+)	77.999(+)
USPS	84.372	52.601(+)	55.796(+)	84.372(=)	48.376(+)	62.11(+)
COIL20	87.014	79.236(+)	79.306(+)	83.542(+)	79.236(+)	77.569(+)
musk2	74.002	68.065(+)	70.172(+)	70.592(+)	71.019(+)	69.766(+)
CNAE-9	76.667	74.722(+)	76.667(=)	52.315(+)	76.667(=)	76.667(+)
mfeat-kar	95.961	96.11(–)	95.905(+)	94.459(+)	95.908(+)	95.905(+)
ALLAML	73.873	72.29(+)	68.774(+)	73.873(=)	68.211(+)	62.403(+)
wpbc	36.298	29.482(+)	33.427(+)	27.814(+)	33.423(+)	36.298(=)
Isolet	57.628	47.756(+)	46.795(+)	45.705(+)	51.154(+)	48.91(+)
semeion	75.196	64.981(+)	68.989(+)	55.015(+)	73.501(+)	68.728(+)
平均值	74.082	64.028	66.525	66.434	65.596	67.636
W/T/L		9/0/1	9/1/0	8/2/0	9/1/0	9/1/0

下载: 导出CSV

表 4 C4.5分类器的平均分类准确率fmi(%)

数据集	WMRI	IG-RFE	CFR	JMIM	DCSF	MRI
madelon	79.886	53.653(+)	69.305(+)	65.302(+)	57.808(+)	78.694(+)
USPS	75.94	71.756(+)	76.198(–)	75.66(+)	72.057(+)	77.908(–)
COIL20	78.403	68.889(+)	71.944(+)	72.014(+)	78.333(+)	71.944(+)
musk2	66.42	63.485(+)	61.612(+)	66.433(–)	64.499(+)	61.981(+)
CNAE-9	81.481	80.833(+)	81.481(=)	62.593(+)	81.481(=)	81.481(=)
mfeat-kar	85.058	84.563(+)	84.863(+)	81.612(+)	84.914(+)	84.915(+)
ALLAML	74.815	69.619(+)	59.606(+)	73.553(+)	70.523(+)	59.499(+)
wpbc	35.483	27.942(+)	31.991(+)	29.547(+)	31.757(+)	35.176(+)
Isolet	53.141	41.667(+)	50.513(+)	39.936(+)	52.372(+)	52.244(+)
semeion	72.311	65.974(+)	67.614(+)	55.03(+)	70.435(+)	67.355(+)
平均值	70.258	62.854	65.518	62.183	66.455	67.129
W/T/L		10/0/0	8/1/1	9/0/1	9/1/0	8/1/1

下载: 导出CSV

表 5 Random Forest分类器的平均分类准确率fmi(%)

数据集	WMRI	IG-RFE	CFR	JMIM	DCSF	MRI
madelon	81.308	53.882(+)	70.499(+)	64.306(+)	60.227(+)	81.04(+)
USPS	84.414	79.038(+)	82.791(+)	84.091(+)	79.662(+)	84.018(+)
COIL20	88.681	80.972(+)	82.847(+)	80.278(+)	84.653(+)	82.222(+)
musk2	69.379	65.138(+)	67.886(+)	68.695(+)	67.229(+)	68.917(+)
CNAE-9	82.222	81.667(+)	81.852(+)	62.407(+)	81.944(+)	82.037(+)
mfeat-kar	89.53	83.666(+)	83.812(+)	89.024(+)	87.581(+)	88.52(+)
ALLAML	84.683	72.504(+)	69.367(+)	80.73(+)	71.824(+)	64.132(+)
wpbc	45.655	43.239(+)	45.496(+)	44.105(+)	45.059(+)	44.067(+)
Isolet	60.641	48.782(+)	55.833(+)	46.538(+)	60.128(+)	58.013(+)
semeion	78.722	69.169(+)	73.203(+)	59.113(+)	76.269(+)	73.33(+)
平均值	76.524	67.806	71.359	67.929	71.458	72.63
W/T/L		10/0/0	10/0/0	10/0/0	10/0/0	10/0/0

下载: 导出CSV

参考文献(22)

[1]	CHE Jinxing, YANG Youlong, LI Li, et al. Maximum relevance minimum common redundancy feature selection for nonlinear data[J]. Information Sciences, 2017, 409/410: 68–86. doi: 10.1016/j.ins.2017.05.013
[2]	CHEN Zhijun, WU Chaozhong, ZHANG Yishi, et al. Feature selection with redundancy-complementariness dispersion[J]. Knowledge-Based Systems, 2015, 89: 203–217. doi: 10.1016/j.knosys.2015.07.004
[3]	张天骐, 范聪聪, 葛宛营, 等. 基于ICA和特征提取的MIMO信号调制识别算法[J]. 电子与信息学报, 2020, 42(9): 2208–2215. doi: 10.11999/JEIT190320 ZHANG Tianqi, FAN Congcong, GE Wanying, et al. MIMO signal modulation recognition algorithm based on ICA and feature extraction[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2208–2215. doi: 10.11999/JEIT190320
[4]	ZHANG Yishi, ZHANG Qi, CHEN Zhijun, et al. Feature assessment and ranking for classification with nonlinear sparse representation and approximate dependence analysis[J]. Decision Support Systems, 2019, 122: 113064.1–113064.17. doi: 10.1016/j.dss.2019.05.004
[5]	ZENG Zilin, ZHANG Hongjun, ZHANG Rui, et al. A novel feature selection method considering feature interaction[J]. Pattern Recognition, 2015, 48(8): 2656–2666. doi: 10.1016/j.patcog.2015.02.025
[6]	赵湛, 韩璐, 方震, 等. 基于可穿戴设备的日常压力状态评估研究[J]. 电子与信息学报, 2017, 39(11): 2669–2676. doi: 10.11999/JEIT170120 ZHAO Zhan, HAN Lu, FANG Zhen, et al. Research on daily stress detection based on wearable device[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2669–2676. doi: 10.11999/JEIT170120
[7]	BROWN G, POCOCK A, ZHAO Mingjie, et al. Conditional likelihood maximisation: A unifying framework for information theoretic feature selection[J]. The Journal of Machine Learning Research, 2012, 13(1): 27–66.
[8]	MACEDO F, OLIVEIRA M R, PACHECO A, et al. Theoretical foundations of forward feature selection methods based on mutual information[J]. Neurocomputing, 2019, 325: 67–89. doi: 10.1016/j.neucom.2018.09.077
[9]	GAO Wanfu, HU Liang, ZHANG Ping, et al. Feature selection by integrating two groups of feature evaluation criteria[J]. Expert Systems with Applications, 2018, 110: 11–19. doi: 10.1016/j.eswa.2018.05.029
[10]	肖利军, 郭继昌, 顾翔元. 一种采用冗余性动态权重的特征选择算法[J]. 西安电子科技大学学报, 2019, 46(5): 155–161. doi: 10.19665/j.issn1001-2400.2019.05.022 XIAO Lijun, GUO Jichang, and GU Xiangyuan. Algorithm for selection of features based on dynamic weights using redundancy[J]. Journal of Xidian University, 2019, 46(5): 155–161. doi: 10.19665/j.issn1001-2400.2019.05.022
[11]	WANG Xinzheng, GUO Bing, SHEN Yan, et al. Input feature selection method based on feature set equivalence and mutual information gain maximization[J]. IEEE Access, 2019, 7: 151525–151538. doi: 10.1109/ACCESS.2019.2948095
[12]	GAO Wanfu, HU Liang, and ZHANG Ping. Class-specific mutual information variation for feature selection[J]. Pattern Recognition, 2018, 79: 328–339. doi: 10.1016/j.patcog.2018.02.020
[13]	WANG Jun, WEI Jinmao, YANG Zhenglu, et al. Feature selection by maximizing independent classification information[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(4): 828–841. doi: 10.1109/TKDE.2017.2650906
[14]	GAO Wanfu, HU Liang, ZHANG Ping, et al. Feature selection considering the composition of feature relevancy[J]. Pattern Recognition Letters, 2018, 112: 70–74. doi: 10.1016/j.patrec.2018.06.005
[15]	LIN Xiaohui, LI Chao, REN Weijie, et al. A new feature selection method based on symmetrical uncertainty and interaction gain[J]. Computational Biology and Chemistry, 2019, 83: 107149. doi: 10.1016/j.compbiolchem.2019.107149
[16]	BENNASAR M, HICKS Y, and SETCHI R. Feature selection using joint mutual information maximisation[J]. Expert Systems with Applications, 2015, 42(22): 8520–8532. doi: 10.1016/j.eswa.2015.07.007
[17]	LYU Hongqiang, WAN Mingxi, HAN Jiuqiang, et al. A filter feature selection method based on the maximal information coefficient and Gram-Schmidt orthogonalization for biomedical data mining[J]. Computers in Biology and Medicine, 2017, 89: 264–274. doi: 10.1016/j.compbiomed.2017.08.021
[18]	SHARMIN S, SHOYAIB M, ALI A A, et al. Simultaneous feature selection and discretization based on mutual information[J]. Pattern Recognition, 2019, 91: 162–174. doi: 10.1016/j.patcog.2019.02.016
[19]	SUN Guanglu, LI Jiabin, DAI Jian, et al. Feature selection for IoT based on maximal information coefficient[J]. Future Generation Computer Systems, 2018, 89: 606–616. doi: 10.1016/j.future.2018.05.060
[20]	PENG Hanchuan, LONG Fuhui, and DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226–1238. doi: 10.1109/TPAMI.2005.159
[21]	MEYER P E, SCHRETTER C, and BONTEMPI G. Information-theoretic feature selection in microarray data using variable complementarity[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(3): 261–274. doi: 10.1109/JSTSP.2008.923858
[22]	SPEISER J L, MILLER M E, TOOZE J, et al. A comparison of random forest variable selection methods for classification prediction modeling[J]. Expert Systems with Applications, 2019, 134: 93–101. doi: 10.1016/j.eswa.2019.05.028