A New One-layer Recurrent Neural Network for Solving Nonsmooth Pseudoconvex Optimization Problems
-
摘要: 非光滑伪凸优化问题是一类比较特殊的非凸优化问题,常出现在各类科学与工程应用中,因此具有很大的研究价值。针对现有神经网络模型解决非光滑伪凸优化问题存在的不足,该文基于微分包含理论,提出一种新型单层递归神经网络模型。通过理论分析,证明了神经网络状态解在有限时间内收敛到可行域,且永驻其中,最终神经网络状态解收敛于原优化问题的最优解。最后,通过数值实验,验证了所提理论的有效性。与现有的神经网络相比,该文所提神经网络模型结构简单仅为单层,不需要提前计算罚参数,且对初始点选取没有任何特殊的要求。Abstract: Pseudoconvex optimization problems are a special kind of nonconvex optimization problems, which often appear in various scientific and engineering applications, so they have great research value. Considering the shortcomings of the existing neural network model to solve the nonsmooth pseudoconvex optimization problem, a new single-layer recurrent neural network model based on differential inclusion theory is proposed. Through theoretical analysis, it is proved that the state solution of the neural network converges to the feasible region within a limited time and stays in it forever. Finally, the state solution of the neural network converges to the optimal solution of the original optimization problem. At the end of the article, the validity of the proposed theory is verified through numerical experiments. Compared with existing neural networks, the neural network model proposed in this paper is simple in structure, does not need to calculate penalty parameters in advance, and has no special requirements for the selection of initial points.
-
Key words:
- Neural network /
- Nonsmooth pseudoconvex optimization /
- Convergence /
- Optimal solution
-
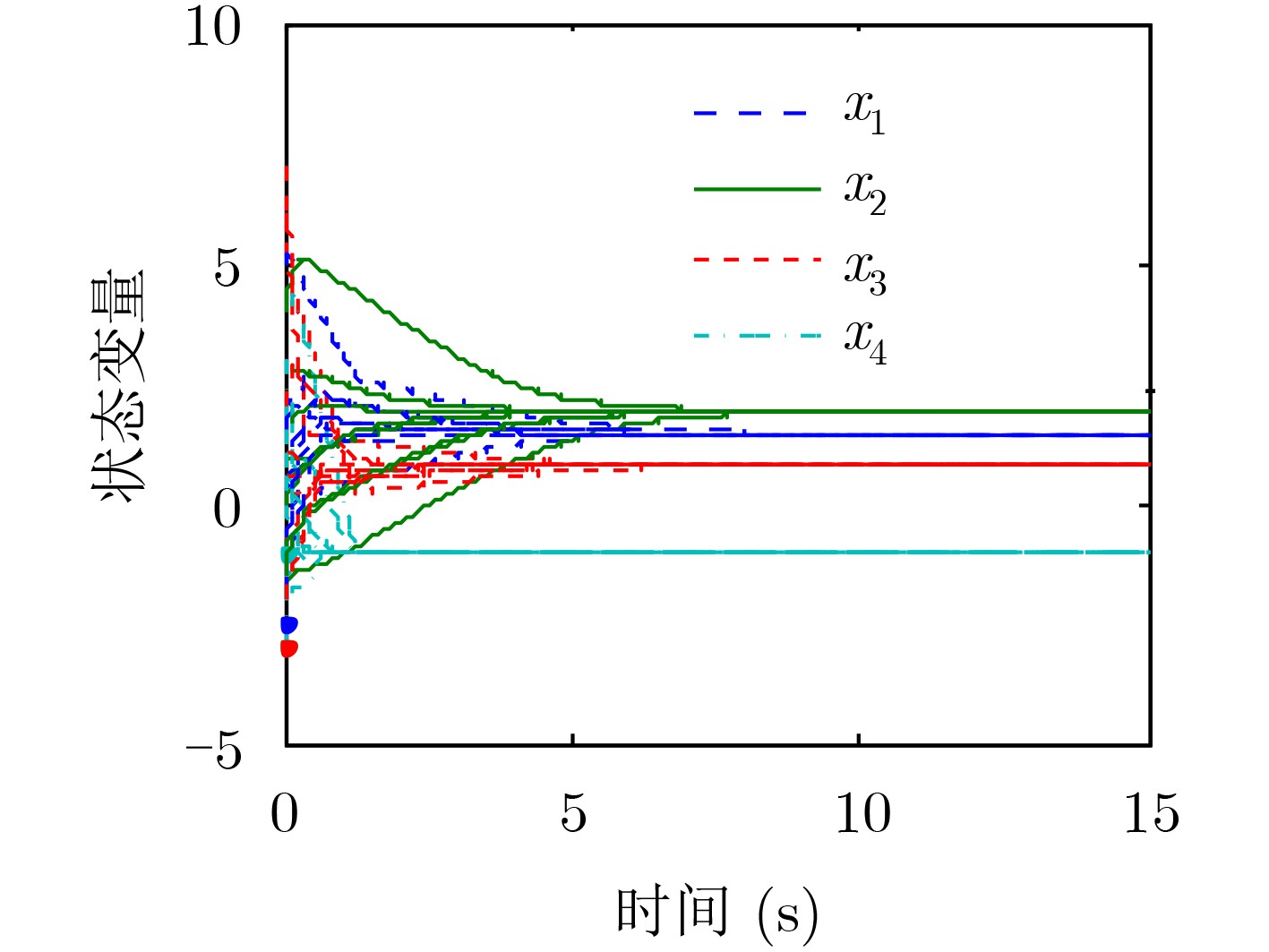
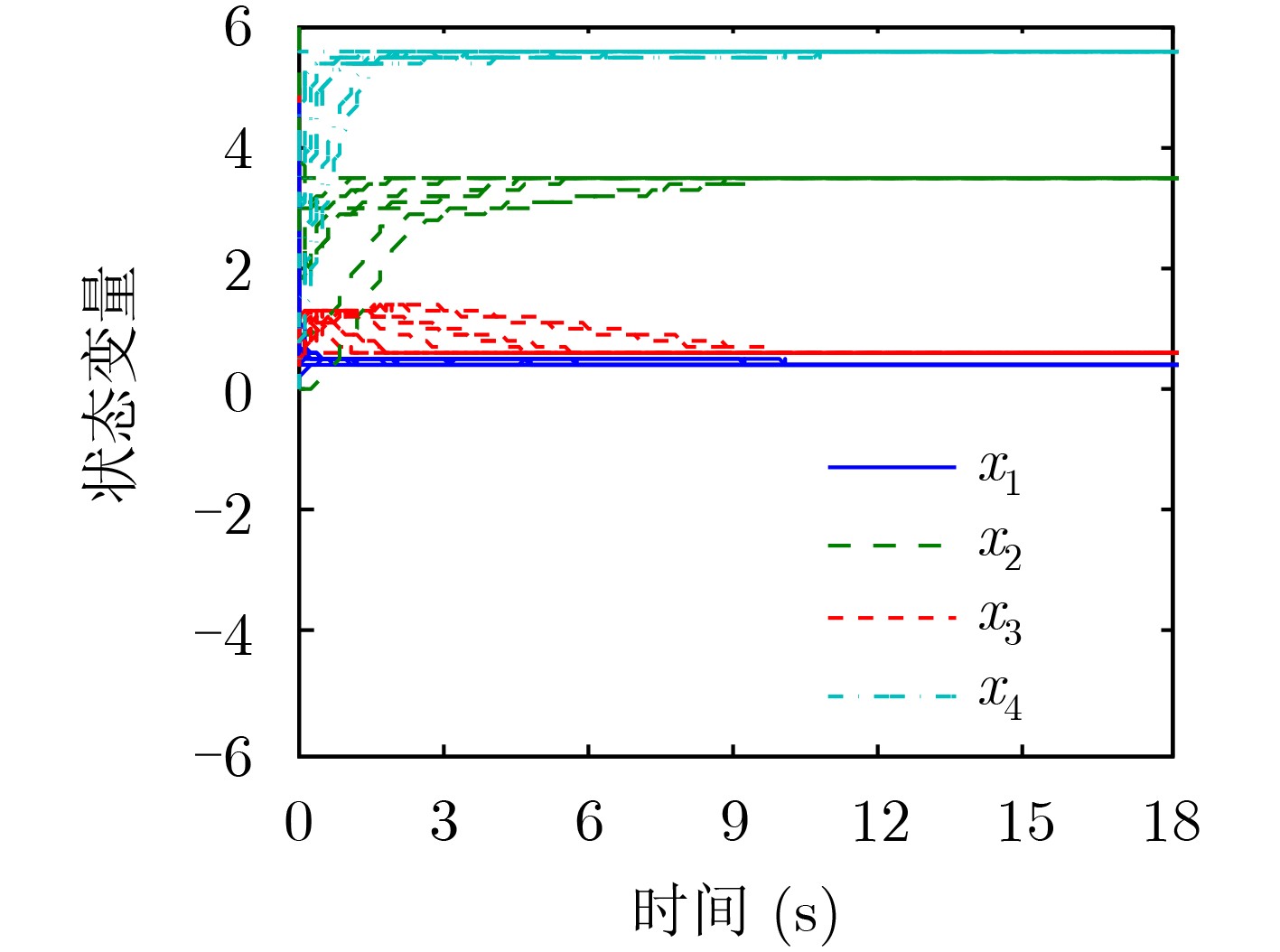
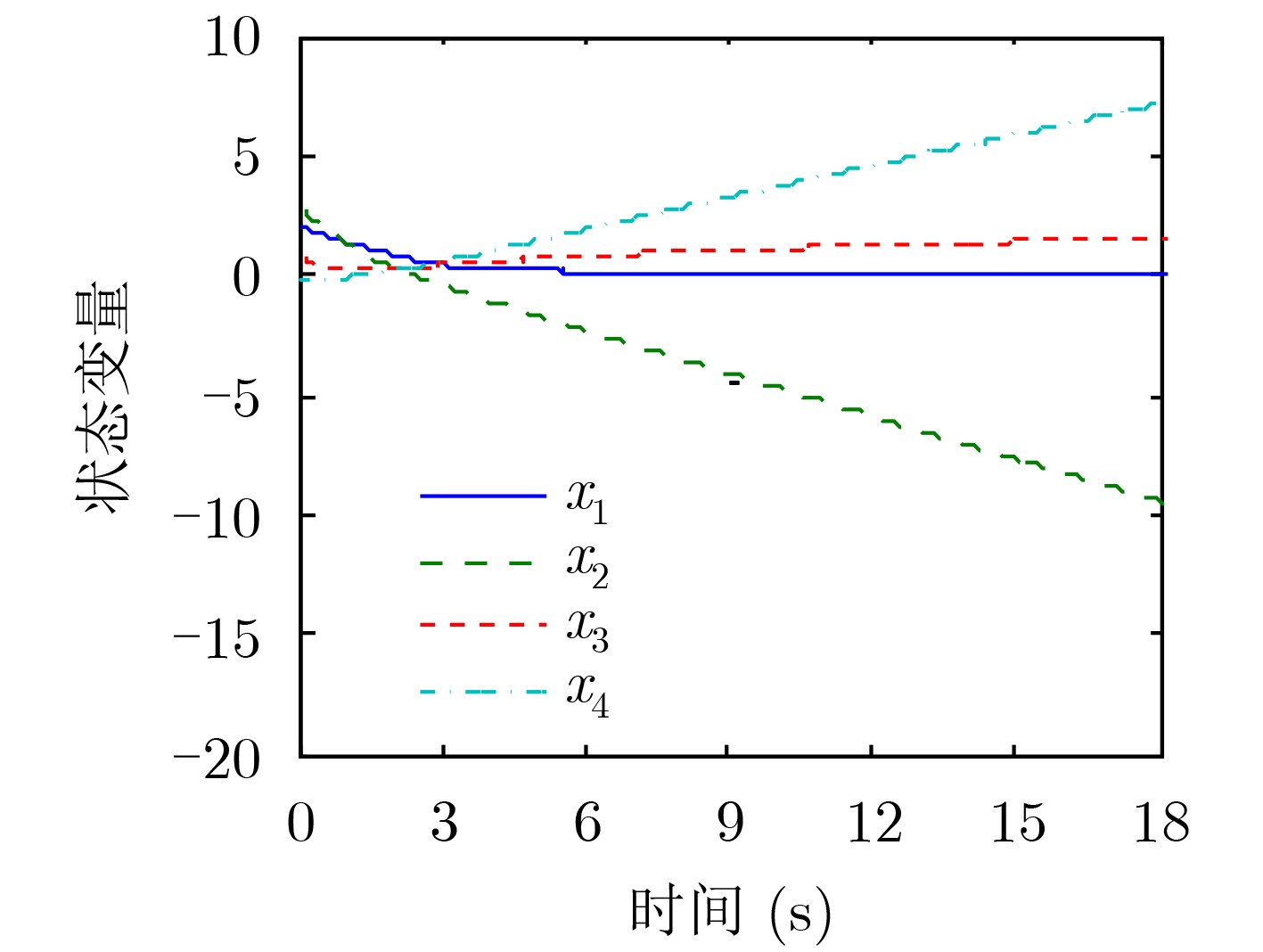
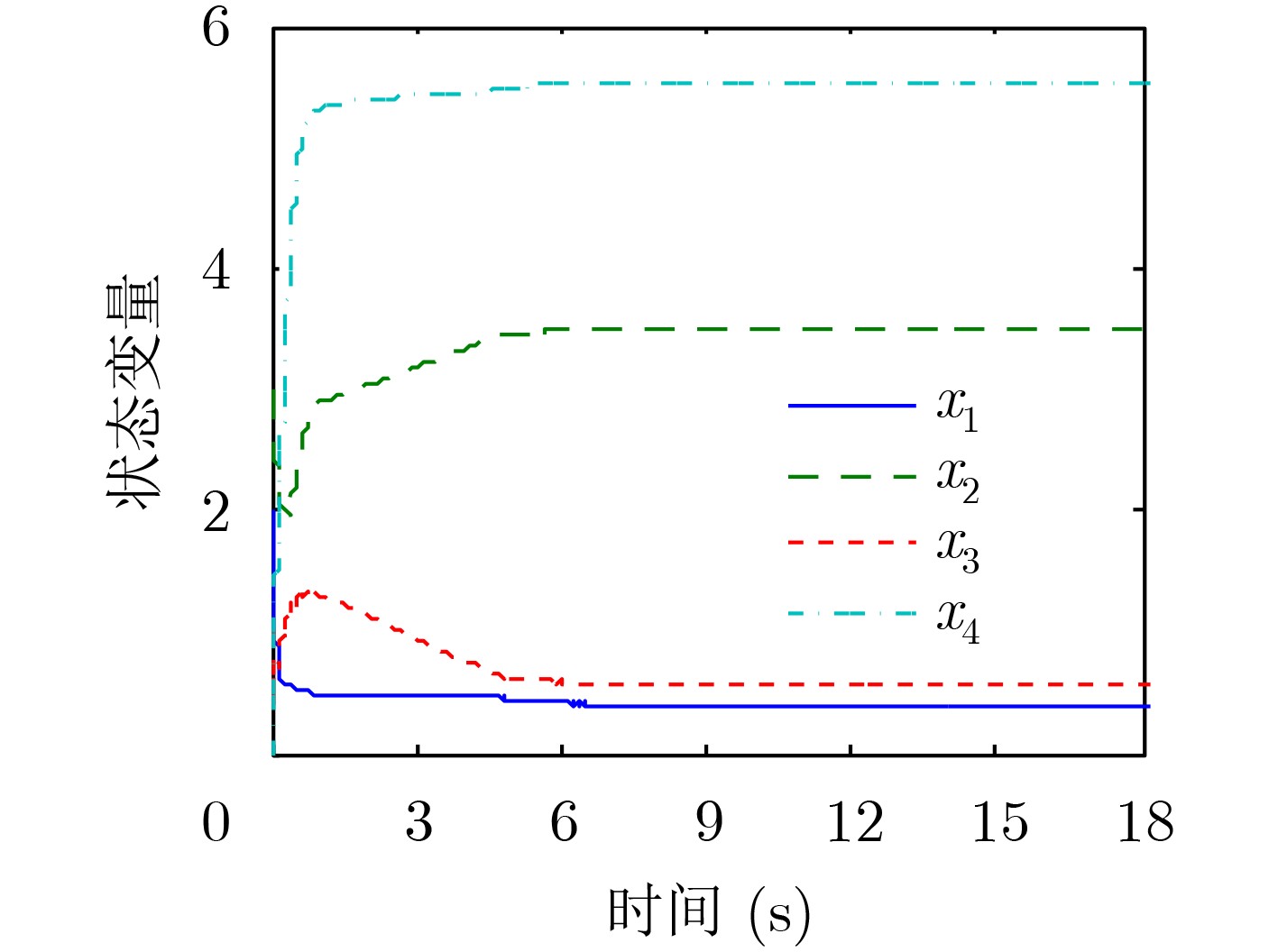
图 5 文献[10]中初始点为
${(2,3,1,0)^{\rm{T}}}$ 的收敛轨迹 -
[1] TANK D W and HOPFIELD J. Simple ‘neural’ optimization networks: An A/D converter, signal decision circuit, and a linear programming circuit[J]. IEEE Transactions on Circuits and Systems, 1986, 33(5): 533–541. doi: 10.1109/TCS.1986.1085953 [2] KENNEDY M P and CHUA L O. Neural networks for nonlinear programming[J]. IEEE Transactions on Circuits and Systems, 1988, 35(5): 554–562. doi: 10.1109/31.1783 [3] XUE Xiaoping and BIAN Wei. Subgradient-based neural networks for nonsmooth convex optimization problems[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(8): 2378–2391. doi: 10.1109/TCSI.2008.920131 [4] QIN Sitian, FAN Dejun, WU Guangxi, et al. Neural network for constrained nonsmooth optimization using Tikhonov regularization[J]. Neural Networks, 2015, 63: 272–281. doi: 10.1016/j.neunet.2014.12.007 [5] QIN Sitian and XUE Xiaoping. A two-layer recurrent neural network for nonsmooth convex optimization problems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(6): 1149–1160. doi: 10.1109/TNNLS.2014.2334364 [6] LI Qingfa, LIU Yaqiu, and ZHU Liangkuan. Neural network for nonsmooth pseudoconvex optimization with general constraints[J]. Neurocomputing, 2014, 131: 336–347. doi: 10.1016/j.neucom.2013.10.008 [7] LIU Qingshan, GUO Zhishan, and WANG Jun. A one-layer recurrent neural network for constrained pseudoconvex optimization and its application for dynamic portfolio optimization[J]. Neural Networks, 2012, 26: 99–109. doi: 10.1016/j.neunet.2011.09.001 [8] HOSSEINI A. A non-penalty recurrent neural network for solving a class of constrained optimization problems[J]. Neural Networks, 2016, 73: 10–25. doi: 10.1016/j.neunet.2015.09.013 [9] QIN Sitian, YANG Xiudong, XUE Xiaoping, et al. A one-layer recurrent neural network for pseudoconvex optimization problems with equality and inequality constraints[J]. IEEE Transactions on Cybernetics, 2017, 47(10): 3063–3074. doi: 10.1109/TCYB.2016.2567449 [10] BIAN Wei, MA Litao, QIN Sitian, et al. Neural network for nonsmooth pseudoconvex optimization with general convex constraints[J]. Neural Networks, 2018, 101: 1–14. doi: 10.1016/j.neunet.2018.01.008 [11] 高鑫, 李慧, 张义, 等. 基于可变形卷积神经网络的遥感影像密集区域车辆检测方法[J]. 电子与信息学报, 2018, 40(12): 2812–2819. doi: 10.11999/JEIT180209GAO Xin, LI Hui, ZHANG Yi, et al. Vehicle detection in remote sensing images of dense areas based on deformable convolution neural network[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2812–2819. doi: 10.11999/JEIT180209 [12] LIU Na and QIN Sitian. A neurodynamic approach to nonlinear optimization problems with affine equality and convex inequality constraints[J]. Neural Networks, 2019, 109: 147–158. doi: 10.1016/j.neunet.2018.10.010 [13] YU Xin, WU Lingzhen, XU Chenhua, et al. A novel neural network for solving nonsmooth nonconvex optimization problems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(5): 1475–1488. doi: 10.1109/TNNLS.2019.2920408 [14] LI Wenjing, BIAN Wei, and XUE Xiaoping. Projected neural network for a class of Non-Lipschitz optimization problems with linear constraints[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(9): 3361–3373. doi: 10.1109/TNNLS.2019.2944388 [15] XU Chen, CHAI Yiyuan, QIN Sitian, et al. A neurodynamic approach to nonsmooth constrained pseudoconvex optimization problem[J]. Neural Networks, 2020, 124: 180–192. doi: 10.1016/j.neunet.2019.12.015 [16] 喻昕, 许治健, 陈昭蓉, 等. 拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题[J]. 电子与信息学报, 2017, 39(8): 1950–1955. doi: 10.11999/JEIT161049YU Xin, XU Zhijian, CHEN Zhaorong, et al. Lagrange neural network for nonsmooth nonconvex optimization problems with equality and inequality constrains[J]. Journal of Electronics &Information Technology, 2017, 39(8): 1950–1955. doi: 10.11999/JEIT161049 [17] CHENG Long, HOU Zengguang, LIN Yingzi, et al. Recurrent neural network for non-smooth convex optimization problems with application to the identification of genetic regulatory networks[J]. IEEE Transactions on Neural Networks, 2011, 22(5): 714–726. doi: 10.1109/TNN.2011.2109735 [18] BIAN Wei and XUE Xiaoping. Subgradient-based neural networks for nonsmooth nonconvex optimization problems[J]. IEEE Transactions on Neural Networks, 2009, 20(6): 1024–1038. doi: 10.1109/TNN.2009.2016340 [19] LIU Qingshan and WANG Jun. A one-layer recurrent neural network for constrained nonsmooth optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) , 2011, 41(5): 1323–1333. doi: 10.1109/TSMCB.2011.2140395 [20] QIN Sitian, FAN Dejun, SU Peng, et al. A simplified recurrent neural network for pseudoconvex optimization subject to linear equality constraints[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(4): 789–798. doi: 10.1016/j.cnsns.2013.08.034 [21] QIN Sitian, BIAN Wei, and XUE Xiaoping. A new one-layer recurrent neural network for nonsmooth pseudoconvex optimization[J]. Neurocomputing, 2013, 120: 655–662. doi: 10.1016/j.neucom.2013.01.025 [22] AUBIN J P and CELLINA A. Differential Inclusions[M]. Berlin, Germany: Springer-Verlag, 1984: 77. -





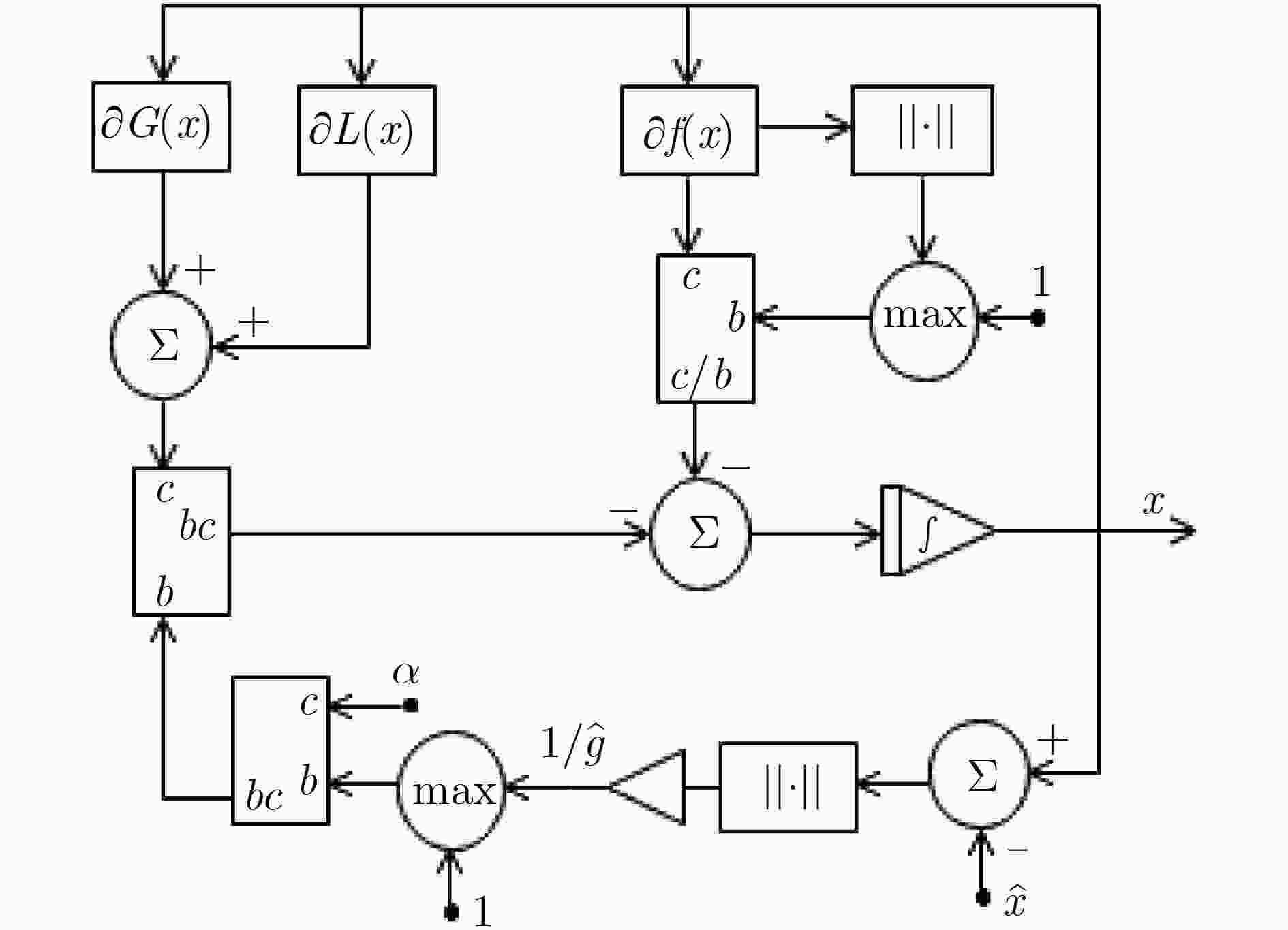
 下载:
下载:




 下载:
下载:
