A New Coprime Array with High Degree of Freedom Based on the Difference and Sum Co-array
-
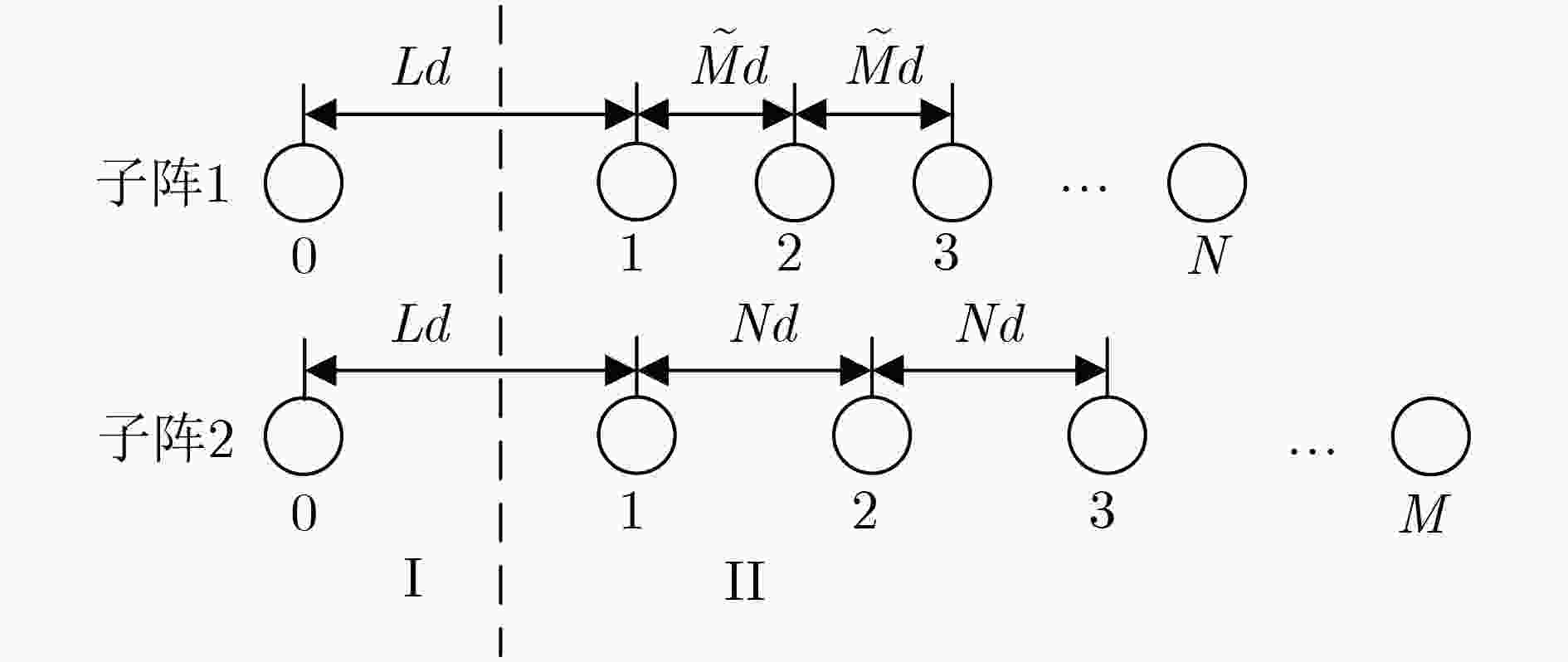
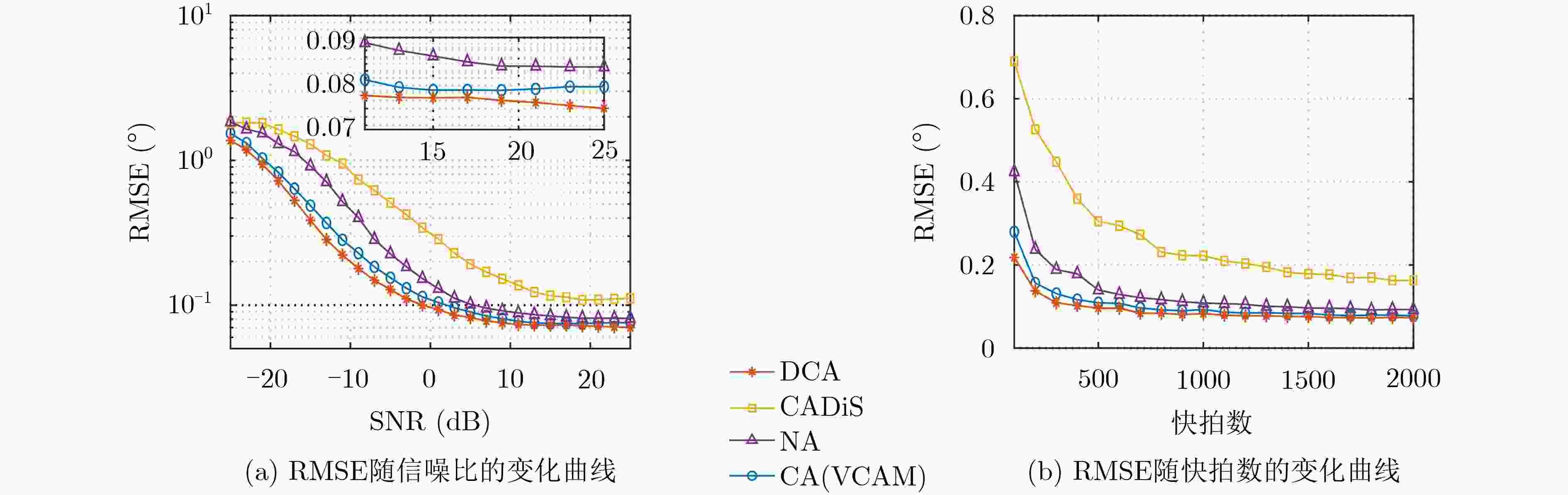
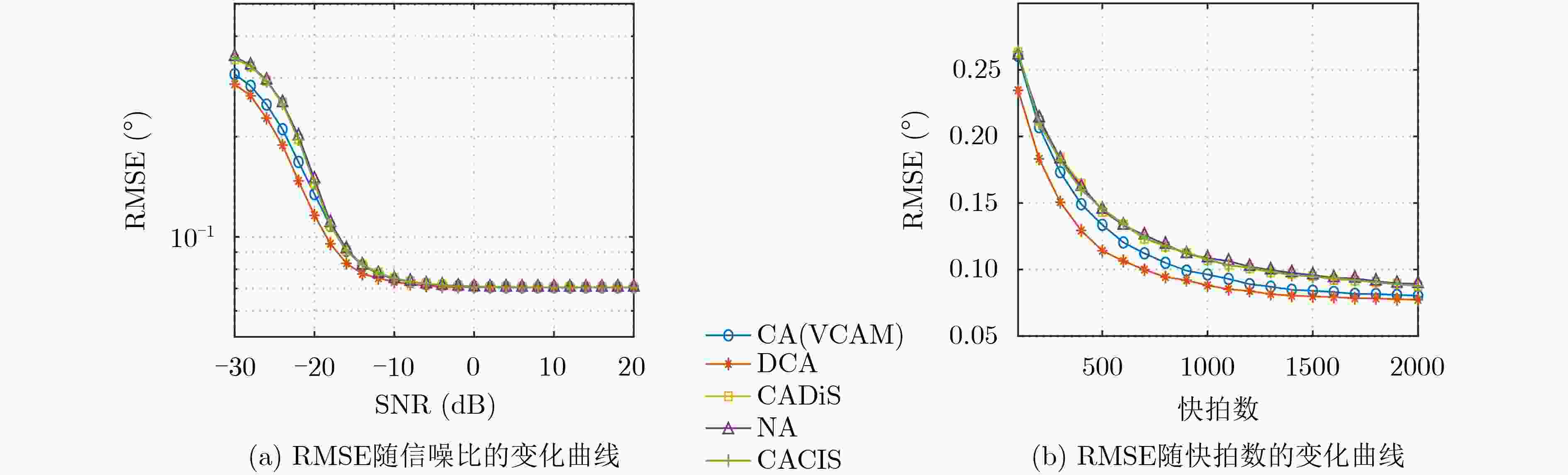
摘要: 针对均匀线列阵自由度(DOF)受限于阵元数的问题,该文提出一种基于差和共阵的新型互质阵,称为放置互质阵(DCA),其借助由接收信号的时域和空域信息组合成的共轭增广矩阵得到等价的差和共阵来进行波达方向(DOA)估计。DCA将广义互质阵放置在与原点处单阵元相隔一定距离的位置,实现了和共阵与差共阵的阵元位置互补,从而最大限度上利用和共阵带来的自由度增幅。该文给出了DCA阵元位置和放置距离的闭式表达,随后分别对DCA的差共阵及和共阵的连续阵元及孔洞位置进行了理论分析,同时给出了两者间的关系,说明了DCA的高自由度特性。多个仿真实验验证了所提阵型DOA估计的有效性。Abstract: To deal with the problem that the Degree Of Freedom(DOF) of uniform linear array is limited by the number of elements, a new type of coprime array is proposed called Displaced Coprime Array(DCA).It takes use of the conjugate augmented matrix which is formed by the time and space information of the received signal to obtain the equivalent difference and sum co-array and to estimate the Direction Of Arrival(DOA). DCA places the generalized coprime array at a certain distance from the single array element at the coordinate origin so that the elements of the sum co-array and the difference co-array are complemented. As a result, the use of DOF provided by the sum co-array can be maximized. In this paper, the closed-form expressions of the element positions and the placement distance of DCA are given. Then, the performance of the sum co-array and the difference co-array including the continuous elements and the hole positions is theoretically analyzed, the relationship between the two is given and high DOF of DCA is presented. Multiple simulations verify the effectivity of DOA estimation using DCA.
-
表 1 两种阵型的最优设计及最大自由度
阵型 表达式 子阵阵元数最优选择 最大自由度 DCA $P = M + N$
${\rm{DOF}} = 2MN - N + 1$$P$为偶,$P/2$为偶:$M = P/2 + 1,N = P/2 - 1$ $({P^2} - P)/2$ $P$为偶,$P/2$为奇:$M = P/2 + 2,N = P/2 - 2$ $({P^2} - P - 10)/2$ $P$为奇:$M = (P + 1)/2,N = (P - 1)/2$ $({P^2} - P + 2)/2$ CA(VCAM) $P = M + N - 1$
${\rm{DOF}} = MN + M + N - 1$$P$为偶:$M = (P + 2)/2,N = P/2$ $({P^2} + 6P)/4$ $P$为奇,$(P + 1)/2$为偶:$M = (P + 1)/2 + 1,N = (P + 1)/2 - 1$ $({P^2} + 6P - 3)/4$ $P$为奇,$(P + 1)/2$为奇:$M = (P + 1)/2 + 2,N = (P + 1)/2 - 2$ $({P^2} + 6P - 15)/4$ 表 2 各阵型同孔径下的阵型配置
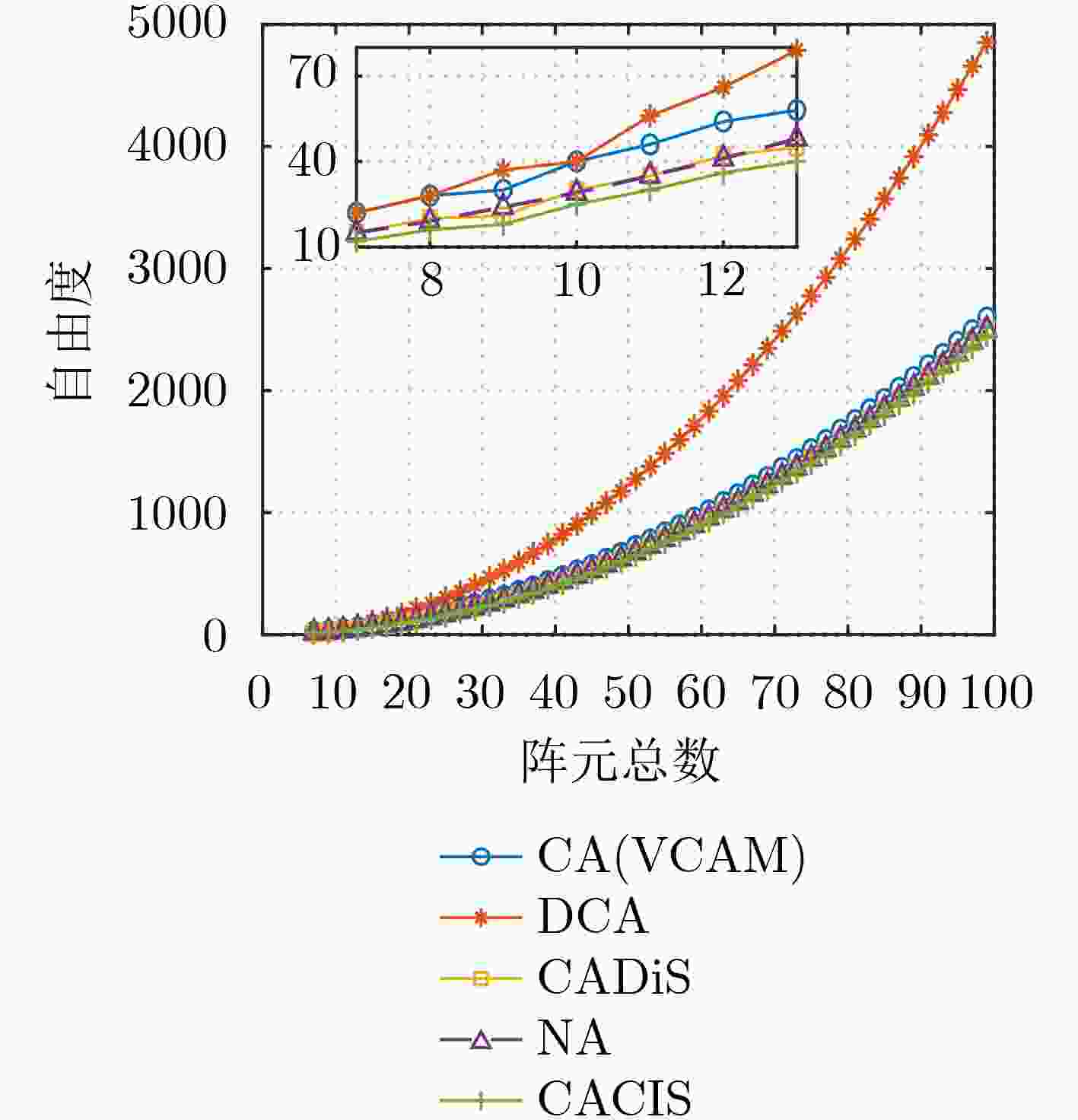
阵型 阵元总数 子阵阵元数 孔径 自由度 CACIS 27 $(M,N) = (15,13)$ 182 182 CA(VCAM) 27 $(M,N) = (15,13)$ 182 222 CADiS 26 $(M,N) = (14,13)$ 182 182 NA 26 $({N_1},{N_2}) = (13,13)$ 181 181 DCA 23 $(M,N) = (12,11)$ 182 254 -
YANG Jie, YANG Yixin, LEI Bo, et al. Nonuniform linear array DOA estimation using EM criterion[J]. Digital Signal Processing, 2019, 86: 36–41. doi: 10.1016/j.dsp.2018.12.010 QIN Guodong, AMIN M G, and ZHANG Y D. DOA estimation exploiting sparse array motions[J]. IEEE Transactions on Signal Processing, 2019, 67(11): 3013–3027. doi: 10.1109/TSP.2019.2911261 鄢社锋. 优化阵列信号处理(上册)[M]. 北京: 科学出版社, 2018: 1–31.YAN Shefeng. Optimal Array Signual Pocssing: Beamformer Design Theory and Methods[M]. Beijing: Science Press, 2018: 1–31. HOCTOR R T and KASSAM S A. The unifying role of the coarray in aperture synthesis for coherent and incoherent imaging[J]. Proceedings of the IEEE, 1990, 78(4): 735–752. doi: 10.1109/5.54811 MOFFET A T. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(2): 172–175. doi: 10.1109/TAP.1968.1139138 LIU Chunlin and VAIDYANATHAN P P. Remarks on the spatial smoothing step in coarray MUSIC[J]. IEEE Signal Processing Letters, 2015, 22(9): 1438–1442. doi: 10.1109/lsp.2015.2409153 PAL P and VAIDYANATHAN P P. Coprime sampling and the music algorithm[C]. 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, USA, 2011: 289–294. doi: 10.1109/DSP-SPE.2011.5739227. BLOOM G S and GOLOMB S W. Applications of numbered undirected graphs[J]. Proceedings of the IEEE, 1977, 65(4): 562–570. doi: 10.1109/PROC.1977.10517 PAL P and VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167–4181. doi: 10.1109/tsp.2010.2049264 LIU Chunlin and VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part I: Fundamentals[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997–4012. doi: 10.1109/TSP.2016.2558159 LIU Chunlin and VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part II: High-order extensions[J]. IEEE Transactions on Signal Processing, 2016, 64(16): 4203–4217. doi: 10.1109/TSP.2016.2558167 LIU Chunlin and VAIDYANATHAN P P. Hourglass arrays and other novel 2-D sparse arrays with reduced mutual coupling[J]. IEEE Transactions on Signal Processing, 2017, 65(13): 3369–3383. doi: 10.1109/TSP.2017.2690390 VAIDYANATHAN P P and PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573–586. doi: 10.1109/TSP.2010.2089682 李建峰, 沈明威, 蒋德富. 互质阵中基于降维求根的波达角估计算法[J]. 电子与信息学报, 2018, 40(8): 1853–1859. doi: 10.11999/JEIT171087LI Jianfeng, SHEN Mingwei, and JIANG Defu. Reduced-dimensional root finding based direction of arrival estimation for coprime array[J]. Journal of Electronics &Information Technology, 2018, 40(8): 1853–1859. doi: 10.11999/JEIT171087 AHMED A, ZHANG Y D, and ZHANG Jiankang. Coprime array design with minimum lag redundancy[C]. ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, United Kingdom, 2019: 4125–4129. doi: 10.1109/ICASSP.2019.8683315. 冯明月, 何明浩, 陈昌孝, 等. 基于Bessel先验快速稀疏贝叶斯学习的互质阵列DOA估计[J]. 电子与信息学报, 2018, 40(7): 1604–1611. doi: 10.11999/JEIT170951FENG Mingyue, HE Minghao, CHEN Changxiao, et al. DOA estimation for co-prime array based on fast sparse Bayesian learning using Bessel priors[J]. Journal of Electronics &Information Technology, 2018, 40(7): 1604–1611. doi: 10.11999/JEIT170951 QIN Si, ZHANG Y D, and AMIN M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377–1390. doi: 10.1109/TSP.2015.2393838 ZHANG Yankui, XU Haiyun, ZONG Rong, et al. A novel high degree of freedom sparse array with displaced multistage cascade subarrays[J]. Digital Signal Processing, 2019, 90: 36–45. doi: 10.1016/j.dsp.2019.04.005 RAZA A, LIU Wei, and SHEN Qing. Thinned coprime array for second-order difference co-array generation with reduced mutual coupling[J]. IEEE Transactions on Signal Processing, 2019, 67(8): 2052–2065. doi: 10.1109/TSP.2019.2901380 孙兵, 阮怀林, 吴晨曦, 等. 基于Toeplitz协方差矩阵重构的互质阵列DOA估计方法[J]. 电子与信息学报, 2019, 41(8): 1924–1930. doi: 10.11999/JEIT181041SUN Bing, RUAN Huailin, WU Chenxi, et al. Direction of arrival estimation with coprime array based on Toeplitz covariance matrix reconstruction[J]. Journal of Electronics &Information Technology, 2019, 41(8): 1924–1930. doi: 10.11999/JEIT181041 WANG Xinghua, CHEN Zhenhong, REN Shiwei, et al. DOA estimation based on the difference and sum coarray for coprime arrays[J]. Digital Signal Processing, 2017, 69: 22–31. doi: 10.1016/j.dsp.2017.06.013 SHAN Zhilong and YUM T S P. A conjugate augmented approach to direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2005, 53(11): 4104–4109. doi: 10.1109/tsp.2005.857012 SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 CHEN Zhenhong, DING Yingtao, REN Shiwei, et al. A novel nested configuration based on the difference and sum co-array concept[J]. Sensors, 2018, 18(9): 2988. doi: 10.3390/s18092988 SHEN Qing, LIU Wei, CUI Wei, et al. Extension of nested arrays with the fourth-order difference co-array enhancement[C]. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 2016: 2991–2995. doi: 10.1109/ICASSP.2016.7472226. -





 下载:
下载:




 下载:
下载:
