Review of SoC Estimation Methods for Electric Vehicle Li-ion Batteries
-
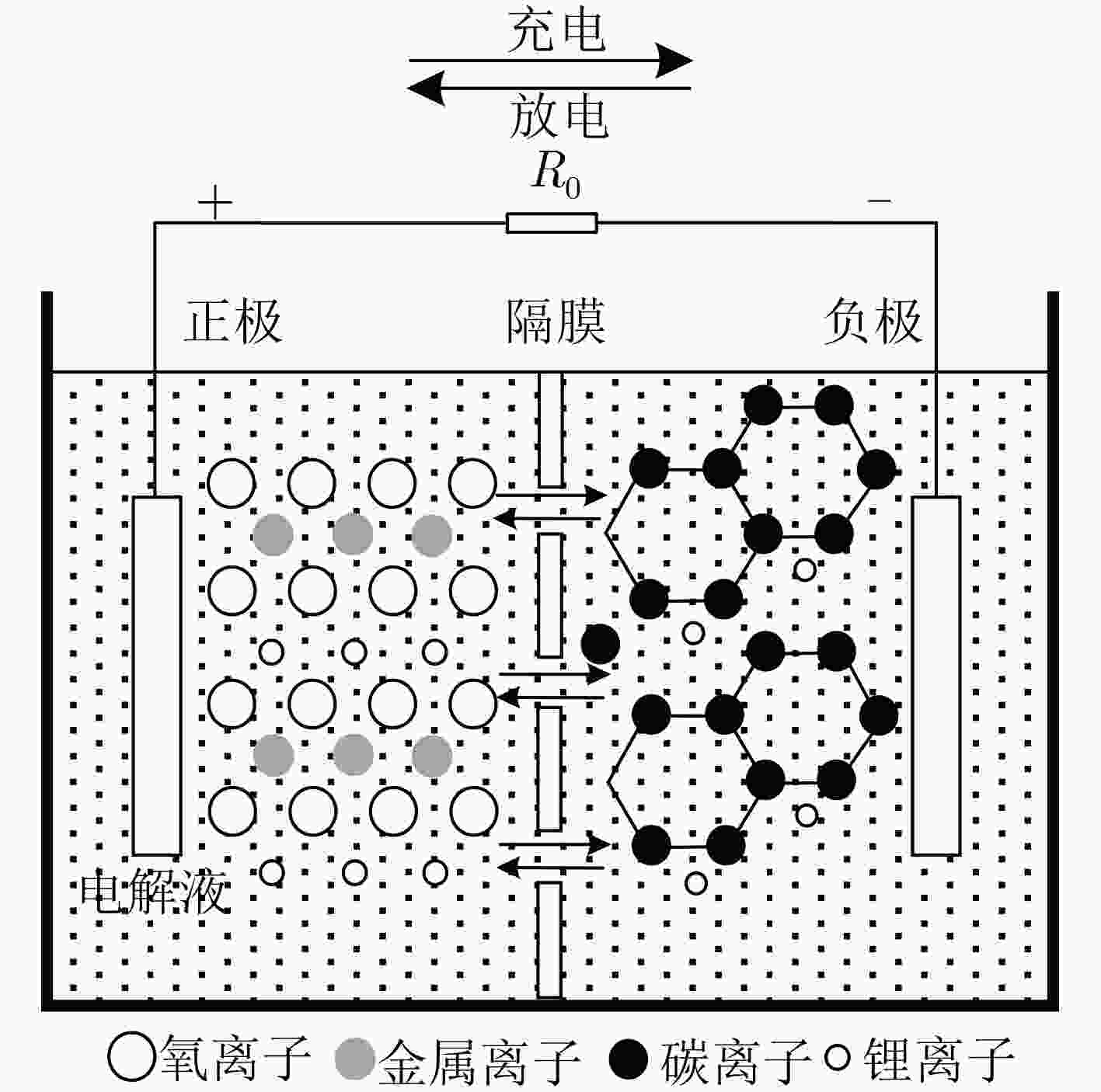
摘要: 锂离子电池具有循环寿命长、能量密度高、自放电率低、环境污染小等优点，在电动汽车产业中得到广泛应用。电动汽车中的电池管理系统(BMS)可以维护和监测电池状态，确保电池的安全性和可靠性。电池荷电状态(SoC)表示电池中剩余的电量，是BMS的重要参数之一，实时精确的SoC估算可以延长电池寿命，保障行驶安全。然而锂离子电池是一个高度复杂的非线性时变系统，电池寿命、环境温度、电池自放电等许多未知因素均会对估算精度造成影响，使估算难度大大增加。为了满足不同条件下对锂离子电池SoC精确、快速、实时估算的要求，需要对SoC估计算法进行进一步研究与改进。近年来已有相关文献对锂离子电池SoC的估算方法进行了综述，然而已有相关综述对估算方法的总结不够全面且缺少流程表达。该文首先介绍了锂离子电池的工作原理，阐述了影响电池SoC估算的因素；其次，通过总结最新的研究成果对电池SoC估算方法进行了归纳分析，根据各类算法的不同特性将其分为查表法、安时积分法、基于模型的方法、数据驱动的方法以及混合方法五大类，说明了各类估算方法的主要特征并对模型或算法的优缺点进行综合的比较和讨论；最后，对电动汽车中锂离子电池SoC估算方法的未来发展方向做出展望。Abstract: Lithium-ion battery has been widely used in electric vehicle industry because of its long cycle life, high energy density, low self-discharge rate and low environmental pollution. The Battery Management System (BMS) in electric vehicles can maintain and monitor the battery status to ensure the security and reliability of the battery. The battery’s State of Charge (SoC) represents the remaining power in the battery and is one of the important parameters of the BMS. Real-time and accurate SoC estimation can extend battery life and ensure driving safety. However, Lithium-ion battery is indeed a highly complex nonlinear time-varying system, many unknown factors, such as battery life, ambient temperature, battery self-discharge and so on, will affect the estimation accuracy, which greatly increases the difficulty of estimation. To meet the requirements of accurate, rapid and real-time SoC estimation for Lithium-ion batteries under different conditions, further research and improvement of SoC estimation algorithm are needed. In recent years, some review literature on the Lithium-ion battery SoC estimation has been published. However, the existing literature has not summarized the estimation methods comprehensively and lack of process description. In this paper, the working principle of Lithium-ion battery is firstly introduced, as well as the factors affecting the SoC estimation of battery. Secondly, summary and analysis of the battery SoC estimation methods are conducted by the latest research achievement. According to the different characteristics of various algorithms, the battery SoC estimation can be divided into five categories: look-up table method, ampere hour integration method, model-based method, data-driven method and hybrid method. The main characteristics of various estimation methods are explained and the advantages and disadvantages of models or algorithms are comprehensively compared and discussed. Finally, the future development direction of SoC estimation methods for Lithium-ion batteries in electric vehicles is prospected.
-
1. 引言
在数据传输过程中，不仅要保护数据的机密性，而且还要保证数据的不可伪造性。1997年，Zheng[1]提出签密的概念。签密可以同时完成“签名和加密”功能，该技术与传统的先加密后签名或者先签名后加密相比具有通信成本低、安全水平高等优点，在很多实际应用场景中受到青睐[2, 3]。2009年Selvi等人[4]结合了聚合签名和签密的优势，提出了聚合签密概念。
聚合签密可以把多个签密密文聚合为单个签密密文，验证者仅需验证聚合后的密文，就可以实现对多个消息的认证。聚合签密适合于多对一的用户环境，在无线传感器[5]等领域得到了广泛的使用。随后，Han等人[6]提出了基于身份的聚合签密的方案，Eslami等人[7]提出了基于无证书的聚合签密方案。在实际应用环境中，跨平台通信越来越普及，不同系统使用不同的密码系统，为了保证异构密码系统之间数据的机密性和完整性。2010年，Sun等人[8]首次提出了异构签密方案。随后，Huang等人[9]提出了一个从传统公钥密码体制(Traditional Public Key Cryptography, TPKC)到身份公钥密码体制(IDentity-based Public Key Cryptographic, IDPKC) TPKI→IDPKC异构签密方案，Li等人[10]提出了IDPKC→TPKI签密方案。自此，异构签密成为当前密码学研究的一个热点[11—15]。
2017年，Niu等人[16]提出了一个具有隐私保护功能的异构聚合签密方案，经过分析，发现该方案不满足签密密文的不可伪造性。恶意密钥生成中心(Key Generating Center, KGC)可以伪造签密密文。为了解决Niu方案[16]中存在的密文可伪造攻击，本文先提出了一种新的具有系统隐私功能的保护异构聚合签密方案，随后证明了本文方案的安全性。最后对比了本文方案与Niu方案。
2. Niu方案及安全性分析
限于篇幅，略去对Niu方案的描述，具体算法见文献[16]。
Niu方案是从无证书公钥密码体制到身份公钥密码体制(CLPKC→IDPKC)的异构签密方案。对于机密性，主要考虑IDPKC密码环境；对于不可伪造性，则是CLPKC密码环境。在CLPKC中，主要存在两类敌手A1和A2。A1为不诚实的用户，通过对用户原有公钥的替换实现公钥替换攻击；A2为恶意的KGC，可以获取系统的主密钥和用户的部分私钥，实现KGC攻击。通过分析，发现Niu方案不满足密文的不可伪造性，即KGC可以伪造单个签密密文和聚合签密密文。
2.1 单个签密密文伪造
KGC 通过以下过程实现单个密文的伪造：(1)KGC在系统初始化时，选择
¯w∈Z∗q ，计算Q=¯wP 作为G1 的一个生成元。随机选择s∈Z∗q 为系统的主密钥，计算Ppu=sP 为系统公开密钥。(2) KGC随机选择
r′j∈Z∗q ，计算r′jQ=R′j¯w 和h′j=H4(Cj,R′j,Psj,IDsj) ，可计算出Xsj¯wP=Psj¯w 。(3)伪造签密密文：
Sj=Dsj+h′jr′j¯wP+Psj¯w ，则伪造的密文为σj= (Rj,Cj,Sj,Γj) 。(4)验证伪造密文的正确性：由于
e(S′j,P)=e(Dsj+h′jr′j¯wP+Psj¯w,P)=e(Dsj,P)e(h′jr′j¯wP,P)e(Psj¯w,P)=e(s⋅Qsj,P)e(h′jr′jP,Q)e(Psj,Q)=e(Qsj,Ppu)e(h′jR′j+Psj,Q) 因此，KGC可以成功伪造单个签密密文。
2.2 聚合签密密文伪造
KGC通过以下过程实现聚合密文的伪造：
(1)按照2.1节步骤伪造单个密文。
(2)
S=∑mj=1Sj=∑mj=1(Dsj+XsjQ+h′jr′jQ) ，伪造聚合签密密文为σj=({Rj,Cj,Γj}mj=1,S) 。(3)验证伪造密文的正确性：由于
e(S,P)=e(m∑j=1(Dsj+XsjQ+h′jr′jQ),P)=e(m∑j=1Dsj,P)e(m∑j=1XsjQ,P)⋅e(m∑j=1h′jr′jQ,P)=e(m∑j=1Qsj⋅s,P)e(m∑j=1XsjQ,P)⋅e(m∑j=1h′jR′j,Q)=e(m∑j=1Qsj,Ppu)e(m∑j=1Psj,Q)⋅e(m∑j=1h′jr′j,Q)=e(m∑j=1Qsj,Ppu)e(m∑j=1(Psj+h′jr′j),Q) 因此，KGC可以成功伪造聚合签密密文。
3. 改进的异构签密方案
Niu方案的主要问题在于签密生成环节泄漏了签密者的秘密值信息，即KGC可以容易地得到
XsjQ 和r′jQ 。(1) 系统建立Setup：输入安全参数
k ,KGC 选择两个阶为q 的循环群G1 和G2 ,G1 为加法群，G2 为循环乘群。P 为G1 的生成元。e:G1×G1→G2 为一个双线性映射。KGC 随机地选择s∈Z∗q 作为系统的主密钥，保留s 。计算系统公钥为Ppu=sP 。KGC 选择4个哈希函数H1:{0,1}∗→G1 ,H2:G2→ {0,1}lm ,H3:{0,1}∗→Z∗q ,H4:{0,1}lm→G1 。系统参数params={q,G1,G2,e,P,Ppu,H1,H2,H3,H4} 。(2) 公/私钥生成CLPKC-KG: CLPKC系统中发送者
Si(i∈{1,2,···,n}) 的身份为Mj 。(3) 密钥提取IDPKC-KG: IDPKC系统中接收者的身份为
IDrj(j∈{1,2,···,n}) 。CLPKC-KG和IDPKC-KG里面包含的算法设置同2.1节。(4) 签密Signcrypt：输入消息
Mi 和接收者的身份列表L={IDri}ni=1 ，发送者Sj 执行如下步骤：(a)随机地选择
ri∈Z∗q ，计算Ri=riP ,ωi= e(Ppu,Pi)ri和Ci=H2(ωi)⊕Mi 。(b)对
j=1,2,···,m ，计算xrj=H3(IDrj) ,fj(x)= ∏1≤j≠i≤mx−xixj−xi=aj,1+aj,2x+aj,mxm−1 ,yji=ri(Pi+ Qrj) ，其中aj,1,aj,2,···,aj,m∈Z∗q 。(c)对于
j=1,2,···,m ，计算Tji=∑nk=1ak,jyk,i ，令Γ=(T1i,T2i,···,Tmi) 。(d)计算
hi=H3(Ci,Ri,Psi,IDsi) 和Si=Dsi+(Xsi+ hiri)H4(Ppu) 。(e)发送者
Si 把密文σi=(Ri,Ci,Si,Γi) 给接收者。(5) 单个解签密Individual De-signcrypt：收到密文
σi=(Ri,Ci,Si,Γi)}mi=1 ，接收者利用自己的身份IDrj(j∈{1,2,···,n}) 解密σi 步骤如下：(a)计算
Qsi=H1(IDsi) ,hi=H3(Ci,Ri,Pi,IDi) 。(b)检查
e(Si,P)=e(Qsi,Ppu)e(Psi+hi⋅Ri,H4(Q)) 是否成立。如果成立，密文有效；否则，拒绝该密文。(c)计算
xj=H3(IDrj) 和y′ij =T1i+xjT2i+··· +xm−1jTmi (i=1,2,···,n) 。(d)计算
ω′i=e(Ppu,y′ij)e(Ri,Drj)−1 。(e)恢复消息
Mi ,Mi=H2(ωi)⊕Ci(i=1,2,···,m) 。(6) 聚合签密Aggregate：由聚合者执行产生
m 个用户对M 个消息的聚合签密过程如下：(a)输入
{IDsi}mi=1 签密密文σi=(Ri,Ci,Si,Γi)mi=1 。(b)计算
S=m∑i=1Si 。(c)输出聚合密文为
σ=({Ri,Ci,Γi}mi=1,S) 。(7)聚合验证Aggregate de-signcrypt：验证聚合签密是否有效，步骤如下：
(a)计算
Qsi=H1(IDsi),hi=H3(Ci,Ri,Psi,IDsi) 。(b)检查等式
e(S,P)=e(m∑i=1Qsi,Ppu)e(m∑i=1(Psi+hi⋅Ri),H4(Q)) 是否成立。成立则接受；否则，退出算法。4. 新方案的安全性分析
新方案的机密性证明过程与原方案一致，以下对不可伪造性进行分析。
4.1 单个签密密文不可伪造性
定理 1 假定CDH问题困难，针对敌手A1，本文异构签密方案在随机预言模型下自适应选择消息攻击下不可伪造。
以下需要引理1和引理2来证明定理1。
引理 1 在随机预言模型下，假设一个敌手A1在t时间内能以不可忽略的优势
ε 攻破本文方案，则存在算法B，能以ε′≥(ε−qs/2k)(1−1/qpk)qPk 优势解决 CDH 问题，其中，H1-Query, H2-Query, H3-Query, H4-Query, Partial-Private-Key-query, Secret-Value-query, Public-key-replave-query, Signcryption-query的访问次数分别为{q_{_H_1}} ,{q_{_H_2}} ,{q_{_H_3}} ,{q_{_H_4}} ,qpk ,qSk ,qkr ,qs 。证明 A1为攻击者，B为CDH问题的挑战者。B给定
(P,aP,bP) , B的目标是使用A1解决 CDH问题，即计算abP 。(1) 系统建立Setup：挑战者B设
Ppu=aP 。返回系统参数params 给A1, B随机选择挑战的伪身份ID∗ai , A1执行以下询问：(2)H1-query: B维持列表
L1=(IDsi,Qsi,αi,ci) ，初始为空。当A1对H1 进行询问时，B首先检查L1 列表，若列表L1 中存在(IDsi,Qsi,αi) ，B就返回相应的Qsi ，否则：B随机选择αi∈Z∗q 和ci∈{0,1} (其中，ci=0 的概率为ζ=1/qH1 。ci=1 的概率为1−ζ )。当ci=0 时，计算Qsi=αiP 。当ci=1 时，计算Qsi=αibP 。返回Qsi 给A1，并增加(IDsi,Qsi,αi,ci) 到L1 列表。(3) H2-query: B维持
L2=(ωi,ω2i,H2(ωi)) ，当B收到对H2 的询问时，B随机选择ω2i∈Z∗q ，令H2(ωi)=ω2i ，发送给A1。(4) H3-query: B维持
L3={Ci,Ri,Psi,IDsi,hi,γi} ，初始为空。当A1询问L3 列表的元组时，B首先检查列表，若列表中有相应元组，则发送对应的hi ；否则B随机选择γi∈Z∗q ，令hi=γi ，增加(Ci,RiPsi, IDsi,hi,γi) 到列表L3 中，并返回hi 。(5) H4-query: A1对
H4(Ppu) 进行询问时，B随机选择t∈Z∗q ，令H4(Ppu)=tP 。(6) 部分私钥询问Partial-Private-Key-query: B保持列表
E={IDsi,Dsi,Qsi} ，初始为空。A1询问IDsi 的部分私钥时，若E 中已有相应记录，则直接返回Dsi 。否则，A1执行H1 询问，返回(IDsi,Qsi,αi,ci) 。若ci=1 ，则B终止；否则，计算Dsi=αiPpu=αiaP ，返回Dsi 给A1，并将(IDsi,Dsi,Qsi) 添加到表E 。(7) 公钥询问Public-key-query: B保持列表
F=(IDsi,Xi,Psi) ，初始为空。当A1询问IDsi 的公钥时，若F 包含询问内容，返回Psi 给A1。否则，选择任意Xi∈Z∗q ,Psi=XiP ，返回Psi 给A1将(IDsi, Xi,Psi) 加入到F 表中。(8) 秘密值询问Secret-Value-query：当A1询问
IDsi 的秘密值时，如果ci=1 , B终止。否则，B查F 表，若F 表中有对应的IDsi ，则返回相应秘密值；否则B随机选择Xi∈Z∗q ，作为相应的秘密值，更新列表并返回Xi 。(9) 公钥替换询问Public-key-replace-query: A1对
IDsi 公钥替代询问时，A1随机选择一个公钥P′si 代替原公钥Psi 。设置Psi=P′si ,Xi=⊥ 。(10) 签密询问Signcryption-query：当A1对
(Mi,IDsi,L) 里的L={IDR1,IDR2,···,IDRn} 进行签密询问时，若IDsi≠ID∗ai ，则运行签密算法得到密文σ 。若IDsi=ID∗ai , B模拟算法生成一个签密。(a)B随机选择
ri∈Z∗q ,hi∈Z∗q 。(b)计算
Ri=riP−h−1iPsi 和Si=Dsi+hiriH4(Q) , B把σi=(Ri,Ci,Si) 给A1。e(Si,P)=e(Dsi+hiriH4(Q),P)=e(Dsi,P)e(hiriH4(Q),P)=e(αiaP,P)e(hiriH4(Q),P)=e(αiP,Ppu)e(hiriP,H4(Q))=e(Qsi,Ppu)e(hi(Ri+h−1iPsi),H4(Q))=e(Qsi,Ppu)e(hiRi+Psi,H4(Q)) (11) 输出Output：最后，A1输出一个元组
(M∗i,σ∗i,ID∗si,P∗si) 。如果ID∗si≠ID∗ai , B终止；否则，通过使用分叉引理，在用相同的随机带重放A1之后的两个不同的h′i , B在多项式时间内获得两个有效签名σ∗i=(M∗i,h∗i,ID∗si,R∗i,S∗i) 和\sigma^{*}'\!\!_i = (M^{*}'\!\!_i, h^{*}'\!\!_i,{\rm{ID}}_{{\rm{si}}}^{*}'\!\!_i,R^{*}'\!\!_i,S^{*}'\!\!_i) 。S∗i=D∗si+(X∗si+h∗ir∗i)H4(Q)=D∗si+(X∗i+h∗ir∗i)abP$ (1) \begin{aligned}S_i^* {\rm{'}} &= D_{{\rm{si}}}^* + (X_{{\rm{si}}}^* + h_i^{*}'r_i^*){H_4}(Q) \\& = D_{\rm si}^* + (X_i^* + h_i^{*}'r_i^*)abP\end{aligned} (2) 根据式(1)和式(2), B通过计算输出
abP 作为CDH实例的解决方案abP = (S_i^* - S_i^{*}')/(h_{_i}^*r_{_i}^* - h'_{_i}^{*}r_{_i}^*) 。引理 2 在随机预言模型下，假设一个敌手A2在t时间内能以不可忽略的优势
ε 攻破本文方案，则存在算法B，能以{\varepsilon '} \ge (\varepsilon - {q^s}/{2^k}){(1 - 1/({q^{{\rm{pk}}}} + m))^{{q_{{\rm{P}}k}} + m - 1 优势解决 CDH 问题的一个实例。证明 A2为攻击者，B为CDH问题的挑战者。B给定
(P,aP,bP) , B 的目标是使用A2解决 CDH问题，即计算abP 。(1) 系统建立Setup: B运行Setup算法，随机选择
s∈Z∗q 作为系统的主密钥，计算Ppu=sP 。B随机选取ID∗ai 作为挑战身份，B将params 和s 一起传递给A2。A2执行以下询问：(2) H1-query: B维持列表
L1=(IDsi,Qi,) ，初始为空。当A2对IDsi 进行询问时，B首先检测L1 表，若L1 存在(IDsi,Qi) , B就返回相应Qi ，否则：B随机选择Qi∈G1 ，更新列表，把Qi 发送给A2。(3) H2-query: B维持列表
L2=(ωi,βi,H2(ωi)) , B收到对ωi 的H2 询问时：(a)如果
H2(ωi) 存在L2 列表中，就把H2(ωi) 返回给A2。(b)否则，随机选择
βi∈Z∗q ，计算H2(ωi)=βiaP ，输出H2(ωi) ，添加(ωi,βi,H2(ωi)) 到列表L2 中。(4) H3-query: B维持
L3={Ci,Ri,Psi,IDsi,hi,γi} ，初始为空。当A2询问L3 时，B首先检测L3 ，若L3 存在，则返回hi ；否则B随机选择γi∈Z∗q ，令hi=γi ，增加元组到列表L3 中，并返回hi 给A2。(5) H4-query: A2对
H4(Ppu) 进行询问时，B令H4(Ppu)=aP ，并返回给A2。(6) 公钥询问Public-key-query: B保持列表
F=(IDsi,Xi,Psi) ，初始为空。当A2询问IDsi 公钥时，若F 列表中包含Psi ，则返回Psi 给A2。否则，随机选择Xi∈Z∗q 。若ci=0 ，计算Psi=XiP 。否则计算Psi=XibP 。返回Psi 给A2同时更新元组(IDsi,Xi, Psi) 到F 表中。(7) 签密询问Signcryption-query：当A2对
(Mi,IDsi,L) 这里的L={IDR1,IDR2,···,IDRn} 签密询问时，首先B查表。若ci=0 , B随机选择hi∈Z∗q ，计算Ri=−h−1iPsi ,Si=Dsi 。最后，B把σi=(Ri, Ci,Si,Ti) 给A2。e(Qsi,Ppu)e(hiRi+Psi,H4(Q))=e(Qsi,Ppu)=e(Qsi,s⋅P)=e(s⋅Qsi,P)=e(Dsi,P)=e(Si,P)\vspace30pt (8) 输出Output: A2输出一个元组
(M∗i,σ∗i,ID∗si, P∗si) 。如果ID∗si≠ID∗ai , B终止；否则，利用分叉引理，在用同样的任意带重放A2之后得到两个不一样h′i , B在多项式时间内获得两个有用签名σ∗i= (M∗i,h∗i,ID∗si,R∗i,S∗i) 和\sigma^{*}'\!\!_i \!=\!(M^{*}'\!\!_i,h^{*}'\!\!_i,{\rm{ID}}_{{\rm{si}}}^{*}'\!\!_i,R_i^{*}'\!\!_i,S_i^{*}'\!\!_i) 。S∗i=D∗si+(X∗si+h∗ir∗i)H4(Q)=D∗si+(X∗i+h∗ir∗i)abP (3) \begin{aligned}S_i^*{\rm{'}} & = D_{{\rm{si}}}^* + (X_{{\rm{si}}}^* + h^{*}'\!\!_i r_i^*){H_4}(Q) \\& = D_{{\rm{si}}}^* + (X_i^* + h^{*}'\!\!_i r_i^*)abP$\end{aligned} (4) 根据式(3)和式(4), B 通过计算输出abP 作为CDH实例的解决方案 abP=(S∗i−S∗′i)/(h∗ir∗i−h′∗ir∗i)。证毕4.2 聚合签密密文不可伪造性
定理2 假定CDH问题困难，本文异构聚合签密方案在随机预言模型下自适应选择消息攻击下不可伪造。
这个定理是通过结合引理3和引理4得到的。
引理 3 在随机预言模型下，假设敌手A1在时间t内能以不可忽略的优势
ε 攻破本文方案，则存在算法B，能以ε′≥(ε−qs/2k)(1−1/qpk)qPk 优势解决 CDH 问题的一个实例。证明 算法B首先设置在引理1中描述的公共参数。注意，在设置阶段，B设置
Ppu=aP 。然后，A1执行在引理1中描述的模拟询问。挑战者B以与引理1相同的方式回答A1的查询。(1)聚合解签密询问Aggregate De-signcryption query: A1向B提交一个密文集合
σ ，发送者的伪身份{IDsi}mi=1 ，接收者的身份集L∗={IDrj}nj=1 , B使用IBC-KG算法计算接收者的私钥{IDrj}nj=1 。如果它是一个有效的密文，A1首先检查σ 的有效性。之后，A1返回对密文σ 运行Aggregate de-signcrypt算法的结果。(2)输出Output: A1输出
{IDsi}mi=1 和{IDrj}nj=1 且对应的公钥{P∗si}mi=1 和{IDrj}nj=1 , m个消息{Mi}mi=1 和他们的聚合密文σ∗=(R∗i,C∗i,S∗i) 。伪造的聚合密文必须使用聚合解密来验证，即e(S∗,P)=e(m∑i=1Q∗si,Ppu)⋅e(m∑i=1(D∗si+hi⋅riH4(Ppu)),Ppu)=e(m∑i=1Q∗si,Ppu)⋅e(m∑i=1(P∗si,+hi⋅Ri),H4(Ppu)) Ppu=aP,H4(Ppu)=tP,Q∗si=αibP 利用分叉引理我们得到
\quadabP=(S∗−tm∑i=1XiP+ h∗iR∗i)(m∑i=1αi)−1 引理 4 在随机预言模型下，假设敌手A2在时间t内能以不可忽略的优势
ε 攻破本文方案，则存在算法B，能以ε′≥(ε−qs/2k)(1−1/(qpk+m))qPk+m−1 优势解决CDH问题的一个实例。证明 B设置与引理2中描述的公共参数。挑战者B以与引理2相同的方式回答A2的查询。
输出Output: A2输出
{IDsi}mi=1 和{IDrj}nj=1 且对应的公钥{P∗si}mi=1 和{Q∗rj}nj=1 , m个消息{Mi}mi=1 和它们的聚合密文σ∗=(R∗i,C∗i,S∗i) 。伪造的聚合密文必须使用聚合解密来验证。利用分叉引理我们得到
abP=(S∗−tm∑i=1XiP+h∗iR∗i)(m∑i=1αi)−1 证毕5. 性能分析
将本文方案和Niu方案进行效率对比。用
Tadd 代表点加运算耗费的时间，Tpm 代表点乘运算耗费的时间，Tp 代表双线性对运算耗费的时间，TH 代表Hash函数映射到点耗费的时间，Th 代表一次普通Hash函数耗费的时间。|m| 代表消息的长度，|U| 代表用户身份的长度，|G1| 代表G1 群中元素长度。本文方案使用的基本运算耗费的时间如表1所示。实验环境为戴尔笔记本(I7-4700 CPU @3.20 GHz, 16 GB内存和Ubuntu Linux操作系统)。同时使用了密码函数库(Pairing-Based Cryptography, PBC)。
表 1 基本运算耗费的时间(ms)Tadd Tpm Tp TH Th 0.023 3.382 3.711 6.720 1.024 表2分析了两个方案的签密以及解签密效率。从表2可以看出，在签密阶段，本文方案效率略低于Niu[16]方案，是因为比Niu方案多了一个Hash函数，但是安全性因此略有提高。在解签密阶段，本文方案与Niu方案效率相当。
表 2 签密方案效率比较方案 签密 解签密 安全性 Niu方案 (2n+5)Tpm+Tp+2TH+Th +(n+3)Tadd≥41.849 nTpm+5Tp+3TH+Th +(n+1)Tadd≥42.143 低 本文方案 (2n+5)Tpm+Tp+3TH+Th +(n+3)Tadd≥48.569 nTpm+5Tp+3TH+Th +(n+1)Tadd≥42.143 高 以上性能分析表明，新方案在运算效率上与Niu方案相当，这是因为本文的主要工作是提高原方案的安全性，确保方案可以抵抗不可伪造性攻击。
6. 结束语
具有系统隐私保护功能的异构聚合签密方案不仅解决了不同密码系统之间多个签密密文验证困难的问题，同时还具有双重隐私保护功能。本文分析了Niu方案的安全性。指出了该方案存在KGC伪造攻击，并分析了产生KGC被动攻击的原因，描述了KGC伪造攻击的过程。随后对Niu方案进行了改造，给出了新的方案。证明了本文方案满足不可伪造性。本文方案具有较高安全性，未来会进一步地研究降低运算效率。
-
表 1 4种常用等效电路模型
等效电路模型 器件组成 模型特性方程 等效电路 参数辨识复杂程度 特点 Rint模型 Uv, R0 Ut=Uv–IR0 
简单 模型简单；精度差；无法模拟
电池动态特性Thevenin模型 Uv,R0, R1,C1 U1=IR1·[1–e–t/τ1]
Ut=Uv–IR0–U1
复杂 考虑了电池极化的影响 2阶电阻电容
并联等效模型Uv,R0,R1, C1,R2,C2 U1=IR1·[1–e–t/τ1]
U2=IR2·[1–e–t/τ2]
Ut=Uv–IR0–U1–U2
非常复杂 考虑了电池极化的影响；
模型精度高PNGV模型 Uv, R0, R1, C1, C3 U1=IR1·[1–e–t/τ1]
U3=I/C3
Ut=Uv–IR0–U1–U3
非常复杂 考虑负载电流对OCV的影响 
下载: 导出CSV
表 2 各类SoC估计方法的主要优点和缺点
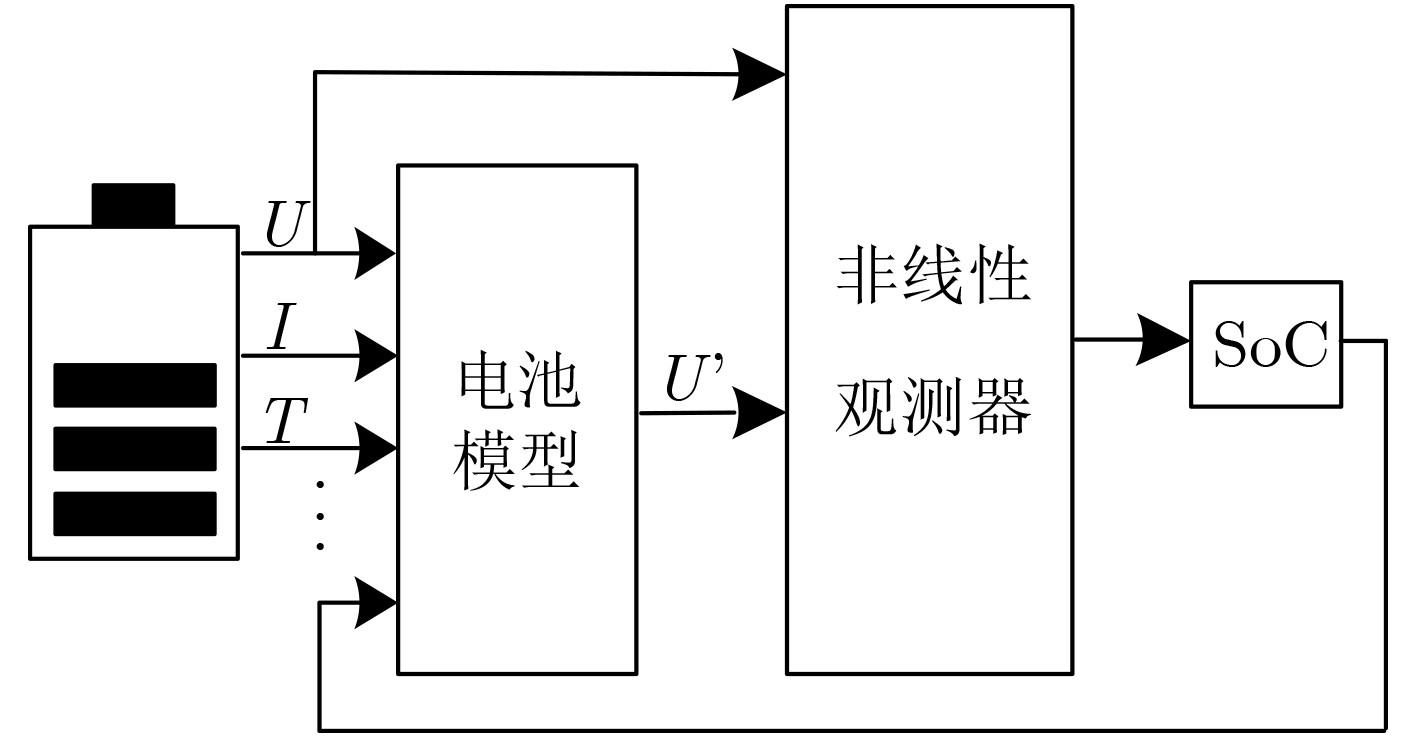
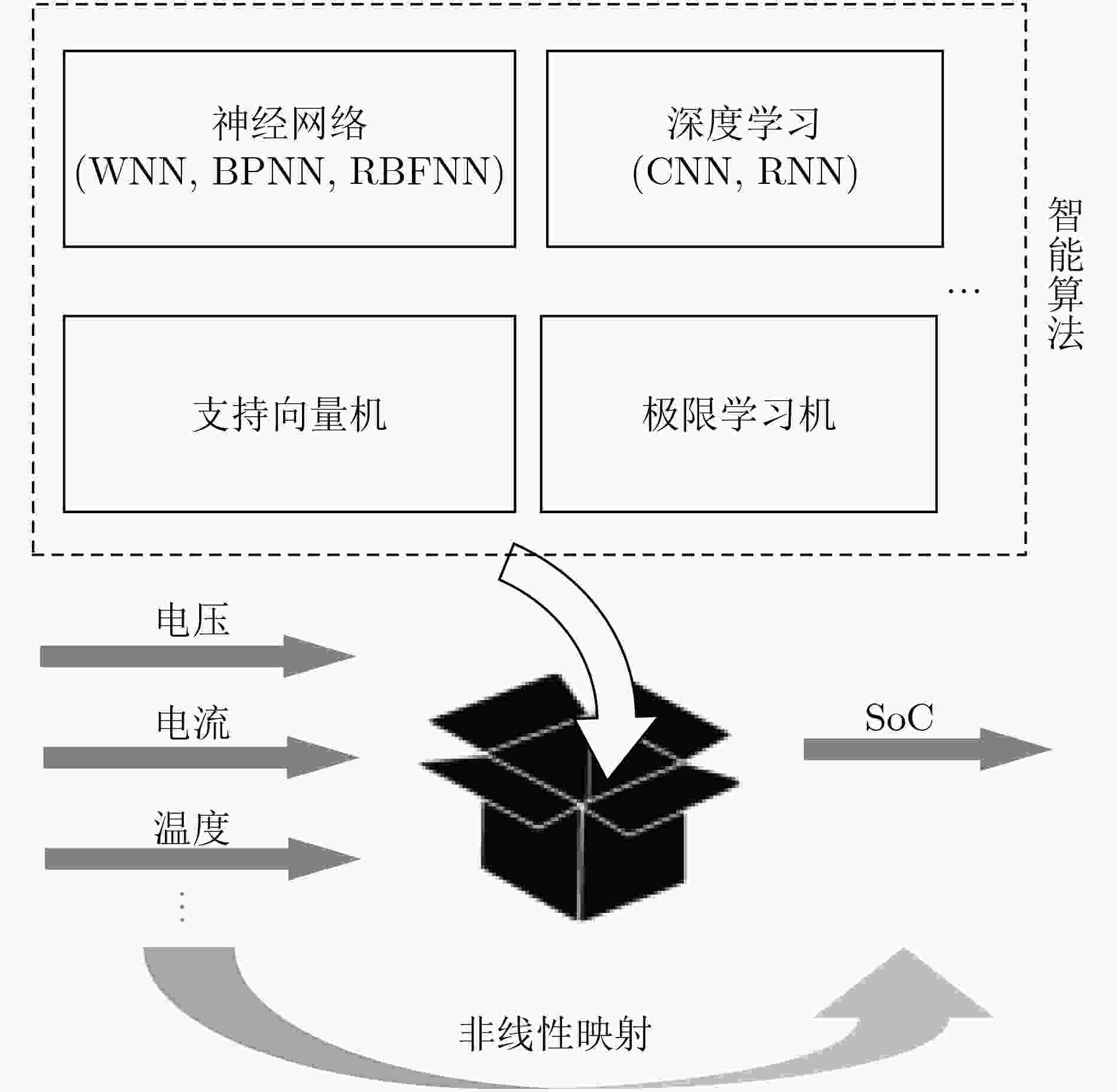
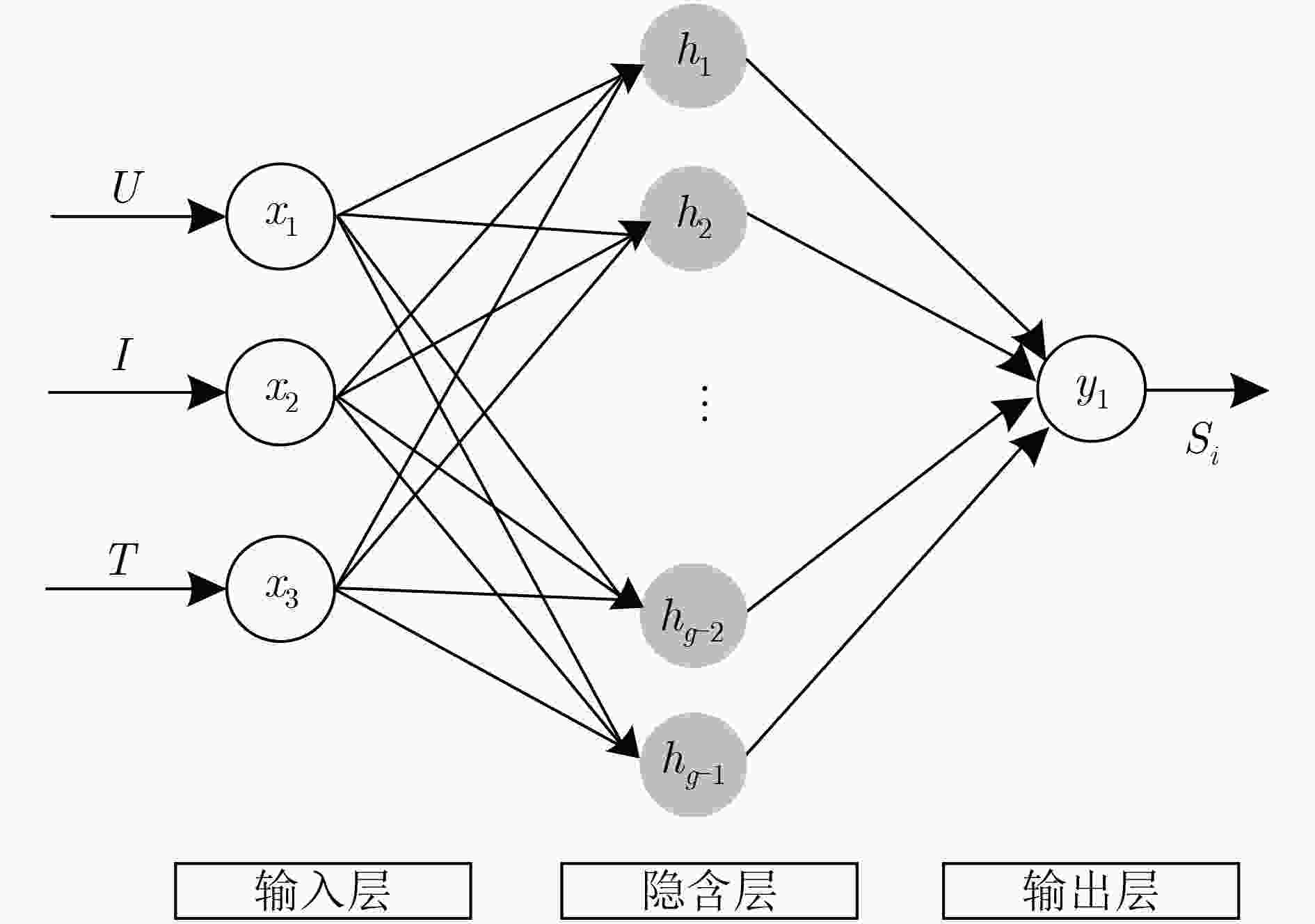
估算方法 优点 缺点 查表法 准确、可靠、原理简单 耗时长、能源浪费、不能实时估计 安时积分法 估算速度快、易实现 开环估计方法，存在累计误差 基于模型的估算方法 闭环估计，不需要精确的SoC初始值、估算误差小 建模困难、参数辨识难度大、计算量大 基于数据方法 不需要对电池建模、可以自学习网络参数、计算量小 对数据要求高、离线训练耗时长 混合方法 估算精度高、有很好的泛化性和鲁棒性 计算复杂、能耗大、估算速度慢
下载: 导出CSV
-
[1] CHEN Lin, WANG Zhengzheng, LV Zhiqiang, et al. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algorithms[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8797–8807. doi: 10.1109/TPEL.2017.2782721 [2] TIAN Yong, LAI Rucong, LI Xiaoyu, et al. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter[J]. Applied Energy, 2020, 265: 114789. doi: 10.1016/j.apenergy.2020.114789 [3] JIN Long, LI Shuai, and HU Bin. RNN models for dynamic matrix inversion: A control-theoretical perspective[J]. IEEE Transactions on Industrial Informatics, 2018, 14(1): 189–199. doi: 10.1109/TII.2017.2717079 [4] XIONG Rui, CAO Jiayi, YU Quanqing, et al. Critical review on the battery state of charge estimation methods for electric vehicles[J]. IEEE Access, 2018, 6: 1832–1843. doi: 10.1109/ACCESS.2017.2780258 [5] ALI M U, ZAFAR A N, NENGROO S H, et al. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation[J]. Energies, 2019, 12(3): 446. doi: 10.3390/en12030446 [6] SHEN Ping, OUYANG Minggao, HAN Xuebing, et al. Error analysis of the model-based state-of-charge observer for lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8055–8064. doi: 10.1109/TVT.2018.2842820 [7] MOUSSALLI Z, SEDRA M B, and LAACHIR A A. State of charge estimation algorithms in lithium-ion battery-powered electric vehicles[C]. 2018 International Conference on Electronics, Control, Optimization and Computer Science, Kenitra, Morocco, 2018: 1–6. [8] JULIEN C, MAUGER A, VIJH A, et al. Lithium Batteries: Science and Technology[M]. Switzerland: Springer, 2016: 29–34. [9] YONG Jiaying, RAMACHANDARAMURTHY V K, TAN Kangmiao, et al. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects[J]. Renewable and Sustainable Energy Reviews, 2015, 49: 365–385. doi: 10.1016/j.rser.2015.04.130 [10] PATTIPATI B, SANKAVARAM C, and PATTIPATI K. System identification and estimation framework for pivotal automotive battery management system characteristics[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) , 2011, 41(6): 869–884. doi: 10.1109/TSMCC.2010.2089979 [11] LI Jianhua and LIU Mingsheng. State-of-charge estimation of batteries based on open-circuit voltage and time series neural network[C]. The 2019 6th International Conference on Systems and Informatics, Shanghai, China, 2019. doi: 10.1109/ICSAI48974.2019.9010535. [12] WU S L, CHEN H C, TSAI M Y, et al. AC impedance based online state-of-charge estimation for li-ion battery[C]. 2017 International Conference on Information, Communication and Engineering, Xiamen, China, 2017: 53–56. doi: 10.1109/ICICE.2017.8479183. [13] SHEN Ping, OUYANG Minggao, LU Languang, et al. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 92–103. doi: 10.1109/TVT.2017.2751613 [14] BARAI A, WIDANAGE W D, MARCO J, et al. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells[J]. Journal of Power Sources, 2015, 295: 99–107. doi: 10.1016/j.jpowsour.2015.06.140 [15] YANG Fangfang, SONG Xiangbao, XU Fan, et al. State-of-charge estimation of lithium-ion batteries via long short-term memory network[J]. IEEE Access, 2019, 7: 53792–53799. doi: 10.1109/ACCESS.2019.2912803 [16] TRUCHOT C, DUBARRY M, and LIAW B Y. State-of-charge estimation and uncertainty for lithium-ion battery strings[J]. Applied Energy, 2014, 119: 218–227. doi: 10.1016/j.apenergy.2013.12.046 [17] LASHWAY C R and MOHAMMED O A. Adaptive battery management and parameter estimation through physics-based modeling and experimental verification[J]. IEEE Transactions on Transportation Electrification, 2016, 2(4): 454–464. doi: 10.1109/TTE.2016.2558843 [18] NG K S, MOO C S, CHEN Y P, et al. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506–1511. doi: 10.1016/j.apenergy.2008.11.021 [19] ZHENG Yuejiu, OUYANG Minggao, HAN Xuebing, et al. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles[J]. Journal of Power Sources, 2018, 377: 161–188. doi: 10.1016/j.jpowsour.2017.11.094 [20] FULLER T F, DOYLE M, and NEWMAN J. Simulation and optimization of the dual lithium ion insertion cell[J]. Journal of the Electrochemical Society, 1994, 141(1): 1–10. doi: 10.1149/1.2054684 [21] LOTFI N, LANDERS R G, LI Jie, et al. Reduced-order electrochemical model-based SOC observer with output model uncertainty estimation[J]. IEEE Transactions on Control Systems Technology, 2017, 25(4): 1217–1230. doi: 10.1109/TCST.2016.2598764 [22] LIU Guangming, LU Languang, FU Hong, et al. A comparative study of equivalent circuit models and enhanced equivalent circuit models of lithium-ion batteries with different model structures[C]. 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific, Beijing, China, 2014: 1–6. doi: 10.1109/ITEC-AP.2014.6940946. [23] LUO Yifeng, GONG C S A, CHANG Longxi, et al. AC impedance technique for dynamic and static state of charge analysis for Li-ion battery[C]. 2013 IEEE International Symposium on Consumer Electronics, Hsinchu, China, 2013: 9–10. doi: 10.1109/ISCE.2013.6570268. [24] EDDAHECH A, BRIAT O, BERTRAND N, et al. Behavior and state-of-health monitoring of Li-ion batteries using impedance spectroscopy and recurrent neural networks[J]. International Journal of Electrical Power & Energy Systems, 2012, 42(1): 487–494. doi: 10.1016/j.ijepes.2012.04.050 [25] Wang Qiankun, HE Yijun, SHEN Jiani, et al. State of charge-dependent polynomial equivalent circuit modeling for electrochemical impedance spectroscopy of lithium-ion batteries[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8449–8460. doi: 10.1109/TPEL.2017.2780184 [26] HE Hongwen, XIONG Rui, GUO Hongqiang, et al. Comparison study on the battery models used for the energy management of batteries in electric vehicles[J]. Energy Conversion and Management, 2012, 64: 113–121. doi: 10.1016/j.enconman.2012.04.014 [27] LAI Xin, ZHENG Yuejiu, and SUN Tao. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries[J]. Electrochimica Acta, 2018, 259: 566–577. doi: 10.1016/j.electacta.2017.10.153 [28] NEMES R, CIORNEI S, RUBA M, et al. Modeling and simulation of first-order Li-Ion battery cell with experimental validation[C]. The 2019 8th International Conference on Modern Power Systems, Cluj Napoca, Romania, 2019. doi: 10.1109/MPS.2019.8759769. [29] HE Hongwen, XIONG Rui, ZHANG Xiaowei, et al. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved thevenin model[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1461–1469. doi: 10.1109/TVT.2011.2132812 [30] ZHANG Xi, LU Jinling, YUAN Shifei, et al. A novel method for identification of lithium-ion battery equivalent circuit model parameters considering electrochemical properties[J]. Journal of Power Sources, 2017, 345: 21–29. doi: 10.1016/j.jpowsour.2017.01.126 [31] HE Hongwen, XIONG Rui, and FAN Jinxin. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach[J]. Energies, 2011, 4(4): 582–598. doi: 10.3390/en4040582 [32] LIU Xiangyong, LI Wanli, and ZHOU Aiguo. PNGV equivalent circuit model and SOC estimation algorithm for lithium battery pack adopted in AGV vehicle[J]. IEEE Access, 2018, 6: 23639–23647. doi: 10.1109/ACCESS.2018.2812421 [33] ZOU Changfu, HU Xiaosong, DEY S, et al. Nonlinear fractional-order estimator with guaranteed robustness and stability for lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5951–5961. doi: 10.1109/TIE.2017.2782691 [34] YU Quanqing, XIONG Rui, and LIN Cheng. Online estimation of state-of-charge based on the H infinity and unscented Kalman filters for lithium ion batteries[J]. Energy Procedia, 2017, 105: 2791–2796. doi: 10.1016/j.egypro.2017.03.600 [35] NEJAD S, GLADWIN D T, and STONE D A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states[J]. Journal of Power Sources, 2016, 316: 183–196. doi: 10.1016/j.jpowsour.2016.03.042 [36] HE Hongwen, XIONG Rui, and PENG Jiankun. Real-time estimation of battery state-of-charge with unscented Kalman filter and RTOS μCOS-II platform[J]. Applied Energy, 2016, 162: 1410–1418. doi: 10.1016/j.apenergy.2015.01.120 [37] PAN Haihong, LV Zhiqiang, LIN Weilong, et al. State of charge estimation of lithium-ion batteries using a grey extended Kalman filter and a novel open-circuit voltage model[J]. Energy, 2017, 138: 764–775. doi: 10.1016/j.energy.2017.07.099 [38] DONG Guangzhong, WEI Jingwen, and CHEN Zonghai. Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries[J]. Journal of Power Sources, 2016, 328: 615–626. doi: 10.1016/j.jpowsour.2016.08.065 [39] WANG Yujie, ZHANG Chenbin, and CHEN Zonghai. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter[J]. Journal of Power Sources, 2015, 279: 306–311. doi: 10.1016/j.jpowsour.2015.01.005 [40] BARTLETT A, MARCICKI J, ONORI S, et al. Electrochemical model-based state of charge and capacity estimation for a composite electrode lithium-ion battery[J]. IEEE Transactions on Control Systems Technology, 2016, 24(2): 384–399. doi: 10.1109/TCST.2015.2446947 [41] AUNG H and LOW K S. Temperature dependent state-of-charge estimation of lithium ion battery using dual spherical unscented Kalman filter[J]. IET Power Electronics, 2015, 8(10): 2026–2033. doi: 10.1049/iet-pel.2014.0863 [42] AUNG H, LOW K S, and GOH S T. State-of-charge estimation of lithium-ion battery using square root spherical unscented Kalman filter (Sqrt-UKFST) in nanosatellite[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 4774–4783. doi: 10.1109/TPEL.2014.2361755 [43] ZHU Qiao, LI Liang, HU Xiaosong, et al. H∞-based nonlinear observer design for state of charge estimation of lithium-ion battery with polynomial parameters[J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10853–10865. doi: 10.1109/TVT.2017.2723522 [44] LIU Congzhi, ZHU Qiao, LI Liang, et al. A state of charge estimation method based on H∞ observer for switched systems of lithium-ion nickel–manganese–cobalt batteries[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8128–8137. doi: 10.1109/TIE.2017.2701766 [45] TANG Xiaopeng, WANG Yujie, and CHEN Zonghai. A method for state-of-charge estimation of LiFePO4 batteries based on a dual-circuit state observer[J]. Journal of Power Sources, 2015, 296: 23–29. doi: 10.1016/j.jpowsour.2015.07.028 [46] XU Jun, MI C C, CAO Binggang, et al. The state of charge estimation of lithium-ion batteries based on a proportional-integral observer[J]. IEEE Transactions on Vehicular Technology, 2014, 63(4): 1614–1621. doi: 10.1109/TVT.2013.2287375 [47] XIONG Binyu, ZHAO Jiyun, SU Yixin, et al. State of charge estimation of vanadium redox flow battery based on sliding mode observer and dynamic model including capacity fading factor[J]. IEEE Transactions on Sustainable Energy, 2017, 8(4): 1658–1667. doi: 10.1109/TSTE.2017.2699288 [48] CHEN Xiaopeng, SHEN Weixiang, DAI Mingxiang, et al. Robust adaptive sliding-mode observer using RBF neural network for lithium-ion battery state of charge estimation in electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 1936–1947. doi: 10.1109/TVT.2015.2427659 [49] WANG Baojin, LIU Zhiyuan, LI S E, et al. State-of-charge estimation for lithium-ion batteries based on a nonlinear fractional model[J]. IEEE Transactions on Control Systems Technology, 2017, 25(1): 3–11. doi: 10.1109/TCST.2016.2557221 [50] HU Xiaosong, SUN Fengchun, and ZOU Yuan. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive luenberger observer[J]. Energies, 2010, 3(9): 1586–1603. doi: 10.3390/en3091586 [51] XING Yinjiao, HE Wei, PECHT M, et al. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113: 106–115. doi: 10.1016/j.apenergy.2013.07.008 [52] YANG Fangfang, XING Yinjiao, WANG Dong, et al. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile[J]. Applied Energy, 2016, 164: 387–399. doi: 10.1016/j.apenergy.2015.11.072 [53] PARK J, KIM G, NA W, et al. Nonlinear observer and simplified equivalent circuit model-based EKF-SoC estimator of a rechargeable LiFePo4 cell[C]. The 2019 10th International Conference on Power Electronics and ECCE Asia, Busan, Korea (South), 2019. [54] YAN Wuzhao, ZHANG Bin, ZHAO Guangquan, et al. A battery management system with a lebesgue-sampling-based extended kalman filter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 3227–3236. doi: 10.1109/tie.2018.2842782 [55] HE Hongwen, QIN Hongzhou, SUN Xiaokun, et al. Comparison study on the battery SOC estimation with EKF and UKF algorithms[J]. Energies, 2013, 6(10): 5088–5100. doi: 10.3390/en6105088 [56] WANG Weida, WANG Xiantao, XIANG Changle, et al. Unscented kalman filter-based battery SOC estimation and peak power prediction method for power distribution of hybrid electric vehicles[J]. IEEE Access, 2018, 6: 35957–35965. doi: 10.1109/ACCESS.2018.2850743 [57] EI DIN M S, HUSSEIN A A, and ABDEL-HAFEZ M F. Improved battery SOC estimation accuracy using a modified UKF with an adaptive cell model under real EV operating conditions[J]. IEEE Transactions on Transportation Electrification, 2018, 4(2): 408–417. doi: 10.1109/TTE.2018.2802043 [58] PENG Simin, CHEN Chong, SHI Hongbing, et al. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator[J]. IEEE Access, 2017, 5: 13202–13212. doi: 10.1109/ACCESS.2017.2725301 [59] HE Cheng, LIU Changchun, WU Yang, et al. Estimation for SOC of electric vehical lithium battery based on artificial immune particle filter[C]. The 2018 3rd International Conference on Smart City and Systems Engineering, Xiamen, China, 2018: 675–678. doi: 10.1109/ICSCSE.2018.00145. [60] ZHANG Kai, MA Jian, ZHAO Xuan, et al. State of charge estimation for lithium battery based on adaptively weighting cubature particle filter[J]. IEEE Access, 2019, 7: 166657–166666. doi: 10.1109/access.2019.2953478 [61] HE Yao, LIU Xingtao, ZHANG Chenbin, et al. A new model for State-of-Charge (SOC) estimation for high-power Li-ion batteries[J]. Applied Energy, 2013, 101: 808–814. doi: 10.1016/j.apenergy.2012.08.031 [62] SHEN Yanqing. Hybrid unscented particle filter based state-of-charge determination for lead-acid batteries[J]. Energy, 2014, 74: 795–803. doi: 10.1016/j.energy.2014.07.051 [63] ELSAYED A and GRIMBLE M J. A new approach to H∞ design of optimal digital linear filters[J]. IMA Journal of Mathematical Control and Information, 1989, 6(2): 233–251. doi: 10.1093/imamci/6.2.233 [64] ZHANG Fei, LIU Guangjun, FANG Lijin, et al. Estimation of battery state of charge with H∞ observer: Applied to a robot for inspecting power transmission lines[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1086–1095. doi: 10.1109/TIE.2011.2159691 [65] CHEN Ning, ZHANG Peng, DAI Jiayang, et al. Estimating the state-of-charge of lithium-ion battery using an h-infinity observer based on electrochemical impedance model[J]. IEEE Access, 2020, 8: 26872–26884. doi: 10.1109/ACCESS.2020.2971002 [66] CACCIATO M, NOBILE G, SCARCELLA G, et al. Real-time model-based estimation of SOC and SOH for energy storage systems[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 794–803. doi: 10.1109/TPEL.2016.2535321 [67] WEI Zhongbao, MENG Shujuan, XIONG Binyu, et al. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer[J]. Applied Energy, 2016, 181: 332–341. doi: 10.1016/j.apenergy.2016.08.103 [68] ZHONG Qishui, ZHONG Fuli, CHENG Jun, et al. State of charge estimation of lithium-ion batteries using fractional order sliding mode observer[J]. ISA Transactions, 2017, 66: 448–459. doi: 10.1016/j.isatra.2016.09.017 [69] DAI Kangwei, WANG Ju, and HE Hongwen. An improved SOC estimator using time-varying discrete sliding mode observer[J]. IEEE Access, 2019, 7: 115463–115472. doi: 10.1109/ACCESS.2019.2932507 [70] HOSSAIN LIPU M S, HANNAN M A, HUSSAIN A, et al. Extreme learning machine model for state-of-charge estimation of lithium-ion battery using gravitational search algorithm[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 4225–4234. doi: 10.1109/TIA.2019.2902532 [71] HU Xiaosong, LI S E, and YANG Yalian. Advanced machine learning approach for lithium-ion battery state estimation in electric vehicles[J]. IEEE Transactions on Transportation Electrification, 2016, 2(2): 140–149. doi: 10.1109/TTE.2015.2512237 [72] 董哲康, 杜晨杰, 林辉品, 等. 基于多通道忆阻脉冲耦合神经网络的多帧图像超分辨率重建算法[J]. 电子与信息学报, 2020, 42(4): 835–843. doi: 10.11999/JEIT190868DONG Zhekang, DU Chenjie, LIN Huipin, et al. Multi-channel memristive pulse coupled neural network based multi-frame images super-resolution reconstruction algorithm[J]. Journal of Electronics &Information Technology, 2020, 42(4): 835–843. doi: 10.11999/JEIT190868 [73] ÁLVAREZ ANTÓN J C, GARCÍA NIETO P J, BLANCO VIEJO C, et al. Support vector machines used to estimate the battery state of charge[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5919–5926. doi: 10.1109/TPEL.2013.2243918 [74] 刘彬, 杨有恒, 赵志彪, 等. 一种基于正则优化的批次继承极限学习机算法[J]. 电子与信息学报, 2020, 42(7): 1734–1742. doi: 10.11999/JEIT190502LIU Bin, YANG Youheng, ZHAO Zhibiao, et al. A batch inheritance extreme learning machine algorithm based on regular optimization[J]. Journal of Electronics &Information Technology, 2020, 42(7): 1734–1742. doi: 10.11999/JEIT190502 [75] EDDAHECH A, BRIAT O, and VINASSA J M. Adaptive voltage estimation for EV Li-ion cell based on artificial neural networks state-of-charge meter[C]. 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 2012: 1318–1324. doi: 10.1109/ISIE.2012.6237281. [76] ZHOU Fengwu, WANG Lujun, LIN Huiping, et al. High accuracy state-of-charge online estimation of EV/HEV lithium batteries based on adaptive wavelet neural network[C]. 2013 ECCE Asia Downunder, Melbourne, Australia, 2013: 513–517. doi: 10.1109/ECCE-Asia.2013.6579145. [77] GAO L, SONG Y, and DOUGAL R A. Wavelet neural network based battery state-of-charge estimation for portable electronics applications[C]. The 20th Annual IEEE Applied Power Electronics Conference and Exposition, Austin, USA, 2005: 998–1002. doi: 10.1109/APEC.2005.1453111. [78] TONG Shijie, LACAP J H, and PARK J W. Battery state of charge estimation using a load-classifying neural network[J]. Journal of Energy Storage, 2016, 7: 236–243. doi: 10.1016/j.est.2016.07.002 [79] KANG Liuwang, ZHAO Xuan, and MA Jian. A new neural network model for the state-of-charge estimation in the battery degradation process[J]. Applied Energy, 2014, 121: 20–27. doi: 10.1016/j.apenergy.2014.01.066 [80] CUI Deyu, XIA Bizhong, ZHANG Ruifeng, et al. A novel intelligent method for the state of charge estimation of lithium-ion batteries using a discrete wavelet transform-based wavelet neural network[J]. Energies, 2018, 11(4): 995. doi: 10.3390/en11040995 [81] LIPU M S H, HANNAN M A, HUSSAIN A, et al. Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection[J]. Journal of Renewable and Sustainable Energy, 2017, 9(6): 064102. doi: 10.1063/1.5008491 [82] LIU Yanwei, ZHAO Kegang, HUANG Xiangdong, et al. A new method based on RBFNN in SOC estimation of HEV battery[C]. The 29th Chinese Control Conference, Beijing, China, 2010: 4923–4927. [83] ABBAS G, NAWAZ M, and KAMRAN F. Performance comparison of NARX & RNN-LSTM neural networks for LiFePO4 battery state of charge estimation[C]. The 2019 16th International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 2019: 463–468. [84] YANG Fangfang, LI Weihua, LI Chuan, et al. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network[J]. Energy, 2019, 175: 66–75. doi: 10.1016/j.energy.2019.03.059 [85] HASTIE T, TIBSHIRANI R, and FRIEDMAN J. The Elements of Statistical Learning[M]. New York: Springer, 2009: 745. [86] SCHÖLKOPF B and SMOLA A J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond[M]. Cambridge: MIT Press, 2001: 187–188. [87] LI Ran, XU Shihui, LI Sibo, et al. State of charge prediction algorithm of lithium-ion battery based on PSO-SVR cross validation[J]. IEEE Access, 2020, 8: 10234–10242. doi: 10.1109/ACCESS.2020.2964852 [88] ZHANG Li, LI Kang, DU Dajun, et al. A sparse least squares support vector machine used for SOC estimation of Li-ion Batteries[J]. IFAC-PapersOnLine, 2019, 52(11): 256–261. doi: 10.1016/j.ifacol.2019.09.150 [89] HUANG Guangbin, ZHU Qinyu, and SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. doi: 10.1016/j.neucom.2005.12.126 [90] DU Jiani, LIU Zhitao, and WANG Youyi. State of charge estimation for Li-ion battery based on model from extreme learning machine[J]. Control Engineering Practice, 2014, 26: 11–19. doi: 10.1016/j.conengprac.2013.12.014 [91] LIU Shiqi, WANG Junhua, LIU Qisheng, et al. Deep-discharging li-ion battery state of charge estimation using a partial adaptive forgetting factors least square method[J]. IEEE Access, 2019, 7: 47339–47352. doi: 10.1109/ACCESS.2019.2909274 [92] MENG Jinhao, STROE D I, RICCO M, et al. A simplified model-based state-of-charge estimation approach for lithium-ion battery with dynamic linear model[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7717–7727. doi: 10.1109/TIE.2018.2880668 [93] SHEN Yanqing. A combined state space model with adaptive neural compensator based state of charge determination method for lithium-ion batteries[J]. Electrochimica Acta, 2020, 336: 135664. doi: 10.1016/j.electacta.2020.135664 [94] OUYANG Quan, CHEN Jian, and ZHENG Jian. State-of-charge observer design for batteries with online model parameter identification: A robust approach[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5820–5831. doi: 10.1109/TPEL.2019.2948253 [95] AWADALLAH M A and VENKATESH B. Accuracy improvement of SOC estimation in lithium-ion batteries[J]. Journal of Energy Storage, 2016, 6: 95–104. doi: 10.1016/j.est.2016.03.003 [96] ZAHID T, XU Kun, LI Weimin, et al. State of charge estimation for electric vehicle power battery using advanced machine learning algorithm under diversified drive cycles[J]. Energy, 2018, 162: 871–882. doi: 10.1016/j.energy.2018.08.071 [97] SHEN W X, CHAN C C, LO E W, et al. Adaptive neuro-fuzzy modeling of battery residual capacity for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2002, 49(3): 677–684. doi: 10.1109/TIE.2002.1005395 期刊类型引用(2)
1. 冀会芳，刘连东，黄严严，程庆丰. 一类PKI-IBC的双向匿名异构签密方案. 电信科学. 2020(04): 91-98 . 
百度学术2. 张玉磊，刘祥震，郎晓丽，张永洁，王彩芬. 一种异构混合群组签密方案的安全性分析与改进. 电子与信息学报. 2019(11): 2708-2714 . 
本站查看其他类型引用(4)
-
下载:
百度学术
计量
- 文章访问数: 3551
- HTML全文浏览量: 1701
- PDF下载量: 437
- 被引次数: 6
下载:
