A Decoupling and Dimension Dividing Multi-parameter Estimation Method for Cross-band SAR Scattering Centers
-
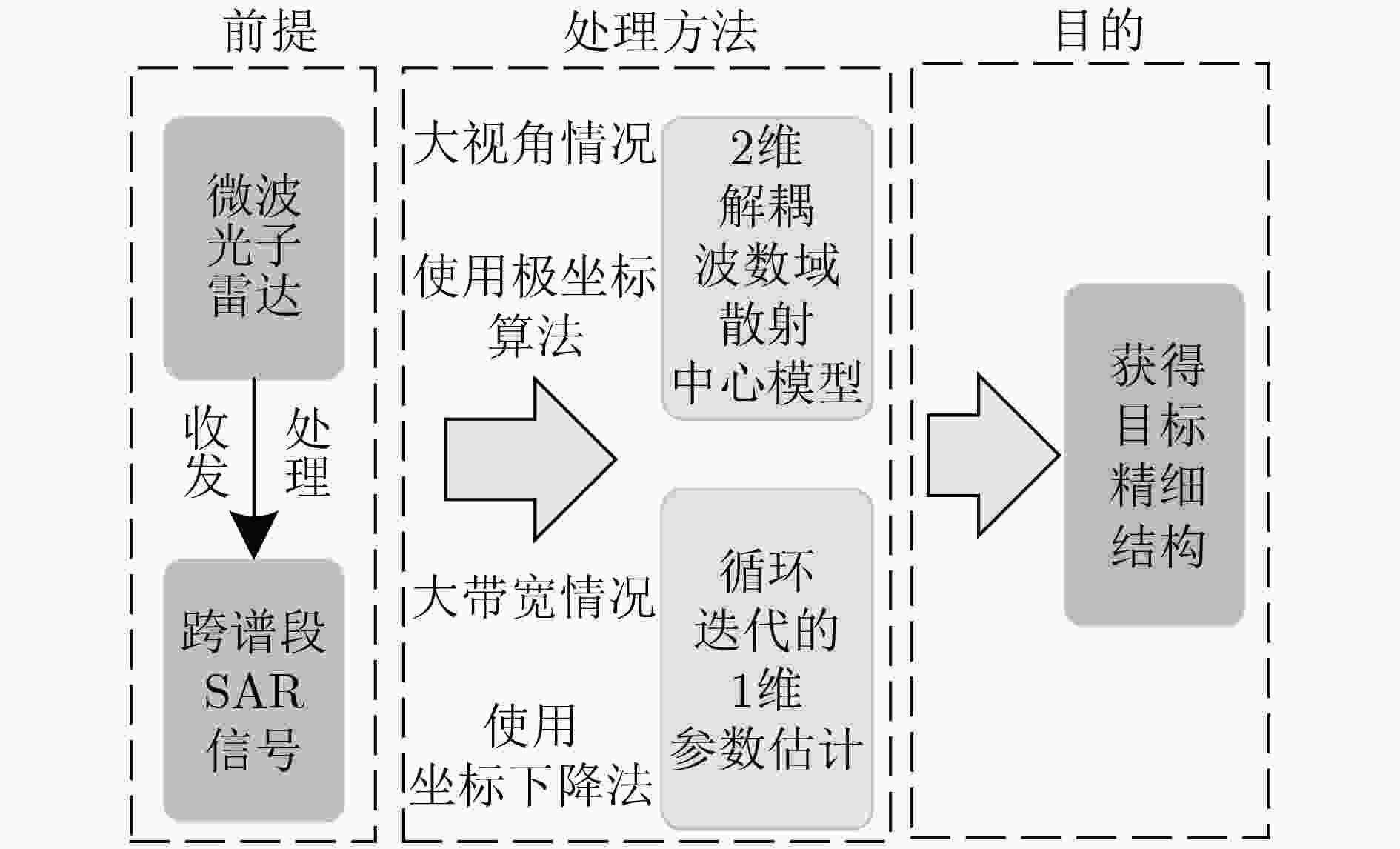
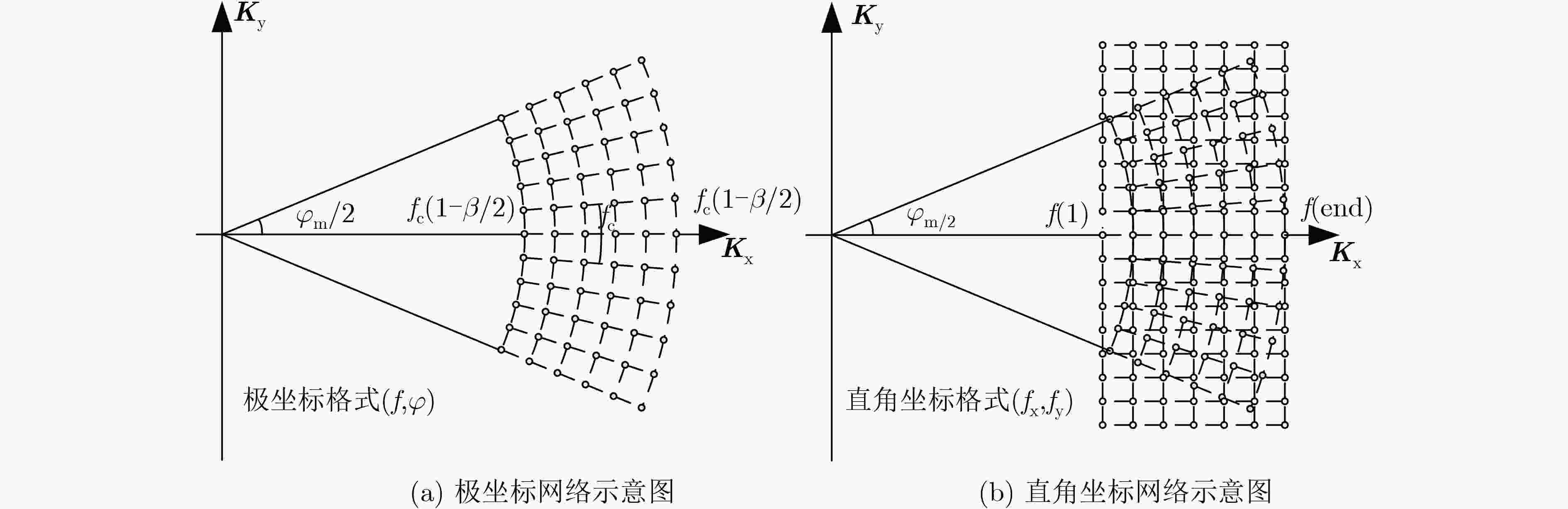
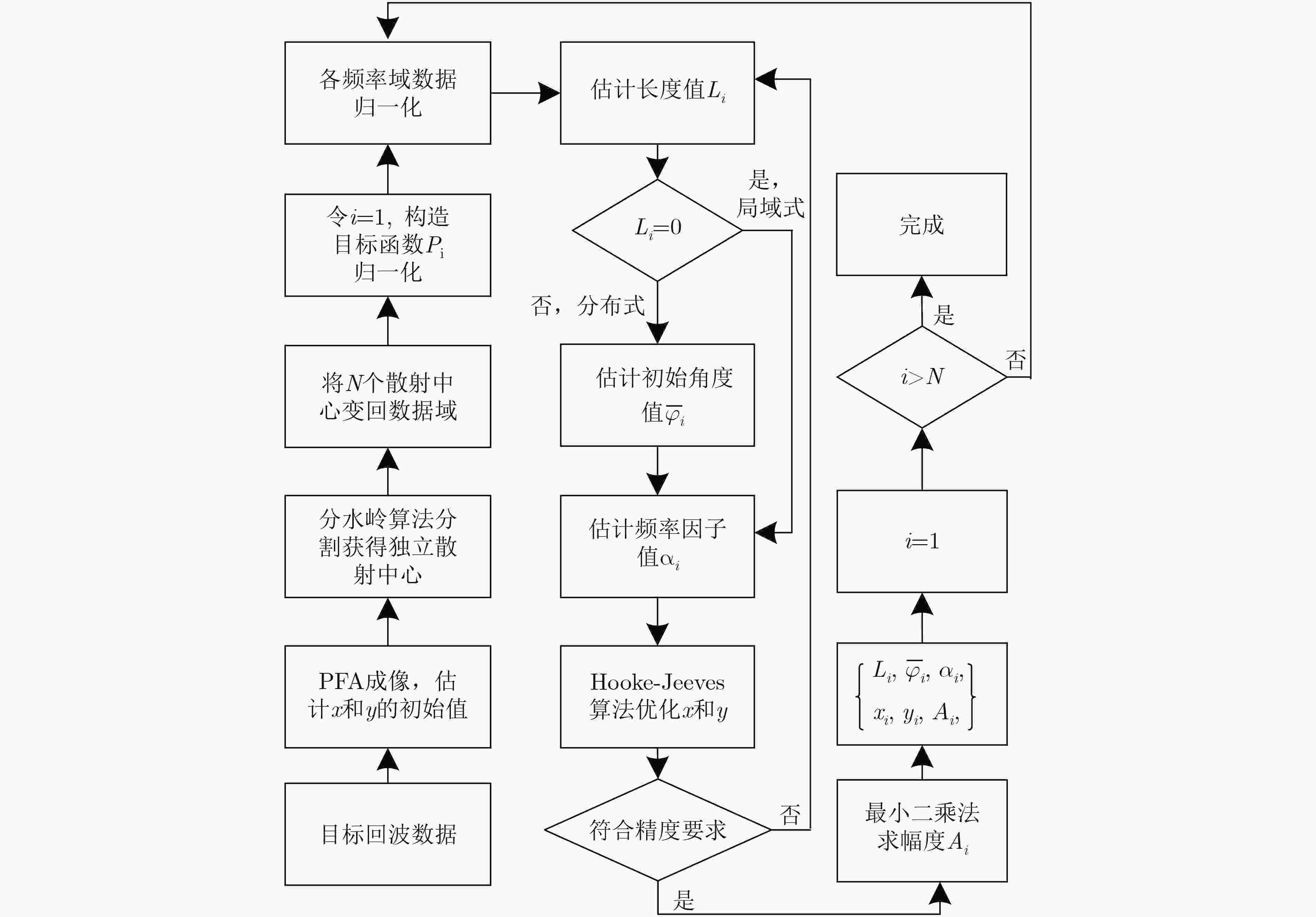
摘要: 微波光子雷达发射大带宽跨谱段的信号,为目标的精细电磁特性描述和准确识别提供基础的同时,也亟需与之相应的大带宽大转角情况下的电磁模型参数提取方法。相比窄带条件,跨谱段信号数据量大,所含物理量信息维度高且复杂,大转角情况下距离和方位向耦合。该文提出跨谱段SAR散射中心多维参数解耦和估计方法,首先结合极坐标格式算法(PFA)和属性散射中心模型构造2维解耦波数域散射中心模型,再结合坐标下降法(CDA)将复杂的高维耦合参数估计方法简化为循环迭代的1维参数估计方法,有效降低字典维度和估计复杂度,并引入Hooke-Jeeves算法提高估计精度。最后根据各个散射中心的参数估计结果对它们的结构和位置进行识别,对仿真数据的处理实验验证了该文方法的有效性。Abstract: Microwave photonics radar generates cross-band signals with large bandwidth, providing a basis for precise electromagnetic characteristics description and accurate identification of targets. Meanwhile, a corresponding electromagnetic model parameter extraction method is urgently required in the case of large-bandwidth and wide-angle. For the same scene, the amount of return signals will increase considerably in cross-band condition comparing with narrow-bandwidth condition. Furthermore, the signals under cross-band condition may exhibit complex range-azimuth coupling. Under such a condition, it is of difficulty to estimate high dimensional physical parameters of scattering centers in the scene from return signals. To solve this problem, a multi-parameter estimation of cross-band SAR scattering centers method is proposed. The Polar Format Algorithm (PFA) and the attributed scattering center model are combined to construct a two-dimensional decoupled wavenumber domain model. With this scattering model, the estimation procedure is transformed into an optimization problem with multiple variables. This complex multi-variable optimization problem is divided into a set of single variable optimization problems by using the Coordinate Descent Algorithm (CDA). The separation effectively reduces dictionary dimensions and estimation complexity. Moreover, the Hooke-Jeeves algorithm is introduced to enhance estimation accuracy in each single variable optimization problem. Consequently, the proposed estimator for scattering parameters is not only efficient, but also accurate. The structure and location of each scattering center can be identified according to the parameter estimation results. Simulation results confirm the validity of the proposed method.
-
表 1 仿真模型参数估计结果
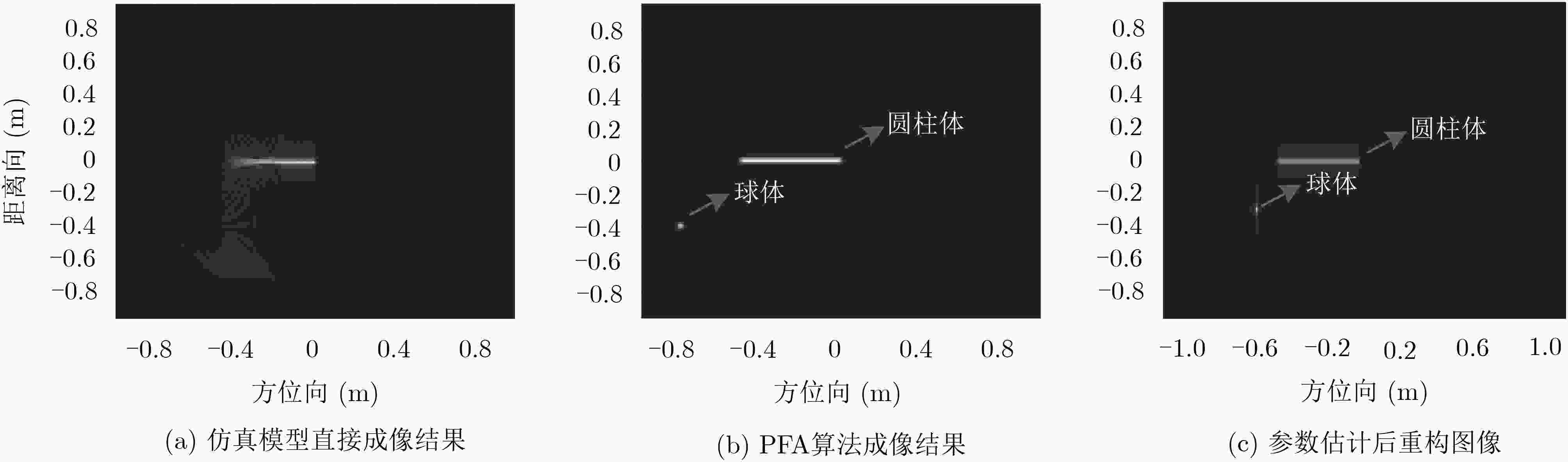
散射中心 $L\left( {\rm{m }}\right)$ ${\bar \varphi _0}\left( {{\rm{rad}}} \right)$ $\alpha $ $x\left( {\rm{m}} \right)$ $y\left( {\rm{m}} \right)$ $A$ 散射体结构 1 0.4512 –0.0045 0.5 –0.2530 0.0070 0.3881+0.0284i 圆柱体 2 0 0 0 –0.7970 0.3990 0.0012+0.0003i 球体 表 2 挖掘机散射中心参数估计结果
散射中心 1 2 3 4 5 6 7 $L\left( {\rm{m}} \right)$ 2.0695 2.0824 0.0723 0.1000 0.1000 0 0.1 $\alpha $ 0 0 0.5 0 0 0 –1 散射体结构 直边 直边 圆柱 直边 直边 球面 角衍射 散射中心 8 9 10 11 12 13 14 $L\left( {\rm{m}} \right)$ 0 0 0.2372 0.2200 0.0687 0 0 $\alpha $ 0 0.5 0 0 0.5 0 0.5 散射体结构 球面 帽顶 直边 直边 圆柱 球面 帽顶 -
潘时龙, 张亚梅. 微波光子雷达及关键技术[J]. 科技导报, 2017, 35(20): 36–52. doi: 10.3981/j.issn.1000-7857.2017.20.004PAN Shilong and ZHANG Yamei. Microwave photonic radar and key technologies[J]. Science &Technology Review, 2017, 35(20): 36–52. doi: 10.3981/j.issn.1000-7857.2017.20.004 杨利超, 邢孟道, 孙光才, 等. 一种微波光子雷达ISAR成像新方法[J]. 电子与信息学报, 2019, 41(6): 1271–1279. doi: 10.11999/JEIT180661YANG Lichao, XING Mengdao, SUN Guangcai, et al. A novel ISAR imaging algorithm for microwave photonics radar[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1271–1279. doi: 10.11999/JEIT180661 陈潇翔, 邢孟道, 孙光才, 等. 一种超宽带10 GHz微波光子雷达包络与相位联合运动误差估计方法[J]. 电子与信息学报, 2019, 41(5): 1069–1076. doi: 10.11999/JEIT180563CEHN Xiaoxiang, XING Mengdao, SUN Guangcai, et al. A motion error estimation method joint envelope and phase for 10 GHz ultra-wideband microwave photonic-based SAR image[J]. Journal of Electronics and Information Technology, 2019, 41(5): 1069–1076. doi: 10.11999/JEIT180563 DING Baiyuan and WEN Gongjian. Target reconstruction based on 3-D scattering center model for robust SAR ATR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(7): 3772–3785. doi: 10.1109/TGRS.2018.2810181 文贡坚, 朱国强, 殷红成, 等. 基于三维电磁散射参数化模型的SAR目标识别方法[J]. 雷达学报, 2017, 6(2): 115–135. doi: 10.12000/JR17034WEN Gongjian, ZHU Guoqiang, YIN Hongcheng, et al. SAR ATR based on 3D parametric electromagnetic scattering model[J]. Journal of Radars, 2017, 6(2): 115–135. doi: 10.12000/JR17034 段佳, 张磊, 盛佳恋, 等. 独立属性散射中心参数降耦合估计方法[J]. 电子与信息学报, 2012, 34(8): 1853–1859. doi: 10.3724/SP.J.1146.2011.01302DUAN Jia, ZHANG Lei, SHENG Jialian, et al. Parameters decouple and estimation of independent attributed scattering centers[J]. Journal of Electronics &Information Technology, 2012, 34(8): 1853–1859. doi: 10.3724/SP.J.1146.2011.01302 蒋文, 李王哲. 基于幅相分离的属性散射中心参数估计新方法[J]. 雷达学报, 2019, 8(5): 606–615. doi: 10.12000/JR18097JIANG Wen and LI Wangzhe. A new method for parameter estimation of attributed scattering centers based on amplitude-phase separation[J]. Journal of Radars, 2019, 8(5): 606–615. doi: 10.12000/JR18097 段佳, 张磊, 邢孟道, 等. 合成孔径雷达目标特征提取新方法[J]. 西安电子科技大学学报: 自然科学版, 2014, 41(4): 13–19. doi: 10.3969/j.issn.1001-2400.2014.04.003DUAN Jia, ZHANG Lei, XING Mengdao, et al. Novel feature extraction method for synthetic aperture radar targets[J]. Journal of Xidian University:Natural Science, 2014, 41(4): 13–19. doi: 10.3969/j.issn.1001-2400.2014.04.003 李飞, 纠博, 刘宏伟, 等. 基于稀疏表示的SAR图像属性散射中心参数估计算法[J]. 电子与信息学报, 2014, 36(4): 931–937. doi: 10.3724/SP.J.1146.2013.00576LI Fei, JIU Bo, LIU Hongwei, et al. Sparse representation based algorithm for estimation of attributed scattering center parameter on SAR imagery[J]. Journal of Electronics &Information Technology, 2014, 36(4): 931–937. doi: 10.3724/SP.J.1146.2013.00576 LIU Hongwei, JIU Bo, LI Fei, et al. Attributed scattering center extraction algorithm based on sparse representation with dictionary refinement[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(5): 2604–2614. doi: 10.1109/TAP.2017.2673764 符吉祥, 孙光才, 邢孟道. 一种大转角ISAR两维自聚焦平动补偿方法[J]. 电子与信息学报, 2017, 39(12): 2889–2898. doi: 10.11999/JEIT170303FU Jixiang, SUN Guangcai, and XING Mengdao. A two dimensional autofocus translation compensation method for wide-angle ISAR imaging[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2889–2898. doi: 10.11999/JEIT170303 POTTER L C and MOSES R L. Attributed scattering centers for SAR ATR[J]. IEEE Transactions on Image Processing, 1997, 6(1): 79–91. doi: 10.1109/83.552098 POTTER L C, CHIANG D M, CARRIERE R, et al. A GTD-Based parametric model for radar scattering[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1058–1067. doi: 10.1109/8.467641 GERRY M J, POTTER L C, GUPTA I J, et al. A parametric model for synthetic aperture radar measurements[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(7): 1179–1188. doi: 10.1109/8.785750 李飞. 雷达图像目标特征提取方法研究[D]. [博士论文], 西安电子科技大学, 2014.LI Fei. Study on target feature extraction based on radar image[D]. [Ph. D. dissertation], Xidian University, 2014. 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 82–85. NOCEDAL J and WRIGHT S J. Numerical Optimization[M]. New York: Springer, 54–55. THOMAS K J and ALAA K A. Monotonic iterative algorithm for minimum-entropy autofocus[C]. IEEE International Conference on Image Processing, Atlanta, USA, 2006: 645–648. HOOKE R and JEEVES T A. “Direct Search” solution of numerical and statistical problems[J]. Journal of the ACM, 1961, 8(2): 212–229. doi: 10.1145/321062.321069 FLETCHER R. Practical Methods of Optimization[M]. 2nd ed. New York: John Wiley & Sons, 1987: 18–19. -





 下载:
下载:



 下载:
下载:
