Robust Energy Efficiency Optimization Algorithm for NOMA-based D2D Communication With Simultaneous Wireless Information and Power Transfer
-
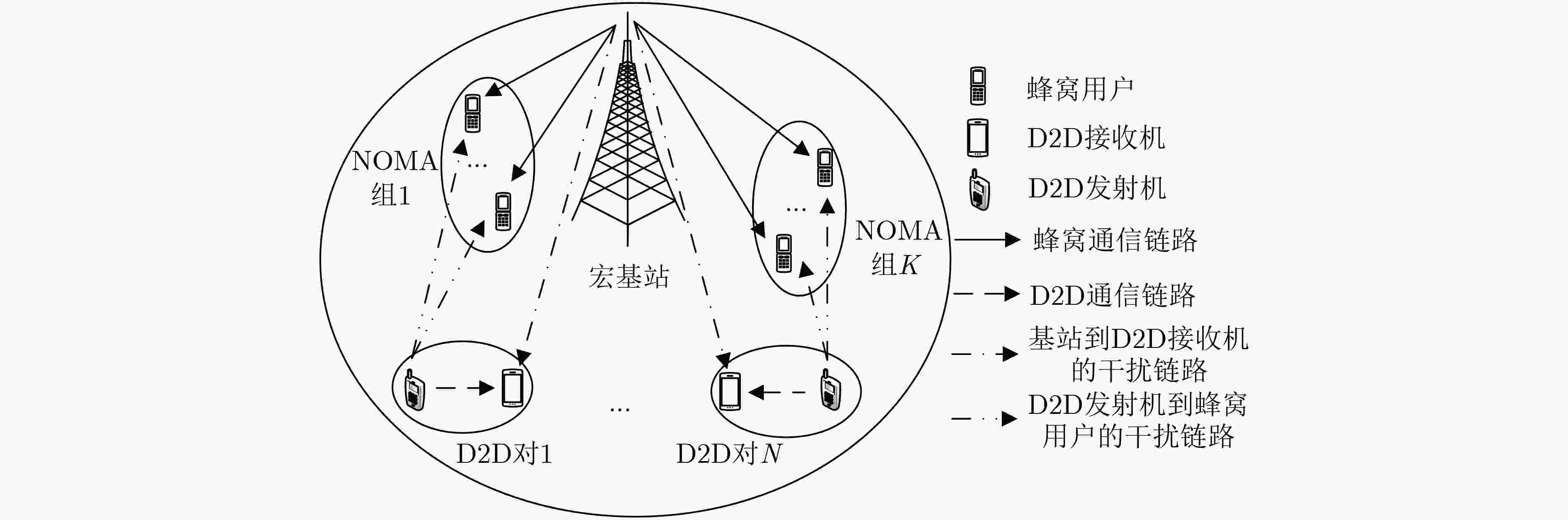
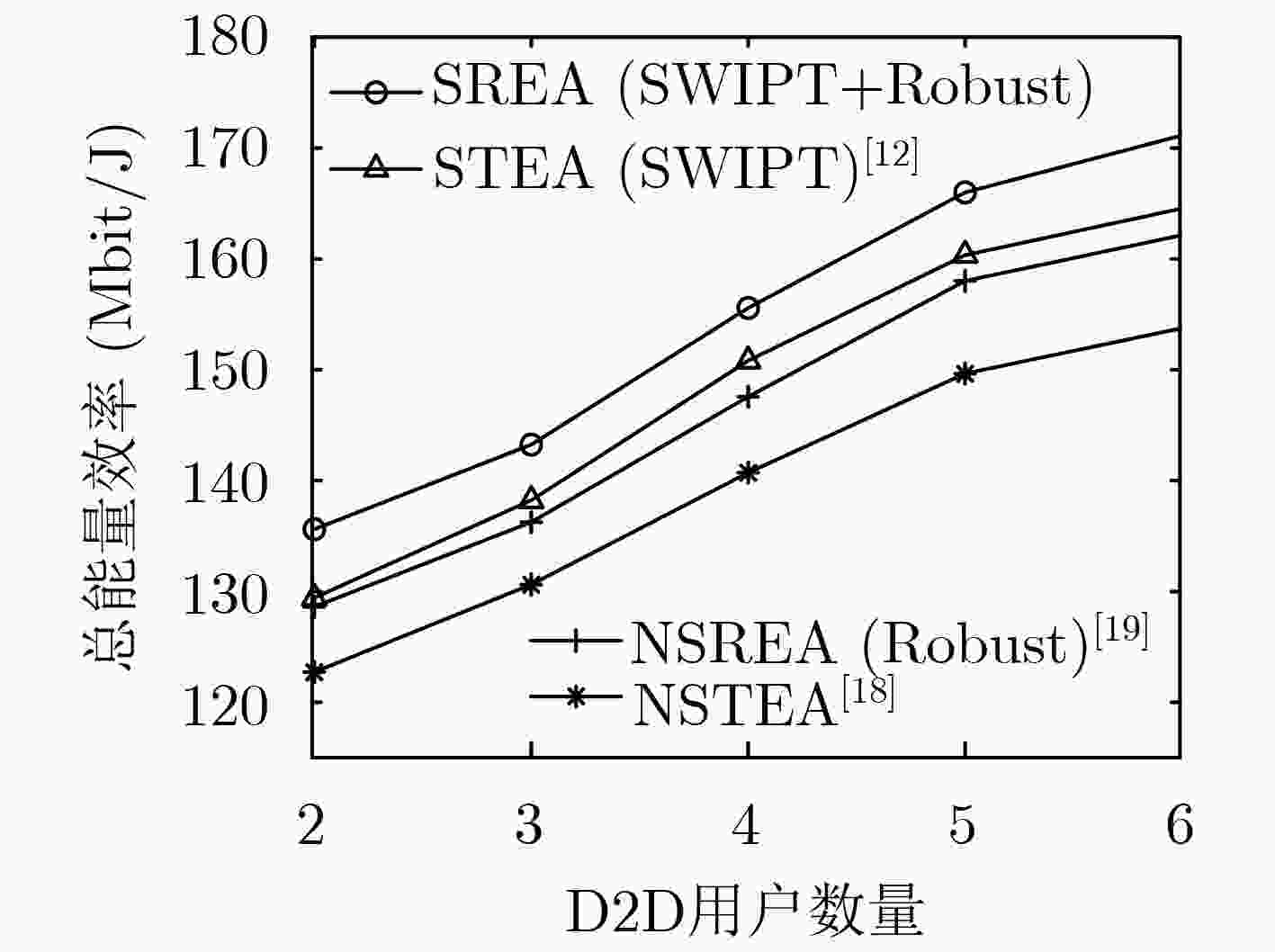
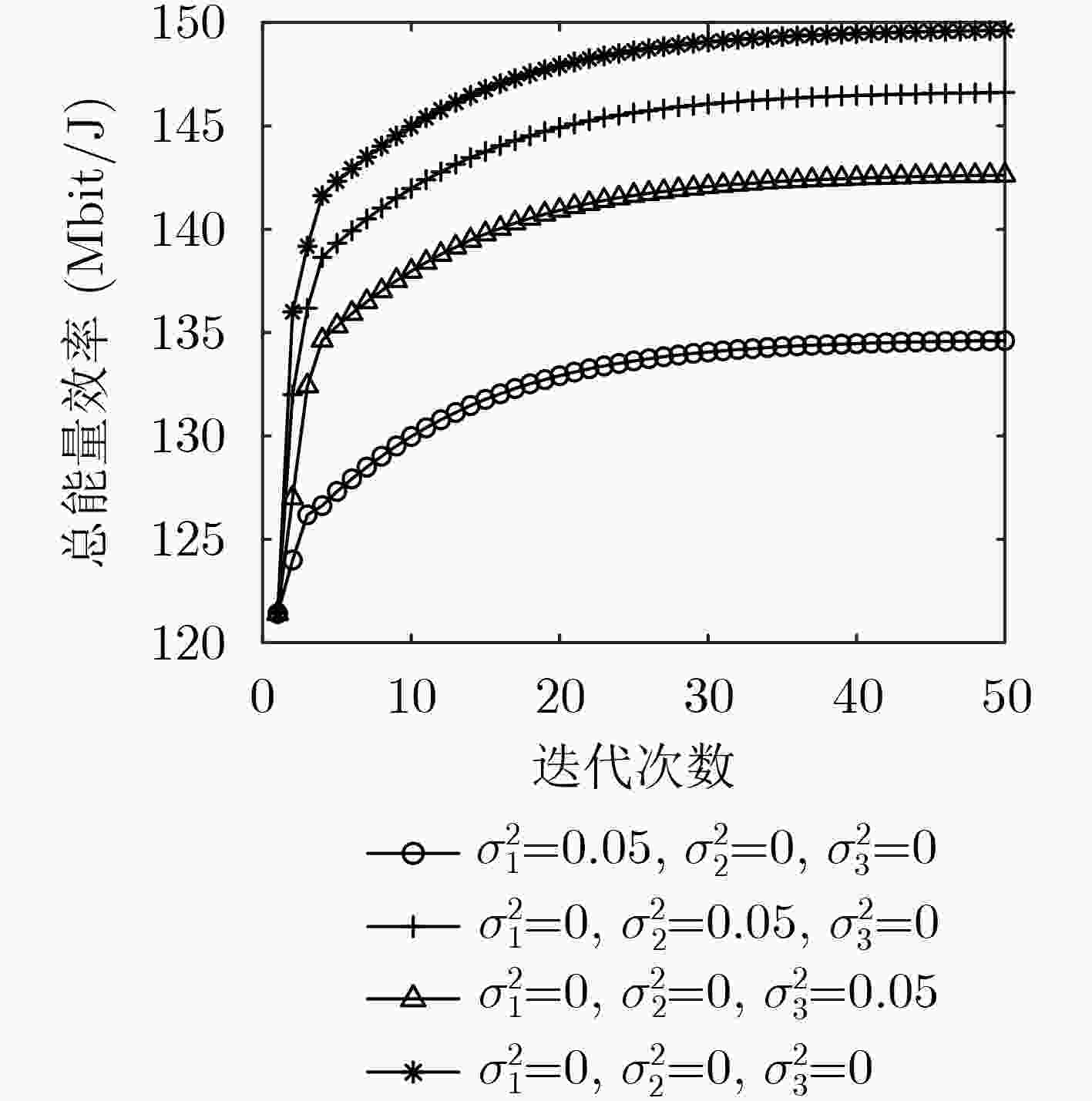
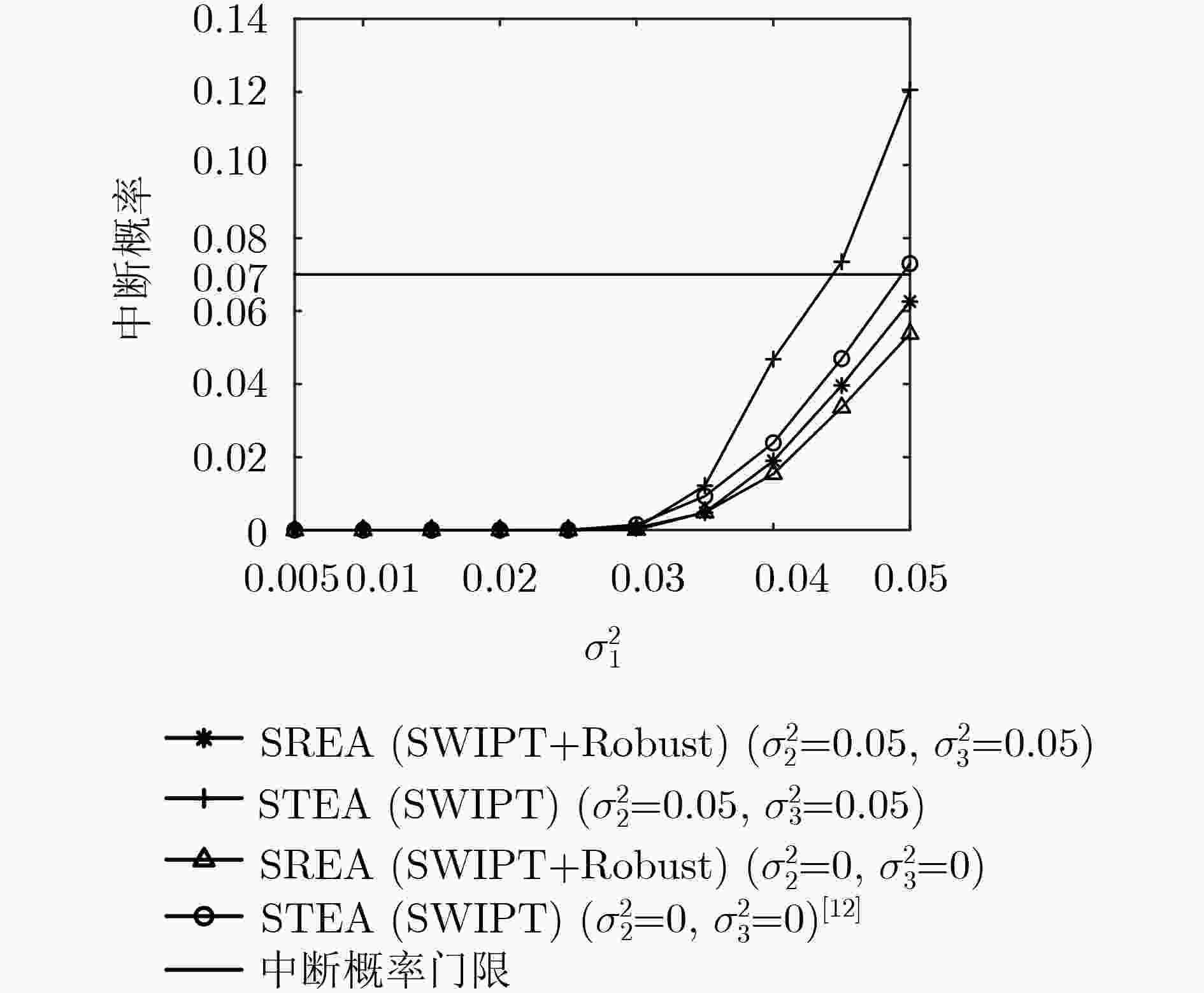
摘要: 针对频谱短缺、基站负荷过高、通信系统功耗较大等问题,考虑不完美的信道状态信息,该文提出一种基于非正交多址接入的无线携能(SWIPT)D2D网络鲁棒能效(EE)最大化资源分配算法(SREA)。考虑用户的服务质量约束以及最大发射功率约束,基于随机信道不确定性建立鲁棒能效最大化资源分配模型。利用Dinkelbach和变量替换方法,将原NP-hard问题转换为确定性的凸优化问题,通过拉格朗日对偶理论求得解析解。仿真结果表明,所提算法在保证蜂窝用户通信质量的同时,能够有效提高D2D用户的能效性和鲁棒性能。Abstract: In order to resolve the problems of spectrum shortage, large power consumption, and excessive load at base stations, a Simultaneous Wireless Information and Power Transfer (SWIPT)-based Robust Energy Efficiency (EE) Algorithm (SREA) with imperfect channel state information is proposed to maximize the total EE in Non-Orthogonal Multiple Access (NOMA) assisted Device-to-Device (D2D) networks. Considering the users' Quality of Service (QoS) constraints and maximum transmit power constraints, a robust EE maximization-based resource allocation model is established based on random channel uncertainties. Moreover, the original NP-hard problem is transformed into a deterministic convex optimization problem by using Dinkelbach’s method and the variable substitution method. And the analytical solutions are obtained through Lagrange dual theory. Simulation results demonstrated that the proposed algorithm can effectively improve the system EE and the robustness of D2D users while ensuring the communication quality of cellular users.
-
表 1 系统参数
参数 含义 $N$ D2D用户数量 $\theta $ 能量收集效率系数 $P_{}^{\max }$ 基站的最大发射功率 ${M_k}$ 资源块$k$上的蜂窝用户数量 $P_n^{\max }$ D2D用户$n$的最大发射功率 $h_n^k$ D2D用户$n$在资源块$k$上的信道增益 $q_n^k$ D2D用户$n$在资源块$k$上的发射功率 $h_i^{k,C}$ 基站到蜂窝用户$i$在资源块$k$上的信道增益 $g_n^{k,B}$ 基站到D2D用户$n$在资源块$k$上的信道增益 $K$ 资源块数量 $\tau $ 中断概率门限 $M$ 蜂窝用户总数量 ${\sigma ^2}$ 接收机的背景噪声功率 $P_c^D$ D2D用户的电路功率消耗 $R_i^{k,\min }$ 蜂窝用户$i$的最小数据速率 $p_i^k$ 基站通过资源块$k$分配给蜂窝用户$i$的发射功率 $g_{n,i}^k$ D2D用户$n$到蜂窝用户$i$在资源块$k$上的信道增益 $g_{d,n}^k$ D2D用户$d$到D2D用户$n$在资源块$k$上的信道增益 表 2 鲁棒资源分配算法
初始化系统参数$N$, ${M_k}$, $M$, $K$, $P_c^D$, ${\sigma ^2}$, $\theta $, $\tau $, $R_n^{\min }$, $R_i^{k,\min }$, $P_n^{\max }$, $P_{}^{\max }$, $d$;给定$p_n^k$, $x_n^k$, $\eta $, $\rho _{n,1}^k$, $\rho _{n,2}^k$;外层迭代次数$t = 0$;定义算法
收敛精度$\varpi $和$\varsigma $,外层最大迭代次数$T$;(1) While $\left| {\dfrac{ {\tilde R(t)} }{ {\tilde P(t)} } - \eta (t - 1)} \right| > \varpi$和$t < T$, do (2) 初始化迭代步长和拉格朗日乘子,定义内层最大迭代次数$L$,初始化$l = 0$; (3) While $\left| {q_n^k(l) - q_n^k(l - 1)} \right| > \varsigma $和$l < L$,do (4) For $m = 1:1:M$ (5) For $n = 1:1:N$ (6) For $k = 1:1:K$ (7) 根据式(26)计算$T_n^k$,更新$x_n^k$; (8) 根据式(29)计算$\alpha _n^k$; (9) 计算$\rho _{n,1}^k$,$\rho _{n,2}^k$, $q_n^k$的最优值; (10) 根据式(30)—式(34)更新拉格朗日乘子; (11) End For (12) End For (13) End For (14) 更新 $l = l + 1$; (15) End While
(16) 更新$\eta (t) = \dfrac{ {\tilde R(t)} }{ {\tilde P(t)} }$, $t = t + 1$;(17) End While -
[1] LEE N, LIN Xingqin, ANDREWS J G, et al. Power control for D2D underlaid cellular networks: Modeling, algorithms, and analysis[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(1): 1–13. doi: 10.1109/JSAC.2014.2369612 [2] PERERA T D P, JAYAKODY D N K, SHARMA S K, et al. Simultaneous wireless information and power transfer (SWIPT): Recent advances and future challenges[J]. IEEE Communications Surveys & Tutorials, 2018, 20(1): 264–302. doi: 10.1109/COMST.2017.2783901 [3] 高东, 梁子林. 基于能量效率的双层非正交多址系统资源优化算法[J]. 电子与信息学报, 2020, 42(5): 1237–1243. doi: 10.11999/JEIT190048GAO Dong and LIANG Zilin. Energy efficient based resource optimization algorithm for two-tier non-orthogonal multiple access network[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1237–1243. doi: 10.11999/JEIT190048 [4] PAN Yijin, PAN Cunhua, YANG Zhaohui, et al. Resource allocation for D2D communications underlaying a NOMA-based cellular network[J]. IEEE Wireless Communications Letters, 2018, 7(1): 130–133. doi: 10.1109/LWC.2017.2759114 [5] CHEN Jian, JIA Jie, LIU Yuanwei, et al. Optimal resource block assignment and power allocation for D2D-enabled NOMA communication[J]. IEEE Access, 2019, 7: 90023–90035. doi: 10.1109/ACCESS.2019.2926438 [6] SALEEM U, JANGSHER S, QURESHI H K, et al. Joint subcarrier and power allocation in the energy-harvesting-aided D2D communication[J]. IEEE Transactions on Industrial Informatics, 2018, 14(6): 2608–2617. doi: 10.1109/TII.2018.2794467 [7] DAI Yanpeng, SHENG Min, LIU Junyu, et al. Joint mode selection and resource allocation for D2D-enabled NOMA cellular networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 6721–6733. doi: 10.1109/TVT.2019.2916395 [8] ZHENG Hanyu, HOU Shujuan, LI Hai, et al. Power allocation and user clustering for uplink MC-NOMA in D2D underlaid cellular networks[J]. IEEE Wireless Communications Letters, 2018, 7(6): 1030–1033. doi: 10.1109/LWC.2018.2845398 [9] SUN Huakui, ZHAI Daosen, ZHANG Zhenfeng, et al. Channel allocation and power control for device-to-device communications underlaying cellular networks incorporated with non-orthogonal multiple access[J]. IEEE Access, 2019, 7: 168593–168605. doi: 10.1109/ACCESS.2019.2954467 [10] ZHAI Daosen, ZHANG Ruonan, WANG Yutong, et al. Joint user pairing, mode selection, and power control for D2D-capable cellular networks enhanced by nonorthogonal multiple access[J]. IEEE Internet of Things Journal, 2019, 6(5): 8919–8932. doi: 10.1109/JIOT.2019.2924513 [11] CHEN Bo, LIU Juan, YANG Xinjie, et al. Resource allocation for energy harvesting-powered D2D communications underlaying NOMA-based networks[J]. IEEE Access, 2019, 7: 61442–61451. doi: 10.1109/ACCESS.2019.2913041 [12] PEI Lu, YANG Zhaohui, PAN Cunhua, et al. Energy-efficient D2D communications underlaying NOMA-based networks with energy harvesting[J]. IEEE Communications Letters, 2018, 22(5): 914–917. doi: 10.1109/LCOMM.2018.2811782 [13] XU Yongjun, ZHAO Xiaohui, and LIANG Yingchang. Robust power control and beamforming in cognitive radio networks: A survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 1834–1857. doi: 10.1109/COMST.2015.2425040 [14] WANG Xiaoming, ZHENG Fuchun, ZHU Pengcheng, et al. Energy-efficient resource allocation in coordinated downlink multicell OFDMA systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1395–1408. doi: 10.1109/TVT.2015.2413950 [15] DINKELBACH W. On nonlinear fractional programming[J]. Management Science, 1967, 13(7): 492–498. doi: 10.1287/mnsc.13.7.492 [16] BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004: 61–102. [17] 李国权, 徐勇军, 陈前斌. 基于干扰效率多蜂窝异构无线网络最优基站选择及功率分配算法[J]. 电子与信息学报, 2020, 42(4): 957–964. doi: 10.11999/JEIT190419LI Guoquan, XU Yongjun, and CHEN Qianbin. Interference efficiency-based base station selection and power allocation algorithm for multi-cell heterogeneous wireless networks[J]. Journal of Electronics &Information Technology, 2020, 42(4): 957–964. doi: 10.11999/JEIT190419 [18] ALEMAISHAT S, SARAEREH O A, KHAN I, et al. An efficient resource allocation algorithm for D2D communications based on NOMA[J]. IEEE Access, 2019, 7: 120238–120247. doi: 10.1109/ACCESS.2019.2937401 [19] HAO Yuanyuan, NI Qiang, LI Hai, et al. Robust multi-objective optimization for EE-SE tradeoff in D2D communications underlaying heterogeneous networks[J]. IEEE Transactions on Communications, 2018, 66(10): 4936–4949. doi: 10.1109/TCOMM.2018.2834920 -





 下载:
下载:


 下载:
下载:
