基于效用最大化的无线可充电传感器网络有向充电调度方案

王杨; 张鑫; 赵传信; 方群; 艾世成

doi:10.11999/JEIT200129

基于效用最大化的无线可充电传感器网络有向充电调度方案

doi: 10.11999/JEIT200129

王杨^1, ,,
张鑫¹,
赵传信¹,
方群¹,
艾世成²

1.
安徽师范大学计算机与信息学院芜湖 241002
2.
东南大学计算机科学与工程学院南京 211189

基金项目: 国家自然科学基金(61871412)，安徽省自然科学基金重点项目(KJ2019A0938)，安徽省社科规划基金(AHSKY2017D42)，安徽高校自然科学重点项目研究项目(KJ2017A552, KJ2019A0979)

详细信息

作者简介:
王杨：男，1971年生，教授，硕士生导师，研究方向为可充电传感网、机器学习、系统优化

张鑫：男，1996年生，硕士生，研究方向为可充电传感网

赵传信：男，1977年生，教授，博士生导师，研究方向可充电传感网

方群：男，1972年生，教授，硕士生导师，研究方向为物联网

艾世成：男，1994年生，硕士生，研究方向为网络优化

通讯作者:
王杨　wycap@126.com

中图分类号: TP393
计量
- 文章访问数: 1225
- HTML全文浏览量: 342
- PDF下载量: 100
- 被引次数: 0
出版历程
- 收稿日期: 2020-02-26
- 修回日期: 2020-11-26
- 网络出版日期: 2020-12-02
- 刊出日期: 2021-05-18

Directional Charging Schedule Scheme Based on Charging Utility Maximization for Wireless Rechargeable Sensor Network

1.
School of Computer and Information, Anhui Normal University, Wuhu 241002, China
2.
School of Computer Science and Engineering, Southeast University, Nanjing 211189, China

Funds: The National Natural Science Foundation of China (61871412), The Key Project of Natural Science Foundation of Anhui Province (KJ2019A0938), Anhui Province Major Humanities and Social Science Fund Project (AHSKY2017D42), The Key Natural Science Projects of Anhui University (KJ2017A552, KJ2019A0979)

摘要

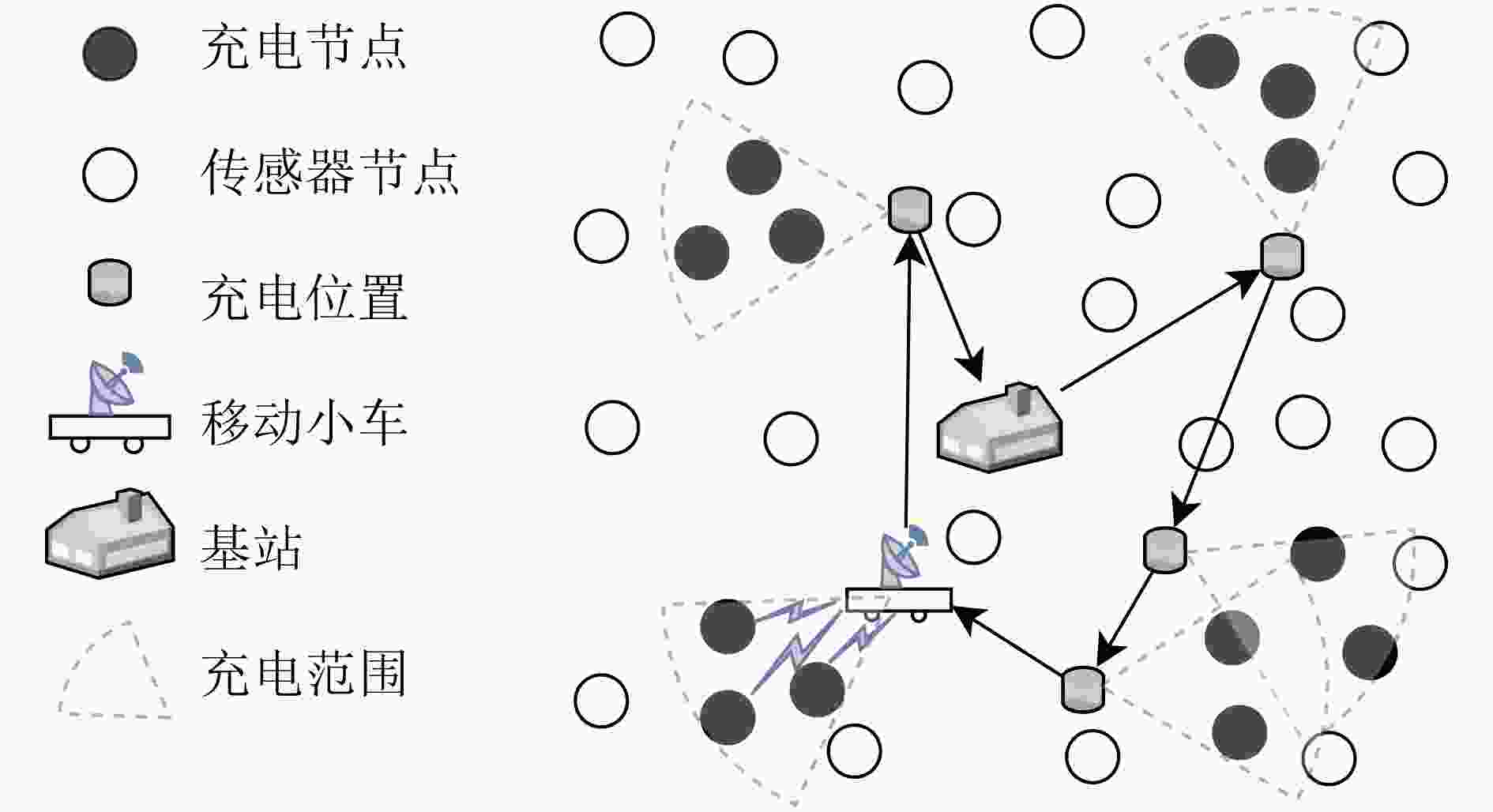
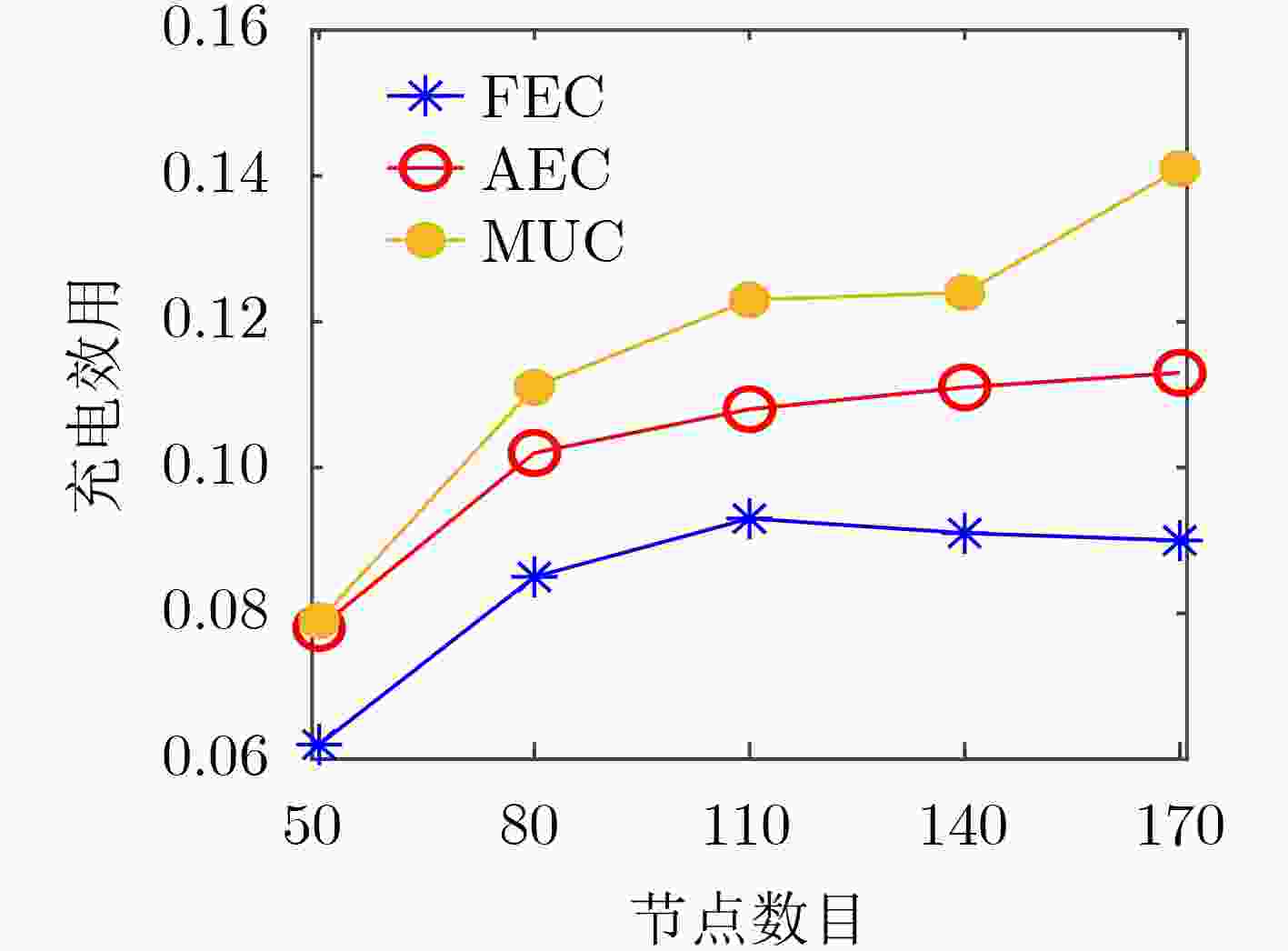
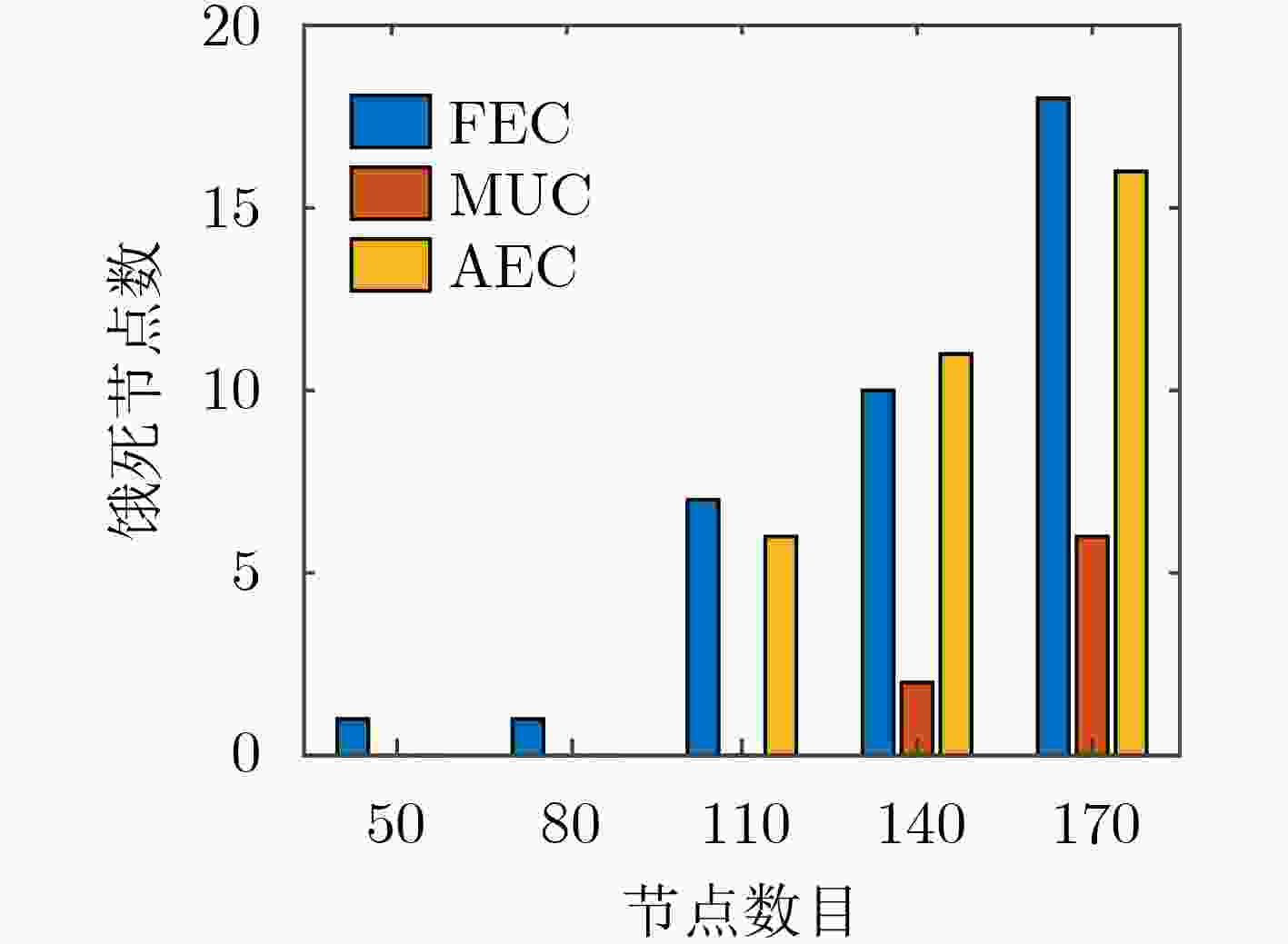
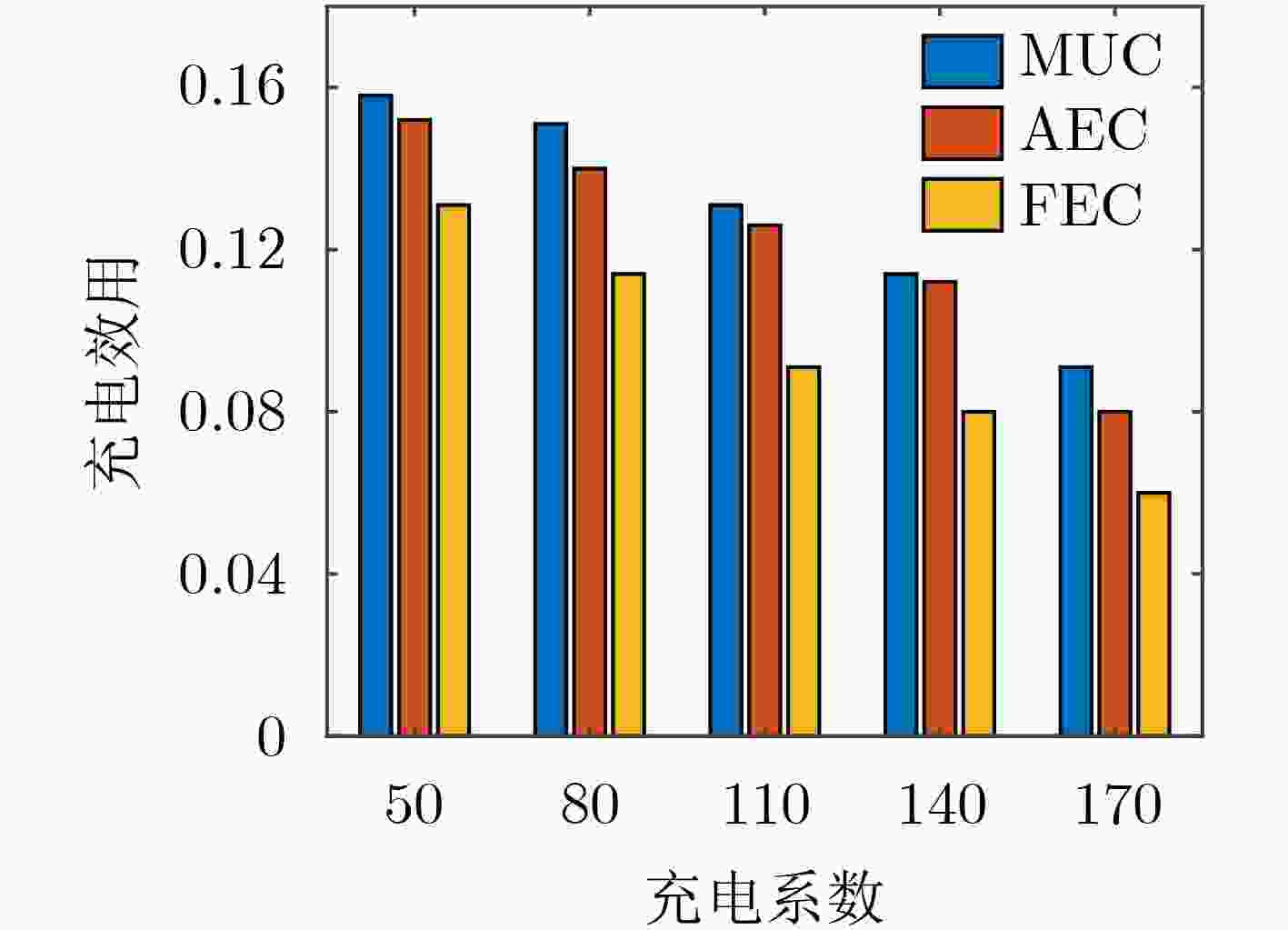
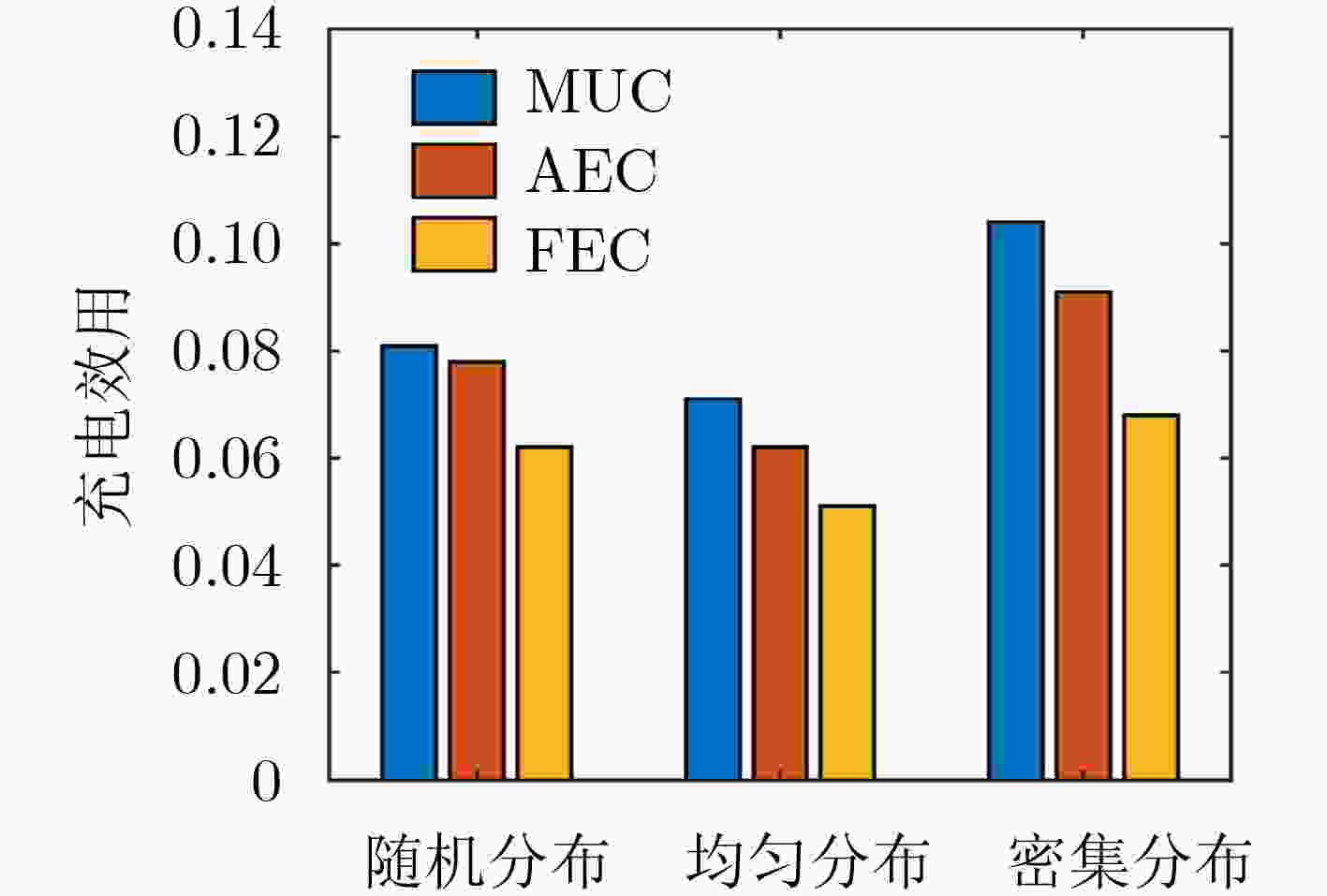
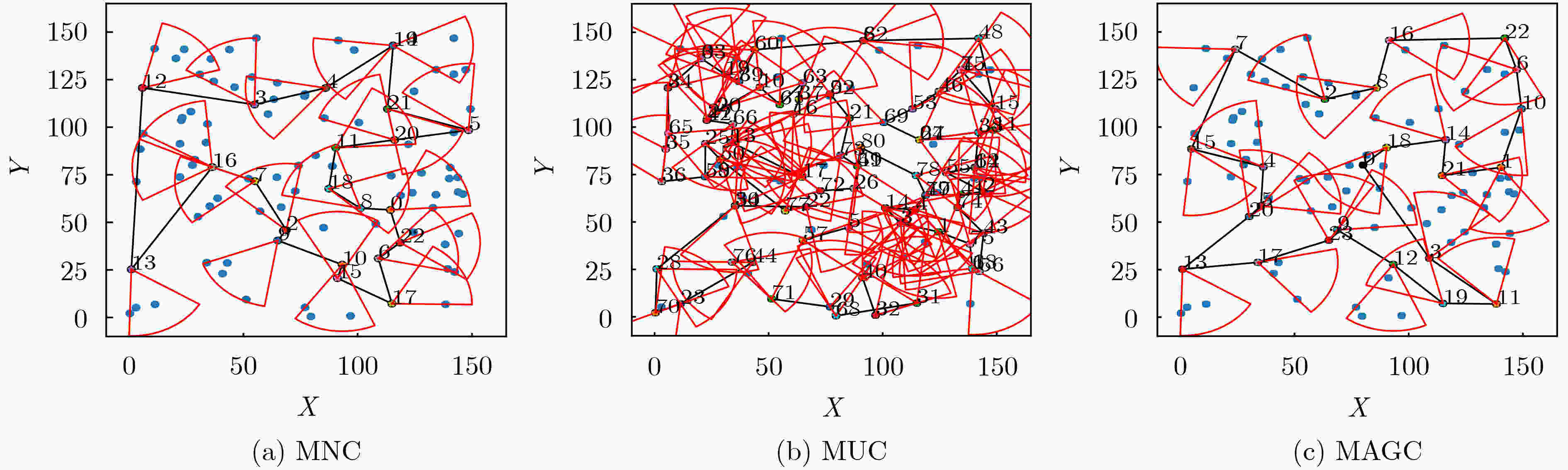
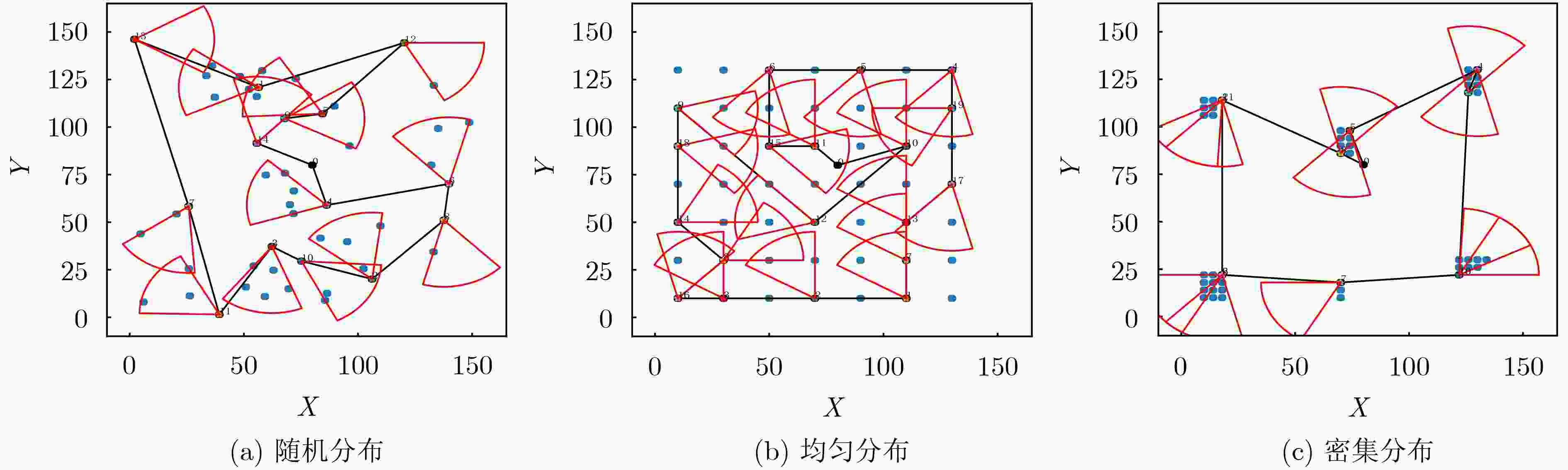
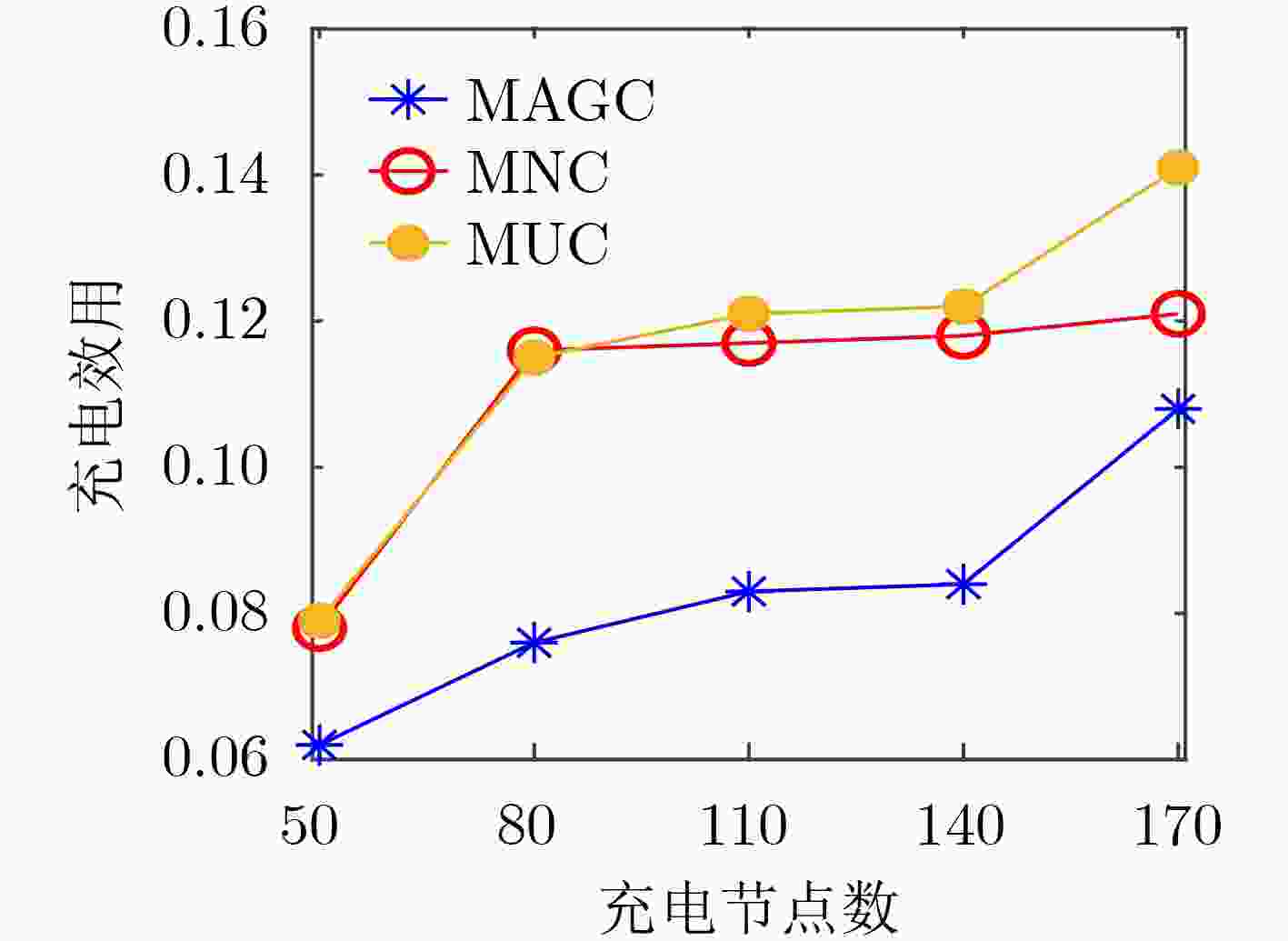
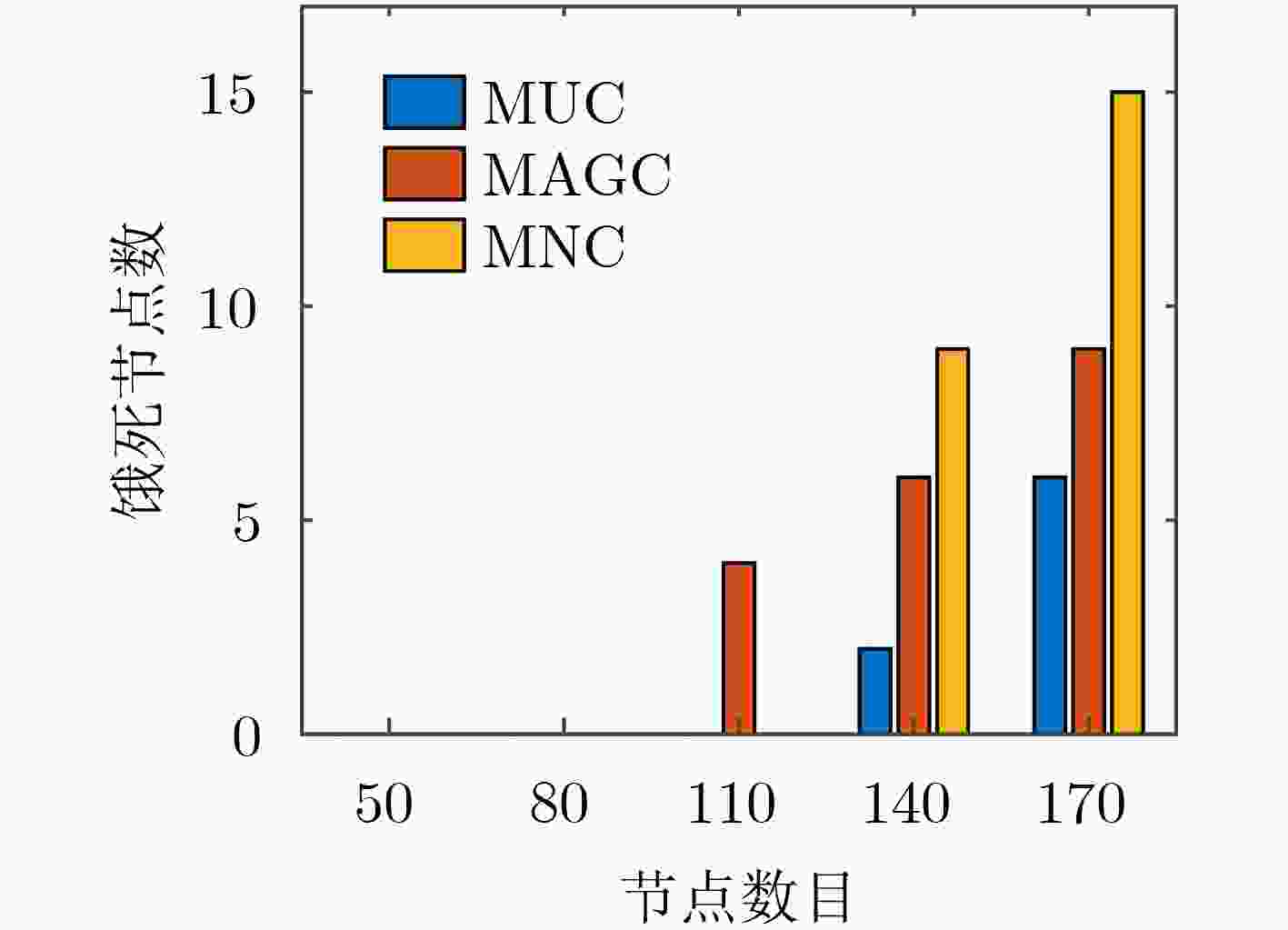
摘要: 针对当前无线可充电传感器网络(WRSNs)一对一移动充电方式存在充电效率低、定向充电模型缺乏问题，该文提出了一种基于充电效用最大化(MUC)的一对多有向充电调度方案。方案首先筛选网络中充电增益最大的有向覆盖子集；然后根据有向覆盖子集确定充电锚点，并进而规划充电器的移动路径；最后在满足移动充电器能量和充电周期约束条件下优化移动充电器的充电时间。实验结果表明，该方案与平均能量充电(AEC)、固定能量充电(FEC)相比，充电效率分别提高了13.7%和32.7%；与最多节点覆盖(MNC)、最大平均增益覆盖(MAGC)子集筛选方案相比，充电效率分别提高了4.4%和35.9%；同时在网络饿死节点数目上与MNC, MAGC方案相比也显著降低。
- 无线可充电传感器网络 /
- 充电效用最大化 /
- 有向充电 /
- 有向覆盖子集
Abstract: The one-to-one charging method for Wireless Rechargeable Sensor Networks (WRSNs) mobile chargers has some problems such as low charging efficiency and lack of directional charging model. To cope with the problems, a one-to-many directed charging scheduling scheme based on Maximizing Utility Charging (MUC) is proposed. In this scheme, the directed coverage subsets with the largest charging gain in the network is first searched; Then the charging anchor points are determined according to the directed coverage subset and the charger movement path is planned; Finally, the constraints of mobile charger energy and charging cycle are considered and the charging time is optimized. Experimental results show that in comparation with Average Energy Charge (AEC) and Fixed Energy Charge (FEC) charging time optimization schemes, the charging efficiency of this scheme is increased by 13.7% and 32.7% respectively. In comparation with Maximum Node Coverage (MNC) and Maximum Average Gain Coverage (MAGC) subset screening schemes, the charging efficiency is increased by 4.4% and 35.9% respectively. In addition, the number of starved nodes in the network is significantly reduced compared with the MNC, MAGC schemes.
- Wireless Rechargeable Sensor Network(WRSN) /
- Maximum Utility Charging(MUC) /
- Directional charge /
- Directed coverage subset

HTML全文

图 1 网络系统模型

下载: 全尺寸图片幻灯片

图 2 有向充电模型

下载: 全尺寸图片幻灯片

图 3 覆盖集合提取示例图

下载: 全尺寸图片幻灯片

图 4 电池充电获能图

下载: 全尺寸图片幻灯片

图 5 不同规模下算法充电效用对比图

下载: 全尺寸图片幻灯片

图 6 不同节点规模下充电算法饿死节点数对比图

下载: 全尺寸图片幻灯片

图 7 参数$p$对不同充电算法的影响

下载: 全尺寸图片幻灯片

图 8 不同节点分布对充电算法的影响

下载: 全尺寸图片幻灯片

图 9 不同覆盖算法下覆盖子集筛选图

下载: 全尺寸图片幻灯片

图 10 不同节点分布下覆盖子集筛选图

下载: 全尺寸图片幻灯片

图 11 不同节点规模下子集筛选算法充电效用对比图

下载: 全尺寸图片幻灯片

图 12 不同节点规模下子集筛选算法饿死节点数对比图

下载: 全尺寸图片幻灯片

表 1 参数设置

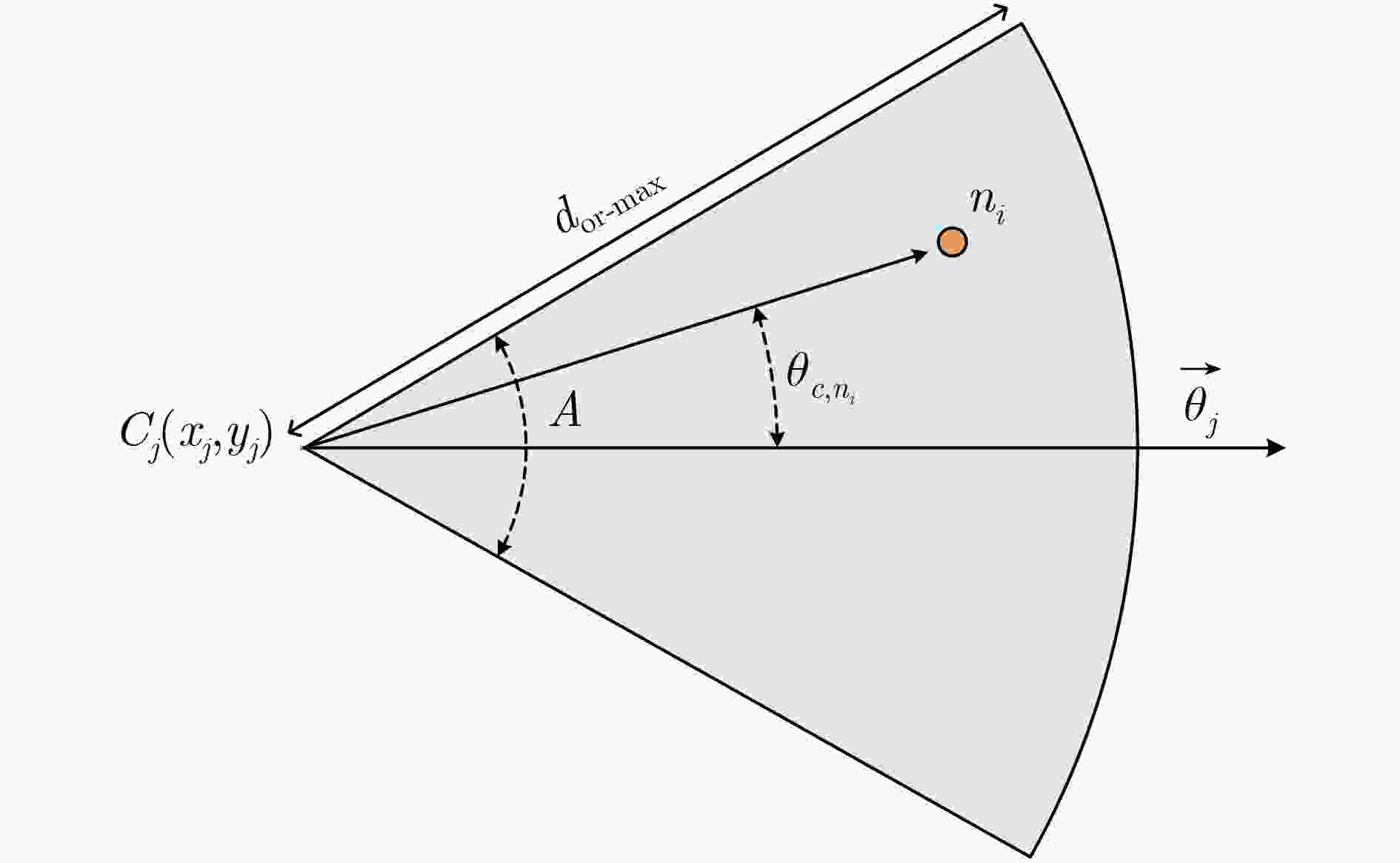
参数	值
移动充电器能量EI	80000 J
传感器能量B	1000 J
移动充电器移动速度v	2 m/s
移动充电器移动能耗C_v	5 J/s
移动充电器充电能耗C	2 J/s
充电周期T	60 min
充电参数p	200
最大充电距离D	35 m
有向覆盖角A	π/3

下载: 导出CSV

参考文献(21)

[1]	HU Cheng and WANG Yun. Minimizing the number of mobile chargers in a large-scale wireless rechargeable sensor network[C]. 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, USA, 2015: 1297–1302. doi: 10.1109/WCNC.2015.7127656.
[2]	HARICHANDAN P, JAISWAL A, and KUMAR S. Multiple Aggregator Multiple Chain routing protocol for heterogeneous wireless sensor networks[C]. 2013 International Conference on Signal Processing and Communication (ICSC), Noida, India, 2013: 127–131. doi: 10.1109/ICSPCom.2013.6719769.
[3]	PRADEEBAA G and LAVANIS N. Network lifetime improvement using routing algorithm with sleep mode in wireless sensor network[C]. 2016 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 2016: 1572–1575. doi: 10.1109/WiSPNET.2016.7566401.
[4]	YUE Yinggao, FAN Hehong, LI Jianqing, et al. Large-scale mobile wireless sensor network data fusion algorithm[C]. 2016 IEEE International Conference on Big Data Analysis (ICBDA), Hangzhou, China, 2016: 1–5. doi: 10.1109/ICBDA.2016.7509832.
[5]	刁鹏飞, 王艳娇. 基于节点休眠的水下无线传感器网络覆盖保持分簇算法[J]. 电子与信息学报, 2018, 40(5): 1101–1107. doi: 10.11999/JEIT170787 DIAO Pengfei and WANG Yanjiao. Coverage-preserving clustering algorithm for underwater sensor networks based on the sleeping mechanism[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1101–1107. doi: 10.11999/JEIT170787
[6]	SHARMA H, HAQUE A, and JAFFERY Z A. An efficient solar energy harvesting system for wireless sensor nodes[C]. The 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 2018: 461–464. doi: 10.1109/ICPEICES.2018.8897434.
[7]	JUSHI A, PEGATOQUET A, and LE T N. Wind energy harvesting for autonomous wireless sensor networks[C]. 2016 Euromicro Conference on Digital System Design (DSD), Limassol, Cyprus, 2016: 301–308. doi: 10.1109/DSD.2016.43.
[8]	LEBAHN F and EWALD H. Using atmospheric temperature variations for thermal energy harvesting for wireless sensors[C]. The 9th International Conference on Sensing Technology (ICST), Auckland, New Zealand, 2015: 133–137. doi: 10.1109/ICSensT.2015.7438378.
[9]	TONG Bin, LI Zi, WANG Guiling, et al. How wireless power charging technology affects sensor network deployment and routing[C]. The IEEE 30th International Conference on Distributed Computing Systems, Genova, Italy, 2010: 438–447. doi: 10.1109/ICDCS.2010.61.
[10]	TOMAR A, KASWAN A, and JANA P K. On-demand energy provisioning in wireless sensor networks with capacity-constrained mobile chargers[C]. The 11th International Conference on Contemporary Computing (IC3), Noida, India, 2018: 1–6. doi: 10.1109/IC3.2018.8530654.
[11]	SHI Yi, XIE Liguang, HOU Y T, et al. On renewable sensor networks with wireless energy transfer[C]. 2011 IEEE INFOCOM, Shanghai, China, 2011: 1350–1358. doi: 10.1109/INFCOM.2011.5934919.
[12]	戴海鹏, 陈贵海, 徐力杰, 等. 一种高效有向无线充电器的布置算法[J]. 软件学报, 2015, 26(7): 1711–1729. doi: 10.13328/j.cnki.jos.004618 DAI Haipeng, CHEN Guihai, XU Lijie, et al. Effective algorithm for placement of directional wireless chargers[J]. Journal of Software, 2015, 26(7): 1711–1729. doi: 10.13328/j.cnki.jos.004618
[13]	ZHAO Chuanxin, ZHANG Xin, WU Changzhi, et al. Design of optimal utility of wireless rechargeable sensor networks via joint spatiotemporal scheduling[J]. Applied Mathematical Modelling, 2020, 86: 54–73. doi: 10.1016/j.apm.2020.05.009
[14]	HUONG T T, LE NGUYEN P, BINH H T T, et al. Genetic algorithm-based periodic charging scheme for energy depletion avoidance in WRSNs[C]. 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea (South), 2020: 1–6. doi: 10.1109/WCNC45663.2020.9120800.
[15]	ZHAO Chuanxin, ZHANG Hengjing, CHEN Fulong, et al. Spatiotemporal charging scheduling in wireless rechargeable sensor networks[J]. Computer Communications, 2020, 152: 155–170. doi: 10.1016/j.comcom.2020.01.037
[16]	LIU Tang, WU Baijun, ZHANG Shihao, et al. An effective multi-node charging scheme for wireless rechargeable sensor networks[C]. 2020 IEEE Conference on Computer Communications, Toronto, Canada, 2020: 2026–2035. doi: 10.1109/INFOCOM41043.2020.9155262.
[17]	ZHANG Fan, ZHANG Jie, and QIAN Yujie. A multi-node rechargeable algorithm via wireless charging vehicle with optimal traveling path in wireless rechargeable sensor networks[C]. The 10th International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 2018: 531–536. doi: 10.1109/ICUFN.2018.8437035.
[18]	吕增威, 魏振春, 韩江洪, 等. 基于多目标优化的无线传感器网络移动充电及数据收集算法[J]. 电子与信息学报, 2019, 41(8): 1877–1884. doi: 10.11999/JEIT180897 LV Zengwei, WEI Zhenchun, HAN Jianghong, et al. A mobile charging and data collecting algorithm based on multi-objective optimization[J]. Journal of Electronics &Information Technology, 2019, 41(8): 1877–1884. doi: 10.11999/JEIT180897
[19]	HE Shibo, CHEN Jiming, JIANG Fachang, et al. Energy provisioning in wireless rechargeable sensor networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(10): 1931–1942. doi: 10.1109/TMC.2012.161
[20]	WANG Cong, LI Ji, YE Fan, et al. A mobile data gathering framework for wireless rechargeable sensor networks with vehicle movement costs and capacity constraints[J]. IEEE Transactions on Computers, 2016, 65(8): 2411–2427. doi: 10.1109/TC.2015.2490060
[21]	IRWIN J D and NELMS R M. Basic Engineering Circuit Analysis[M]. Hoboken: John Wiley & Sons Inc, 2005.