Cloud-Assisted Ciphertext Policy Attribute Based Eencryption Data Sharing Encryption Scheme Based on BlockChain
-
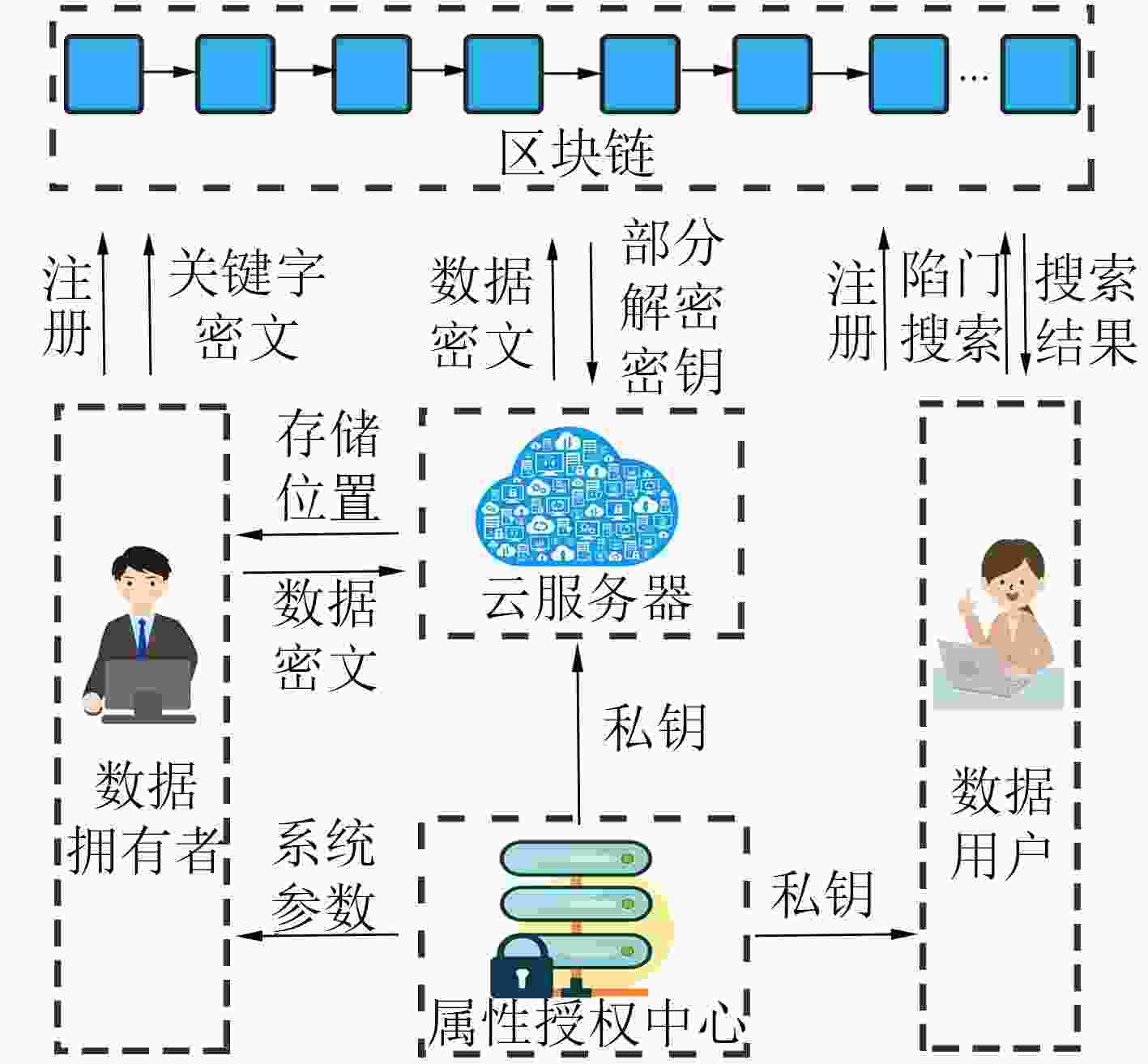
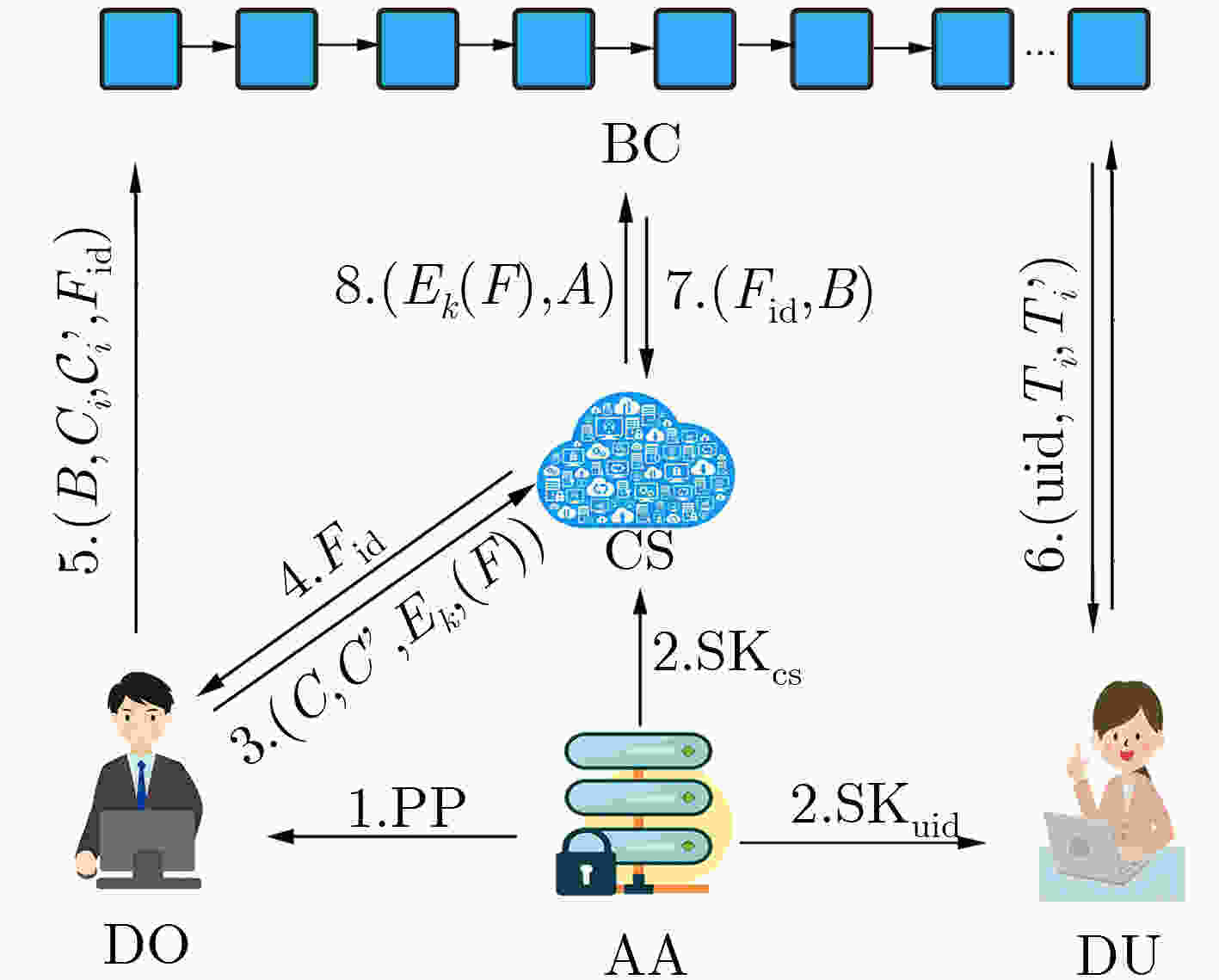
摘要: 针对云存储的集中化带来的数据安全和隐私保护问题,该文提出一种区块链上基于云辅助的密文策略属性基(CP-ABE)数据共享加密方案。该方案采用基于属性加密技术对加密数据文件的对称密钥进行加密,并上传到云服务器,实现了数据安全以及细粒度访问控制;采用可搜索加密技术对关键字进行加密,并将关键字密文上传到区块链(BC)中,由区块链进行关键字搜索保证了关键字密文的安全,有效地解决现有的云存储共享系统所存在的安全问题。该方案能够满足选择明文攻击下的不可区分性、陷门不可区分性和抗串联性。最后,通过性能评估,验证了该方案的有效性。Abstract: To solve the problem of data security and privacy preservation brought by the centralization of cloud storage, a cloud-assisted Ciphertext Policy Attribute Based Eencryption(CP-ABE) data sharing encryption scheme based on BlockChain(BC) is proposed. In this scheme, the symmetric key of the encrypted file is encrypted by attribute-based encryption and the encrypted file is uploaded to cloud server for realizing the data security and fine-grained access control. Searchable encryption technology is adopted to encrypt the keyword, and the keyword ciphertext is uploaded to the BlockChain. Keyword search is executed by the BlockChain to ensure the security of keyword ciphertext, which effectively solves the security problems existing in the cloud storage and sharing system. This scheme can satisfy the indiscernibility, trap indiscernibility and series resistance under the selective plaintext attack. Finally, the effectiveness of the scheme is verified by performance evaluation.
-
表 1 区块数据结构
Block Head Payload Block ID Block size Pre-block hash Timestamp Block producer ID Block producer signature Transaction ID size hash t Data Owner $\delta $ TX 表 2 效率分析
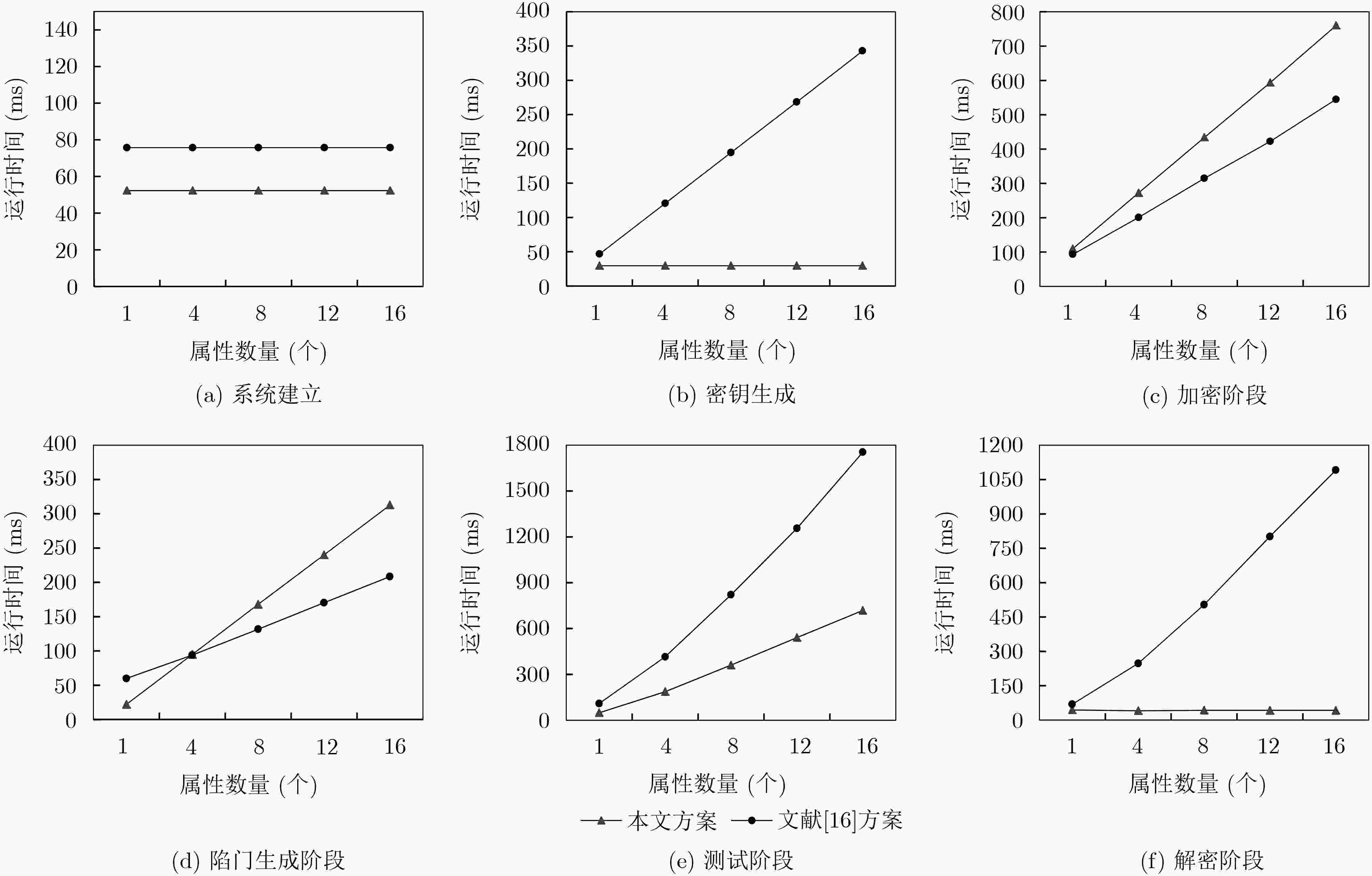
文献[15]方案 文献[16]方案 本文方案 Setup ${T_{\rm{P}}} + 3{T_{\rm{E}}}$ ${T_{\rm{P}}} + 4{T_{\rm{E}}} + {T_{\rm{M}}}$ ${T_{\rm{P}}} + 3{T_{\rm{E}}}$ KeyGen $4{T_{\rm{E}}} + 3{T_{\rm{M}}}$ $(2 + {n_{\rm{S}}}){T_{\rm{E}}} + (2 + {n_{\rm{S}}}){T_{\rm{M}}}$ $3{T_{\rm{E}}} + 2{T_{\rm{M}}}$ Encryption $\begin{aligned} & 2{T_{\rm{P} } } + (3{n_{\rm{U} } } + 5){T_{\rm{E} } } + (2{n_{\rm{U} } } + 2){T_{\rm{M} } }\\& {\rm{ + } }(2 + {n_{\rm{U} } }){T_{\rm{H} } }\end{aligned}$ ${T_{\rm{P}}} + (4{n_{\rm{U}}} + 6){T_{\rm{E}}} + (4{n_{\rm{U}}} + 8){T_{\rm{M}}}{\rm{ + }}{T_{\rm{H}}}$ $\begin{aligned} & 2{T_{\rm{P} } } + (2{n_{\rm{U} } } + 3){T_{\rm{E} } } + ({n_{\rm{U} } } + 3){T_{\rm{M} } }\\& {\rm{ + } }(1 + {n_{\rm{U} } }){T_{\rm{H} } }\end{aligned}$ Trapdoor ${T_{\rm{E}}} + {T_{\rm{H}}}$ $({n_{\rm{S}}} + 5){T_{\rm{E}}} + 3{T_{\rm{M}}} + {T_{\rm{H}}}$ $(2{n_{\rm{S}}} + 1){T_{\rm{E}}} + {n_{\rm{S}}}{T_{\rm{M}}} + (1 + {n_{\rm{S}}}){T_{\rm{H}}}$ Test ${T_{\rm{P}}} + {T_{\rm{E}}} + {T_{\rm{H}}}$ $(2{n_{\rm{S}}} + 3){T_{\rm{P}}} + {n_{\rm{S}}}{T_{\rm{E}}} + (2{n_{\rm{S}}} + 1){T_{\rm{M}}}$ $2{n_{\rm{S}}}{T_{\rm{P}}} + (2{n_{\rm{S}}} - 2){T_{\rm{E}}} + (2{n_{\rm{S}}} - 1){T_{\rm{M}}}$ Decryption $(2 + 2{n_{\rm{S}}}){T_{\rm{P}}} + 2{n_{\rm{S}}}{T_{\rm{E}}} + (2{n_{\rm{S}}} + 3){T_{\rm{M}}}$ $(2{n_{\rm{S}}} + 1){T_{\rm{P}}} + {n_{\rm{S}}}{T_{\rm{E}}} + (2{n_{\rm{S}}} + 1){T_{\rm{M}}}$ $3{T_{\rm{P}}} + 2{T_{\rm{E}}} + 4{T_{\rm{M}}}$ -
[1] 牛淑芬, 王金风, 王伯彬, 等. 区块链上基于B+树索引结构的密文排序搜索方案[J]. 电子与信息学报, 2019, 41(10): 2409–2415. doi: 10.11999/JEIT190038NIU Shufen, WANG Jinfeng, WANG Bobin, et al. Ciphertext sorting search scheme based on B+ tree index structure on blockchain[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2409–2415. doi: 10.11999/JEIT190038 [2] 黄穗, 陈丽炜, 范冰冰. 基于CP-ABE和区块链的数据安全共享方法[J]. 计算机系统应用, 2019, 28(11): 79–86. doi: 10.15888/j.cnki.csa.007144HUANG Sui, CHEN Liwei, and FAN Bingbing. Data security sharing method based on CP-ABE and blockchain[J]. Computer Systems and Applications, 2019, 28(11): 79–86. doi: 10.15888/j.cnki.csa.007144 [3] 牛淑芬, 谢亚亚, 杨平平, 等. 加密邮件系统中基于身份的可搜索加密方案[J]. 电子与信息学报, 2020, 42(7): 1803–1810. doi: 10.11999/JEIT190578NIU Shufen, XIE Yaya, YANG Pingping, et al. Identity-based searchable encryption scheme for encrypted email system[J]. Journal of Electronics &Information Technology, 2020, 42(7): 1803–1810. doi: 10.11999/JEIT190578 [4] SAHAI A and WATERS B. Fuzzy identity-based encryption[C]. The 24th annual international conference on Theory and Applications of Cryptographic Techniques, Berlin Germany, 2005. doi: 10.1007/11426639_27. [5] 张玉磊, 文龙, 王浩浩, 等. 多用户环境下无证书认证可搜索加密方案[J]. 电子与信息学报, 2020, 42(5): 1094–1101. doi: 10.11999/JEIT190437ZHANG Yulei, WEN Long, WANG Haohao, et al. Certificateless authentication searchable encryption scheme for multi-user[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1094–1101. doi: 10.11999/JEIT190437 [6] SONG D X, WAGNER D, and PERRIG A. Practical techniques for searches on encrypted data[C]. 2020 IEEE Symposium on Security and Privacy. S&P 2000, Berkeley, USA, 2000. doi: 10.1109/SECPRI.2000.848445. [7] BONEH D, CRESCENZO G D, OSTROVSKY R, et al. Public key encryption with keyword search[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 506–522. doi: 10.1007/978-3-540-24676-3_30. [8] WANG Yong, ZHANG Aiqing, ZHANG Peiyun, et al. Cloud-assisted EHR sharing with security and privacy preservation via consortium Blockchain[J]. IEEE Access, 2019, 7: 136704–136719. doi: 10.1109/ACCESS.2019.2943153 [9] NAKAMOTO S. Bitcoin: A peer-to-peer electronic cash system[EB/OL]. https://bitcoin.org/en/bitcoin-paper, 2016. [10] ZHENG Zibin, XIE Shaoan, DAI Hongning, et al. An overview of Blockchain technology: Architecture, consensus, and future trends[C]. 2017 IEEE International Congress on Big Data, Honolulu, USA, 2017. doi: 10.1109/BigDataCongress.2017.85. [11] ZHENG Dong, WU Axin, and ZHANG Yinghui. Efficient and privacy-preserving medical data sharing in internet of things with limited computing power[J]. IEEE Access, 2018, 6: 28019–28027. doi: 10.1109/ACCESS.2018.2840504 [12] 张良嵩. 基于拜占庭容错的区块链共识算法研究[D]. [硕士论文], 电子科技大学, 2020.ZHANG Liangsong. Research of blockchain consensus algorithm based on byzantine fault tolerance[D]. [Master dissertation], University of Electronic Science and Technology of China, 2020. [13] 刘格昌, 李强. 基于可搜索加密的区块链数据隐私保护机制[J]. 计算机应用, 2019, 39(S2): 140–146.LIU Gechang and LI Qiang. BlockChain data privacy protection mechanism based on searchable encryption[J]. Journal of Computer Applications, 2019, 39(S2): 140–146. [14] 齐芳, 李艳梅, 汤哲. 可撤销和可追踪的密钥策略属性基加密方案[J]. 通信学报, 2018, 39(11): 63–69. doi: 10.11959/j.issn.1000-436x.2018231QI Fang, LI Yanmei, and TANG Zhe. Revocable and traceable key-policy attribute-based encryption scheme[J]. Journal on Communications, 2018, 39(11): 63–69. doi: 10.11959/j.issn.1000-436x.2018231 [15] WANG Shangping, ZHANG Duo, ZHANG Yaling, et al. Efficiently revocable and searchable attribute-based encryption scheme for mobile cloud storage[J]. IEEE Access, 2018, 6: 30444–30457. doi: 10.1109/ACCESS.2018.2846037 [16] 胡媛媛, 陈燕俐, 朱敏惠. 可实现隐私保护的基于属性密文可搜索方案[J]. 计算机应用研究, 2019, 36(4): 1158–1164. doi: 10.19734/j.issn.1001-3695.2017.12.0760HU Yuanyuan, CHEN Yanli, and ZHU Minhui. Privacy protection attribute-based ciphertext search scheme[J]. Application Research of Computers, 2019, 36(4): 1158–1164. doi: 10.19734/j.issn.1001-3695.2017.12.0760 [17] The pairing-based cryptography library[EB/OL]. http://crypto.stanford.edu/pbc/, 2015. -





 下载:
下载:


 下载:
下载:
