基于混沌的双模块Feistel结构高安全性高速分组密码算法安全性分析

杜小妮; 段娥娥; 王天心

doi:10.11999/JEIT200057

基于混沌的双模块Feistel结构高安全性高速分组密码算法安全性分析

doi: 10.11999/JEIT200057

西北师范大学数学与统计学院兰州 730070

基金项目: 国家自然科学基金(61772022)

详细信息

作者简介:
杜小妮：女，1972年生，教授，博士生导师，研究方向为密码学与信息安全

段娥娥：女，1996年生，硕士生，研究方向为密码学与信息安全

王天心：女，1997年生，硕士生，研究方向为密码学与信息安全

通讯作者:
段娥娥　eeduan@126.com

中图分类号: TN918.4
计量
- 文章访问数: 1192
- HTML全文浏览量: 328
- PDF下载量: 79
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-14
- 修回日期: 2020-11-23
- 网络出版日期: 2020-12-03
- 刊出日期: 2021-05-18

Security Analysis of Block Cipher CFE

College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China

Funds: The National Natural Science Foundation of China (61772022)

摘要

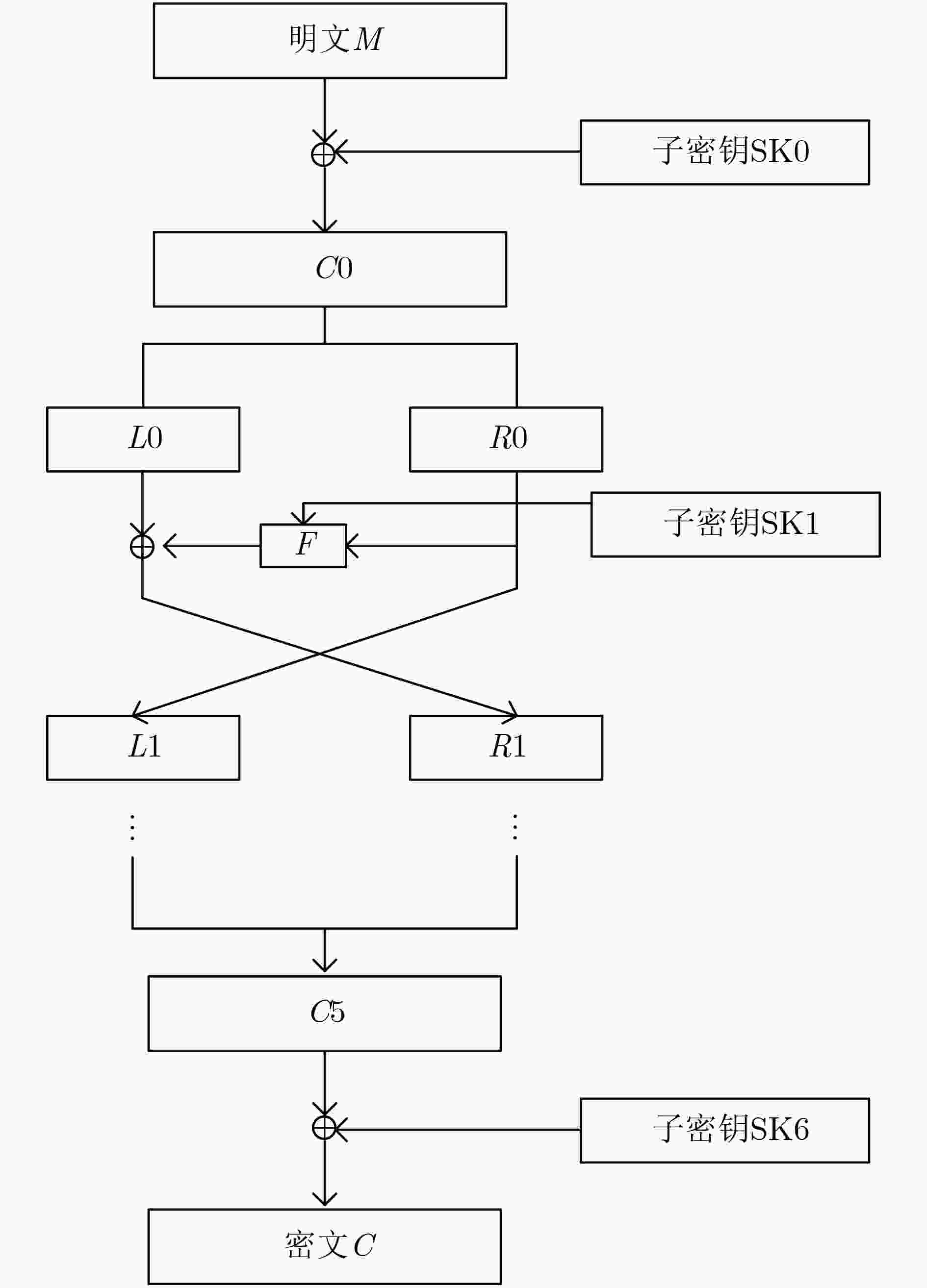
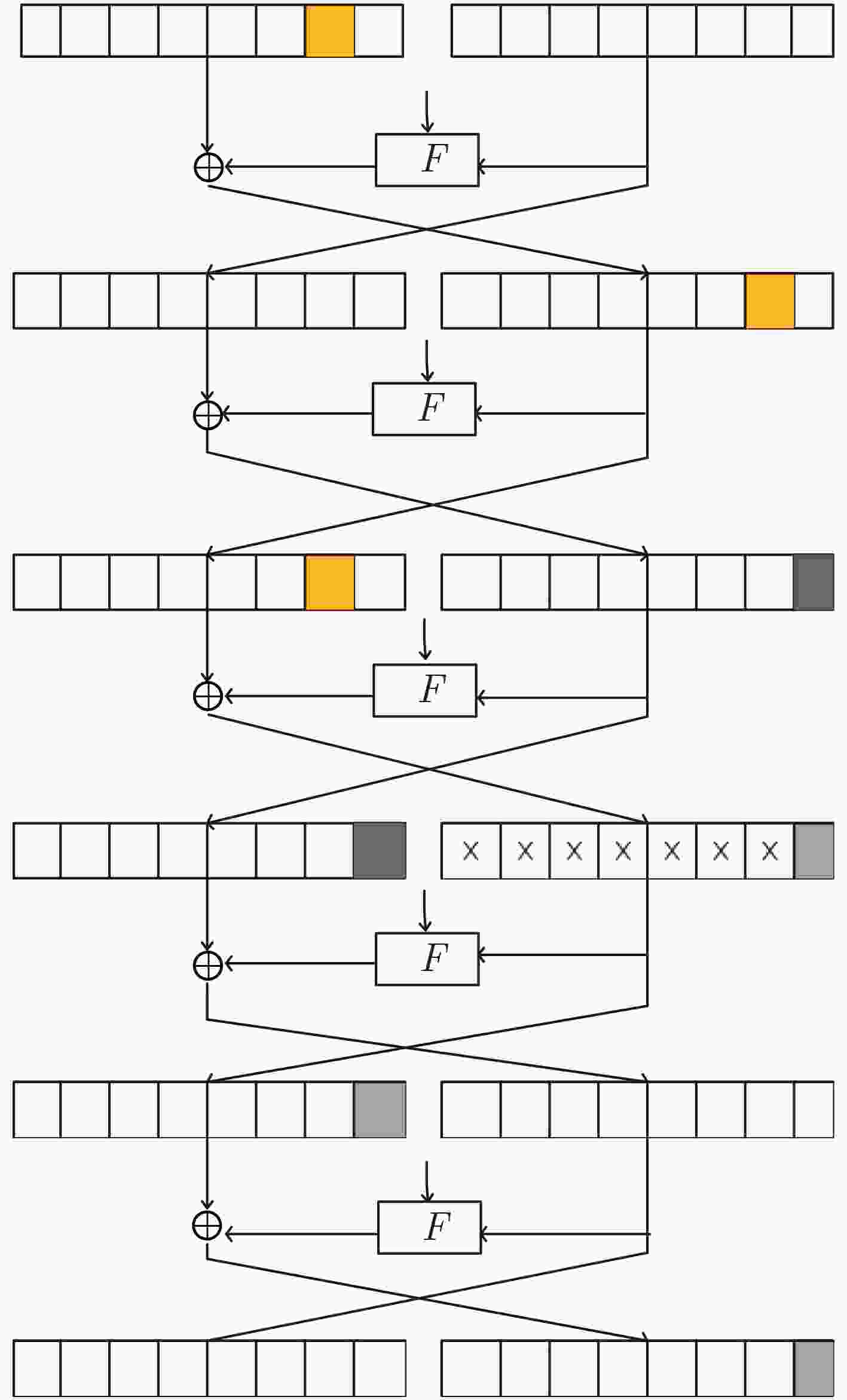
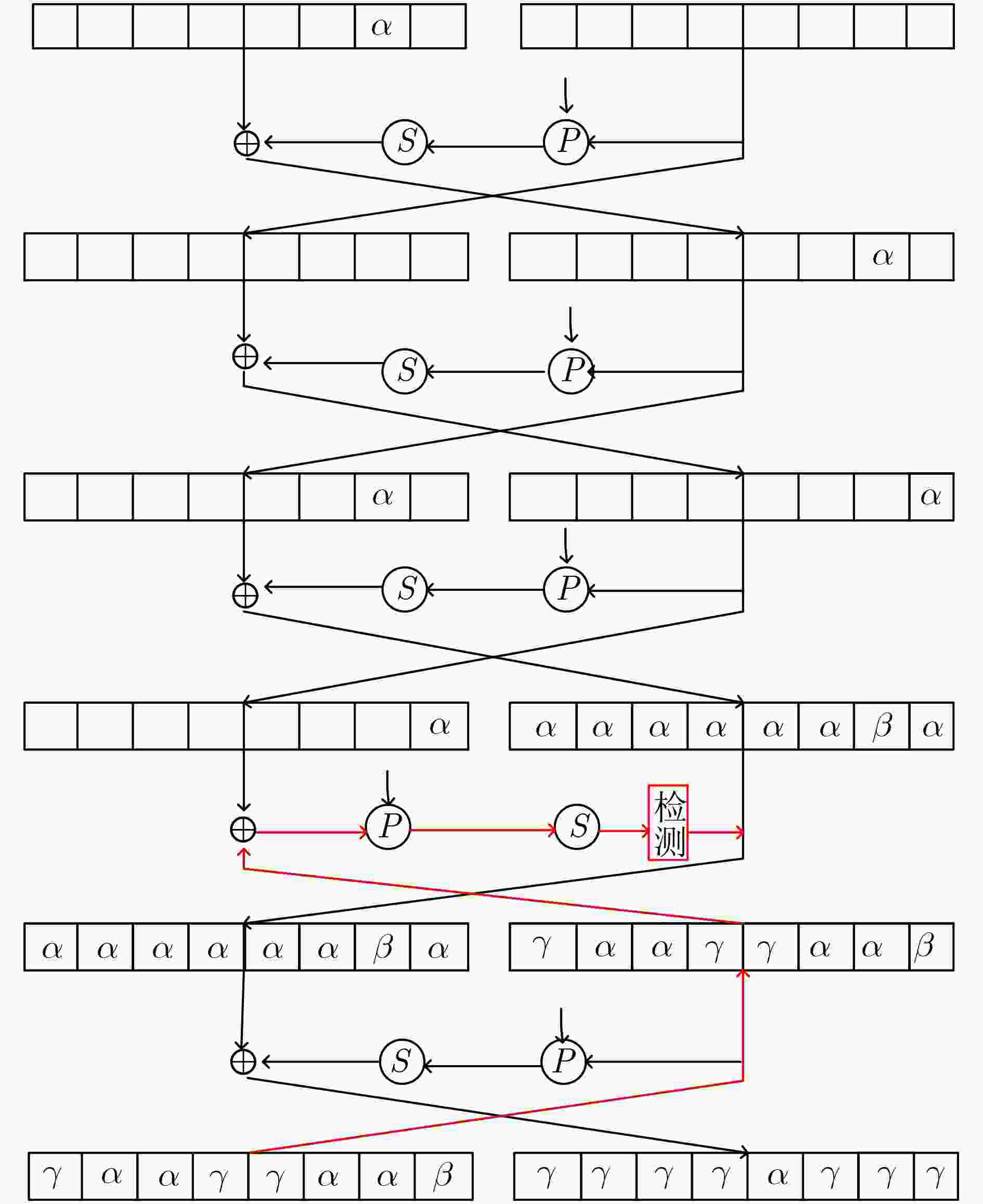
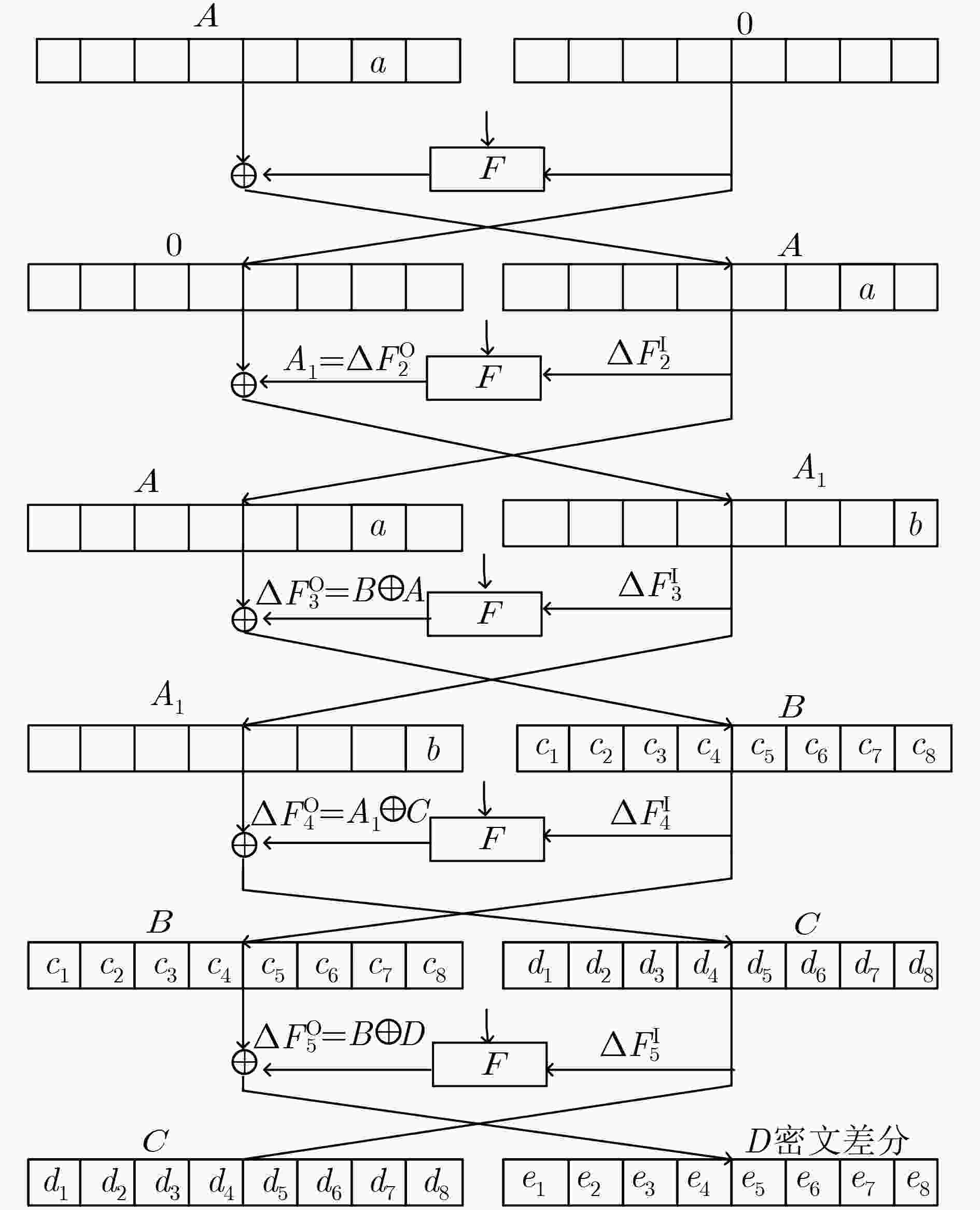
摘要: 该文对基于混沌的双模块Feistel结构(CFE)高安全性高速分组算法的安全性进行了分析。分析结果表明，算法不适合用积分攻击、中间相遇攻击、不变量攻击、插值攻击和循环移位攻击分析其安全性；可以抵抗相关密钥攻击；更进一步地构造出了5轮不可能差分特征链，并利用其进行区分攻击；求得算法的活性S盒下界为6，概率约为2^–21；算法存在5轮零相关线性特征。
- 混沌密码 /
- 差分活性S盒 /
- 不可能差分攻击 /
- 区分攻击 /
- 零相关线性攻击
Abstract: The security of high security and high speed block cipher algorithm of two-module FEistel structure based on Chaos (CFE) is analyzed. The results show that the cipher is not suitable to use integral attack, meat-in-the-middle attack, invariant attack, interpolation attack and circle shift attack to analyze its security. And it can resist the related-key attack. Furthermore, 5 rounds of impossible differential characteristic are constructed and used to distinguish attacks. The lower bound of the active S-box is 6, and the probability is about 2^–21. There are 5 rounds of linear characteristic with zero-correlation.
- Chaos cipher /
- Differential active S-box /
- Impossible differential attack /
- Distinguish attack /
- Zero-correlation linear attack

HTML全文

图 1 结构图

下载: 全尺寸图片幻灯片

图 2 轮函数

下载: 全尺寸图片幻灯片

图 3 5轮不可能差分特征图

下载: 全尺寸图片幻灯片

图 4 5轮零相关线性区分器

下载: 全尺寸图片幻灯片

图 5 积分攻击

下载: 全尺寸图片幻灯片

图 6 5轮中间相遇区分器

下载: 全尺寸图片幻灯片

表 1 差分活性S盒个数下界

轮数 1 2 3 4 5

128/256 bit 0 2 3 5 6

下载: 导出CSV

参考文献(16)

[1]	BIHAM E and SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[J]. Journal of Cryptology, 1991, 4(1): 3–72. doi: 10.1007/BF00630563
[2]	杨伟伟, 刘光杰, 戴跃伟. 基于交叉耦合映像格子时空混沌的S盒设计[J]. 应用科学学报, 2015, 33(4): 438–448. doi: 10.3969/j.issn.0255-8297.2015.04.010 YANG Weiwei, LIU Guangjie, and DAI Yuewei. Design of S-boxes based on spatiotemporal chaotic systems of cross coupled map lattices[J]. Journal of Applied Sciences—Electronics and Information Engineering, 2015, 33(4): 438–448. doi: 10.3969/j.issn.0255-8297.2015.04.010
[3]	贾平, 徐洪, 戚文峰. 轻量S盒密码性质研究[J]. 密码学报, 2015, 2(6): 497–504. doi: 10.13868/j.cnki.jcr.000096 JIA Ping, XU Hong, and QI Wenfeng. Research on cryptographic properties of lightweight S-boxes[J]. Journal of Cryptologic Research, 2015, 2(6): 497–504. doi: 10.13868/j.cnki.jcr.000096
[4]	杨萍. 基于MILP方法的轻量级分组密码的安全性分析[D]. [硕士论文], 山东师范大学, 2018. YANG Ping. Security analysis of lightweight block cipher based on MILP method[D]. [Master dissertation], Shandong Normal University, 2018.
[5]	吴文玲, 张蕾. 不可能差分密码分析研究进展[J]. 系统科学与数学, 2008, 28(8): 971–983. WU Wenling and ZHANG Lei. The state-of-the-art of research on impossible differential cryptanalysis[J]. Journal of Systems Science and Mathematical Sciences, 2008, 28(8): 971–983.
[6]	韦永壮, 史佳利, 李灵琛. LiCi分组密码算法的不可能差分分析[J]. 电子与信息学报, 2019, 41(7): 1610–1617. doi: 10.11999/JEIT180729 WEI Yongzhuang, SHI Jiali, and LI Lingchen. Impossible differential cryptanalysis of LiCi block cipher[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1610–1617. doi: 10.11999/JEIT180729
[7]	张仕伟, 陈少真. SIMON不可能差分及零相关路径自动化搜索算法[J]. 软件学报, 2018, 29(11): 3544–3553. doi: 10.13328/j.cnki.jos.005296 ZHANG Shiwei and CHEN Shaozhen. Automatic search algorithm for impossible differential trials and zero-correlation linear trials in SIMON[J]. Journal of Software, 2018, 29(11): 3544–3553. doi: 10.13328/j.cnki.jos.005296
[8]	马楚焱, 刘国强, 李超. 对PICO和RECTANGLE的零相关线性分析[J]. 密码学报, 2017, 4(5): 413–422. doi: 10.13868/j.cnki.jcr.000193 MA Chuyan, LIU Guoqiang, and LI Chao. Zero-correlation linear cryptanalysis on PICO and RECTANGLE[J]. Journal of Cryptologic Research, 2017, 4(5): 413–422. doi: 10.13868/j.cnki.jcr.000193
[9]	DUO Lei, LI Chao, and FENG Keqin. Square like attack on camellia[C]. The International Conference on Information and Communications Security, Zhengzhou, China, 2007: 269–283. doi: 10.1007/978-3-540-77048-0_21.
[10]	任炯炯, 李航, 陈少真. 减轮Simeck算法的积分攻击[J]. 电子与信息学报, 2019, 41(9): 2156–2163. doi: 10.11999/JEIT180849 REN Jiongjiong, LI Hang, and CHEN Shaozhen. Integral attack on reduced-round simeck algorithm[J]. Journal of Electronics &Information Technology, 2019, 41(9): 2156–2163. doi: 10.11999/JEIT180849
[11]	邓元豪, 金晨辉, 赵杰卿. Type-3型广义Feistel结构的中间相遇攻击[J]. 密码学报, 2019, 6(1): 27–36. doi: 10.13868/j.cnki.jcr.000280 DENG Yuanhao, JIN Chenhui, and ZHAO Jieqing. Meet-in-the-middle attack on Type-3 Feistel structure[J]. Journal of Cryptologic Research, 2019, 6(1): 27–36. doi: 10.13868/j.cnki.jcr.000280
[12]	汪艳凤, 吴文玲. 分组密码TWINE的中间相遇攻击[J]. 软件学报, 2015, 26(10): 2684–2695. doi: 10.13328/j.cnki.jos.004805 WANG Yanfeng and WU Wenling. Meet-in-the-Middle attack on TWINE block cipher[J]. Journal of Software, 2015, 26(10): 2684–2695. doi: 10.13328/j.cnki.jos.004805
[13]	JAKOBSEN T and KNUDSEN L R. The interpolation attack on block ciphers[C]. The International Workshop on Fast Software Encryption, Haifa, Israel, 1997: 28–40. doi: 10.1007/BFb0052332.
[14]	金晨辉, 杨阳, 祁传达. 对混沌序列密码的相关密钥攻击[J]. 电子与信息学报, 2006, 28(3): 410–414. JIN Chenhui, YANG Yang, and QI Chuanda. A related-key attack on chaotic stream ciphers[J]. Journal of Electronics &Information Technology, 2006, 28(3): 410–414.
[15]	TODO Y, LEANDER G, and SASAKI Y. Nonlinear invariant attack: Practical attack on full SCREAM, iSCREAM, and Midori64[J]. Journal of Cryptology, 2019, 32(4): 1383–1422. doi: 10.1007/s00145-018-9285-0
[16]	XIE E Y, LI Chengqing YU Simin, et al. On the cryptanalysis of Fridrich’s chaotic image encryption scheme[J]. Signal Processing, 2017, 132: 150–154. doi: 10.1016/j.sigpro.2016.10.002