Consensus Analysis of the Second Order Multi-agent Systems Based on Large Communication Delay
-
摘要: 在有向网络拓扑下，该文研究了2阶大时滞多智能体系统的一致性，提出具有加权项的时滞状态导数反馈协议，改进了大通讯时滞导致系统震荡的问题。首先引入具有加权项的时滞状态导数反馈协议，并给出2阶多智能体系统的闭环形式；然后采用频域分析法求出2阶多智能体系统渐近实现稳态一致的充要条件，并证明与传统一致性协议相比，2阶多智能体系统在具有加权项的时滞状态导数反馈协议下能够容忍更大的通讯时滞；最后通过数值仿真验证了具有加权项的时滞状态导数反馈协议的优势。Abstract: Under the directed network topology, the consensus of the second order multi-agent system with large communication delay is studied, the protocol of delayed-state-derivative feedback with weighting term is proposed, which improves the problem of system oscillation caused by large communication delay. Firstly, the delayed-state-derivative feedback protocol with weighting term is introduced, and the closed-loop form of the second-order multi-agent system is given. Then, the sufficient and necessary conditions for the asymptotic steady-state consensus of the second-order multi-agent system are obtained by using the frequency domain analysis method, and it is proved that the second-order multi-agent system can tolerate the greater communication delay under the delayed-state-derivative feedback protocol with weighting term. Finally, the advantage of the delayed-state-derivative feedback protocol with weighting term is verified by numerical simulation.
-
Key words:
- Multi-agent system /
- Consensus /
- Robustness /
- Communication delay
-
图 1 在
$ \beta {\rm{ = }}0$ ,$ {r_1}{\rm{ = }}{r_2}{\rm{ = }}1$ 且$ \tau {\rm{ = }}1.3$ 下系统的状态
图 2 在
$\beta {\rm{ = }}0.2$ ,${r_1}{\rm{ = }}{r_2}{\rm{ = }}1$ 且$\tau {\rm{ = }}1.35$ 下系统的状态 -
余莹莹. 多智能体系统一致性若干问题的研究[D]. [博士论文], 华中科技大学, 2010: 3–26.YU Yingying. Research on several problems of consensus in multi-agent systems[D]. [Ph. D. dissertation], Huazhong University of Science and Technology, 2010: 3–26. OLFATI-SABER R and MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520–1533. doi: 10.1109/TAC.2004.834113 DEGROOT M H. Reaching a consensus[J]. Journal of the American Statistical Association, 1974, 69(345): 118–121. doi: 10.2307/2285509 VICSEK T, CZIRÓK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 75(6): 1226–1229. doi: 10.1103/PhysRevLett.75.1226 JADBABAIE A, LIN Jie, and MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988–1001. doi: 10.1109/tac.2003.812781 蒋国平, 周映江. 基于收敛速率的多智能体系统一致性研究综述[J]. 南京邮电大学学报: 自然科学版, 2017, 37(3): 15–25. doi: 10.14132/j.cnki.1673-5439.2017.03.002JIANG Guoping and ZHOU Yingjiang. Research on consensus of multi-agent systems based on convergence rate[J]. Journal of Nanjing University of Posts and Telecommunications:Natural Science Edition, 2017, 37(3): 15–25. doi: 10.14132/j.cnki.1673-5439.2017.03.002 高杨, 李东生, 程泽新. 无人机分布式集群态势感知模型研究[J]. 电子与信息学报, 2018, 40(6): 1271–1278. doi: 10.11999/JEIT170877GAO Yang, LI Dongsheng, and CHENG Zexin. UAV distributed swarm situation awareness model[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1271–1278. doi: 10.11999/JEIT170877 张岩, 孙世宇, 胡永江, 等. 基于特征距离与内点的随机抽样一致性算法[J]. 电子与信息学报, 2018, 40(4): 928–935. doi: 10.11999/JEIT170703ZHANG Yan, SUN Shiyu, HU Yongjiang, et al. Random sample consensus algorithm based on feature distance and inliers[J]. Journal of Electronics &Information Technology, 2018, 40(4): 928–935. doi: 10.11999/JEIT170703 YU Wenwu, CHEN Guanrong, and GAO Ming. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems[J]. Automatica, 2010, 46(6): 1089–1095. doi: 10.1016/j.automatica.2010.03.006 REN Wei and ATKINS E. Distributed multi-vehicle coordinated control via local information exchange[J]. International Journal of Robust and Nonlinear Control, 2007, 17(10/11): 1002–1033. doi: 10.1002/rnc.1147 ZOU Wencheng, SHI Peng, XIANG Zhengrong, et al. Finite-time consensus of second-order switched nonlinear multi-agent systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(5): 1757–1762. doi: 10.1109/TNNLS.2019.2920880 REN Hongwei and DENG Feiqi. Stochastic bounded consensus of second-order multi-agent systems in noisy environment[J]. Chinese Physics B, 2017, 26(10): 100506. doi: 10.1088/1674-1056/26/10/100506 ZHENG Yuanshi, ZHAO Qi, MA Jingjing, et al. Second-order consensus of hybrid multi-agent systems[J]. Systems & Control Letters, 2019, 125: 51–58. doi: 10.1016/j.sysconle.2019.01.009 LIU Chenglin and TIAN Yuping. Coordination of multi-agent systems with communication delays[J]. IFAC Proceedings Volumes, 2008, 41(2): 10782–10787. doi: 10.3182/20080706-5-KR-1001.01828 WU Zhihai and FANG Huajing. Improvement for consensus performance of multi-agent systems based on delayed-state-derivative feedback[J]. Journal of Systems Engineering and Electronics, 2012, 23(1): 137–144. doi: 10.1109/JSEE.2012.00017 WU Zhihai and FANG Huajing. Delayed-state-derivative feedback for improving consensus performance of second-order delayed multi-agent systems[J]. International Journal of Systems Science, 2012, 43(1): 140–152. doi: 10.1080/00207721003802289 王娜, 王健, 曹智明, 等. 加权平均预测的一阶多智能体系统一致性的采样控制[J]. 空军工程大学学报: 自然科学版, 2017, 18(1): 105–110. doi: 10.3969/j.issn.1009-3516.2017.01.018WANG Na, WANG Jian, and CAO Zhiming, et al. Sampled-data consensus of first-order multi-agent systems with weighted average prediction[J]. Journal of Air Force Engineering University:Natural Science Edition, 2017, 18(1): 105–110. doi: 10.3969/j.issn.1009-3516.2017.01.018 WU Zhihai, FANG Huajing, and SHE Yingying. Weighted average prediction for improving consensus performance of second-order delayed multi-agent systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) , 2012, 42(5): 1501–1508. doi: 10.1109/TSMCB.2012.2189384 -
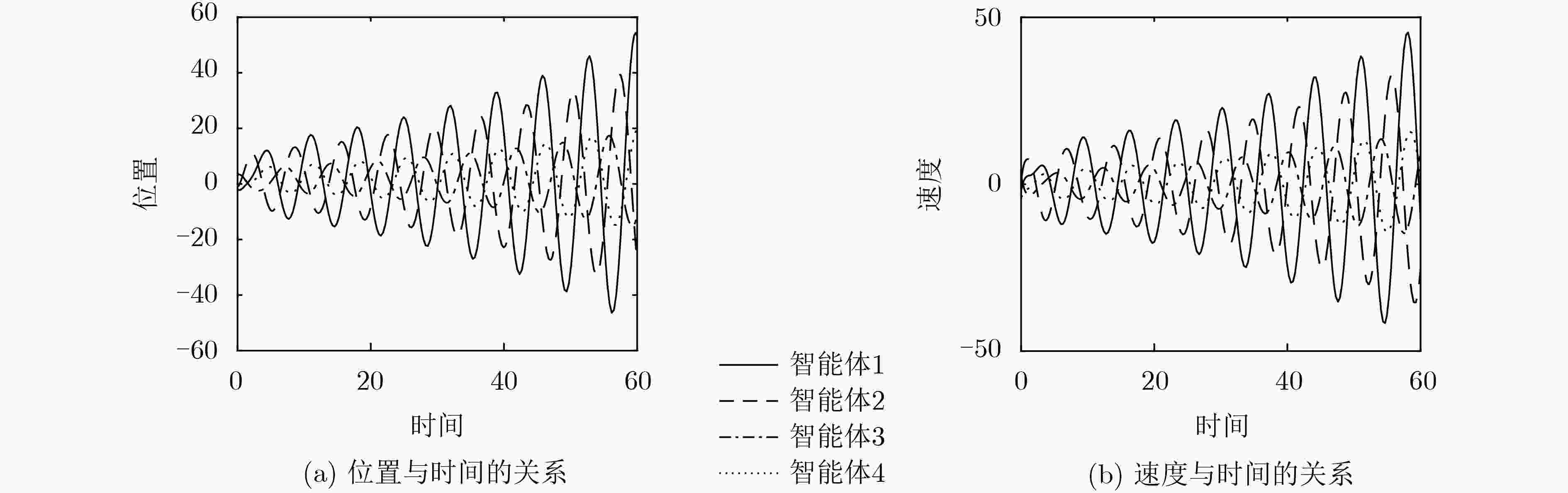
下载:
图(3)
计量
- 文章访问数: 1703
- HTML全文浏览量: 598
- PDF下载量: 52
- 被引次数: 0
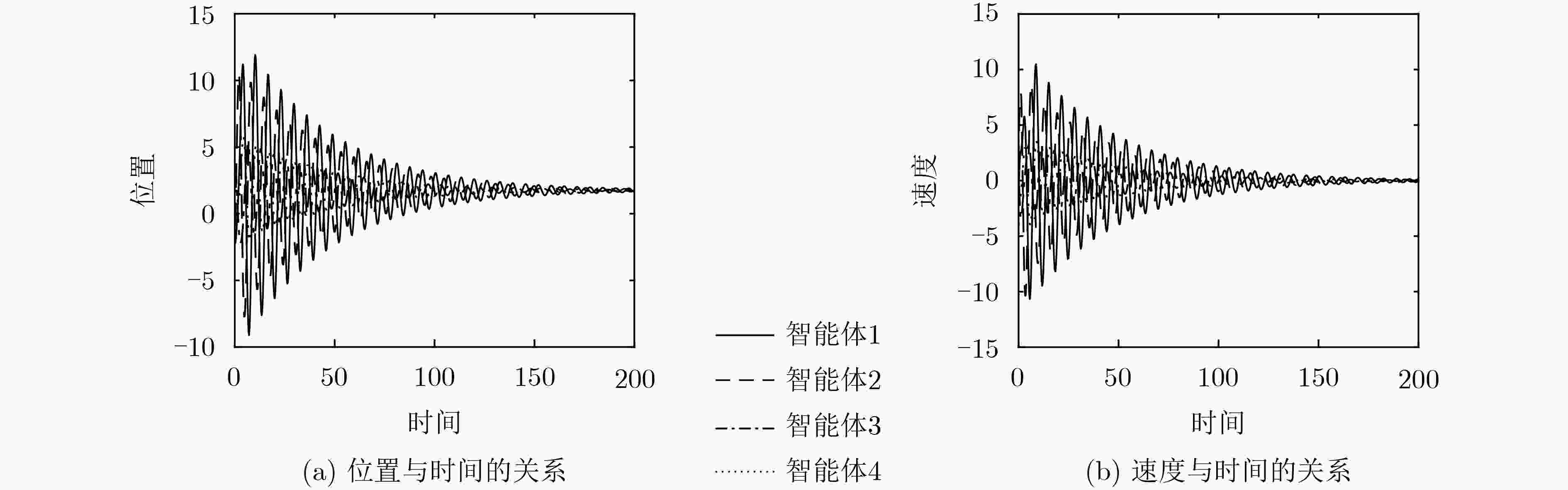
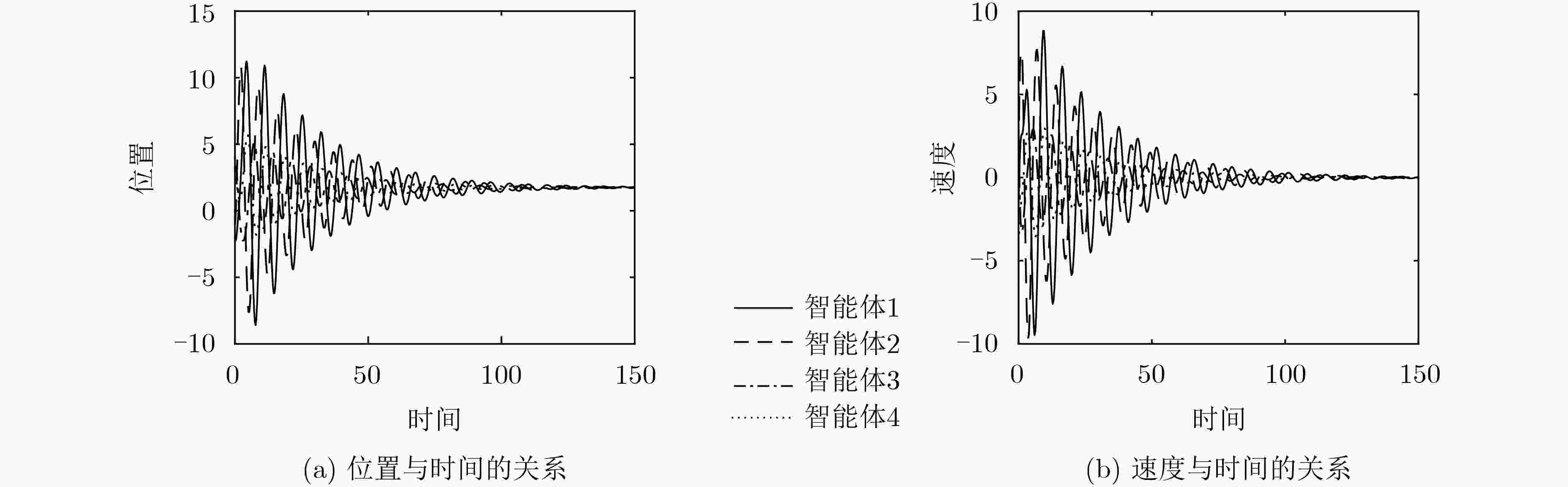
下载:
