Two Low-complexity Symbol Flipping Decoding Algorithms for Non-binary LDPC Codes
-
摘要: 该文提出两种低复杂度的基于符号翻转的多元低密度奇偶校验码(LDPC)译码算法:改进型多元加权译码算法(Iwtd-AlgB)和基于截断型预测机制的符号翻转(TD-SFDP)算法。Iwtd-AlgB算法利用外信息频率和距离系数的简单求和取代了迭代过程中的乘性运算操作;TD-SFDP算法结合外信息频率和翻转函数特性,对译码节点和有限域符号进行截断与划分,使得只有满足条件的节点和符号参与运算与翻转预测。仿真和数值结果显示,该文提出的两种算法在性能损失可控的前提下,可减少每次迭代的运算操作数,实现性能和复杂度之间的折中。Abstract: Two low-complexity symbol flipping decoding algorithms, the Improved weighted-Algorithm B algorithm (Iwtd-AlgB) and the Truncation-based Distance-Symbol-Flipping-Decoding with Prediction (TD-SFDP) algorithm, are presented for non-binary Low Density Parity Check (LDPC) codes. For the Iwtd-AlgB algorithm, the scaling factor of the flipping metric can be replaced by the simple sums of the extrinsic information and the distance-based parameter, which can avoid the multiplication operations in the iterations and thus can reduce the decoding complexity. For the presented TD-SFDP algorithm, the variable nodes and the finite field symbols are truncated and classified based on the extrinsic information frequency and the flipping function. Only those nodes/symbols that satisfy the designed conditions can be involved in the message updating process. Simulations and numeric results show that, the presented two decoding algorithms can reduce the computational complexity at each iteration with a controllable performance degradation, thus can make efficient trade-offs between performance and complexity.
-
表 1 Iwtd-AlgB算法
初始化:令迭代次数$k = 0$,最大迭代次数为${I_{\max }}$,设置门限值
$T$和汉明距离系${\theta _{d\left(z_j^{(k)},\;\sigma _{i,j}^{(k)}\right)} }$;译码迭代:当$k < {I_{\max }}$时,执行以下步骤 步骤 1:计算硬判决序列${\underline {{z} } ^{(k)} } = \left(z_0^{(k)},z_1^{(k)}, ··· ,z_{n - 1}^{(k)}\right)$; 步骤 2:计算伴随式${\underline {{s}} ^{(k)}}$,如果${\underline {{s} } ^{(k)} } = {\underline {{z} } ^{(k)} }{ {{H} }^{\rm{T} } } = \underline {{{\textit{0}}} }$,所有校
验方程满足,退出迭代;步骤 3:对$0 \le j \le n - 1$和$i \in {M_j}$,统计$n\left(\sigma _{i,j}^{(k)}\right)$,计算
$d\left(z_j^{(k)},\sigma _{i,j}^{(k)}\right)$,根据汉明距离选择确定系数${\theta _{d\left(z_j^{(k)},\sigma _{i,j}^{(k)}\right)} }$,根
据式(5)更新得到${z^{(k + 1)}}$;步骤 4:执行$k \leftarrow k + 1$; 输出:迭代译码结束,最终译码输出为
$\;\;\;\;{\underline {{z} } ^{(k)} } = \left(z_0^{(k)},z_1^{(k)}, ··· ,z_{n - 1}^{(k)}\right)$。表 3 译码算法每次迭代的计算复杂度比较
算法 每次迭代的运算操作数量 IM//RM GA GM IA//RA IC//RC wBRB $\delta $ $2\delta - m$ $2\delta $ $2\delta r$ $\delta (2r + 1) - 3m$ wtd-AlgB $\delta $ $3\delta - m$ $2\delta $ $\delta $ $\delta $ Iwtd-AlgB 0 $3\delta - m$ $2\delta $ $2\delta $ $\delta $ P-SFDP 0 ${\rm{2}}\gamma (\rho - 1)$ $\gamma (2\rho {\rm{ - }}1)$ $(\gamma \rho - \gamma + 1) \\ \times (\gamma r + 3\gamma + 5r + 1)$ $(\gamma + r - 1) \times (\gamma \rho - \gamma + 1) \\+ 2(n - 1)$ D-SFDP 0 $(\gamma \rho - \gamma + 1) \\ \times \gamma (\gamma + r) + 2\gamma (\rho - 1)$ $\gamma (2\rho {\rm{ - }}1)$ $(\gamma \rho - \gamma + 1) \\ \times ({\gamma ^2} + 2\gamma r + 4r + 2\gamma )$ $(\gamma + r - 1) \times (\gamma \rho - \gamma + 1) \\+ 2(n - 1)$ TD-SFDP 0 ${n_{{T_1}}}\gamma {n_{{T_2}}} + 2\gamma (\rho - 1)$ $\gamma (2\rho {\rm{ - }}1)$ ${n_{ {T_1} } }{n_{ {T_2} } }(r + \gamma + 1) \\ + {n_{ {T_1} } }(r{\rm{ + } }\gamma ) + n\gamma$ ${n_{ {T_1} } }({n_{ {T_2} } } + \gamma - 2) \\ + 2({n_{ {T_1} } } - 1)$ 备注:IM: 整数乘法;RM: 实数乘法;GA:有限域加法;GM:有限域乘法;IA:整数加法;RA:实数加法;IC:整数比较;RC:实数比较。 表 2 TD-SFDP算法
初始化:令迭代次数$k = 0$,最大迭代次数为${I_{\max }}$,设置门限值
${T_1}$和${T_2}$以及汉明距离系数${\theta _{d\left(z_j^{(k)},\sigma _{i,j}^{(k)}\right)} }$;译码迭代:当$k < {I_{\max }}$时,执行以下步骤 步骤 1:计算硬判决序列${\underline {{z} } ^{(k)} } = \left(z_0^{(k)},z_1^{(k)}, ··· ,z_{n - 1}^{(k)}\right)$; 步骤 2:计算伴随式${\underline {{s}} ^{(k)}}$,如果${\underline {{s}} ^{(k)}} = {\underline {{z}} ^{(k)}}{{{H}}^{\rm{T}}} = \underline {{0}} $,所有校
验方程满足,退出迭代;步骤 3:计算外信息频率$n(\sigma _{i,j}^{(k)})$,确定截断集合${{{J}}^{(k)}}$和${{S}}_j^{\left( k \right)}$,
计算$\Delta E_j^{(k)}\left(z_j^{ * (k)},z_j^{(k)}\right)$, $\Delta E_{\max \_j}^{(k)}$, $\Delta E_{\max \_{p^{(k)}}}^{(k)}$, ${p^{(k)}}$以及
$v_{{p^{\left( k \right)}}}^{\left( k \right)}$;步骤 4:执行$k \leftarrow k + 1$; 输出:迭代译码结束,最终译码输出为
$\;\;\;\;{\underline {{z} } ^{(k)} } = \left(z_0^{(k)},z_1^{(k)}, ··· ,z_{n - 1}^{(k)}\right)$。表 4
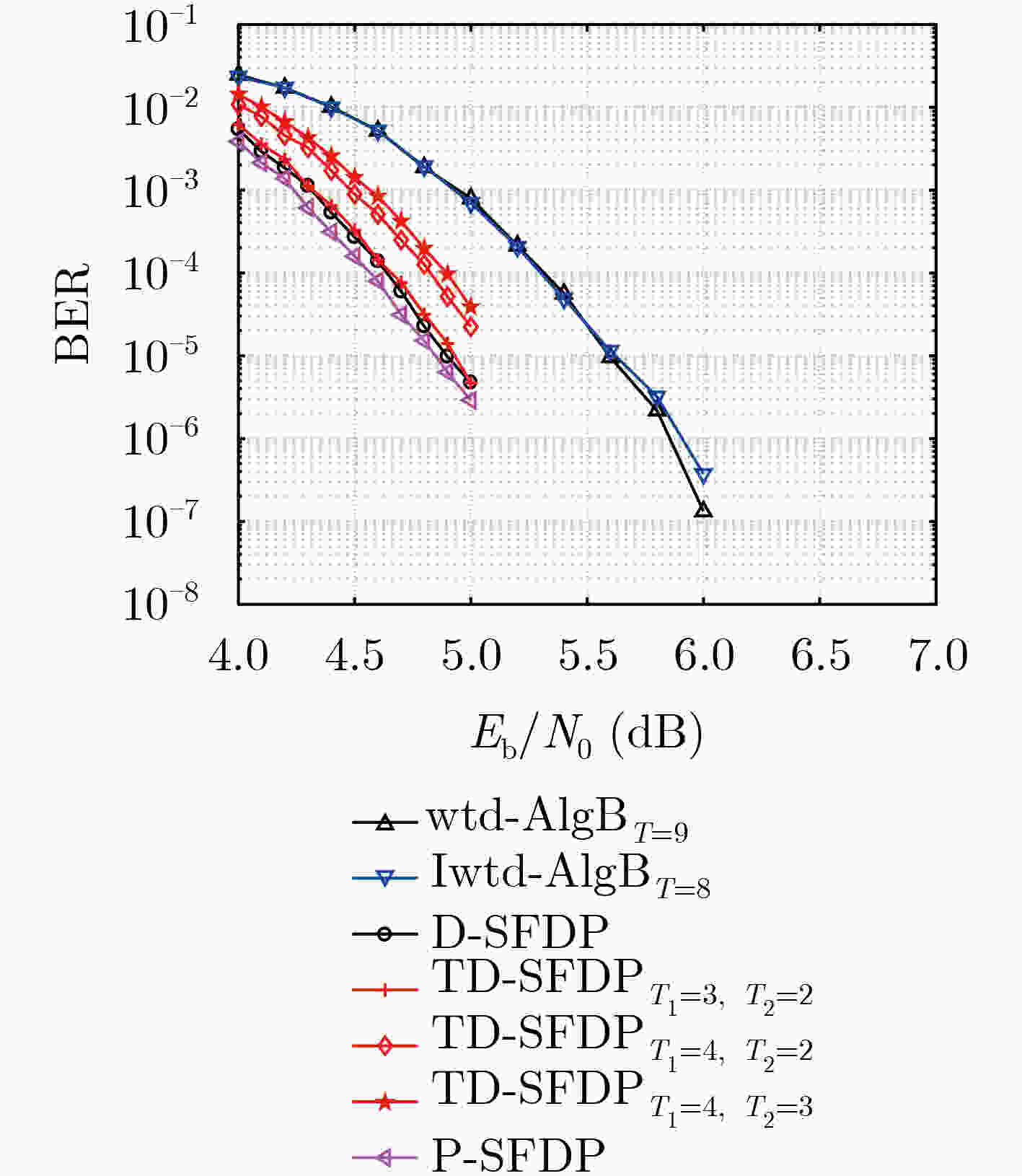
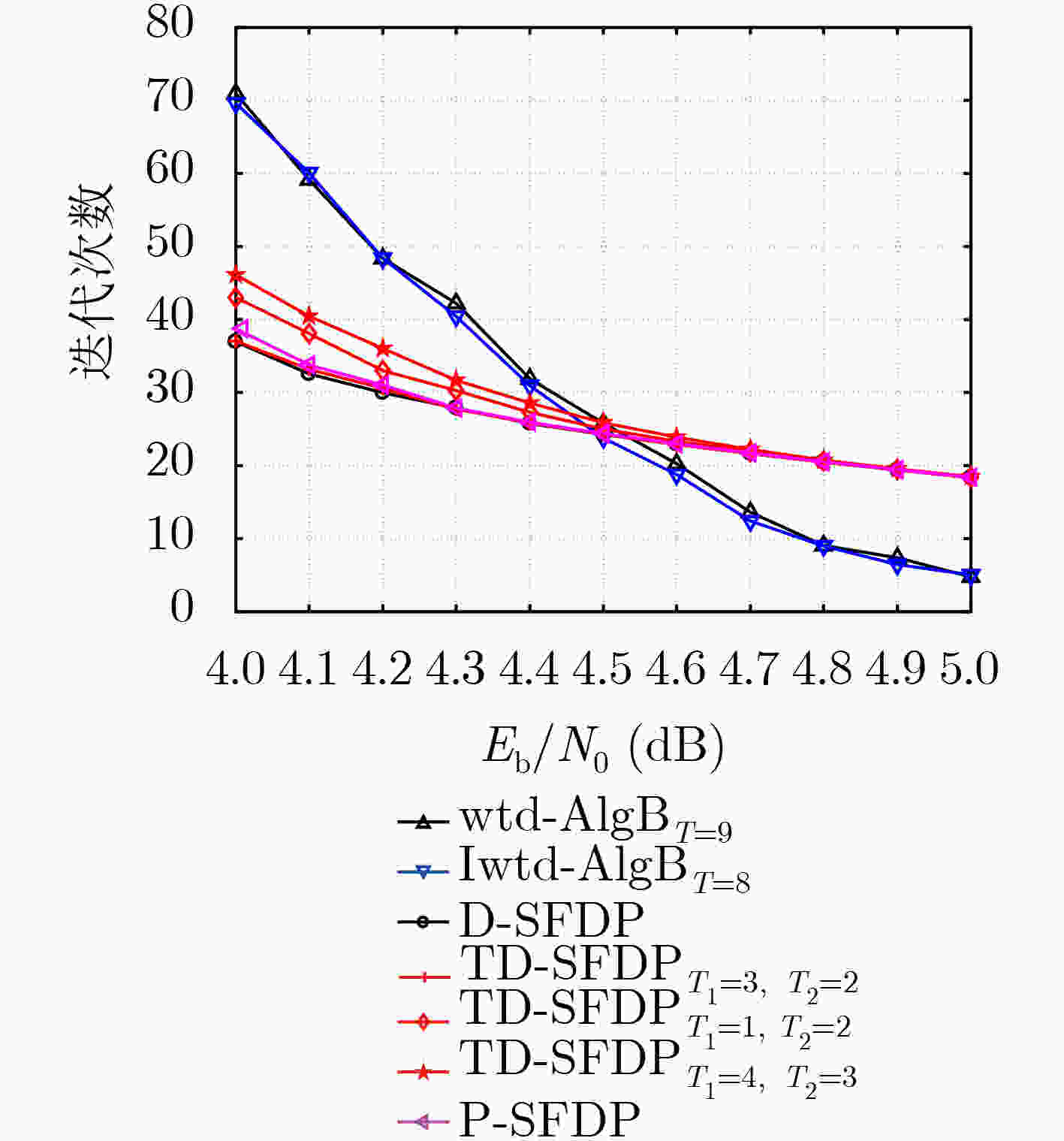
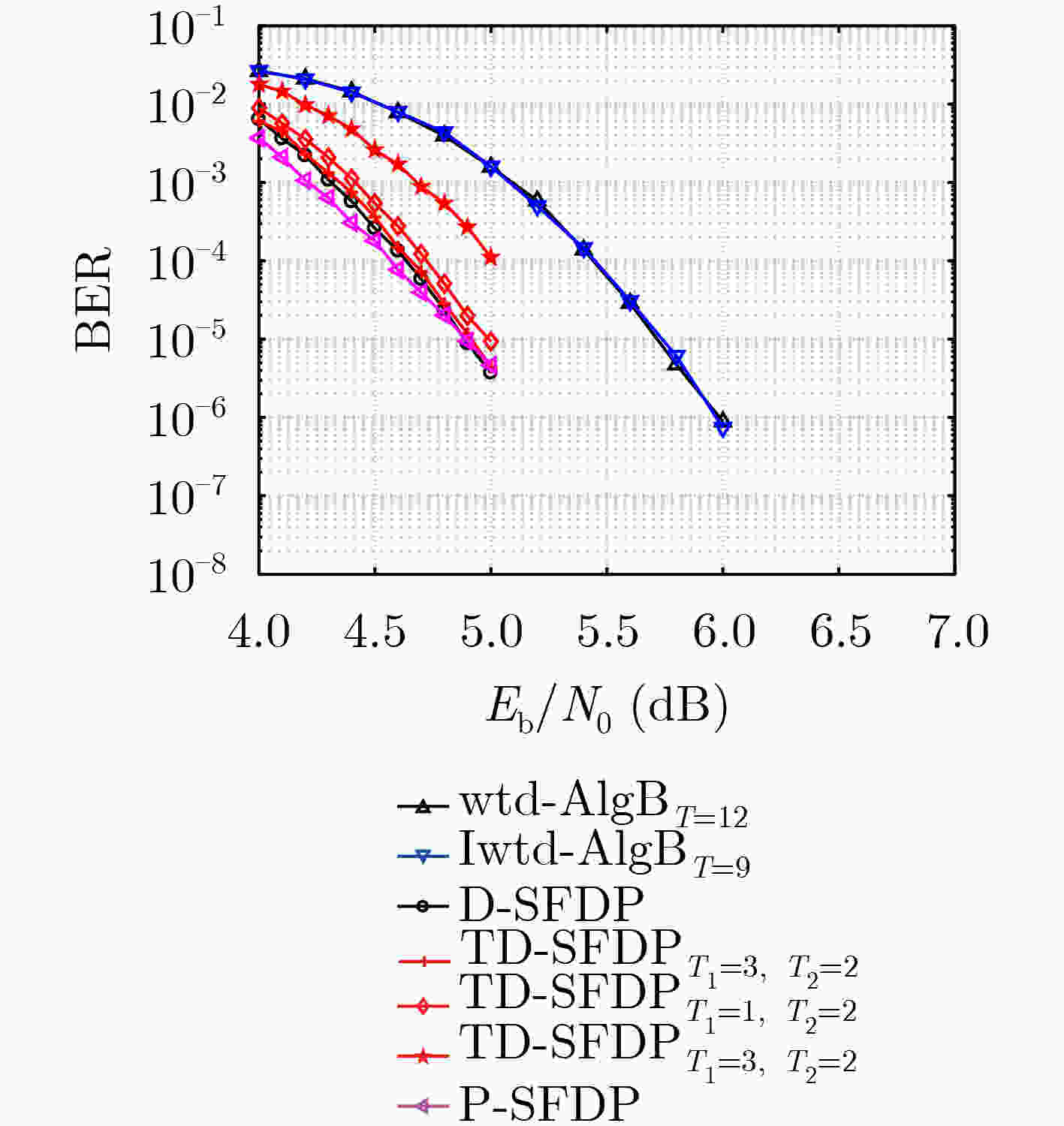
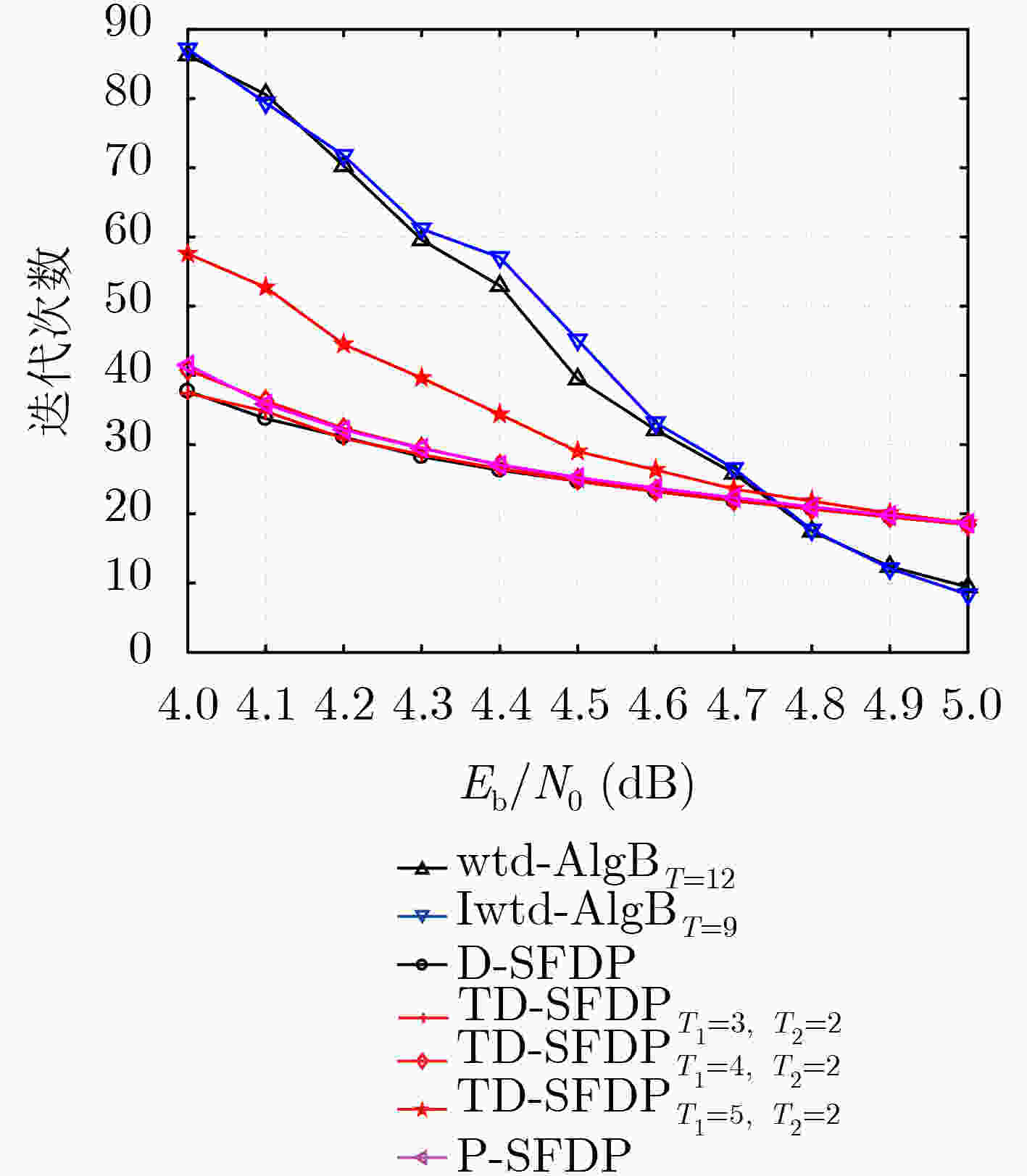
${F_{16}}(255,175)$ 多元LDPC码的每次迭代译码算法复杂度算法 每次迭代的运算操作数量 IM//RM GA GM IA//RA IC//RC wBRB $4080$ $7905$ $8160$ $32640$ $35955$ wtd-AlgB $4080$ $11985$ $8160$ $4080$ $4080$ Iwtd-AlgB $0$ $11985$ $8160$ $8160$ $4080$ P-SFDP $0$ $480$ $496$ $32053$ $5087$ D-SFDP $0$ $77600$ $496$ $104112$ $5087$ TD-SFDP $0$ $26880$ $496$ $42030$ $4288$ -
KOU Yu, LIN Shu, and FOSSORIER M P C. Low-density parity-check codes based on finite geometries: A rediscovery and new results[J]. IEEE Transactions on Information Theory, 2001, 47(7): 2711–2736. doi: 10.1109/18.959255 BARNAULT L and DECLERCQ D. Fast decoding algorithm for LDPC over GF (2q)[C]. 2013 IEEE Information Theory Workshop, Paris, France, 2013: 70–73. doi: 10.1109/ITW.2003.1216697. SONG Hongxin and CRUZ J R. Reduced-complexity decoding of Q-ary LDPC codes for magnetic recording[J]. IEEE Transactions on Magnetics, 2003, 39(2): 1081–1087. doi: 10.1109/TMAG.2003.808600 DECLERCQ D and FOSSORIER M. Decoding algorithms for non-binary LDPC codes over GF(q)[J]. IEEE Transactions on Communications, 2007, 55(4): 633–643. doi: 10.1109/TCOMM.2007.894088 MA Xiao, ZHANG Kai, CHEN Haiqiang, et al. Low complexity X-EMS algorithms for nonbinary LDPC codes[J]. IEEE Transactions on Communications, 2012, 60(1): 9–13. doi: 10.1109/TCOMM.2011.092011.110082 DEKA K, RAJESH A, and BORA P K. A novel truncation rule for the EMS decoding of non-binary LDPC codes[C]. 2018 International Conference on Signal Processing and Communications, Bangalore, India, 2018: 11–15. doi: 10.1109/SPCOM.2018.8724394. LI Yibing, ZHANG Sitong, YE Fang, et al. Improved extended min-sum algorithm for non-binary LDPC codes based on node reliability[C]. 2019 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications, Granada, Spain, 2019: 292–297. doi: 10.1109/APWC.2019.8870565. 杨威, 张为. 一种基于分层译码和Min-max的多进制LDPC码译码算法[J]. 电子与信息学报, 2013, 35(7): 1677–1681.YANG Wei and ZHANG Wei. A Decoding algorithm based on layered decoding and Min-max for nonbinary LDPC codes[J]. Journal of Electronics &Information Technology, 2013, 35(7): 1677–1681. SONG Liyuan, HUANG Qin, WANG Zulin, et al. Two enhanced reliability-based decoding algorithms for nonbinary LDPC codes[J]. IEEE Transactions on Communications, 2016, 64(2): 479–489. doi: 10.1109/TCOMM.2015.2512582 LI Xiangcheng, QIN Tuanfa, CHEN Haiqiang, et al. Hard-information bit-reliability based decoding algorithm for majority-logic decodable nonbinary LDPC codes[J]. IEEE Communications Letters, 2016, 20(5): 866–869. doi: 10.1109/LCOMM.2016.2537812 YEO S and PARK I C. Improved hard-reliability based majority-logic decoding for non-binary LDPC codes[J]. IEEE Communications Letters, 2017, 21(2): 230–233. doi: 10.1109/LCOMM.2016.2623783 RYBIN P and FROLOV A. On the decoding radius realized by low-complexity decoded non-binary irregular LDPC codes[C]. 2018 International Symposium on Information Theory and Its Applications, Singapore, 2018: 384–388. doi: 10.23919/ISITA.2018.8664375. JAGIELLO K and RYAN W E. Iterative plurality-logic and generalized algorithm B decoding of q-ary LDPC codes[C]. IEEE Information Theory and Applications Workshop, La Jolla, USA, 2011: 1–7. HUANG Chaocheng, WU C J, CHEN Chaoyu, et al. Parallel symbol-flipping decoding for non-binary LDPC codes[J]. IEEE Communications Letters, 2013, 17(6): 1228–1231. doi: 10.1109/LCOMM.2013.051313.130303 NHAN N Q, NGATCHED T M N, DOBRE O A, et al. Multiple-votes parallel symbol-flipping decoding algorithm for non-binary LDPC codes[J]. IEEE Communications Letters, 2015, 19(6): 905–908. doi: 10.1109/LCOMM.2015.2418260 GARCIA-HERRERO F, DECLERCQ D, and VALLS J. Non-binary LDPC decoder based on symbol flipping with multiple votes[J]. IEEE Communications Letters, 2014, 18(5): 749–752. doi: 10.1109/LCOMM.2014.030914.132867 WANG Shuai, HUANG Qin, and WANG Zulin. Symbol flipping decoding algorithms based on prediction for non-binary LDPC Codes[J]. IEEE Transactions on Communications, 2017, 65(5): 1913–1924. doi: 10.1109/TCOMM.2017.2677438 MU Haiwei, MENG Jiahui, ZHANG Liang, et al. Weighted symbol flipping decoding for non-binary LDPC codes based on iteration stopping criterion[C]. The 37th Chinese Control Conference, Wuhan, China, 2018: 8447–8452. doi: 10.23919/ChiCC.2018.8483599. DAI Bin, LIU Rongke, GAO Chenyu, et al. Symbol flipping algorithm with self-adjustment strategy for LDPC codes over GF(q)[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 7189–7193. doi: 10.1109/TVT.2019.2915802 OH J, HAN S, and HA J. An improved symbol-flipping algorithm for nonbinary LDPC codes and its application to NAND flash memory[J]. IEEE Transactions on Magnetics, 2019, 55(9): 3500113. doi: 10.1109/TMAG.2019.2918985 HUANG Qin, ZHANG Mu, WANG Zulin, et al. Bit-Reliability based low-complexity decoding algorithms for non-binary LDPC codes[J]. IEEE Transactions on Communications, 2014, 62(12): 4230–4240. doi: 10.1109/TCOMM.2014.2370032 ZENG Lingqi, LAN Lan, TAI Yingyu, et al. Transactions Papers - Constructions of nonbinary quasi-cyclic LDPC codes: A finite field approach[J]. IEEE Transactions on Communications, 2008, 56(4): 545–554. doi: 10.1109/TCOMM.2008.060024. ZENG Lingqi, LAN Lan, TAI Yingyu, et al. Construction of nonbinary cyclic, quasi-cyclic and regular LDPC codes: A finite geometry approach[J]. IEEE Transactions on Communications, 2008, 56(3): 378–387. doi: 10.1109/TCOMM.2008.060025 -






 下载:
下载:






 下载:
下载:
