A Kind of Versoria Function Normalized Adaptive Filtering Algorithm
-
摘要:
在综合考虑自适应滤波算法设计中收敛速度、稳态误差、计算复杂度和跟踪性能等指标的基础上,该文提出一种类箕舌线函数的变步长归一化自适应滤波算法,用类箕舌线函数代替Sigmoid函数作为步长迭代公式,引入基于相关误差的变步长调整原则,在大大增强算法稳定性的同时大幅度提升了算法的收敛速度、跟踪性能,减小了算法的计算复杂度。在Matlab平台上分析了改进的步长函数中参数
\begin{document}$\alpha $\end{document} ,
以及
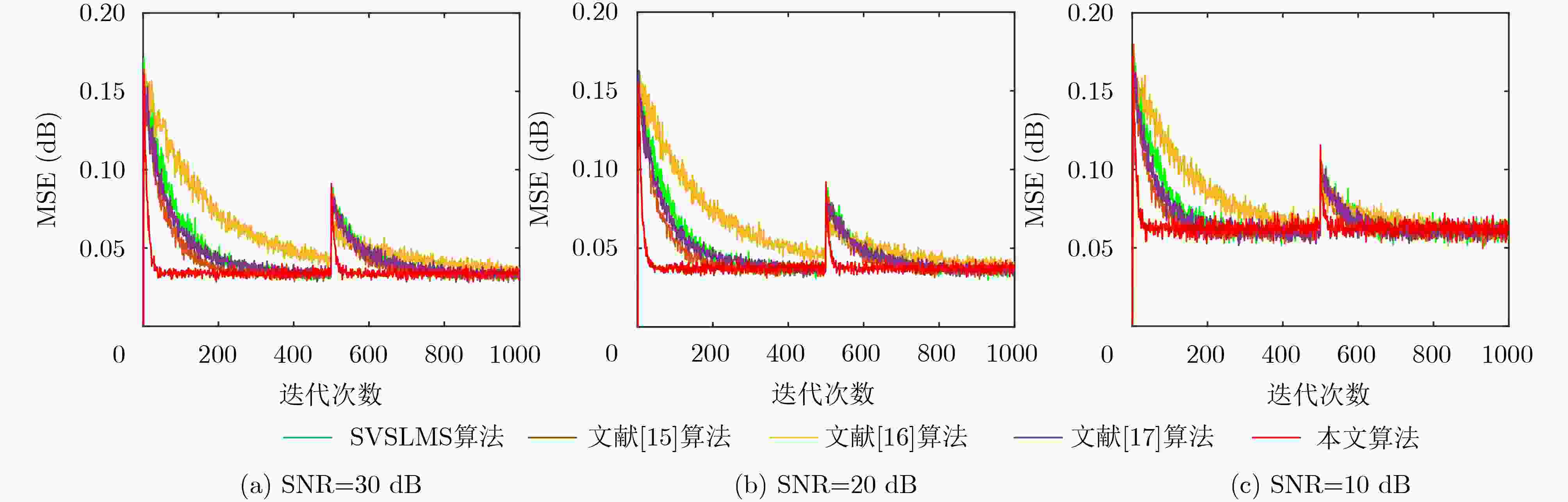
的不同取值对算法的影响,并将该文算法与已有的基于Sigmoid函数和基于箕舌线函数的变步长LMS算法进行了比较,仿真结果表明,该文算法有更快的收敛速度、更好的跟踪能力以及较小的稳态误差和较强的鲁棒性。
Abstract:On the basis of the comprehensive consideration in the design of the indexs of the adaptive filter algorithm convergence speed, steady-state error, computational complexity and tracking performance, a kind of Versoria function normalized adaptive filtering algorithm is proposed in this paper. The class Versoria function is used instead of Sigmoid function as step iterative formula, introducing variable step size based on the relevant error adjustment principle, the stability of the algorithm is enhanced greatly. At the same time, the convergence speed and tracking performance of the algorithm is promoted and the computational complexity of the algorithm is reduced. The influence of the parameter
\begin{document}$\alpha $\end{document} ,
and
different value of the step function of algorithm is analyzed on Matlab platform. Compared with the Sigmoid function variable step size LMS algorithm and variable step size LMS algorithm based on Versoria function, and the simulation results show that this algorithm has faster convergence speed, better tracking ability, smaller steady-state error and strong robustness.
-
孙慧贤, 刘建成, 崔佩璋, 等. 基于多通道最小均方算法的多发单收同车电台射频干扰对消[J]. 电子与信息学报, 2019, 41(3): 556–562. doi: 10.11999/JEIT180356SUN Huixian, LIU Jiancheng, CUI Peizhang, et al. RF interference cancellation based on multi-channel least mean square for multi-transmits and single-receive co-vehicle radios[J]. Journal of Electronics &Information Technology, 2019, 41(3): 556–562. doi: 10.11999/JEIT180356 赵杨, 尚朝轩, 韩壮志, 等. 分数阶傅里叶和压缩感知自适应抗频谱弥散干扰[J]. 电子与信息学报, 2019, 41(5): 1047–1054. doi: 10.11999/JEIT180569ZHAO Yang, SHANG Chaoxuan, HAN Zhuangzhi, et al. Fractional Fourier transform and compressed sensing adaptive countering smeared spectrum jamming[J]. Journal of Electronics &Information Technology, 2019, 41(5): 1047–1054. doi: 10.11999/JEIT180569 唐敏, 齐栋, 刘成城, 等. 基于多级阻塞的稳健相干自适应波束形成[J]. 电子与信息学报, 2019, 41(7): 1705–1711. doi: 10.11999/JEIT180332TANG Min, QI Dong, LIU Chengcheng, et al. New adaptive beamformer for coherent interference based on multistage blockin[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1705–1711. doi: 10.11999/JEIT180332 王世元, 史春芬, 蒋云翔, 等. 基于q梯度的仿射投影算法及其稳态均方收敛分析[J]. 电子与信息学报, 2018, 40(10): 2402–2407. doi: 10.11999/JEIT171125WANG Shiyuan, SHI Chunfen, JIANG Yunxiang, et al. q-affine projection algorithm and its steady-state mean square convergence analysis[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2402–2407. doi: 10.11999/JEIT171125 毕晓君, 王朝. 一种基于角度惩罚距离的高维多目标进化算法[J]. 电子与信息学报, 2018, 40(2): 314–322. doi: 10.11999/JEIT170454BI Xiaojun and WANG Chao. A many-objective evolutionary algorithm based on angle penalized distance[J]. Journal of Electronics &Information Technology, 2018, 40(2): 314–322. doi: 10.11999/JEIT170454 ZHENG Weixing. Adaptive filter design subject to output envelope constraints and bounded input noise[J]. IEEE Transactions on circuits and systems II: Analog and Digital Signal Processing, 2003, 50(12): 1023–1027. doi: 10.1109/tcsii.2003.820237 FENG Dazheng and ZHENG Weixing. Fast RLS-type algorithm for unbiased equation-error adaptive IIR filtering based on approximate inverse-power iteration[J]. IEEE Transactions on Signal Processing, 2005, 53(11): 4169–4185. doi: 10.1109/tsp.2005.857036 FENG D Z and ZHENG W X. Fast approximate inverse power iteration algorithm for adaptive total least-squares FIR filtering[J]. IEEE Transactions on Signal Processing, 2006, 54(10): 4032–4039. doi: 10.1109/tsp.2006.880245 SONG Xinmin and PARK J H. Linear minimum mean-square estimation for discrete-time measurement-delay systems with multiplicative noise and Markov jump[J]. IET Control Theory & Applications, 2016, 10(10): 1161–1169. doi: 10.1049/iet-cta.2015.1197 于霞, 刘建昌, 李鸿儒. 基于箕舌线函数的快速凸组合最小均方算法[J]. 系统仿真学报, 2010, 22(5): 1097–1100, 1105.YU Xia, LIU Jianchang, and LI Hongru. Fast convex combination of least-mean-square algorithm based on versoria function[J]. Journal of System Simulation, 2010, 22(5): 1097–1100, 1105. ABBAS H and HAI Huang. Weight size determined variable step size LMS method for identifying under damped systems[J]. Applied Mechanics and Materials, 2014, 511–512: 238–241. doi: 10.4028/www.scientific.net/AMM.511-512.238 高鹰, 谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报, 2001, 29(8): 1094–1097. doi: 10.3321/j.issn:0372-2112.2001.08.023GAO Ying and XIE Shengli. A variable step size LMS adaptive filtering algorithm and its analysis[J]. Acta Electronica Sinica, 2001, 29(8): 1094–1097. doi: 10.3321/j.issn:0372-2112.2001.08.023 仝喜峰, 陈卫松, 钱隆彦, 等. 一种非线性变步长LMS自适应滤波算法[J]. 无线电通信技术, 2019, 45(4): 391–396. doi: 10.3969/j.issn.1003-3114.2019.04.011TONG Xifeng, CHEN Weisong, QIAN Longyan, et al. A nonlinear variable step size LMS adaptive filtering algorithm[J]. Radio Communications Technology, 2019, 45(4): 391–396. doi: 10.3969/j.issn.1003-3114.2019.04.011 覃景繁, 欧阳景正. 一种新的变步长LMS自适应滤波算法[J]. 数据采集与处理, 1997, 12(3): 171–174.QIN Jingfan and OUYANG Jingzheng. A novel variable step size LMS adaptive filtering algorithm based on sigmoid function[J]. Journal of Data Acquisition &Processing, 1997, 12(3): 171–174. 刘宪爽, 吴华明, 肖文波, 等. 改进的双Sigmoid函数变步长自适应算法及在OCT中的应用[J]. 电子学报, 2019, 47(1): 234–240. doi: 10.3969/j.issn.0372-2112.2019.01.031LIU Xianshuang, WU Huaming, XIAO Wenbo, et al. Improved double sigmoid function variable step size adaptive algorithm and its application in OCT[J]. Acta Electronica Sinica, 2019, 47(1): 234–240. doi: 10.3969/j.issn.0372-2112.2019.01.031 邓江波, 侯新国, 吴正国. 基于箕舌线的变步长LMS自适应算法[J]. 数据采集与处理, 2004, 19(3): 282–285. doi: 10.3969/j.issn.1004-9037.2004.03.010DENG Jiangbo, HOU Xinguo, and WU Zhengguo. Variable step adaptive filtering LMS algorithm based on tongue-like curve[J]. Journal of Data Acquisition &Processing, 2004, 19(3): 282–285. doi: 10.3969/j.issn.1004-9037.2004.03.010 韩允, 解传军, 刘宝华, 等. 基于箕舌线函数的变步长归一化最小均方算法[J]. 现代电子技术, 2008, 31(19): 29–32. doi: 10.3969/j.issn.1004-373X.2008.19.010HAN Yun, XIE Chuanjun, LIU Baohua, et al. Modified variable step-size normalized least-mean-square algorithm based on versoria function[J]. Modern Electronics Technique, 2008, 31(19): 29–32. doi: 10.3969/j.issn.1004-373X.2008.19.010 陈泳, 田金鹏, 刘燕平. 一种新的变步长LMS自适应滤波算法[J]. 电子测量技术, 2015, 38(4): 27–31. doi: 10.3969/j.issn.1002-7300.2015.04.007CHEN Yong, TIAN Jinpeng, and LIU Yanping. New variable step size LMS adaptive filtering algorithm[J]. Electronic Measurement Technology, 2015, 38(4): 27–31. doi: 10.3969/j.issn.1002-7300.2015.04.007 YASUKAWA H, SHIMADA S, and FURUKAWA I. Acoustic echo canceller with high speech quality[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, USA, 1987: 2125–2128. doi: 10.1109/ICASSP.1987.1169314. 叶华, 吴伯修. 变步长自适应滤波算法的研究[J]. 电子学报, 1990, 18(4): 63–70. doi: 10.3321/j.issn:0372-2112.1990.04.012YE Hua and WU Boxiu. The study on a variable step size adaptive filtering algorithm[J]. Acta Electronica Sinica, 1990, 18(4): 63–70. doi: 10.3321/j.issn:0372-2112.1990.04.012 GITLIN R, MAZO J, and TAYLOR M. On the design of gradient algorithms for digitally implemented adaptive filters[J]. IEEE Transactions on Circuit Theory, 1973, 20(2): 125–136. doi: 10.1109/tct.1973.1083627 耿艳香, 徐文超, 张铮, 等. 基于箕舌线函数的变步长自适应均衡的研究[J]. 实验室科学, 2010, 13(4): 111–113. doi: 10.3969/j.issn.1672-4305.2010.04.037GENG Yanxiang, XU Wenchao, ZHANG Zheng, et al. Research on the variable step adaptive equalizer based on Versoria function[J]. Laboratory Science, 2010, 13(4): 111–113. doi: 10.3969/j.issn.1672-4305.2010.04.037 -





 下载:
下载:






 下载:
下载:
