Design of a Multi-scroll Chaotic System and its Application to Image Encryption
-
摘要:
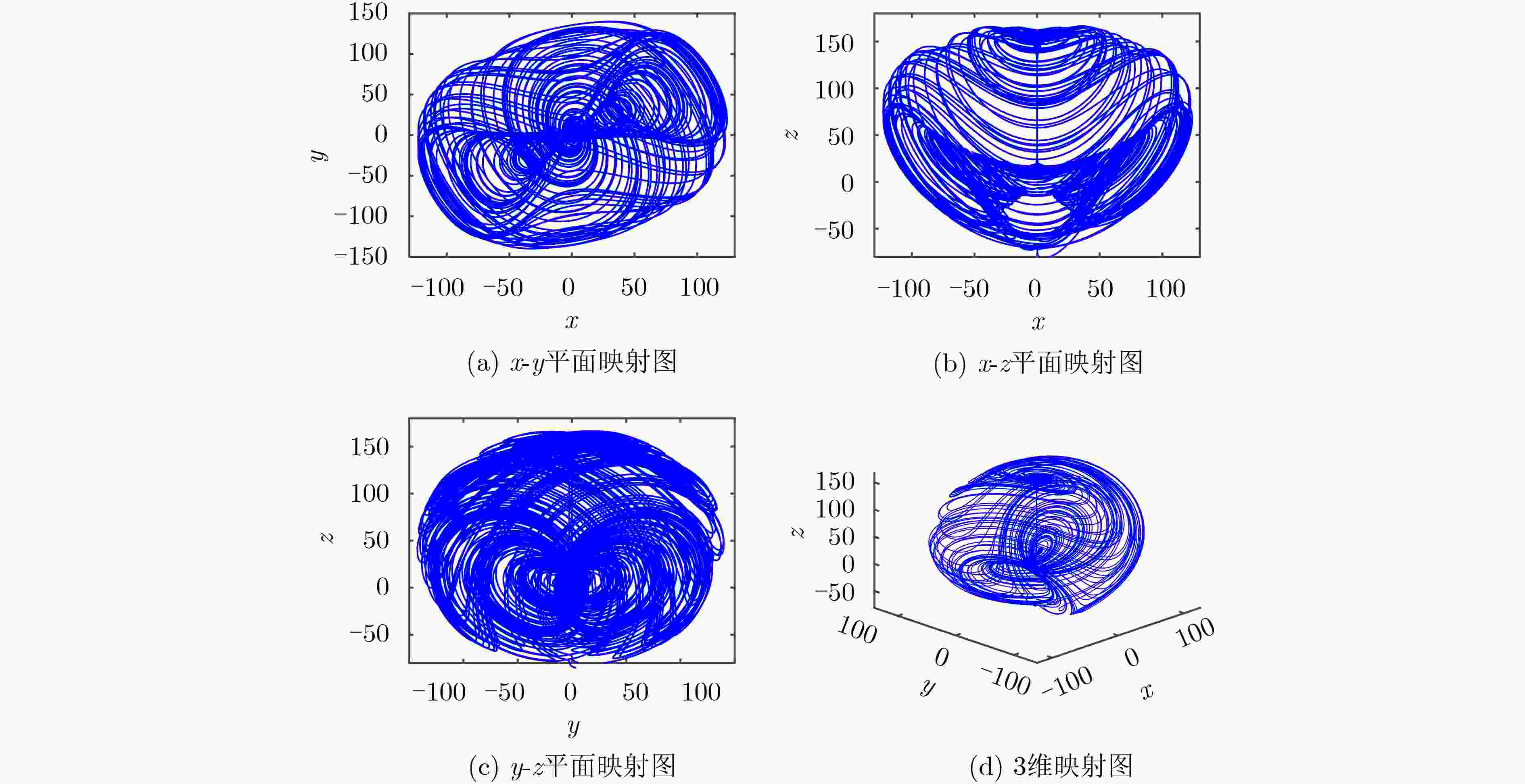
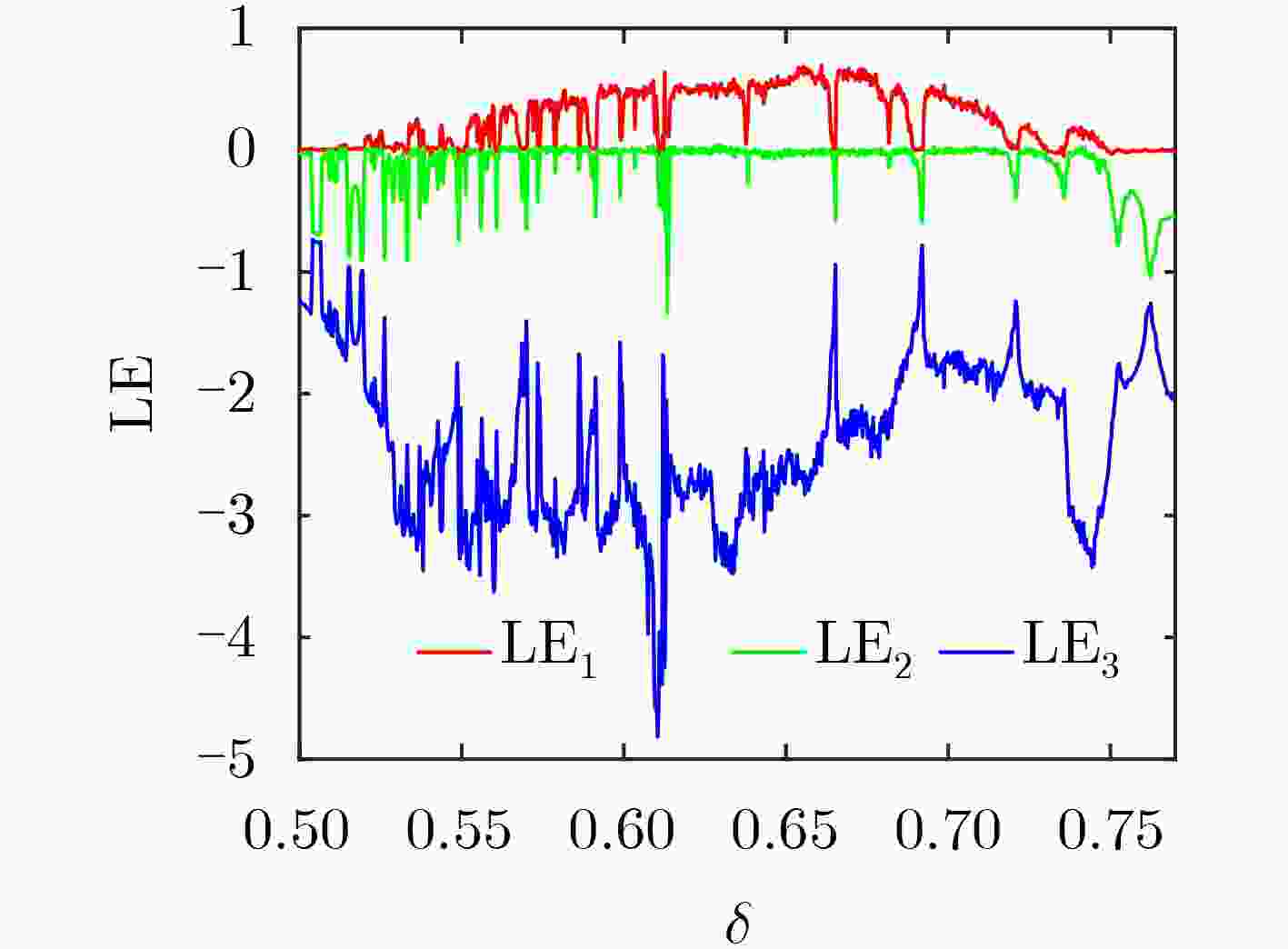
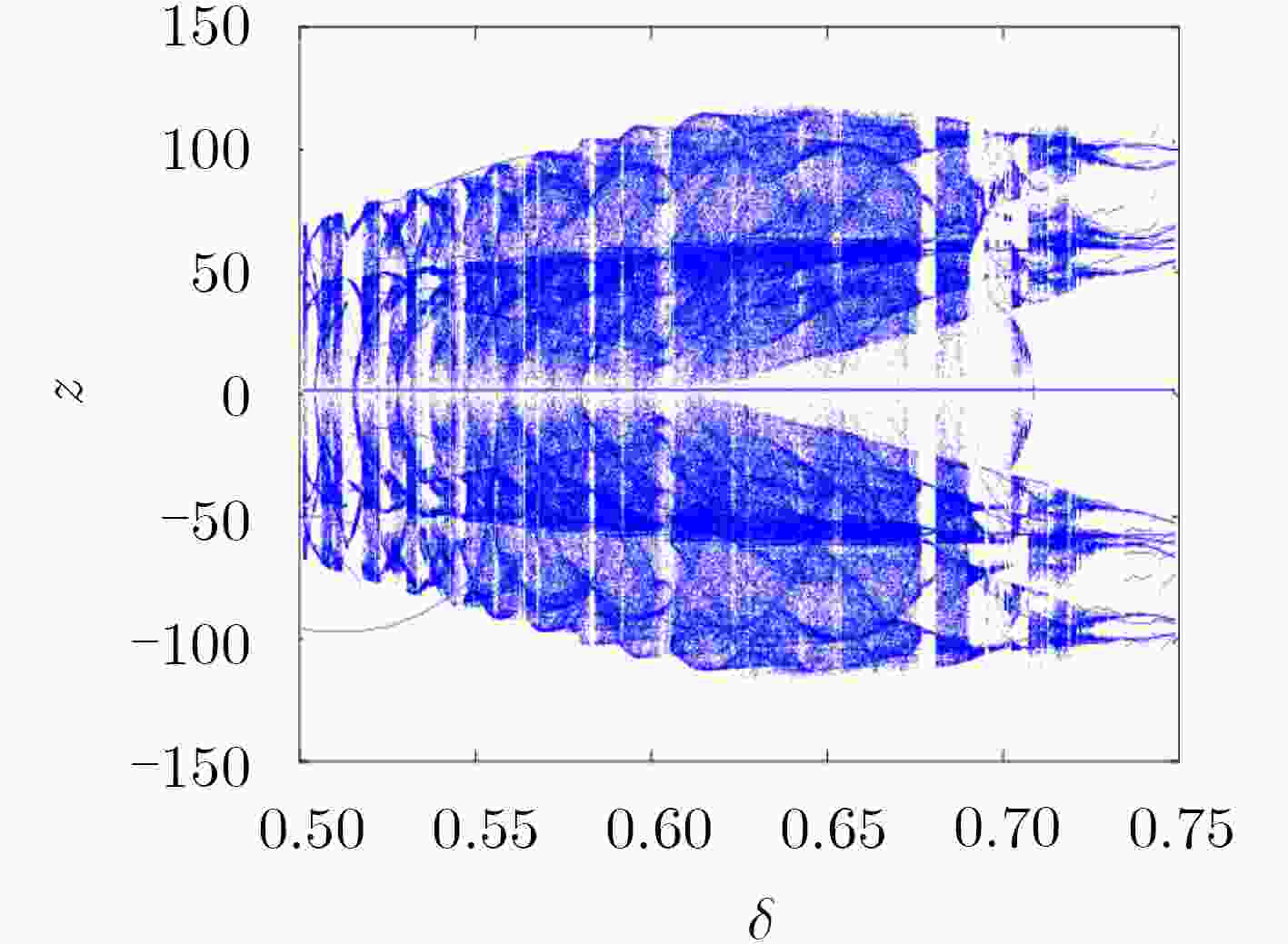
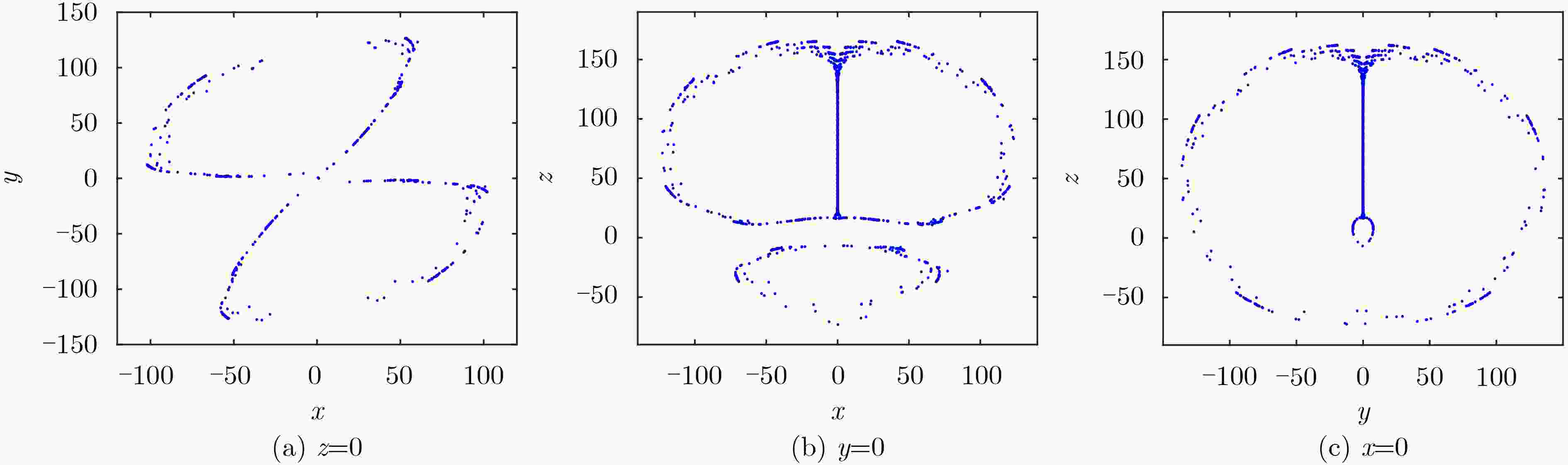
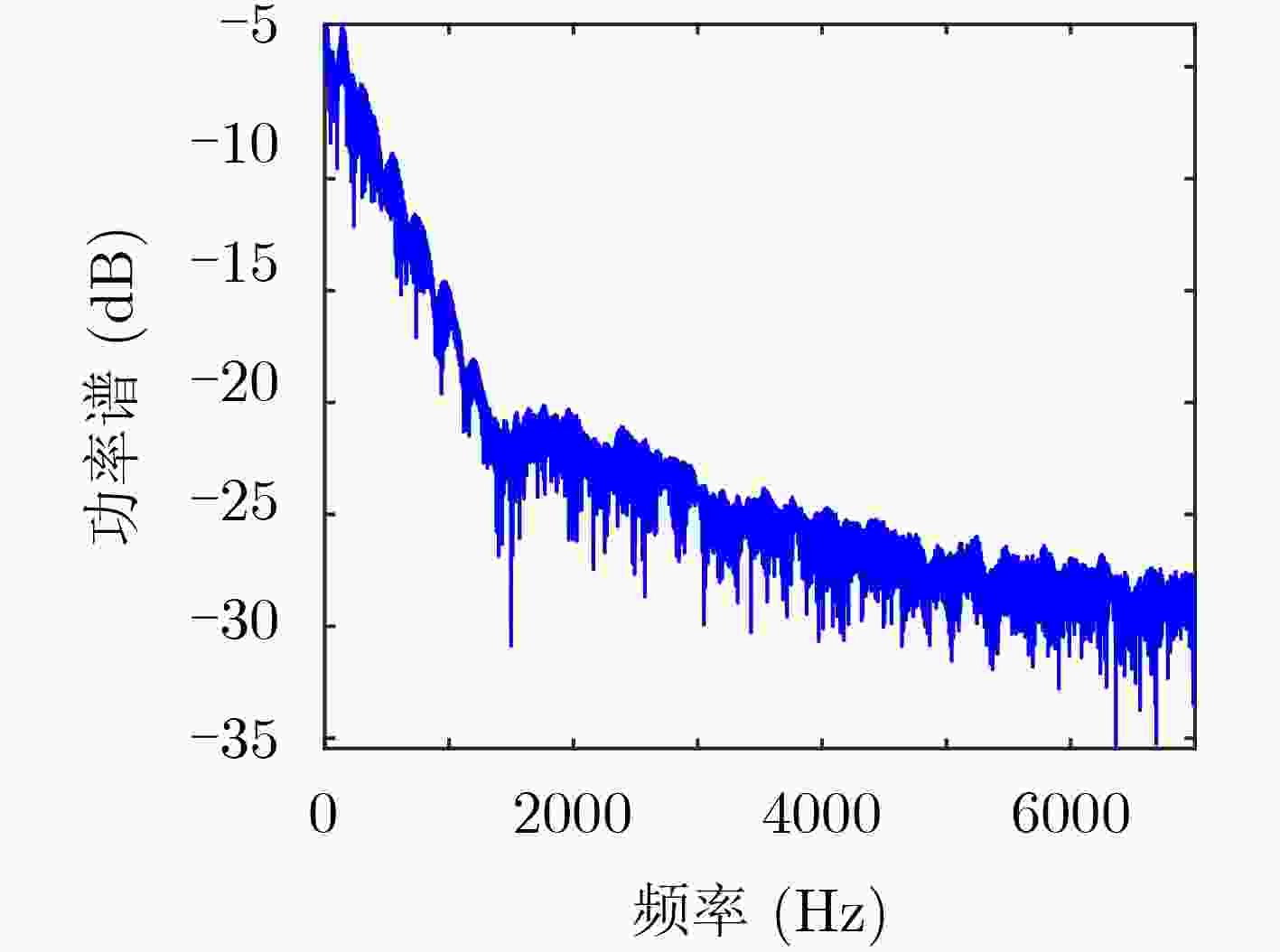
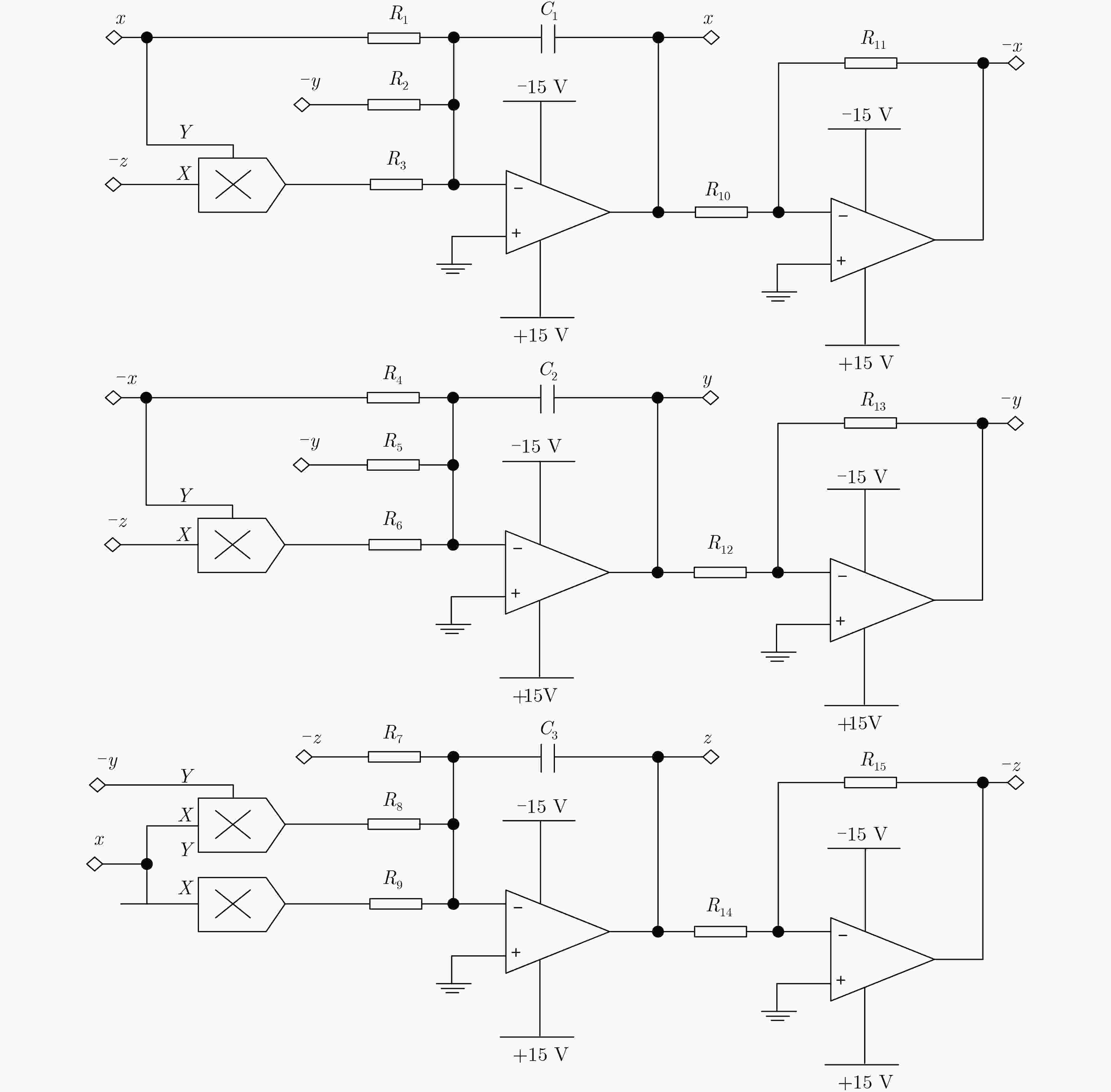
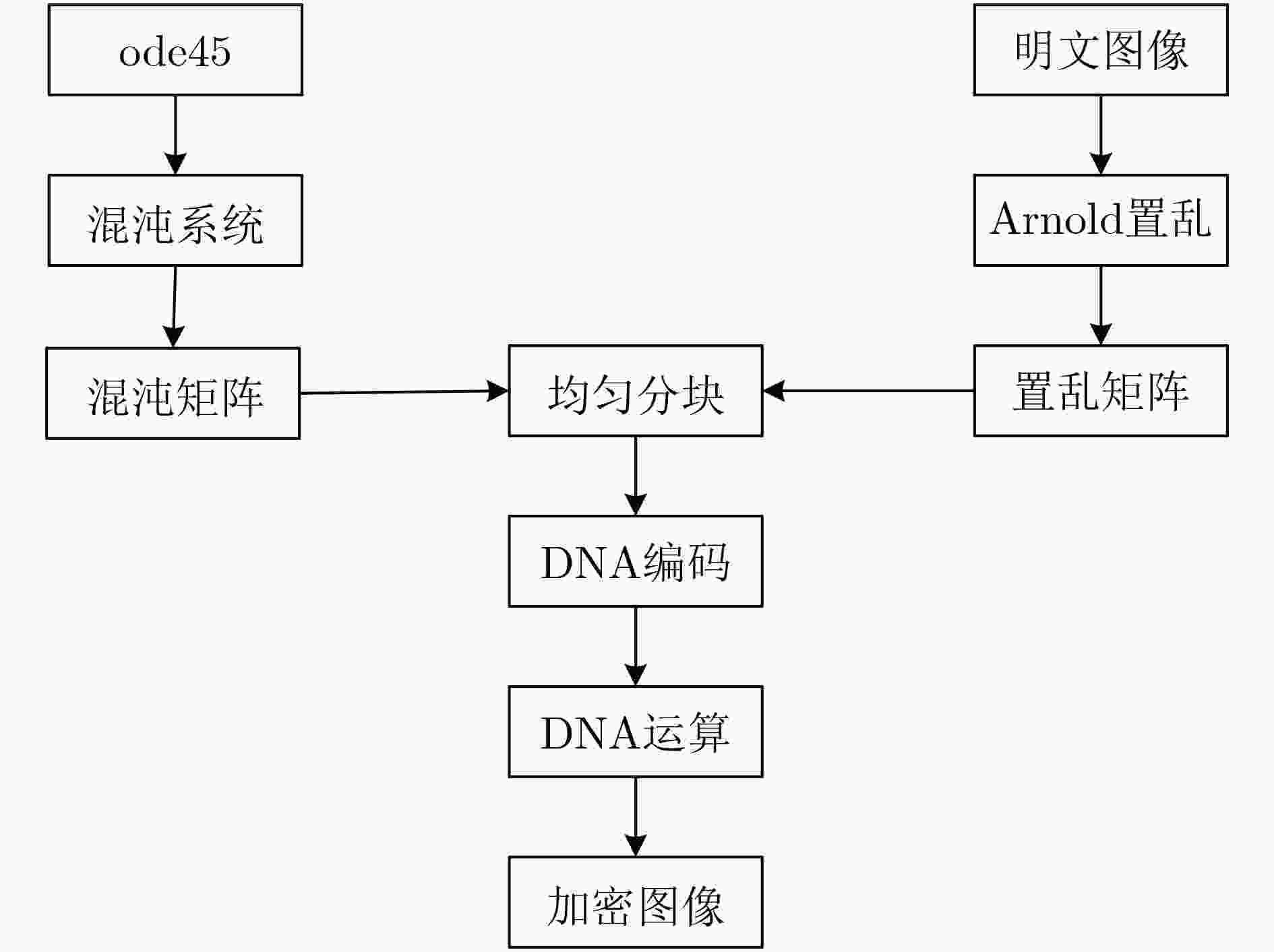
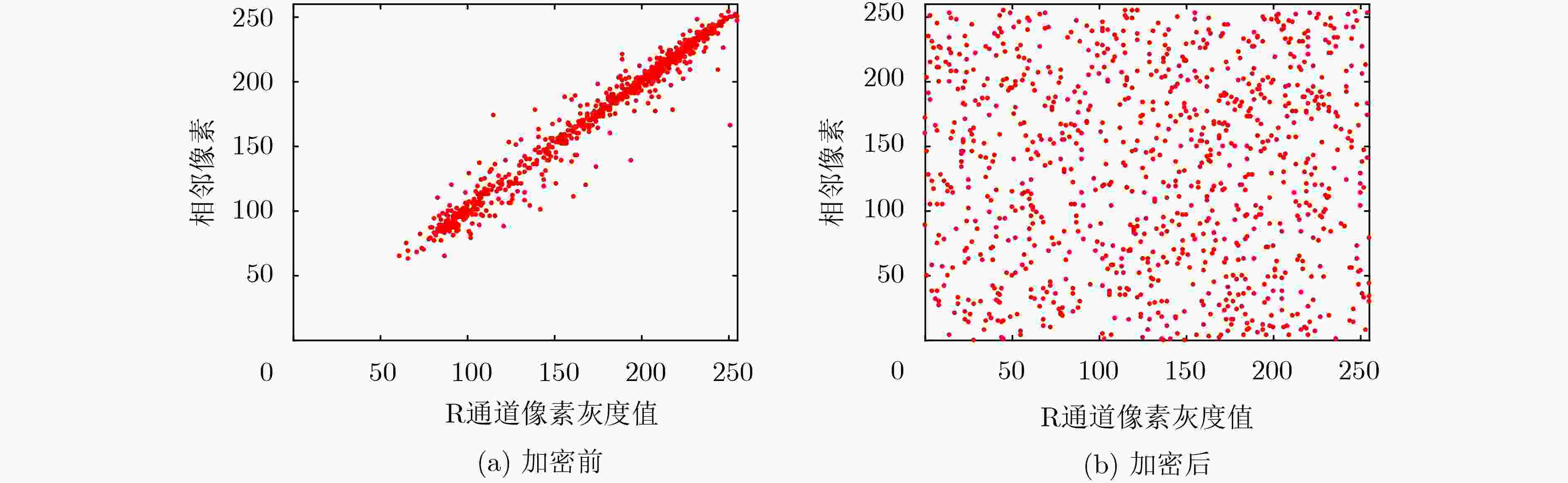
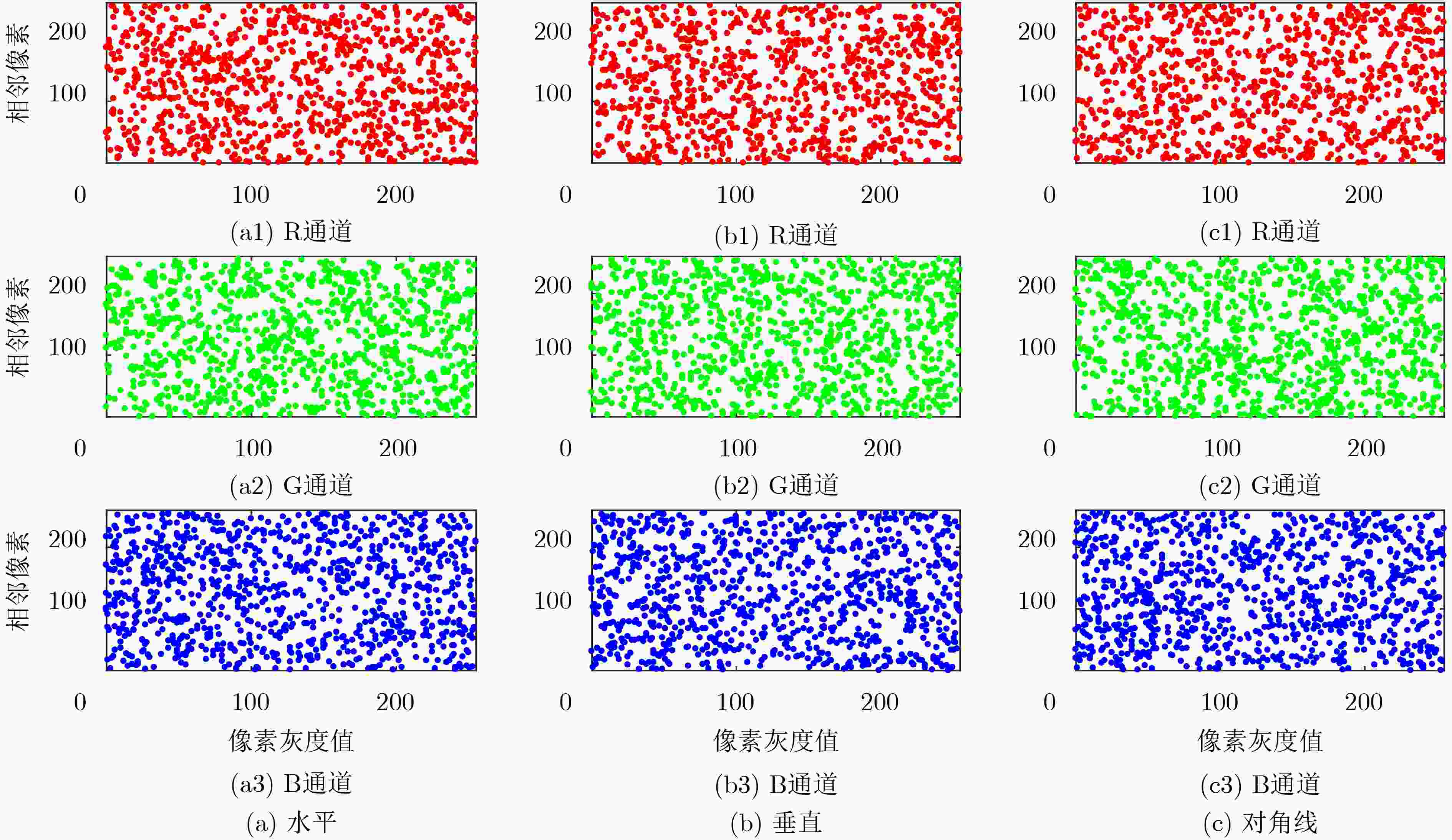
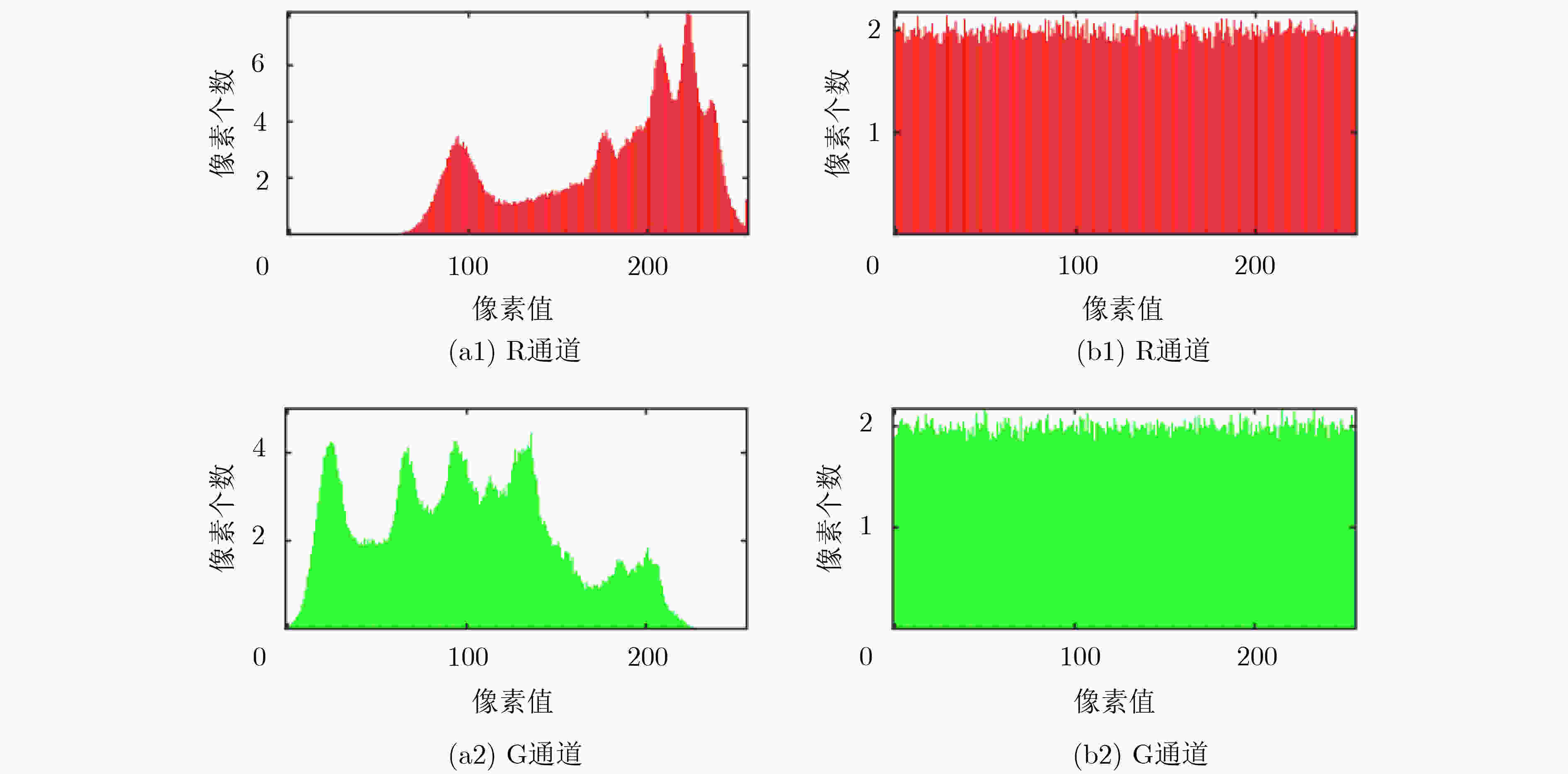
该文提出一种三涡卷混沌系统,首先对系统的李雅普诺夫指数、分岔图、Poincare截面图、功率谱图及平衡点稳定性等动力学特性进行了理论分析和数值仿真,结果表明该系统具有良好的动力学特性和丰富的拓扑吸引子。基于电路仿真软件Multisim研制了实验仿真电路, 该电路结构简单、易于实际制作,且仿真实验与理论分析结论十分吻合,证实了提出的混沌系统电路在物理上是可以实现的,从而验证了该混沌系统的混沌产生能力。最后结合DNA算法设计了一种彩色图像加密算法,利用新系统混沌序列对图像进行加密,重点分析了加密直方图、相邻像素相关性。结果表明,新系统对混沌密钥及明文都非常敏感,密钥空间较大,提出的混沌系统应用于图像加密具有较高的安全性能。
Abstract:A chaotic system with three scrolls is proposed. The dynamics characteristics of the system, such as Lyapunov index, bifurcation diagram, Poincare cross section diagram, power spectrum and equilibrium stability, are studied by numerical simulation. The analysis results show that the system has good dynamics characteristics and rich topological attractors. In addition, an experimental simulation circuit is developed based on the circuit simulation software Multisim, which has a simple structure and is easy to realize in practice. Moreover, the simulation experiment is very consistent with the theoretical analysis conclusion, confirming that the proposed chaotic system circuit can be realized physically, thus verifying the chaos generation capacity of the chaotic system. Finally, a color image encryption algorithm is designed based on DNA algorithm, and the results show that the system has high security performance.Using the new system chaotic sequence to encrypt image, the encryption histogram and correlation between adjacent pixels are analyzed, results show that the new systems are very sensitive to image key and plaintext, key space is large, chaotic system applied to image encryption has higher safety performance.
-
Key words:
- Image encryption /
- Multi-scrolls /
- Chaotic system /
- Dynamical behavior /
- Circuit implementation
-
表 1 相邻像素在不同方向上的相关系数
-
MOOTHATHU T K S. Stronger forms of sensitivity for dynamical systems[J]. Nonlinearity, 2007, 20(9): 2115–2126. doi: 10.1088/0951-7715/20/9/006 李志军, 曾以成. 基于文氏振荡器的忆阻混沌电路[J]. 电子与信息学报, 2014, 36(1): 88–93. doi: 10.3724/SP.J.1146.2013.00332LI Zhijun and ZENG Yicheng. A memristor chaotic circuit based on Wien-bridge oscillator[J]. Journal of Electronics &Information Technology, 2014, 36(1): 88–93. doi: 10.3724/SP.J.1146.2013.00332 LÜ Jinhu and CHEN Guanrong. A new chaotic attractor coined[J]. International Journal of Bifurcation and Chaos, 2002, 12(3): 659–661. doi: 10.1142/S0218127402004620 BANERJEE T, BISWAS D, and SARKAR B C. Design and analysis of a first order time-delayed chaotic system[J]. Nonlinear Dynamics, 2012, 70(1): 721–734. doi: 10.1007/s11071-012-0490-3 VAIDYANATHAN S. A new six-term 3-d chaotic system with an exponential nonlinearity[J]. Far East Journal of Mathematical Sciences, 2013, 79(1): 135–145. 张平伟, 唐国宁, 罗晓曙. 双向耦合混沌系统广义同步[J]. 物理学报, 2005, 54(8): 3497–3501. doi: 10.3321/j.issn:1000-3290.2005.08.005ZHANG Pingwei, TANG Guoning, and LUO Xiaoshu. Generalized synchronization of bidirectionally coupled chaos systems[J]. Acta Physica Sinica, 2005, 54(8): 3497–3501. doi: 10.3321/j.issn:1000-3290.2005.08.005 李付鹏, 刘敬彪, 王光义, 等. 基于混沌集的图像加密算法[J]. 电子与信息学报, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344LI Fupeng, LIU Jingbiao, WANG Guangyi, et al. An image encryption algorithm based on chaos set[J]. Journal of Electronics &Information Technology, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344 LI Chengqing, LIN Dongdong, and LÜ Jinhu. Cryptanalyzing an image-scrambling encryption algorithm of pixel bits[J]. IEEE MultiMedia, 2017, 24(3): 64–71. doi: 10.1109/MMUL.2017.3051512 VOLOS C K, KYPRIANIDIS I M, and STOUBOULOS I N. Text encryption scheme realized with a chaotic pseudo-random bit generator[J]. Journal of Engineering Science and Technology Review, 2013, 6(4): 9–14. doi: 10.25103/jestr.064.02 YI Shuang and ZHOU Yicong. Binary-block embedding for reversible data hiding in encrypted images[J]. Signal Processing, 2017, 133: 40–51. doi: 10.1016/j.sigpro.2016.10.017 WANG Xingyuan, LIU Lintao, and ZHANG Yingqian. A novel chaotic block image encryption algorithm based on dynamic random growth technique[J]. Optics and Lasers in Engineering, 2015, 66: 10–18. doi: 10.1016/j.optlaseng.2014.08.005 段欢, 郑紫微. 基于位平面Arnold置乱变换改进算法[J]. 无线通信技术, 2018, 27(2): 37–42. doi: 10.3969/j.issn.1003-8329.2018.02.008DUAN Huan and ZHENG Ziwei. Improved algorithm of Arnold scrambling transformation based on bit plane[J]. Wireless Communication Technology, 2018, 27(2): 37–42. doi: 10.3969/j.issn.1003-8329.2018.02.008 KAMELl MOHAMED F. A parallel block-based encryption schema for digital images using reversible cellular automata[J]. Engineering Science & Technology An International Journal, 2014, 17(2): 85–94. doi: 10.1016/j.jestch.2014.04.001 李琳, 孔留勇. 一种基于混沌的新型图像加密算法[J]. 系统仿真学报, 2008, 30(3): 954–961. doi: 10.16182/j.issn1004731x.joss.201803023LI Lin and KONG Liuyong. A new image encryption algorithm based on chaos[J]. Journal of System Simulation, 2008, 30(3): 954–961. doi: 10.16182/j.issn1004731x.joss.201803023 闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178MIN Fuhong, WANG Zhulin, WANG Enrong, et al. New memristor chaotic circuit and its application to image encryption[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178 屈双惠, 杨志宏, 容旭巍, 等. 一个新忆阻混沌系统及其在图像加密中的应用[J]. 系统仿真学报, 2019, 31(5): 984–991. doi: 10.16182/j.issn1004731x.joss.17-0170QU Shuanghui, YANG Zhihong, RONG Xuwei, et al. A new memristor chaotic system and its application in image encryption[J]. Journal of System Simulation, 2019, 31(5): 984–991. doi: 10.16182/j.issn1004731x.joss.17-0170 朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法[J]. 电子与信息学报, 2012, 34(7): 1735–1743. doi: 10.3724/SP.J.1146.2011.01004ZHU Congxu, HU Yuping, and SUN Kehui. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern[J]. Journal of Electronics &Information Technology, 2012, 34(7): 1735–1743. doi: 10.3724/SP.J.1146.2011.01004 ENAYATIFAR R, ABDULL A H, and ISNIN I F. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence[J]. Optics and Lasers in Engineering, 2014, 56: 83–93. doi: 10.1016/j.optlaseng.2013.12.003 PING Ping, XU Feng, and WANG Zhijian. Image encryption based on non-affine and balanced cellular automata[J]. Signal Processing, 2014, 105: 419–429. doi: 10.1016/j.sigpro.2014.06.020 ZHANG Qiang, LIU Lili, and WEI Xiaopeng. Improved algorithm for image encryption based on DNA encoding and multi-chaotic maps[J]. AEU–International Journal of Electronics and Communications, 2014, 68(3): 186–192. doi: 10.1016/j.aeue.2013.08.007 -





 下载:
下载:







 下载:
下载:
