Physical Layer Secure Transmission Scheme with Joint Polar Codes and Non-reconciliation Secret Keys
-
摘要:
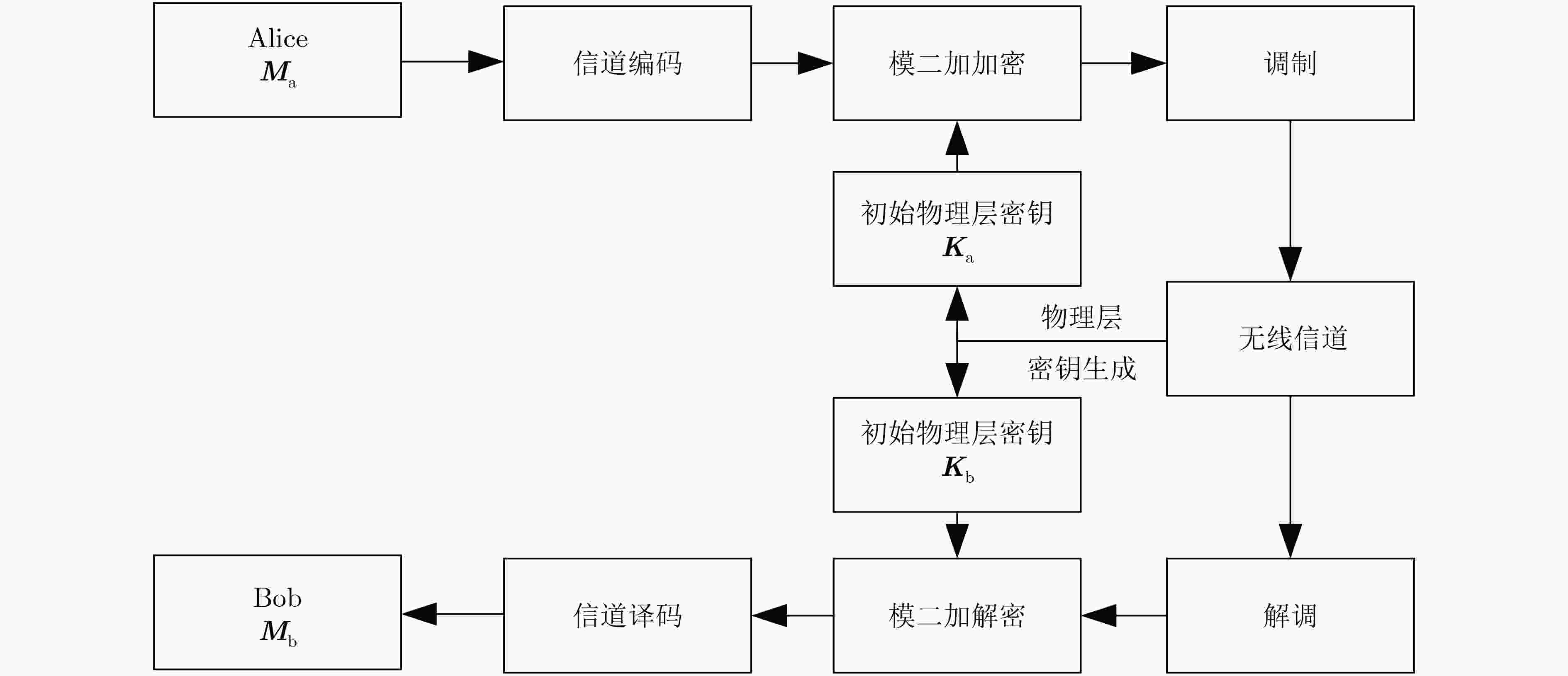
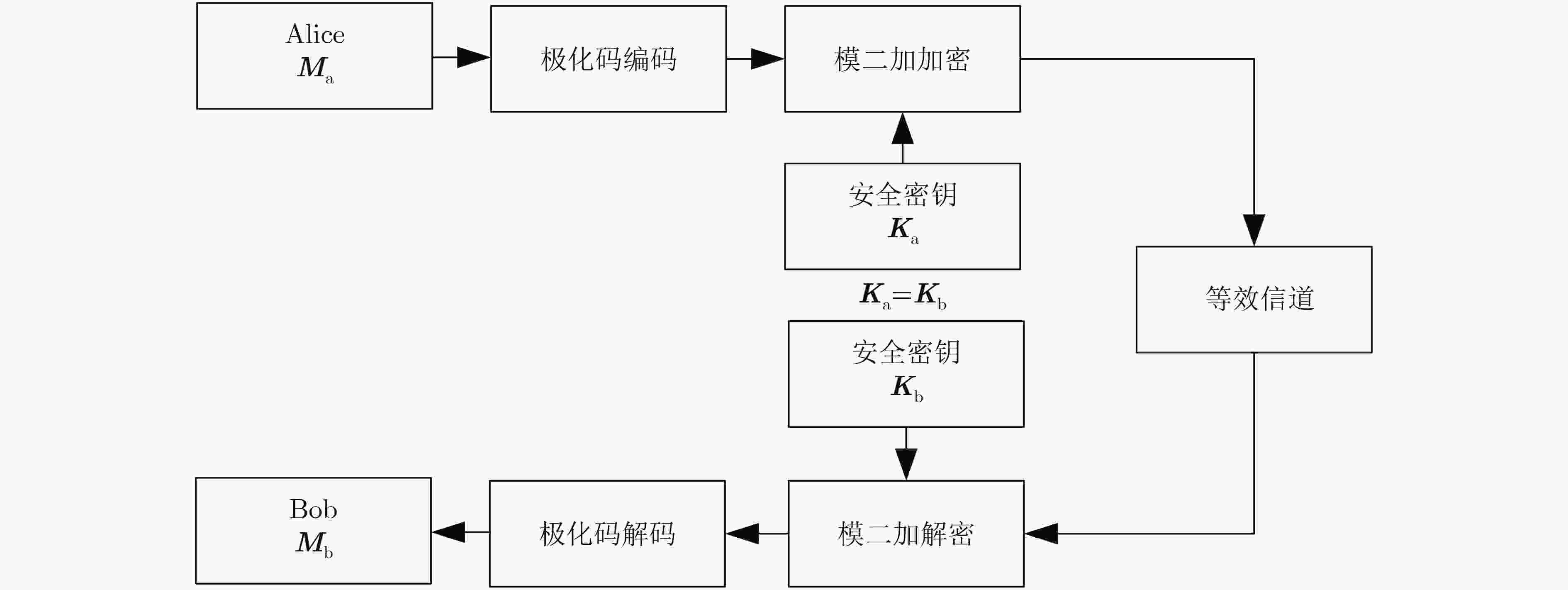
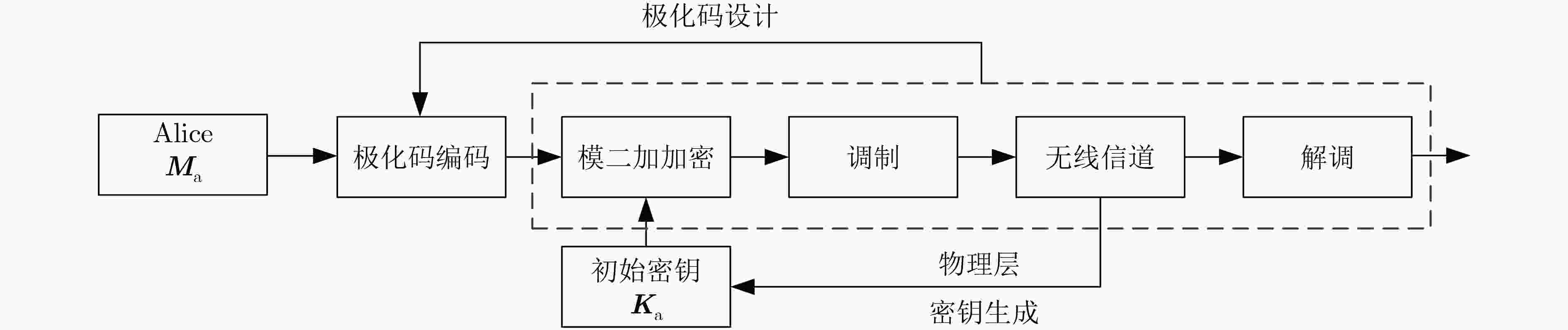
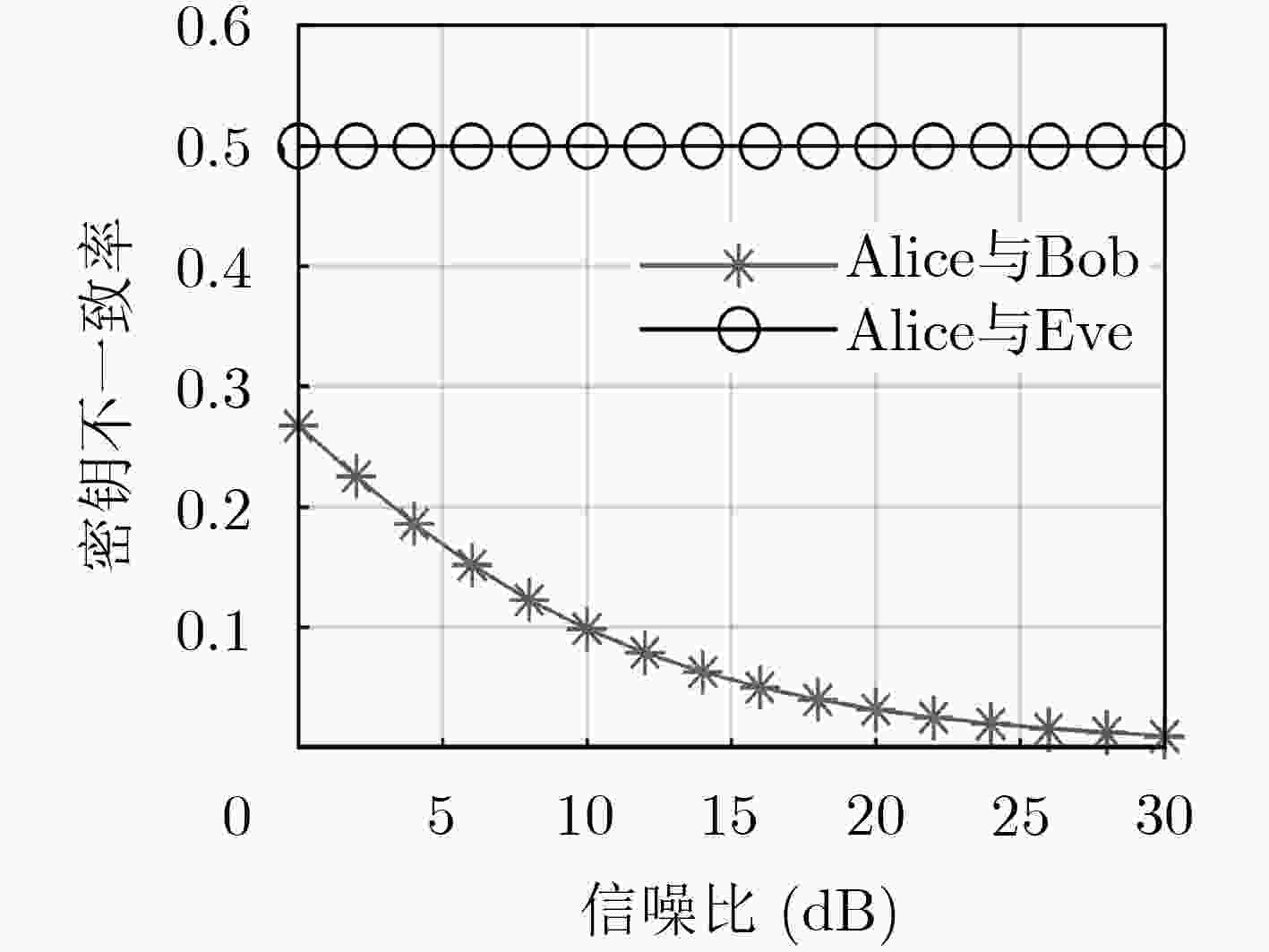
针对现有的密钥生成方案需要在通信流程中增加额外的密钥协商协议,导致在5G等标准通信系统中应用受限的问题,该文提出一种基于极化码的无协商密钥物理层安全传输方案。首先基于信道特征提取未协商的物理层密钥,然后针对物理信道与密钥加密信道共同构成的等效信道设计极化码,最后利用未协商的物理层密钥对编码后的序列进行简单的模二加加密后传输。该方案通过针对性设计的极化码纠正密钥差异和噪声引起的比特错误,实现可靠的安全传输。仿真表明,该文基于等效信道设计的极化码在保证合法双方以最优的码率可靠传输的同时可以防止窃听者窃听,实现了安全与通信的一体化。
Abstract:The existing key generation scheme requires additional key reconciliation protocol in a communication process, resulting in the limited application to the communication system, such as the Fifth-Generation mobile communication (5G). A physical layer secure transmission scheme with a joint polar code and non-reconciliation secret keys is proposed. Firstly, the non-reconciliation physical layer keys are extracted from the channel feature, and then the polar code is designed based on the equivalent channel, which is formed by the physical channel and the key encryption channel. Finally, the encoded sequence is simply modular plus encrypted and transmitted using the non-reconciliation physical layer key. Key differences and noise-induced bit errors are corrected through a targeted design of polarization codes to achieve reliable and secure transmission. The simulation shows that the polar code based on the equivalent channel can ensure the reliable transmission between two legitimate users at the optimal code rate.
-
表 1 仿真参数列表
仿真参数 设定值 天线数 单天线 无线信道 瑞利平衰落信道 极化码长 $N = 512$ 蒙特卡洛实验次数 ${10^8}$ 量化级数 1 bit量化 噪声功率 $\sigma _{\rm{w}}^2 = 1$ 功率分配 ${\sigma^2_{\rm{A} } }{\rm{ = } }{\sigma^2_{\rm{B} } }$ 表 2 极化码参数与设计性能
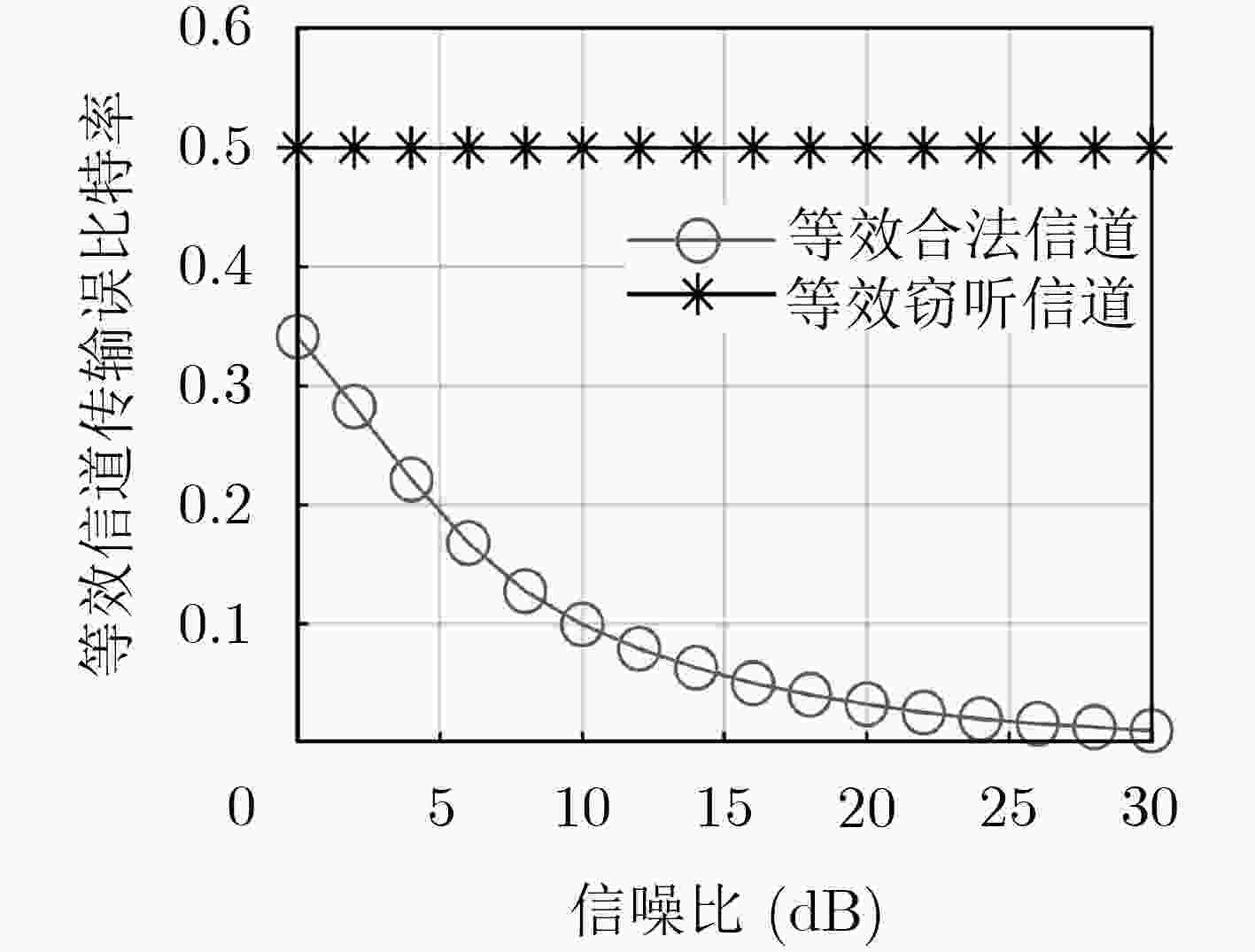
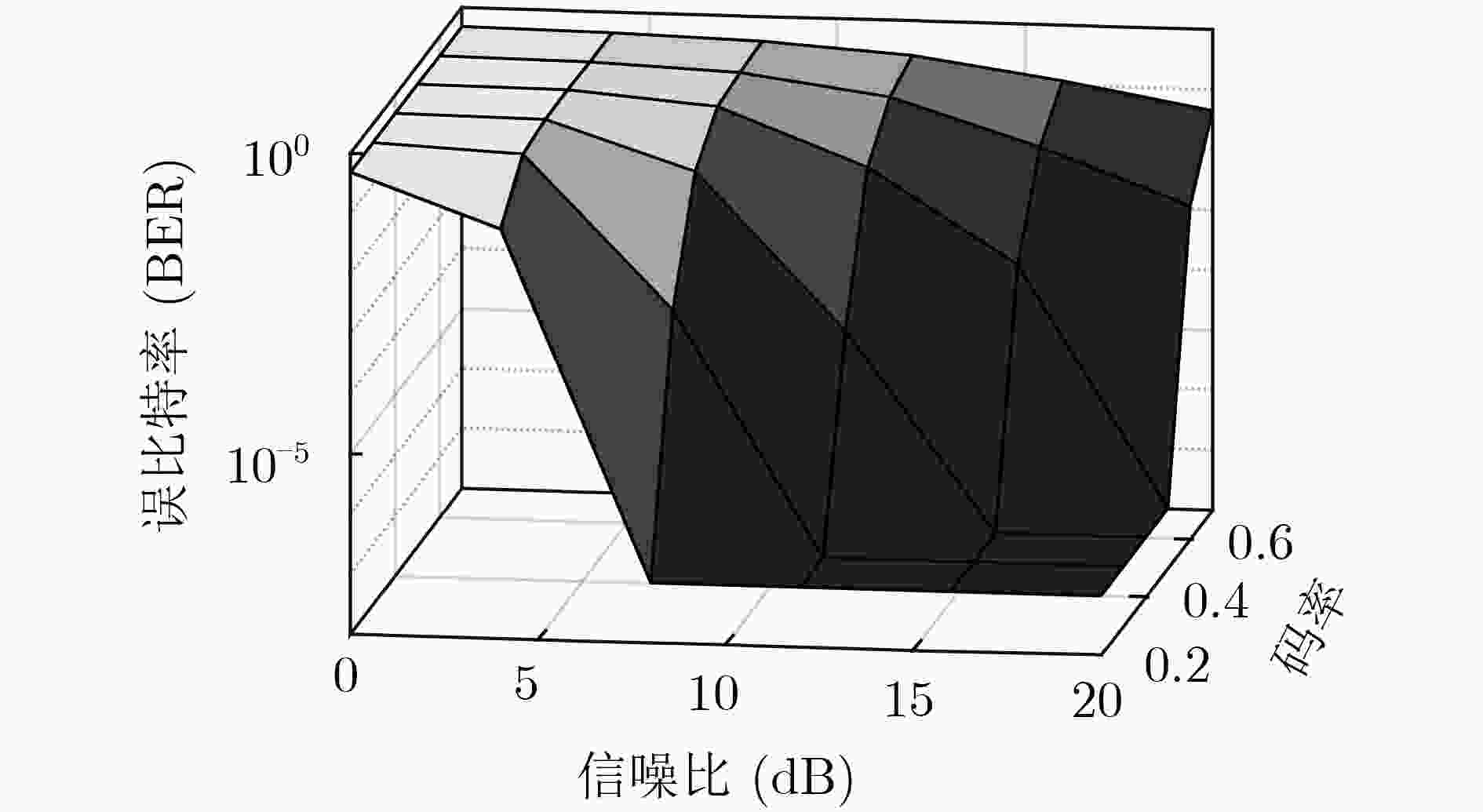
信道条件 极化码设计参数 极化码实际性能 SNR(dB) N K ${P_{{\rm{QoS}}}}$ ${P_{{\rm{Sec}}}}$ $P_{\rm{e}}^{{\rm{AB}}}$ $P_{\rm{e}}^{{\rm{AE}}}$ $2$ $512$ 27 ${10^{ - 6}}$ ${10^{ - 1}}$ $9.2368 \times {10^{ - 7}}$ $0.4865$ $6$ $156$ $2.5952 \times {10^{ - 7}}$ $0.4973$ $10$ $203$ $1.1011 \times {10^{ - 7}}$ $0.4799$ -
JI Xinsheng, HUANG Kaizhi, JIN Liang, et al. Overview of 5G security technology[J]. Science China Information Sciences, 2018, 61(8): 081301. doi: 10.1007/s11432-017-9426-4 JIAO Long, WANG Ning, WANG Pu, et al. Physical layer key generation in 5G wireless networks[J]. IEEE Wireless Communications, 2019, 26(5): 48–54. doi: 10.1109/MWC.001.1900061 WU Yongpeng, KHISTI A, XIAO Chengshan, et al. A survey of physical layer security techniques for 5G wireless networks and challenges ahead[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(4): 679–695. doi: 10.1109/JSAC.2018.2825560 LI Guyue, SUN Chen, ZHANG Junqing, et al. Physical layer key generation in 5G and beyond wireless communications: Challenges and opportunities[J]. Entropy, 2019, 21(5): 497. doi: 10.3390/e21050497 LI Guyue, ZHANG Zheying, Yu Yi, et al. A hybrid information reconciliation method for physical layer key generation[J]. Entropy, 2019, 21(7): 688. doi: 10.3390/e21070688 PENG Linning, LI Guyue, ZHANG Junqing, et al. Securing M2M transmissions using nonreconciled secret keys generated from wireless channels[C]. 2018 IEEE Globecom Workshops, Abu Dhabi, The United Arab Emirates, 2018: 1–6. ASSALINI A, DALL’ANESE E, and PUPOLIN S. Linear MMSE MIMO channel estimation with imperfect channel covariance information[C]. 2009 IEEE International Conference on Communications, Dresden, Germany, 2009: 1–5. HU Xiaoyan, JIN Liang, and ZHONG Zhou. A scrambling scheme based on random wireless channel characteristics for secure transmission[C]. The 2020 12th International Conference on Communication Software and Networks, Chongqing, China, 2020: 29–38. ISLAM N, GRAUR O, FILIP A, et al. LDPC code design aspects for physical-layer key reconciliation[C]. 2015 IEEE Global Communications Conference, San Diego, USA, 2015: 1–7. ARIKAN E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on information Theory, 2009, 55(7): 3051–3073. doi: 10.1109/TIT.2009.2021379 TRIFONOV P. Efficient design and decoding of polar codes[J]. IEEE Transactions on Communications, 2012, 60(11): 3221–3227. doi: 10.1109/TCOMM.2012.081512.110872 张胜军, 钟州, 金梁, 等. 基于安全极化码的密钥协商方法[J]. 电子与信息学报, 2019, 41(6): 1413–1419. doi: 10.11999/JEIT180896ZHANG Shengjun, ZHONG Zhou, JIN Liang, et al. Secret key agreement based on secure polar code[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1413–1419. doi: 10.11999/JEIT180896 ZHANG Shengjun, JIN Liang, HUANG Yu, et al. Nonagreement secret key generation based on spatial symmetric scrambling and secure polar coding[J]. Scientia Sinica Informationis, 2019, 49(4): 486–502. doi: 10.1360/N112018-00119 白慧卿, 金梁, 肖帅芳. 多天线系统中面向物理层安全的极化编码方法[J]. 电子与信息学报, 2017, 39(11): 2587–2593. doi: 10.11999/JEIT170068BAI Huiqing, JIN Liang, XIAO Shuaifang, et al. Polar code for physical layer security in multi-antenna systems[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2587–2593. doi: 10.11999/JEIT170068 Final report of 3GPP TSG RAN WG1 #88bis v1.0. 0[R]. 2017. -





 下载:
下载:



 下载:
下载:
