|
CHUA L. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–509. doi: 10.1109/TCT.1971.1083337
|
|
STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. doi: 10.1038/nature06932
|
|
YALAGALA B, and KHANDELWAL S. Wirelessly destructible MgO-PVP-Graphene composite based flexible transient memristor for security applications[J]. Materials Science in Semiconductor Processing, 2019, 104: 104673. doi: 10.1016/j.mssp.2019.104673
|
|
张刚, 陈和祥, 张天骐. 多用户降噪差分混沌键控通信方案[J]. 电子与信息学报, 2019, 41(2): 362–368. doi: 10.11999/JEIT171173ZHANG Gang, CHEN Hexiang, and ZHANG Tianqi. A multiuser noise reduction differential chaos shift keying system[J]. Journal of Electronics &Information Technology, 2019, 41(2): 362–368. doi: 10.11999/JEIT171173
|
|
ZHANG Weiwei, CAO Jinde, WU Ranchao, et al. Novel results on projective synchronization of fractional-order neural networks with multiple time delays[J]. Chaos, Solitons & Fractals, 2018, 117: 76–83. doi: 10.1016/j.chaos.2018.10.009
|
|
LUNELLI L, COLLINI C, JIMENEZ-GARDUÑO A M, et al. Prototyping a memristive-based device to analyze neuronal excitability[J]. Biophysical Chemistry, 2019, 253: 106212. doi: 10.1016/j.bpc.2019.106212
|
|
闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38(10): 2681–2688.MIN Fuhong, WANG Zhulin, WANG Enrong, et al. New memristor chaotic circuit and its application to image encryption[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2681–2688.
|
|
RAJAGOPAL K, LAAREM G, KARTHIKEYAN A, et al. Fractional order memristor no equilibrium chaotic system with its adaptive sliding mode synchronization and genetically optimized fractional order PID synchronization[J]. Complexity, 2017, 2017: 1892618. doi: 10.1155/2017/1892618
|
|
CHEN Mo, FENG Yang, BAO Han, et al. Hybrid state variable incremental integral for reconstructing extreme multistability in memristive Jerk system with cubic nonlinearity[J]. Complexity, 2019, 2019: 8549472. doi: 10.1155/2019/8549472
|
|
XU Birong, WANG Guangyi, IU H H C, et al. A memristor-meminductor-based chaotic system with abundant dynamical behaviors[J]. Nonlinear Dynamics, 2019, 96(1): 765–788. doi: 10.1007/s11071-019-04820-1
|
|
李志军, 曾以成. 基于文氏振荡器的忆阻混沌电路[J]. 电子与信息学报, 2014, 36(1): 88–93. doi: 10.3724/SP.J.1146.2013.00332LI Zhijun and ZENG Yicheng. A memristor chaotic circuit based on Wien-bridge oscillator[J]. Journal of Electronics &Information Technology, 2014, 36(1): 88–93. doi: 10.3724/SP.J.1146.2013.00332
|
|
RAJAGOPAL K, LI Chunbiao, NAZARIMEHR F, et al. Chaotic dynamics of modified Wien bridge oscillator with fractional order memristor[J]. Radioengineering, 2019, 28(1): 165–174. doi: 10.13164/re.2019.0165
|
|
RUAN Jingya, SUN Kehui, MOU Jun, et al. Fractional-order simplest memristor-based chaotic circuit with new derivative[J]. The European Physical Journal Plus, 2018, 133(1), No.3: 1–12. doi: 10.1140/epjp/i2018-11828-0.
|
|
GUO Zhang, SI Gangquan, XU Xiang, et al. Generalized modeling and character analyzing of composite fractional-order memristors in series connection[J]. Nonlinear Dynamics, 2019, 95(1): 101–115. doi: 10.1007/s11071-018-4553-y
|
|
SI Gangquan, DIAO Lijie, and ZHU Jianwei. Fractional-order charge-controlled memristor: Theoretical analysis and simulation[J]. Nonlinear Dynamics, 2017, 87(4): 2625–2634. doi: 10.1007/s11071-016-3215-1
|
|
YANG Ningning, XU Cheng, WU Chaojun, et al. Fractional-order cubic nonlinear flux-controlled memristor: Theoretical analysis, numerical calculation and circuit simulation[J]. Nonlinear Dynamics, 2019, 97(1): 33–44. doi: 10.1007/s11071-019-04920-y
|
|
YANG Ningning, CHENG Shucan, WU Chaojun, et al. Dynamic behaviors analysis of a chaotic circuit based on a novel fractional-order generalized memristor[J]. Complexity, 2019, 2019: 6083853. doi: 10.1155/2019/6083853
|
|
MOU Jun, SUN Kehui, WANG Huihai, et al. Characteristic analysis of fractional-order 4D hyperchaotic memristive circuit[J]. Mathematical Problems in Engineering, 2017, 2017: 2313768. doi: 10.1155/2017/2313768
|
|
LI Ruihong and HUANG Dongmei. Stability analysis and synchronization application for a 4D fractional-order system with infinite equilibria[J]. Physica Scripta, 2019, 95(1): 015202. doi: 10.1088/1402-4896/ab3ed2
|
|
CHEN Chengjie, CHEN Jingqi, BAO Han, et al. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons[J]. Nonlinear Dynamics, 2019, 95(4): 3385–3399. doi: 10.1007/s11071-019-04762-8
|
|
BAO Han, WANG Ning, BAO Bocheng, et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 57: 264–275. doi: 10.1016/j.cnsns.2017.10.001
|
|
WAN Peng, SUN Dihua, ZHAO Min, et al. Multistability and attraction basins of discrete-time neural networks with nonmonotonic piecewise linear activation functions[J]. Neural Networks, 2020, 122: 231–238. doi: 10.1016/j.neunet.2019.10.005
|
|
CHEN Mo, SUN Mengxia, BAO Han, et al. Flux-charge analysis of two-memristor-based Chua’s circuit: Dimensionality decreasing model for detecting extreme multistability[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 2197–2206. doi: 10.1109/TIE.2019.2907444
|
|
贺少波, 孙克辉, 王会海. 分数阶混沌系统的Adomian分解法求解及其复杂性分析[J]. 物理学报, 2014, 63(3): 030502. doi: 10.7498/aps.63.030502HE Shaobo, SUN Kehui, and WANG Huihai. Solution of the fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analysis[J]. Acta Physica Sinica, 2014, 63(3): 030502. doi: 10.7498/aps.63.030502
|
|
孙克辉, 贺少波, 何毅, 等. 混沌伪随机序列的谱熵复杂性分析[J]. 物理学报, 2013, 62(1): 010501. doi: 10.7498/aps.62.010501SUN Kehui, HE Shaobo, HE Yi, et al. Complexity analysis of chaotic pseudo-random sequences based on spectral entropy algorithm[J]. Acta Physica Sinica, 2013, 62(1): 010501. doi: 10.7498/aps.62.010501
|





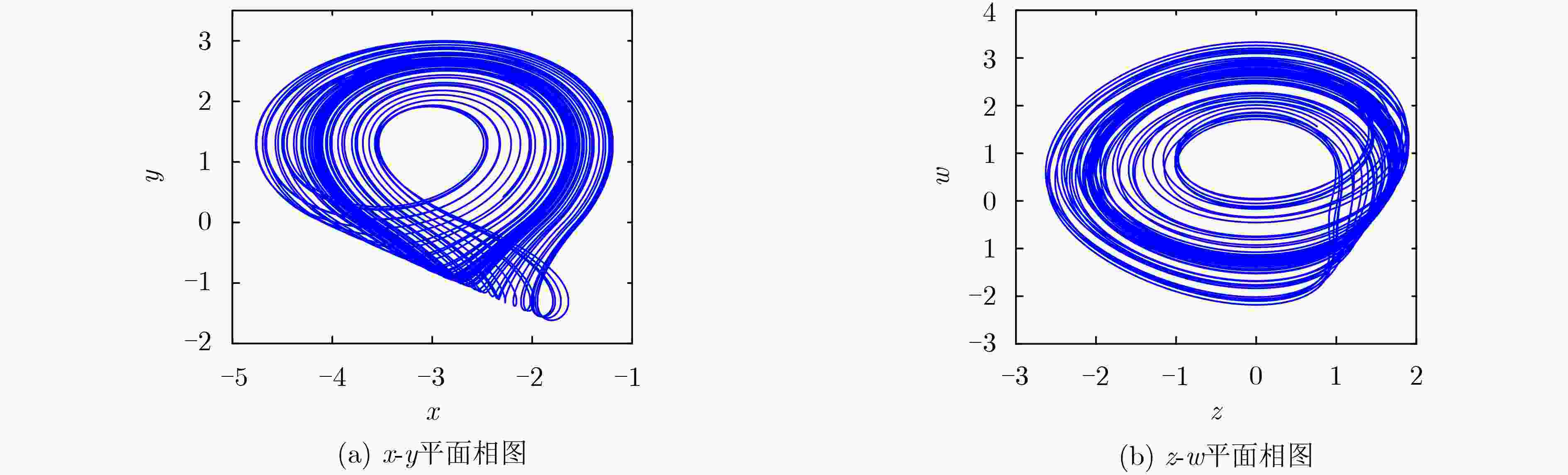
 下载:
下载:
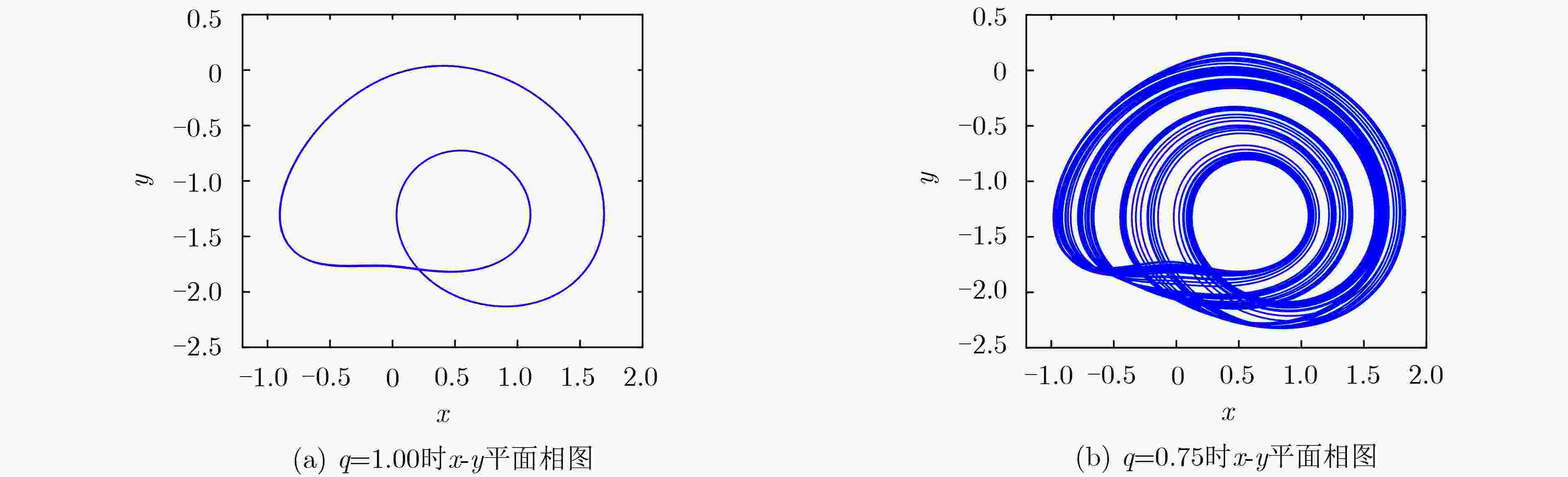
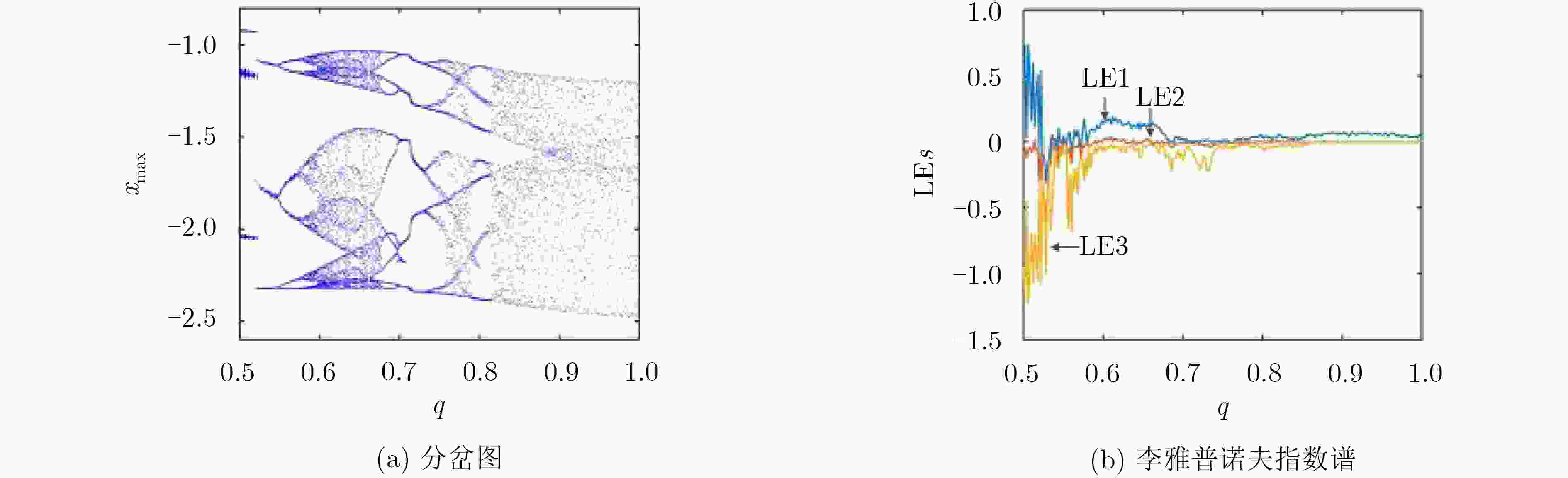
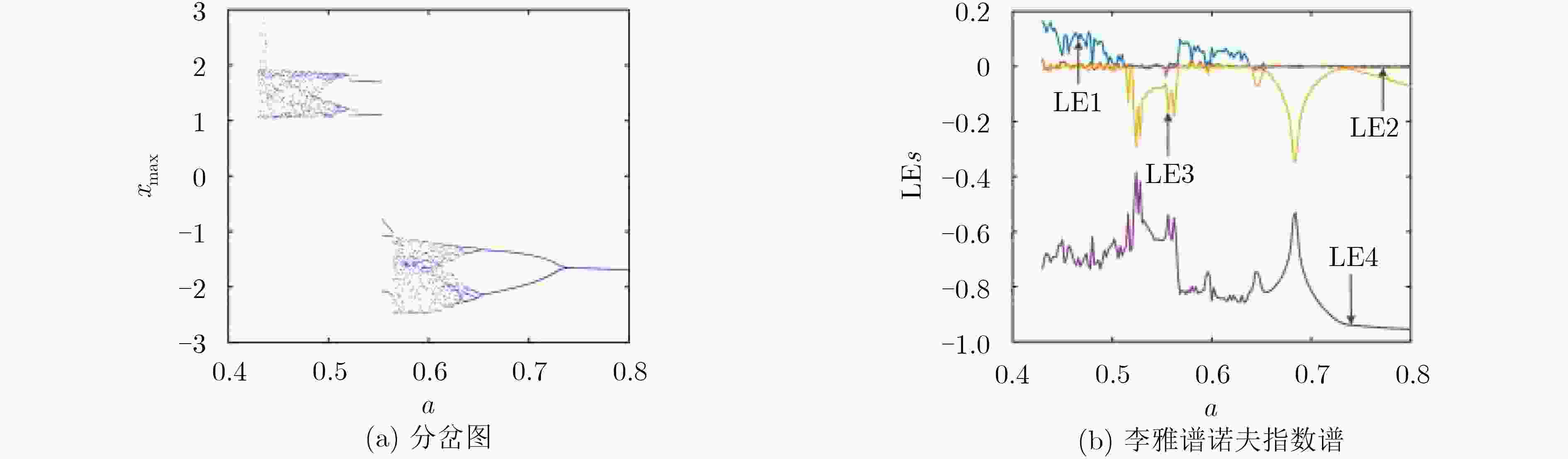


 下载:
下载:
