Construction of Convolution Compressed Sensing Measurement Matrices Based on Cyclotomic Classes
-
摘要:
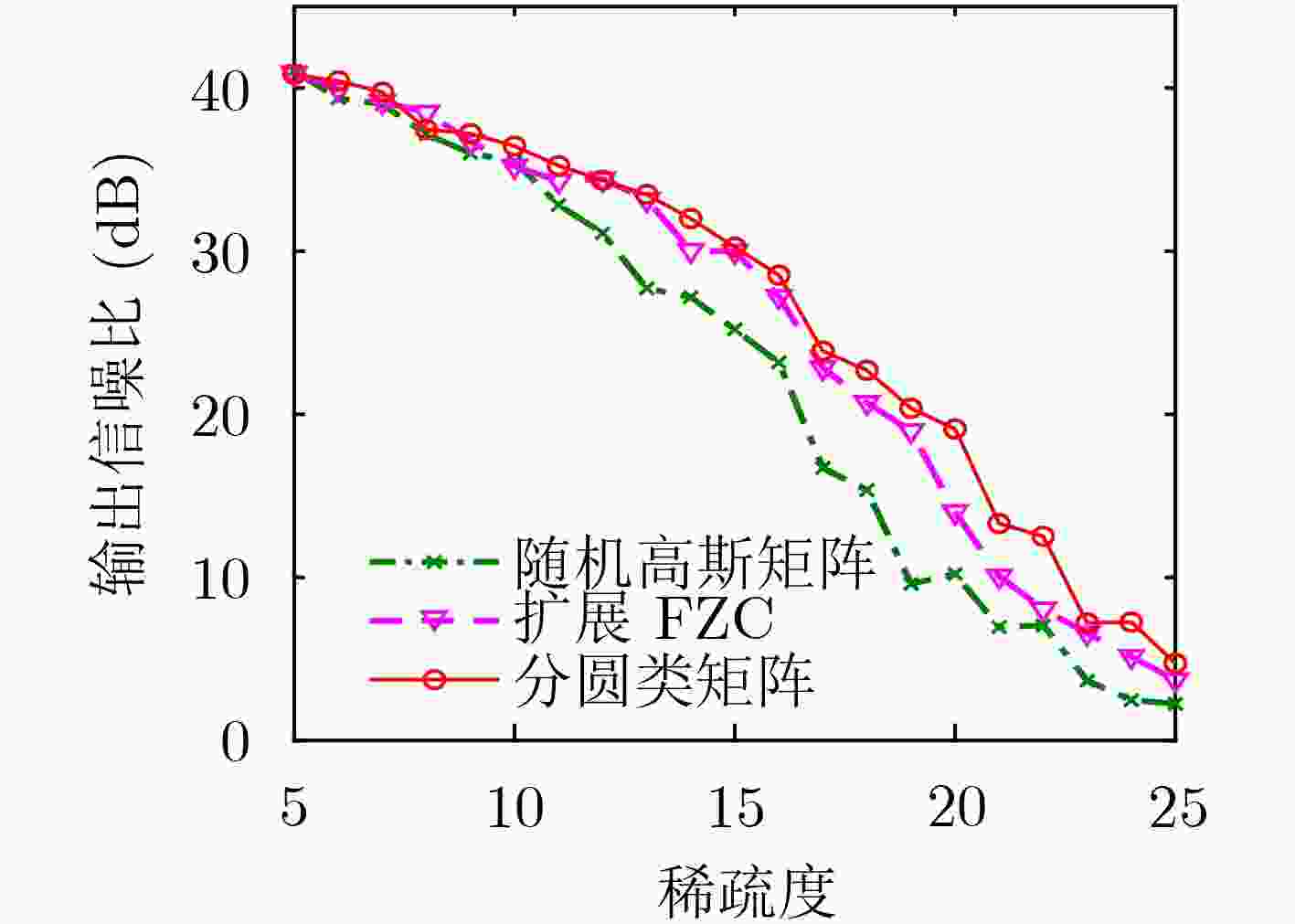
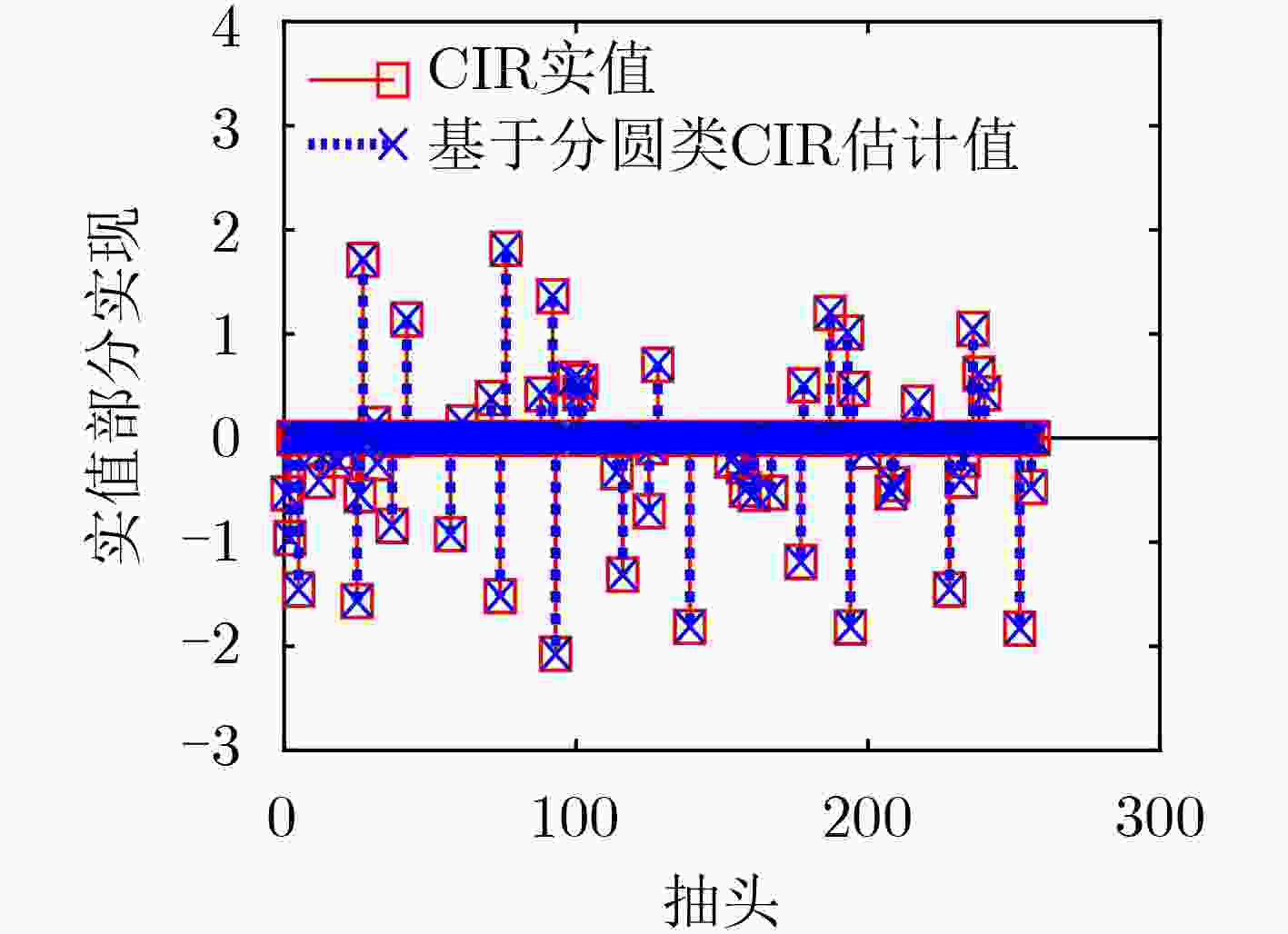
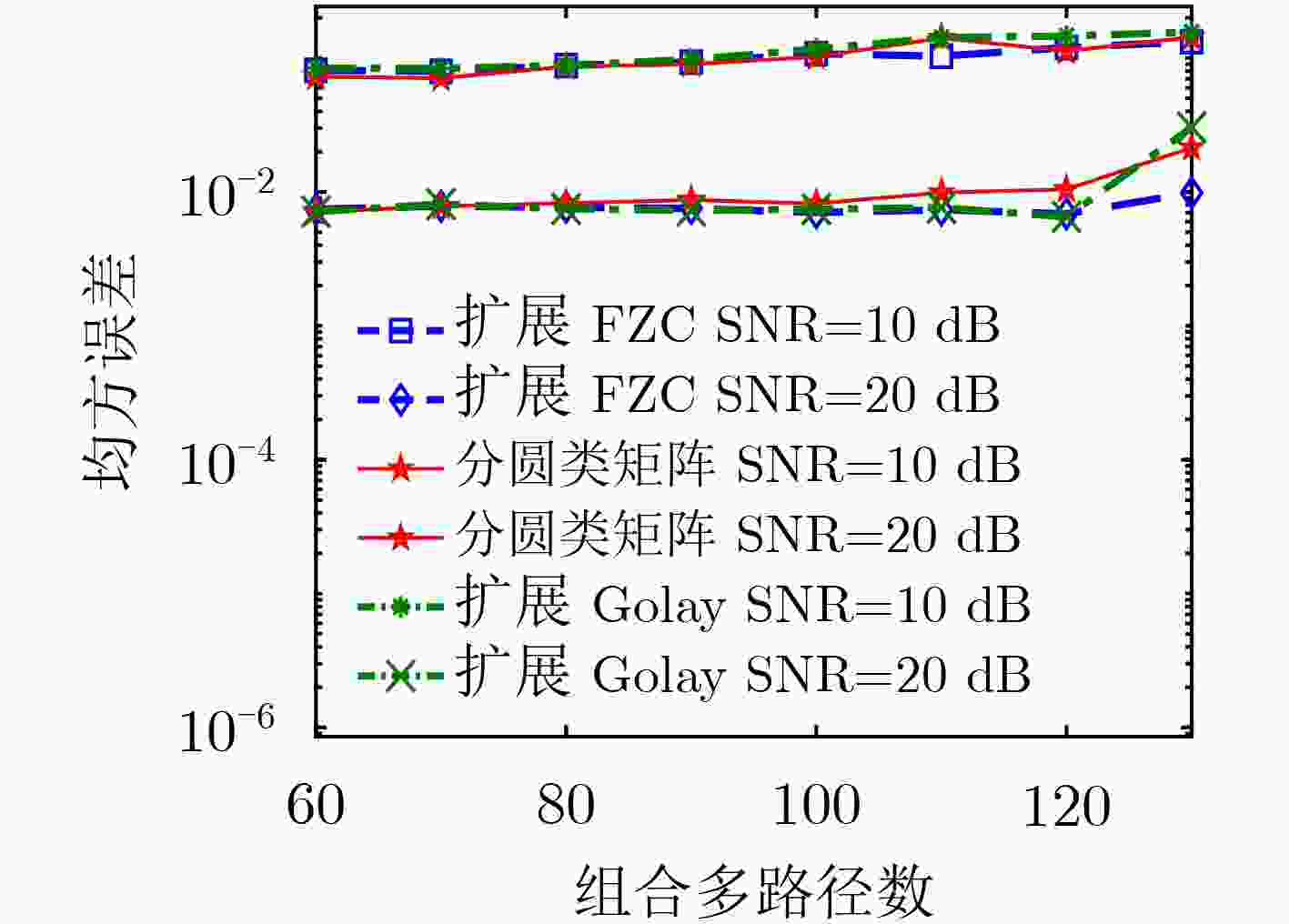
卷积压缩感知是近年来兴起的新型压缩感知技术。卷积压缩感知选用循环矩阵作为测量矩阵,其采样可以简化为卷积的过程,因此大大降低算法复杂度。该文基于分圆类构造适用于卷积压缩感知的测量矩阵,测量值通过利用确定性序列循环卷积信号,然后进行随机2次采样获得。该文构造的测量矩阵的相关性小于已有文献构造的测量矩阵的相关性。模拟仿真结果表明,该文构造的测量矩阵与同等条件下的随机高斯矩阵相比,可以更好地恢复稀疏信号;所构造的矩阵还可以应用于信道估计以及2维图像的重构。
Abstract:Convolutional compressed sensing emerging in recent years is a new type of compressed sensing technology. By using cyclic matrix as measurement matrices, the sampling in convolutional compressed sensing can be simplified into convolution process, thus the complexity of the algorithm is greatly reduced. In this paper, a construction of measurement matrices for convolutional compressed sensing based on cyclotomic classes is proposed. The measurements are obtained by using the circulate convolution signal of the deterministic sequence and then by random subsampling. The correlation of the measurement matrix constructed in this paper is smaller than that of the existing constructions in the literature. The simulation results show that the measurement matrix constructed in this paper can recover the sparse signal better than the random Gaussian matrix under the same conditions. The proposed matrix can also be applied to channel estimation and reconstruction of two-dimensional images.
-
Key words:
- Signal processing /
- Compressed sensing /
- Convolution /
- Cyclotomic class /
- Random sampling
-
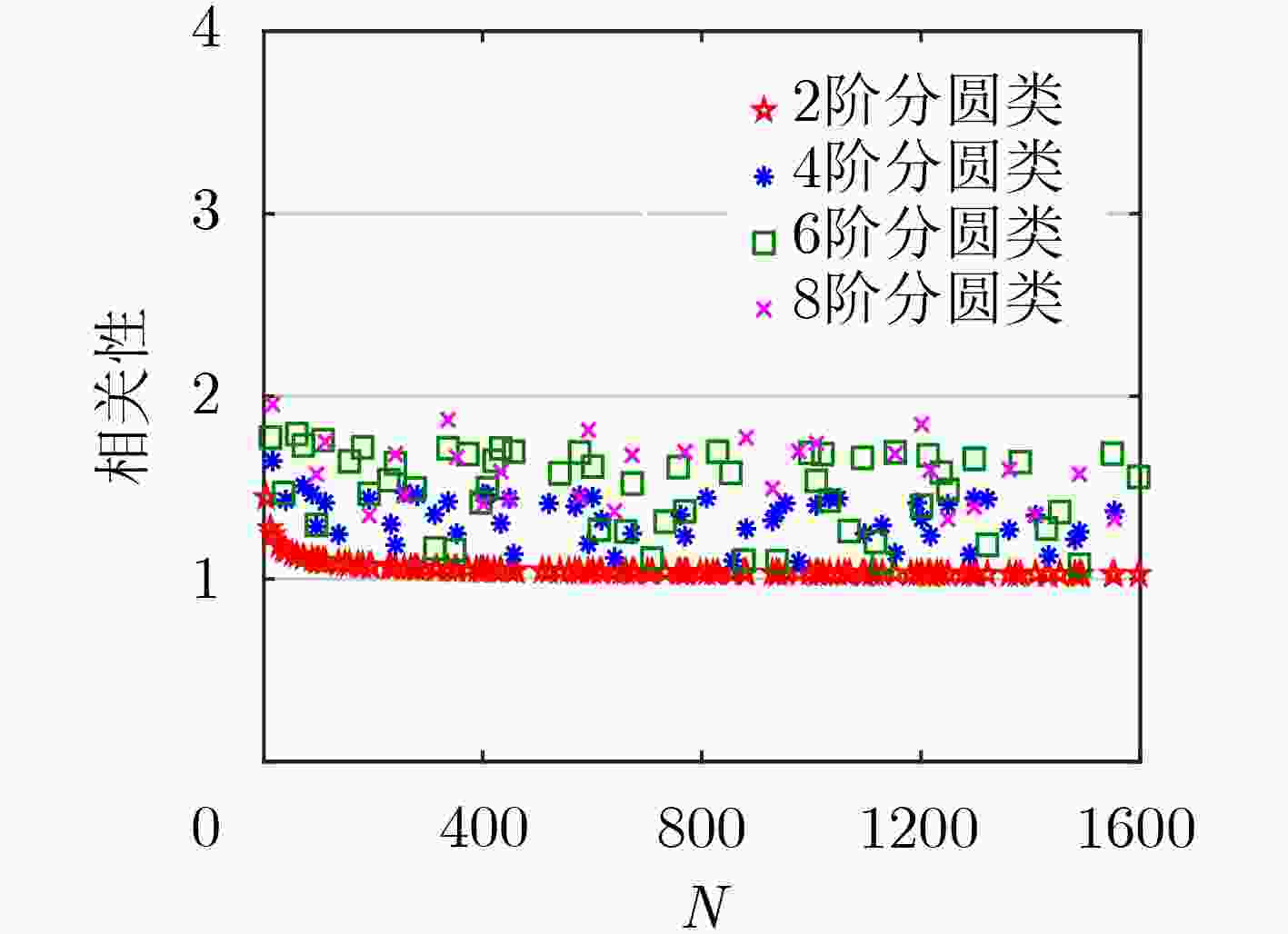
表 1 与已有序列构造的矩阵相关性比较
对角向量$\sigma $ 序列长度$N$ 相关性参数$\mu ({{A}})$ 文献[10] 抽样Sidelnikov序列 $N = \dfrac{ { {p^m} - 1} }{c}$, $c$为偶数 $\sqrt {c + {{\rm{1}} / N}} + {1 / {\sqrt N }}$, $N$为偶数 $\sqrt {c + {1 / N}} $, $N$为奇数 文献[11] Extended Frank-Zadoff-Chu(扩展FZC)序列 $N$为偶数 $4 + {4 / {\sqrt N }}$ $N$为奇数 $2.69 + {{8.15} / {\sqrt N }}$ Extended Golay(扩展Golay)序列 $N = {2^{{k_1}}}{10^{{k_2}}}{26^{{k_3}}}$, $N$为偶数,${k_1},{k_2},{k_3}$为整数 $2 + {2 / {\sqrt N }}$ $N = {2^{{k_1}}}{10^{{k_2}}}{26^{{k_3}}} \pm 1$, $N$为奇数,${k_1},{k_2},{k_3}$为整数 $2 + {1 / {\sqrt N }}$ 本文 由2阶分圆类得到的序列 $N = p$为奇素数,$p \equiv 1({\rm{mod}}4)$ $1 + {1 / {\sqrt N }}$ 由$e > 2$阶分圆类得到的序列 $N = p$为奇素数 $\mu ({{A} }) \le 2$ -
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 DONOHO D L and ELAD M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization[J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(5): 2197–2202. doi: 10.1073/pnas.0437847100 范剑英, 马明阳, 赵首博. 基于压缩感知高反光成像技术研究[J]. 电子与信息学报, 2020, 42(4): 1013–1020. doi: 10.11999/JEIT190512FAN Jianying, MA Mingyang, and ZHAO Shoubo. Research on high reflective imaging technology based on compressed sensing[J]. Journal of Electronics &Information Technology, 2020, 42(4): 1013–1020. doi: 10.11999/JEIT190512 李玮, 邓维波, 杨强, 等. 基于确定性压缩感知采样策略的阵列失效单元远场诊断方法[J]. 电子与信息学报, 2018, 40(11): 2541–2546. doi: 10.11999/JEIT180175LI Wei, DENG Weibo, YANG Qiang, et al. Far-field diagnosis method of array failure cells based on deterministic compressed sensing sampling strategy[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2541–2546. doi: 10.11999/JEIT180175 LI Yubo, XUAN Hongqian, JIA Dongyan, et al. A construction of sparse deterministic measurement matrices[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2019, E102. A(11): 1575–1579. doi: 10.1587/transfun.e102.a.1575 NOUASRIA H and ET-TOLBA M. Sensing matrix based on Kasami codes for compressive sensing[J]. IET Signal Processing, 2018, 12(8): 1064–1072. doi: 10.1049/iet-spr.2017.0537 GU Zhi, ZHOU Zhengchun, YANG Yang, et al. Deterministic compressed sensing matrices from sequences with optimal correlation[J]. IEEE Access, 2019, 7: 16704–16710. doi: 10.1109/ACCESS.2019.2896006 LIU Haiqiang, YIN Jihang, HUA Gang, et al. Deterministic construction of measurement matrices based on Bose balanced incomplete block designs[J]. IEEE Access, 2018, 6: 21710–21718. doi: 10.1109/ACCESS.2018.2824329 CUI Xiang. Construction of deterministic measurements matrix using decimated Legendre sequences[J]. MATEC Web of Conferences, 2015, 22: 01047. doi: 10.1051/matecconf/20152201047 YU N Y and GAN Lu. Convolutional compressed sensing using decimated sidelnikov sequences[J]. IEEE Signal Processing Letters, 2014, 21(5): 591–594. doi: 10.1109/LSP.2014.2311659 LI Kezhi, GAN Lu, and LING Cong. Convolutional compressed sensing using deterministic sequences[J]. IEEE Transactions on Signal Processing, 2013, 61(3): 740–752. doi: 10.1109/TSP.2012.2229994 TROPP J A. Random filters for compressive sampling[C]. The 2006 40th Annual Conference on Information Sciences and Systems, Princeton, USA, 2006: 216–217. doi: 10.1109/CISS.2006.286465. BAJWA W U, HAUPT J D, RAZ G M, et al. Toeplitz-structured compressed sensing matrices[C]. 2007 IEEE/SP 14th Workshop on Statistical Signal Processing, Madison, USA, 2007: 294–298. doi: 10.1109/SSP.2007.4301266. ROMBERG J. Compressive sensing by random convolution[J]. SIAM Journal on Imaging Sciences, 2009, 2(4): 1098–1128. doi: 10.1137/08072975X CANDÈS E J, ROMBERG J K, and TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. doi: 10.1002/cpa.20124 BOURGAIN J, DILWORTH S J, FORD K, et al. Explicit constructions of RIP matrices and related problems[J]. Duke Mathematical Journal, 2011, 159(1): 145–185. doi: 10.1215/00127094-1384809 申颖. 基于分圆类和广义分圆类的几乎差集偶构造方法研究[D]. [硕士论文], 燕山大学, 2016: 1–62.SHEN Ying. The constructions of almost difference set pairs based on cyclotomy and generalized cyclotomy[D]. [Master dissertation], Yanshan University, 2016: 1–62. TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108 YANG Junfeng, ZHANG Yin, and YIN Wotao. A fast alternating direction method for TVL1-L2 signal reconstruction from partial Fourier data[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 288–297. doi: 10.1109/JSTSP.2010.2042333 HALE E T, YIN W, and ZHANG Yin. Fixed-point continuation for ℓ1-minimization: Methodology and convergence[J]. SIAM Journal on Optimization, 2008, 19(3): 1107–1130. doi: 10.1137/070698920 -





 下载:
下载:



 下载:
下载:
