Micro-motion Gesture Recognition Based on Multi-channel Frequency Modulated Continuous Wave Millimeter Wave Radar
-
摘要:
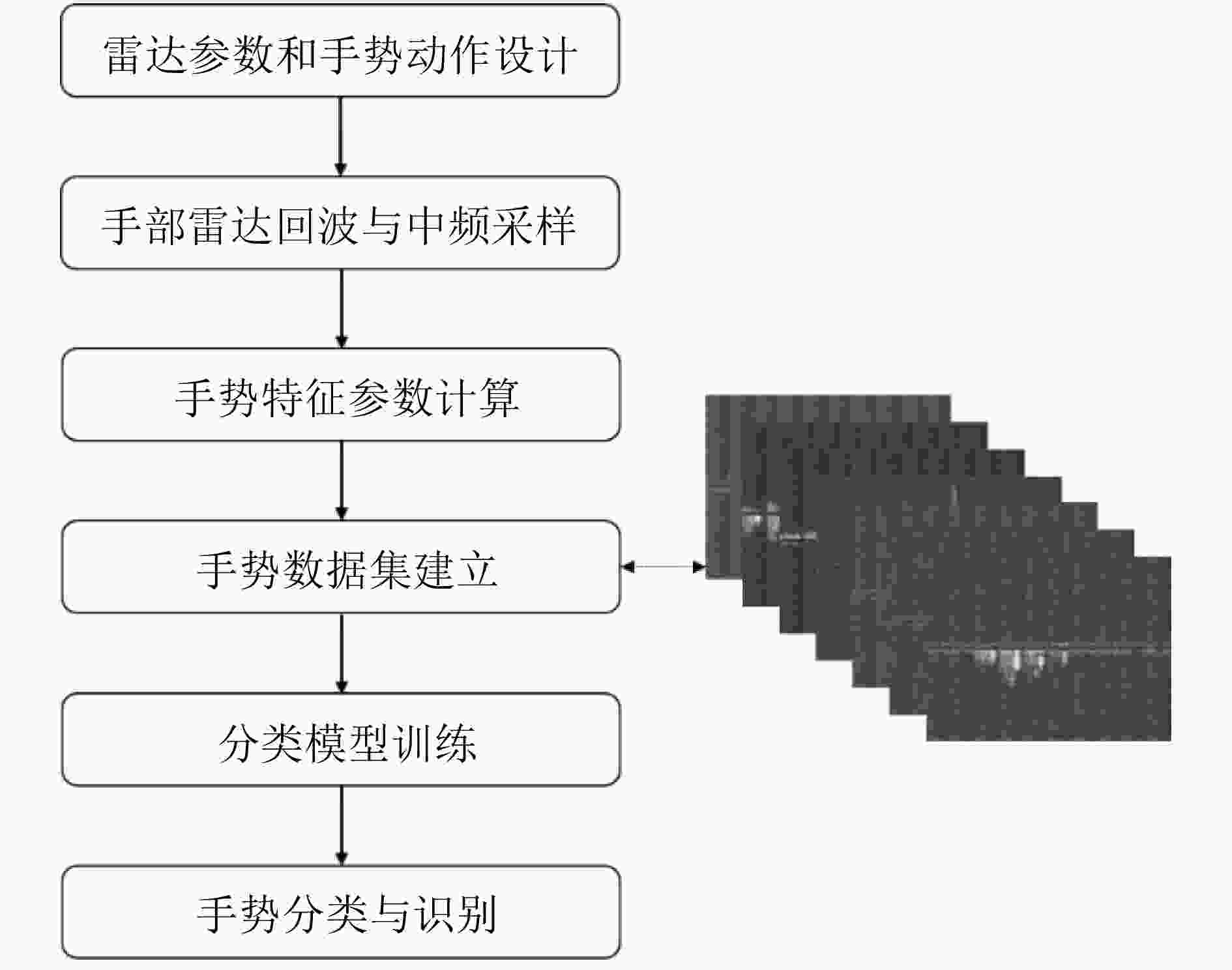
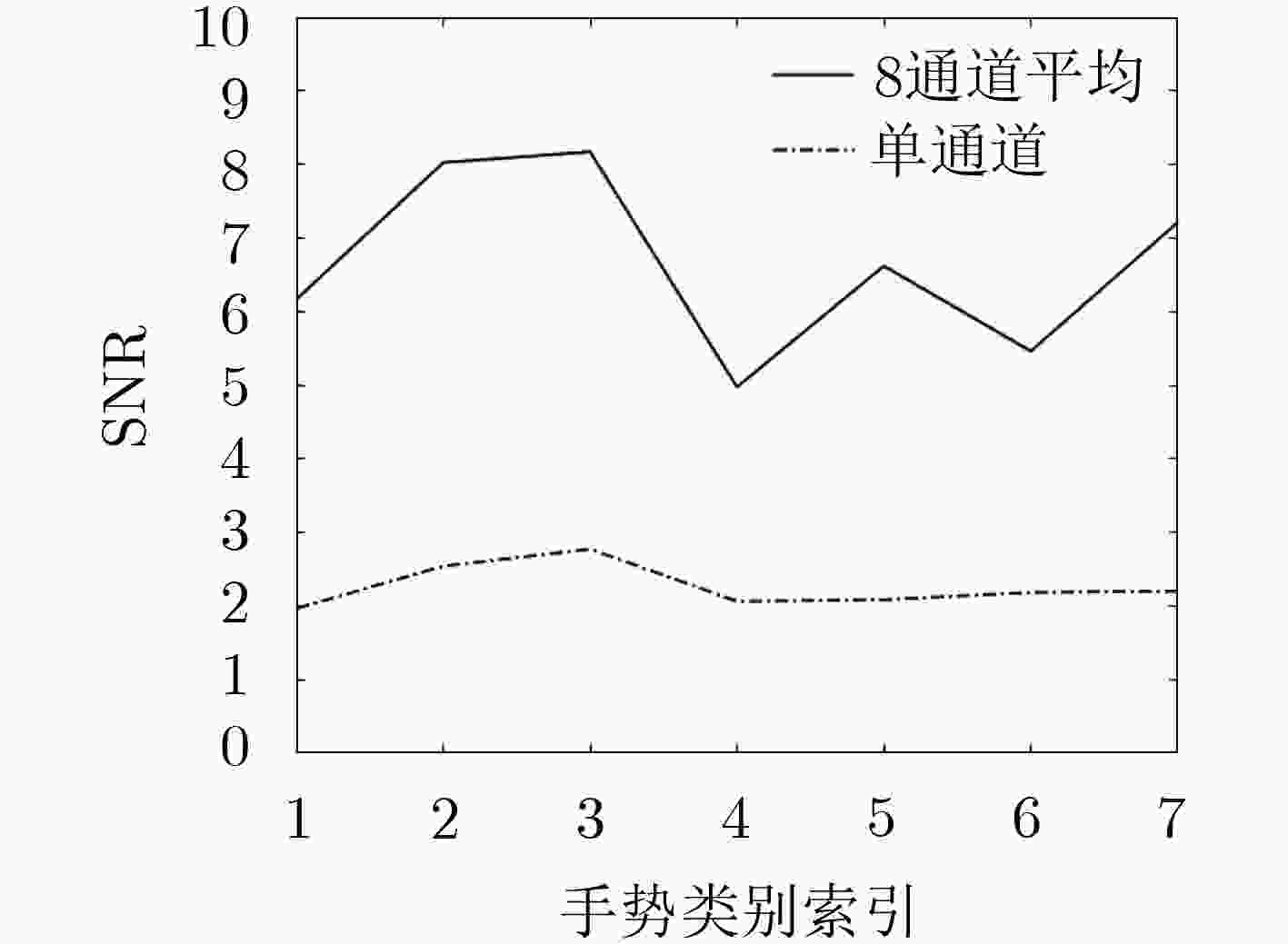
该文提出一种基于多通道调频连续波(FMCW)毫米波雷达的微动手势识别方法，并给出一种微动手势特征提取的最优雷达参数设计准则。通过对手部反射的雷达回波进行时频分析处理，估计目标的距离多普勒谱、距离谱、多普勒谱和水平方向角度谱。设计固定帧时间长度拼接的距离-多普勒-时间图特征，与距离-时间特征、多普勒-时间特征、水平方向角度-时间图特征和三者联合特征等，分别对7类微动手势进行表征。根据手势运动过程振幅和速度差异，进行手势特征捕获和对齐。利用仅有5层的轻量化卷积神经网络对微动手势特征进行分类。实验结果表明，相较其他特征，设计的距离-多普勒-时间图特征能够更为准确地表征微动手势，且对未经训练的测试对象具有更好的泛化能力。
Abstract:A micro-motion gesture recognition method based on multi-channel Frequency Modulated Continuous Wave (FMCW) millimeter wave radar is proposed, and an optimal radar parameter design criterion for feature extraction of micro-motion gestures is presented. The time-frequency analysis process is performed on the radar echo reflected by the hand, and the range Doppler spectrum, the range spectrum, the Doppler spectrum and the horizontal direction angle spectrum of the target are estimated. Then the range-Doppler-time-map feature is designed, range-time-map feature, Doppler-time-map feature, horizontal-angle-time-map feature, and three-joint feature with fixed frame time length are used to characterize the 7 classes micro-motion gestures, respectively. And these gesture features are captured and aligned according to the difference in amplitude and speed of the gesture motion process. Then a five-layer lightweight convolutional neural network is designed to classify the gesture features. The experimental results show that, the range-Doppler-time-map feature designed in this paper characterizes the micro-motion gesture more accurately and has a better generalization ability for untrained test objects compared with other features.
-
1. 引言
手势识别技术在人机交互领域具有重要的应用价值，可用于智能家居[1]、智能驾驶[2]、VR[3]、手语实时翻译[4]、游戏控制[5]等多种应用场景。
现有的手势识别方法主要包括基于穿戴式传感器[4]，基于可见光[6]、红外[7]、深度[8]等视觉图像，基于超声波[9]，基于TV[10], RFID[10,11], Wi-Fi[12]等非宽带无线通信信号和基于雷达5种。其中穿戴式传感器方法要求人体携带设备，适用场景有限；视觉图像方法受光照条件影响明显，且存在泄露用户隐私的风险；超声波方法受传播速度和衍射影响明显；非宽带无线通信信号方法分辨率低，难以滤除背景干扰。
基于雷达的手势识别方法主要采用连续波多普勒雷达[13]、脉冲超宽带雷达[2]和调频连续波(Frequency Modulated Continuous Wave, FMCW)雷达[14-19]3种雷达体制。其中连续波多普勒雷达抗干扰能力差，且雷达带宽较小，距离向分辨率低，无法通过信号处理的手段滤除距离向干扰。脉冲超宽带雷达利用目标回波信号与发射信号之间的时间差测量距离，相比FMCW雷达，精确的时间差测量、信号调制和信号处理等过程对系统硬件性能要求较高，因此成本较高。
近年来，随着FMCW毫米波雷达芯片的大规模商用，FMCW毫米波雷达在手势识别技术上的应用潜力引起了关注。FMCW雷达的优势在于硬件成本低，测距、测速方案简单，抗干扰能力强，而高频率大带宽的毫米波能够带来更好的速度分辨率和距离分辨率。2015年，谷歌公开演示了利用60 GHz频段FMCW毫米波雷达芯片实现近距离微动手势识别的Soli[14-16]项目。Soli团队采用基于多达七百多种特征的随机森林方法[14]和基于距离多普勒特征的端到端卷积循环神经网络方法[15]进行手势分类，分别能够实现4种微动手势92.1%和11种中小运动幅度手势87%的平均分类准确率。Soli的芯片供应商英飞凌采用基于序列的距离多普勒特征图像训练的长循环全卷积神经网络方法[16]进行手势识别，能够实现5种微动手势94.34%的平均分类准确率。德州仪器公司基于自研77 GHz频段毫米波雷达芯片，利用隐马尔可夫方法[17]能够实现6种中等运动幅度手势83.3%的平均分类准确率。文献[18]中采用基于手势动作的距离、多普勒和角度多维参数特征进行卷积神经网络分类的方法，能够实现6种大运动幅度手势95.3%的平均分类准确率。
然而，现有的基于FMCW毫米波雷达的手势识别方法主要侧重于分类特征的融合或分类方法的研究，未对雷达参数设计和手势特征表征能力对分类的影响进行深入研究，仍然存在手势特征不能有效融合、难以表征微动手势的问题。例如，文献[14]采用过多的手势特征进行组合，一些较差的手势特征容易导致最终的手势表征能力变差；文献[15,16]中采用原始的距离多普勒特征，文献[17]中采用速度能量分布特征，均不足以准确表征类别较多、存在相似特征的多种手势动作；文献[18]中采用距离谱、多普勒谱和角度谱联合的多维参数特征，其中距离谱和角度谱难以准确表征距离、角度变化不明显的微动手势，因而与多普勒谱特征联合后表征能力反而变差，仅适用于运动幅度较大的手势表征。
针对上述问题，本文提出基于多通道FMCW毫米波雷达的微动手势识别方法，设计固定帧时间长度的距离多普勒振幅分布拼接特征，通过最优雷达参数设计实现高速度分辨率，从而能够有效表征微动手势，并通过多通道距离多普勒谱非相干叠加平均，获得信噪比明显提升的距离-多普勒-时间图特征。
2. 原理与方法
本文所提基于多通道FMCW毫米波雷达的微动手势识别方法，主要包括雷达最优参数设计、手势特征提取、手势数据集构建和卷积神经网络(Convolutional Neural Network, CNN)结构设计4个部分。其中，雷达最优参数设计部分阐述了如何设计合适的雷达参数，从而能够准确表征微动手势；手势特征提取部分阐述了从雷达回波中获得距离多普勒谱、距离谱、多普勒谱和角度谱的过程；手势数据集构建部分阐述了构造手势特征图像和构建特征图像数据集的过程；CNN结构设计部分阐述了针对雷达手势特征图像设计的轻量化卷积神经网络的主要结构。
2.1 最优雷达参数设计
为了能够对微小的手势动作进行表征，需要进行合适的雷达参数设计，这里给出一种利用FMCW雷达提取微动手势特征的最优雷达参数设计准则。
雷达参数主要包括发射天线数
NTx 、接收天线数NRx 、调频起始频率f1 、调频斜率Ks 、调频周期Tc 、每帧调频周期数Nchirp 、帧周期Tf 、一个周期ADC采样点数Nadc 、ADC采样周期Tadc 、ADC采样率Fs 等，这些参数由应用场景的最大测量距离dmax 、距离分辨率dres 、最大测量速度vmax 、速度分辨率vres 与帧率frate 等主要指标来确定，几种指标分别满足公式dmax=Nadc×dres (1) dres=c2B (2) vmax=λ4Tc (3) vres=λ2Nchirp⋅Tc (4) frate=1Tf (5) 其中，c为光速，
λ 为调频中心频率对应波长，B为有效调频带宽，B由调频斜率Ks 和ADC采样周期Tadc 共同确定B=Ks×Tadc=Ks×NadcFs (6) λ 由调频起始频率f1 和调频带宽B共同确定λ=c(f1+B2) (7) 调频周期
Tc 可以用来调节最大测量速度vmax 和速度分辨率vres ，需要满足Tc=NadcFs+τc−idle (8) 其中，
τc−idle 为发射1个周期扫频信号后的空闲时间。帧周期
Tf 可以用来调节帧率frate ，需要满足Tf=Nchirp×Tc+τf−idle (9) 其中，
τf−idle 为发射Nchirp 个周期扫频信号后的空闲时间。对于采用时分复用(Time Division Multiplexing, TDM)的多发多收(Multiple Input Multiple Output, MIMO)方式，帧周期
Tf 需要满足Tf=NTx×Nchirp×Tc+τf−idle (10) 通常将雷达硬件支持的参数上限作为雷达参数设计的先决条件，与手势识别应用相关的毫米波雷达参数上限包括发射功率决定的最大测量距离
dm−max ，天线设计决定的水平及垂直方向最大视场角θFOV 与虚拟通道数Nchan−H 和Nchan−V ，最大扫频带宽Bmax ，最大调频斜率Ks−max ，最小调频斜率Ks−min ，最大ADC采样率Fs−max 与最小ADC采样率Fs−min 等。在对
dres 要求较高的应用场景中，应使dres 尽可能小，根据式(2)，需要B 尽可能大，根据式(6)，B由Ks ，Nadc 和Fs 共同确定。在
dres 确定后，根据式(1)，Nadc 可以由dmax 确定，偏小会导致远距离的手势动作捕捉不到，偏大会导致多余的原始数据内存占用开销。Ks 与Fs 可以由式(6)和式(8)共同确定，但同时要满足Fs−min≤Fs≤Fs−max 和Ks−min≤Ks≤Ks−max 的条件。人的手势有运动速度上限，如果调频周期
Tc 设置不合理，vmax 偏小会导致速度模糊，vmax 偏大会导致vres=2vmax/Nchirp 偏大，根据式(8)和式(10)，设计准则为：在满足目标最大运动速度测量需求的前提下，使得vres 尽可能小，从而能够捕捉更细微的手势，但同时也要考虑Nchirp 可能影响的帧率大小；根据式(5),
Tf 的大小决定了得到距离多普勒图的帧率，从而决定了对微动手势的时间分辨率，帧率越高，手势能够被帧周期划分得更精细，但Tf 的设置同时也要考虑硬件的实时处理能力，即需要数据处理设备能够在一个帧周期内完成雷达数据处理、特征提取和手势分类的全过程运算。2.2 手势特征提取
在一个调频周期内，雷达发射的FMCW信号可以表示为
sT(tf)=ATexp[−j2π(fctf+∫tf0Kτdτ)] (11) 其中，
tf 表示一个调频周期内的快时间索引，AT 表示发射信号振幅，fc 表示信号中心频率，K表示信号调频斜率，K=B/Tc , B表示信号调频带宽，Tc 表示信号调频周期，Kτ 表示τ 时刻的发射信号频率。经目标场景反射后雷达接收的FMCW信号可以表示为
sR(tf)=ARexp{−j2π[fc(tf−Δtf)+∫tf0[K(τ−Δtf)+Δfd]dτ]} (12) 其中，
AR 表示接收信号振幅，Δtf 表示信号飞行时间，Δtf=2R/c , R表示目标相对雷达的径向距离，c表示光速，K(τ−Δtf) 表示τ 时刻接收信号频率，Δfd 表示多普勒频移。将目标场景反射的回波信号与发射信号进行混频和低通滤波可以得到中频信号，近似为
sIF(tf)=sT(tf)sR(tf)=ATARexp{j2π[fcΔtf+(fIF−Δfd)tf]} (13) 其中，
fIF=KΔtf 表示tf 时刻中频信号的频率。由于
fIFΔtf=BTc=K ，可将目标距离表示为R=cTcfIF2B (14) 另外，中频信号的相位可表示为
φ=2π[fcΔtf+(fIF−Δfd)tf] (15) 由于时延
Δtf 非常小，可忽略式(15)中第1项fcΔtf 的影响，而第2项中fIF 仅与调频周期内的采样点索引n有关，由于Tc 很小，通常假定一个调频周期内多普勒频移是恒定的，则Δfd 仅与调频周期的索引m有关，从而可将一个调频周期序列即一帧内多个调频周期的中频信号离散表示为sIF(n,m)=AIF(n,m)⋅exp{j2π[fIF(n)−Δfd(m)]n/Fs} (16) 其中，
AIF(n,m) 表示中频信号的振幅，Fs 表示中频信号的模拟数字转换(Analog Digital Conversion, ADC)采样率。因此，可通过对任一调频周期m对应的时域中频采样信号做快速傅里叶变换(Fast Fourier Transform, FFT)得到与目标距离相关的中频信号频率分布
fIF(n) (n=1,2,···,Nadc )，也可通过对任一采样点n对应的一个调频周期序列做FFT得到与目标速度相关的多普勒频移分布Δfd(m) (m=1,2,···,Nchirp )，其中Nadc=Fs⋅Tc 为每调频周期采样数，Nchirp 为每帧调频周期数。对一个帧周期内
Nchirp 个调频周期的Nadc 个中频信号采样点数据分别做距离FFT和多普勒FFT后即可得到帧时间即慢时间tslow 时刻目标场景的距离多普勒谱分布。对距离多普勒谱分布做恒虚警率(Constant False Alarm Rate, CFAR)检测可以得到单个目标的距离索引和速度索引，分别将目标距离索引对应的多普勒分布和目标速度索引对应的距离分布按帧时间拼接，可以得到多普勒谱和距离谱，将多个水平或垂直方向虚拟通道、同一距离索引和速度索引对应的复振幅组合，做角度FFT可以得到水平或垂直方向角度分布，将其按帧时间拼接，可以得到水平或垂直方向角度谱。
2.3 手势数据集构建
为了构建包含距离、速度和角度信息的手势数据集，在雷达视场角范围内做预设计的手势动作，对接收到的雷达回波数据进行2.2节中的处理。为了能够实时捕捉完整的手势，设计帧时间长度为
Nf 的滑动帧窗，对应观测时长大于所设计手势动作时长，将角度谱、单通道距离多普勒谱、通道平均距离多普勒谱、通道平均距离谱和通道平均多普勒谱分别送入滑动窗，当帧窗填充满时，滑动窗中前Nf−1 帧的数据被前一帧时刻后Nf−1 帧的数据替换，最后一帧填充新的数据；设定振幅阈值和速度阈值，进行动作帧判定，进而进行滑动帧窗内的特征分割，确定特征的开始帧和结束帧，捕获超过阈值的完整手势特征，并将手势特征对齐到滑动窗的中央位置，然后保存当前帧窗内的特征分布，并清空当前帧窗内数据；重复多次以上过程，保存多个人、多类手势的多组手势特征数据，建立多种手势特征对应的数据集，用于手势分类模型的训练。由于毫米波雷达的阵元间距小，天线阵列集中在一个很小的区域，各个数据通道获得的距离与多普勒特征基本一致，而背景噪声是呈随机分布的，可以通过多通道非相干叠加平均来抑制距离与多普勒特征的背景噪声，提高手势特征的信噪比。
手势特征的帧窗长度设置需要综合考虑所设计手势动作的时间长度和实时性选取，如果帧窗长度偏短，无法完整捕捉持续时间长或有些对象做的慢的手势动作，如果帧窗长度太长，得到一次手势特征的时间较长，不利于实时手势识别的应用。
2.4 卷积神经网络结构设计
根据雷达特征图像的像素尺寸较小、特征区域呈上下或左右对称分布等特点，设计了仅包含5层的轻量化卷积神经网络结构，包括3个2维卷积层，每一卷积层后分别连接1个RELU激活函数层、1个批标准化层和 1个池化层；后接2个全连接层，第1个全连接层连接1个dropout层，第2个全连接层连接第4个RELU激活函数层；最后是softmax层，用于输出分类结果和相似度分布数组。
3. 实验与结果分析
3.1 实验环境
实验采用的多通道FMCW毫米波雷达设备为TI公司的AWR1642-BOOST开发板，支持77～81 GHz最大4 GHz的调频带宽，水平和垂直方向视场角均为±60°，支持最多2个发射天线和4个接收天线。采用TI公司的DCA1000高速数据采集卡获取毫米波雷达芯片输出的中频信号采样数据，并经由以太网传输到戴尔OptiPlex 7010 Mino Tower台式机上(Windows10 64位操作系统，Inter® CoreTM i7-3370 4核CPU@3.40 GHz, 16 GB内存，2 GB显存NVIDIA GeForce GTX 760显卡)，在MATLAB 2018b中进行数据处理以及CNN训练与分类。实验使用2发4收的天线阵列以时分复用的MIMO方式构成1维虚拟天线阵列，包含8个数据通道。雷达主要参数设置为特征帧长10，每帧Chirp数128，每个Chirp采样点数64，调频频率范围77～81 GHz，实验流程如图1所示。
3.2 构建手势数据集
设计如图2所示的食指双击、食指顺时针绕圈、食指逆时针绕圈、食指拇指分开、食指拇指并拢、拇指在食指上前搓动和拇指在食指上后搓动等7类手部整体不发生明显平移、仅有手指运动的微动手势。由7名实验人员分别在距离雷达0.5 m以内，雷达视场角范围内的不同3维空间位置做指定手势动作，根据2.2节和2.3节的过程获取7类微动手势对应各50组如图2所示的单通道距离-多普勒-时间图(Single Channel Range-Doppler-Time-Map, SC-RDTM)、通道平均距离-多普勒-时间图(Channel Average Range-Doppler-Time-Map, CA-RDTM)、通道平均多普勒-时间图(Channel Average Doppler-Time-Map, CA-DTM)、通道平均距离-时间图(Channel Average Range-Time-Map, CA-RTM)、水平方向角度-时间图(Horizontal-Angle-Time-Map, HATM)等5种手势特征图像(缩放为64×64大小后)，每种手势特征对应7人×7类×50张图像样本构成的手势数据集。
3.3 训练与分类
根据输入手势特征图像的通道数，将CNN的图像输入层尺寸设置为64×64×1或64×64×3，输入的特征图像需要被进行缩放，缩放后的手势特征图像如图2所示，为了弥补手势特征在图像水平方向的位置差异，设置水平方向左移5个像素到右移5个像素的数据增强，采用动量梯度下降优化器，0.001的恒定学习率，迭代20个Epochs，每次迭代的批样本数(batch size)为64，每个Epoch迭代次数为112，采用GPU加速训练，在训练过程中进行测试集的验证，每迭代50次测试一次数据集，一次完整的训练和测试过程需要耗时3 min左右。
为了验证手势特征中帧窗长度对手势识别性能的影响，分别获取6帧、8帧、10帧和15帧时间长度，5名实验对象7类微动手势各50组的CA-RDTM特征对应的手势特征数据集，利用相同的单通道CNN方法进行训练和测试，训练测试比为6:4，准确率对比如表1所示，可以看出少于10帧的数据集由于不能完整捕捉部分手势，分类表现较差，而15帧的数据集相比10帧的数据集，虽然帧数增加了5帧，分类准确率并没有明显的提升，在带来更大的内存开销的同时也会影响实时性，因此本文选择10帧时间长度来表征7种微动手势。
表 1 不同时间长度特征的分类准确率对比(%)数据集长度 6帧 8帧 10帧 15帧 平均分类准确率 76.86 91.86 99.14 99.29 3.4 多种手势表征方法对比
为了比较不同分类特征的手势表征能力，分别将SC-RDTM, CA-RDTM, CA-DTM, CA-RTM, HATM以及RTM, DTM与HATM联合作为手势特征，进行CNN训练与测试，其中RTM, DTM与HATM联合的多维参数特征的CNN输入层大小设置为64×64×3, 3个通道分别对应CA-RTM, CA-DTM与HATM 3 种特征。
首先将7名实验对象的手势数据集按实验对象划分为5:2的比例，其中5名实验对象作为训练对象，另外2名实验对象作为测试对象，之后将5名训练对象的手势数据集按照6:4的比例分成训练集和测试集，每类训练样本数150，每类测试样本数100，共计1050个训练样本和700个测试样本，顺序被随机打乱后输入卷积神经网络进行训练和测试，对6种手势特征对应的7类微动手势的平均分类准确率如表2所示。
表 2 多种手势表征方法的对比特征类型 分类方法 5名训练对象平均
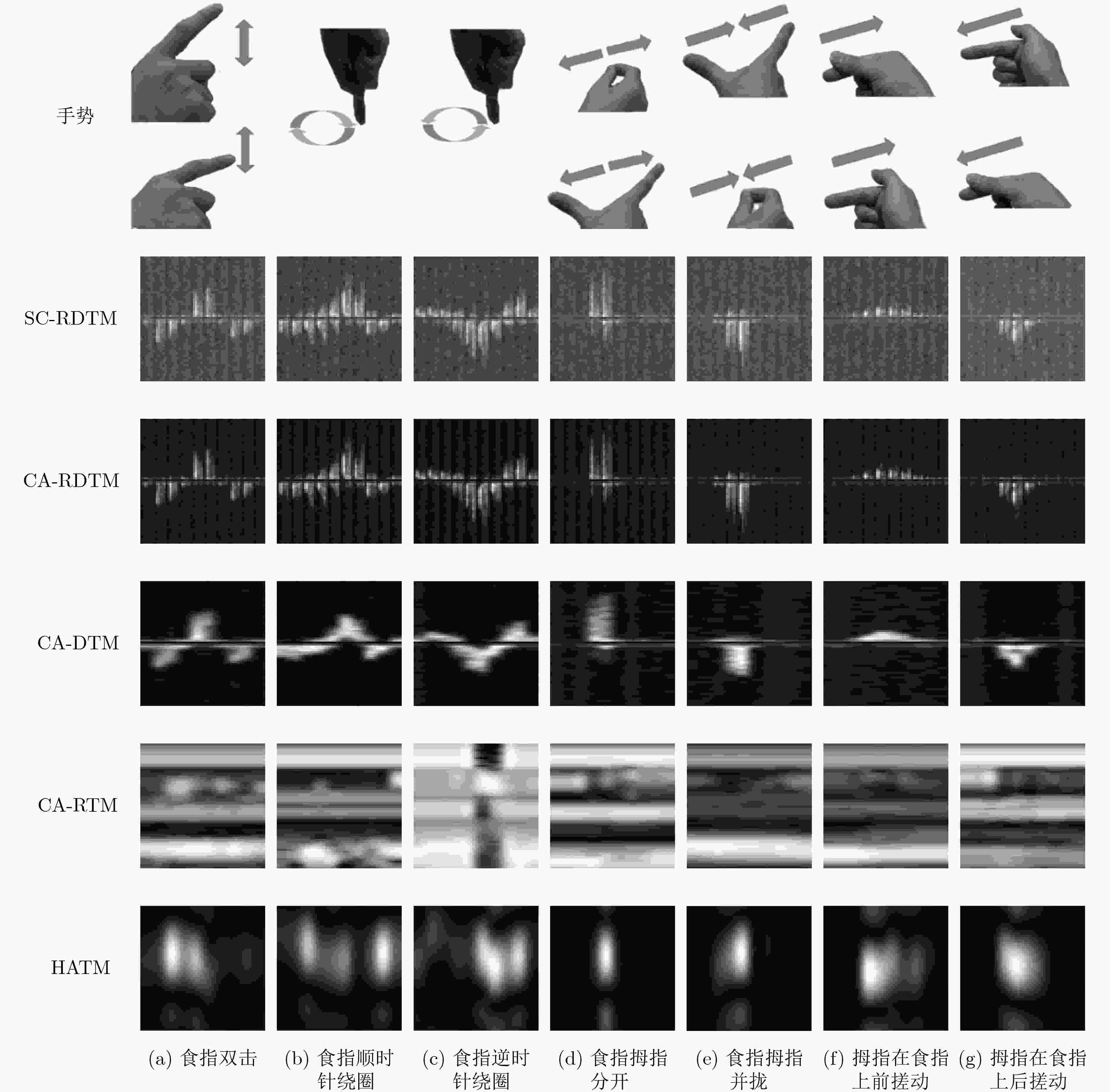
分类准确率(%)SC-RDTM 单通道CNN 98.28 CA-RDTM 单通道CNN 99.14 CA-DTM 单通道CNN 97.14 CA-RTM 单通道CNN 88.00 HATM 单通道CNN 71.71 CA-RTM, CA-DTM
与HATM联合3通道CNN 93.57 将包含2名测试对象，6种手势特征，7类手势各50张图像样本的手势数据集作为对象未经训练的测试集，分别用来测试6种手势特征对应的CNN分类模型的泛化能力，对7类微动手势的平均分类准确率如表3所示。
表 3 多种手势表征方法的对比特征类型 分类方法 测试对象A平均分类准确率(%) 测试对象B平均分类准确率(%) SC-RDTM 单通道CNN 86.00 84.29 CA-RDTM 单通道CNN 87.71 85.43 CA-DTM 单通道CNN 84.57 83.43 CA-RTM 单通道CNN 27.14 25.42 HATM 单通道CNN 34.28 30.57 CA-RTM, CA-DTM与HATM联合 3通道CNN 65.14 55.71 对比表2和表3可以看出，本文设计的通道平均距离-多普勒-时间图(CA-RDTM)特征对训练对象和测试对象的7类微动手势分类均能够获得最高的平均分类准确率，CA-RDTM特征优于SC-RDTM特征的原因是多通道平均能够有效提升雷达特征图像的信噪比(SNR)。为了定量对比两种特征的SNR，取图2中7类手势的CA-RDTM与SC-RDTM的第5帧(平均振幅最大的帧)中最大振幅和背景区域40个点的振幅均值的比值作为其SNR参照，如图3所示，手势类别索引1～7分别对应图2中(a)～(g)的7类手势，可以看出7类手势的RDTM特征经过8个通道的非相干叠加平均，能够提升2.5～4倍的信噪比。
单通道距离-多普勒-时间图(SC-RDTM)特征的平均分类准确率仅次于通道平均距离-多普勒-时间图(CA-RDTM)特征，两者分类表现差异不大，实际应用中可以综合考虑是否需要角度信息以及多通道的内存占用消耗来选择采用单通道还是通道平均。
CA-DTM特征取得了与RDTM特征接近的分类表现，明显优于CA-RTM与HATM特征，说明单独的DTM特征也能够比较有效地区分7类微动手势，是决定RDTM特征和多通道联合特征分类表现的主要特征，而融合了距离特征的RDTM特征能够进一步获得更好的分类表现，验证了融合的有效性。
单一的CA-RTM特征和HATM特征表现不佳，主要是因为微动手势的距离和角度变化不明显，而将微动手势表征能力差的CA-RTM特征和HATM特征与CA-DTM特征在CNN中进行通道融合会明显降低分类表现，说明这种融合方法不可取。
对比表2和表3中利用相同分类特征和分类方法对5名训练对象和2名测试对象的平均分类准确率可以看出，本文设计的分类特征和分类方法对训练集中有对应样本的训练对象的分类表现优异，但对训练集中没有对应样本的测试对象的分类表现不佳，说明模型的泛化能力还有进一步的提升空间，一方面可以考虑采集大量训练对象的样本进行训练，另一方面可以考虑改进CNN的结构和参数设计。
基于本文设计的CA-RDTM特征对5名训练对象和2名测试对象做的7类微动手势分类的混淆矩阵分别如表4、表5和表6所示。表4中，食指拇指并拢和拇指在食指上后搓动2类手势有一定程度混淆，是因为当2类手势的距离变化差异不大，且前者的运动速度较小时，2种手势的距离多普勒谱随时间变化过程比较近似；表5中，食指顺时针绕圈和食指逆时针绕圈2类手势的混淆程度较高，是因为这2类手势的定义规定了起始点为所绕圆圈的最右端，未经训练的测试对象在做这两类手势时，若起始点位置不合理，距离多普勒特征容易混淆。因此，在设计手势动作时应该考虑特征参数的相似性，在进行特征参数计算时可以考虑对分类特征相似的手势加入一些约束条件进行进一步区分。
表 4 7种微动手势分类的混淆矩阵预测类别 食指双击 食指顺时
针绕圈食指逆时
针绕圈食指拇
指分开食指拇
指并拢拇指在食指
上前搓动拇指在食指
上后搓动准确度(%) 真实类别 食指双击 100 0 0 0 0 0 0 100 食指顺时针绕圈 0 100 0 0 0 0 0 100 食指逆时针绕圈 0 0 100 0 0 0 0 100 食指拇指分开 0 0 0 100 0 0 0 100 食指拇指并拢 0 0 0 0 98 0 2 98 拇指在食指上前搓动 0 0 0 0 0 100 0 100 拇指在食指上后搓动 0 0 0 0 4 0 96 96 准确度(%) 100 100 100 100 96.08 100 97.96 99.14 表 5 测试对象A 7类微动手势分类的混淆矩阵预测类别 食指双击 食指顺时
针绕圈食指逆时
针绕圈食指拇
指分开食指拇
指并拢拇指在食指
上前搓动拇指在食指
上后搓动准确度(%) 真实类别 食指双击 46 3 1 0 0 0 0 92 食指顺时针绕圈 0 35 15 0 0 0 0 70 食指逆时针绕圈 3 13 34 0 0 0 0 68 食指拇指分开 0 0 0 49 0 1 0 98 食指拇指并拢 0 0 0 0 46 0 4 92 拇指在食指上前搓动 0 0 0 1 0 49 0 98 拇指在食指上后搓动 0 0 0 0 2 0 48 96 准确度(%) 93.88 68.63 68 98 95.83 98 92.31 87.71 表 6 测试对象B 7类微动手势分类的混淆矩阵预测类别 食指双击 食指顺
时针绕圈食指逆时
针绕圈食指拇
指分开食指拇
指并拢拇指在食指
上前搓动拇指在食指
上后搓动准确度(%) 真实类别 食指双击 45 2 3 0 0 0 0 90 食指顺时针绕圈 0 32 18 0 0 0 0 64 食指逆时针绕圈 1 16 33 0 0 0 0 66 食指拇指分开 0 0 0 46 0 4 0 92 食指拇指并拢 0 0 0 0 48 0 2 96 拇指在食指上前搓动 0 0 0 2 0 48 0 96 拇指在食指上后搓动 0 0 0 0 3 0 47 94 准确度(%) 97.83 64 61.11 95.83 94.12 92.31 95.92 85.43 4. 结论
本文提出了一种基于多通道FMCW毫米波雷达的微动手势识别方法，给出了能够有效表征微动手势的雷达参数设计方法。针对雷达特征图像设计了仅有3个卷积层和2个全连接层的轻量化卷积神经网络，利用SC-RDTM, CA-RDTM, CA-DTM, CA-RTM, HATM以及RTM、DTM与HATM联合等6种雷达特征对应的7类微动手势数据集进行训练和测试，并分别对5名包含在训练样本中的训练对象和2名未包含在训练样本中的测试对象进行分类。分类结果显示，相比其他特征，本文设计的距离-多普勒-时间图特征能够有效融合距离-时间和多普勒-时间特征，取得最优的分类表现，对5名训练对象的平均分类准确率为99.14%，对2名测试对象的平均分类准确率分别为87.71%和85.43%，证明本文提出的微动手势识别方法不仅具有更好的微动手势表征能力，而且具有较好的测试对象泛化能力。
-
表 2 多种手势表征方法的对比
特征类型 分类方法 5名训练对象平均
分类准确率(%)SC-RDTM 单通道CNN 98.28 CA-RDTM 单通道CNN 99.14 CA-DTM 单通道CNN 97.14 CA-RTM 单通道CNN 88.00 HATM 单通道CNN 71.71 CA-RTM, CA-DTM
与HATM联合3通道CNN 93.57 
下载: 导出CSV
表 3 多种手势表征方法的对比
特征类型 分类方法 测试对象A平均分类准确率(%) 测试对象B平均分类准确率(%) SC-RDTM 单通道CNN 86.00 84.29 CA-RDTM 单通道CNN 87.71 85.43 CA-DTM 单通道CNN 84.57 83.43 CA-RTM 单通道CNN 27.14 25.42 HATM 单通道CNN 34.28 30.57 CA-RTM, CA-DTM与HATM联合 3通道CNN 65.14 55.71
下载: 导出CSV
表 4 7种微动手势分类的混淆矩阵
预测类别 食指双击 食指顺时
针绕圈食指逆时
针绕圈食指拇
指分开食指拇
指并拢拇指在食指
上前搓动拇指在食指
上后搓动准确度(%) 真实类别 食指双击 100 0 0 0 0 0 0 100 食指顺时针绕圈 0 100 0 0 0 0 0 100 食指逆时针绕圈 0 0 100 0 0 0 0 100 食指拇指分开 0 0 0 100 0 0 0 100 食指拇指并拢 0 0 0 0 98 0 2 98 拇指在食指上前搓动 0 0 0 0 0 100 0 100 拇指在食指上后搓动 0 0 0 0 4 0 96 96 准确度(%) 100 100 100 100 96.08 100 97.96 99.14
下载: 导出CSV
表 5 测试对象A 7类微动手势分类的混淆矩阵
预测类别 食指双击 食指顺时
针绕圈食指逆时
针绕圈食指拇
指分开食指拇
指并拢拇指在食指
上前搓动拇指在食指
上后搓动准确度(%) 真实类别 食指双击 46 3 1 0 0 0 0 92 食指顺时针绕圈 0 35 15 0 0 0 0 70 食指逆时针绕圈 3 13 34 0 0 0 0 68 食指拇指分开 0 0 0 49 0 1 0 98 食指拇指并拢 0 0 0 0 46 0 4 92 拇指在食指上前搓动 0 0 0 1 0 49 0 98 拇指在食指上后搓动 0 0 0 0 2 0 48 96 准确度(%) 93.88 68.63 68 98 95.83 98 92.31 87.71
下载: 导出CSV
表 6 测试对象B 7类微动手势分类的混淆矩阵
预测类别 食指双击 食指顺
时针绕圈食指逆时
针绕圈食指拇
指分开食指拇
指并拢拇指在食指
上前搓动拇指在食指
上后搓动准确度(%) 真实类别 食指双击 45 2 3 0 0 0 0 90 食指顺时针绕圈 0 32 18 0 0 0 0 64 食指逆时针绕圈 1 16 33 0 0 0 0 66 食指拇指分开 0 0 0 46 0 4 0 92 食指拇指并拢 0 0 0 0 48 0 2 96 拇指在食指上前搓动 0 0 0 2 0 48 0 96 拇指在食指上后搓动 0 0 0 0 3 0 47 94 准确度(%) 97.83 64 61.11 95.83 94.12 92.31 95.92 85.43
下载: 导出CSV
-
WAN Qian, LI Yiran, LI Changzhi, et al. Gesture recognition for smart home applications using portable radar sensors[C]. The 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, USA, 2014: 6414–6417. KHAN F, LEEM S K, and CHO S H. Hand-based gesture recognition for vehicular applications using IR-UWB radar[J]. Sensors, 2017, 17(4): 833. doi: 10.3390/s17040833 XIA Zia, SANG Xinzhu, CHEN Duo, et al. An interactive VR system based on full-body tracking and gesture recognition[C]. The SPIE 10021, Optical Design and Testing VⅡ, Beijing, China 2016: 1002129. LEE B G and LEE S M. Smart wearable hand device for sign language interpretation system with sensors fusion[J]. IEEE Sensors Journal, 2018, 18(3): 1224–1232. doi: 10.1109/JSEN.2017.2779466 TARANTA Ⅱ E M, SIMONS T K, SUKTHANKAR R, et al. Exploring the benefits of context in 3D gesture recognition for game-based virtual environments[J]. ACM Transactions on Interactive Intelligent Systems, 2015, 5(1): Article No.1. BONATO V, FERNANDES M M, and MARQUES E. A smart camera with gesture recognition and SLAM capabilities for mobile robots[J]. International Journal of Electronics, 2006, 93(6): 385–401. doi: 10.1080/00207210600565465 孟春宁, 吕建平, 陈萱华. 基于普通红外摄像机的手势识别[J]. 计算机工程与应用, 2015, 51(16): 17–22. doi: 10.3778/j.issn.1002-8331.1504-0303MENG Chunning, LÜ Jianping, and CHEN Xuanhua. Gesture recognition based on universal infrared camera[J]. Computer Engineering and Applications, 2015, 51(16): 17–22. doi: 10.3778/j.issn.1002-8331.1504-0303 PLOUFFE G and CRETU A M. Static and dynamic hand gesture recognition in depth data using dynamic time warping[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(2): 305–316. doi: 10.1109/TIM.2015.2498560 YANG Qifan, TANG Hao, ZHAO Xuebing, et al. Dolphin: Ultrasonic-based gesture recognition on smartphone platform[C]. The 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 2014: 1461–1468. KELLOGG B, TALLA V, and GOLLAKOTA S. Bringing gesture recognition to all devices[C]. The 11th Usenix Conference on Networked Systems Design and Implementation, Seattle, USA, 2014: 303–316. ZOU Yongpan, XIAO Jiang, HAN Jinsong, et al. GRfid: A device-free RFID-based gesture recognition system[J]. IEEE Transactions on Mobile Computing, 2017, 16(2): 381–393. doi: 10.1109/TMC.2016.2549518 ABDELNASSER H, YOUSSEF M, and HARRAS K A. WiGest: A ubiquitous WiFi-based gesture recognition system[C]. Proceedings of IEEE Conference on Computer Communications, Hongkong, China, 2015: 1472–1480. ZHANG Jiajun, TAO Jinkun, and SHI Zhiguo. Doppler-radar based hand gesture recognition system using convolutional neural networks[C]. The 2017 International Conference on Communications, Signal Processing, and Systems, Singapore, 2019: 1096–1113. LIEN J, GILLIAN N, KARAGOZLER M, et al. Soli: Ubiquitous gesture sensing with millimeter wave radar[J]. ACM Transactions on Graphics, 2016, 35(4): Article No.142. WANG Saiwen, SONG Jie, LIEN J, et al. Interacting with Soli: Exploring fine-grained dynamic gesture recognition in the radio-frequency spectrum[C]. The 29th Annual Symposium on User Interface Software and Technology, Tokyo, Japan, 2016: 851–860. HAZRA S and SANTRA A. Robust gesture recognition using Millimetric-wave radar system[J]. IEEE Sensors Letters, 2018, 2(4): 7001804. MALYSA G, WANG Dan, NETSCH L, et al. Hidden Markov model-based gesture recognition with FMCW radar[C]. 2016 IEEE Global Conference on Signal and Information Processing, Washington, USA, 2016: 1017–1021. 王勇, 吴金君, 田增山, 等. 基于FMCW雷达的多维参数手势识别算法[J]. 电子与信息学报, 2019, 41(4): 822–829. doi: 10.11999/JEIT180485WANG YONG, WU Jinjun, TIAN Zengshan, et al. Gesture recognition with multi-dimensional parameter using FMCW radar[J]. Journal of Electronics &Information Technology, 2019, 41(4): 822–829. doi: 10.11999/JEIT180485 刘熠辰, 徐丰. 基于雷达技术的手势识别[J]. 中国电子科学研究院学报, 2016, 11(6): 609–613. doi: 10.3969/j.issn.1673-5692.2016.06.009LIU Yichen and XU Feng. Gesture recognition based on radar technology[J]. Journal of CAEIT, 2016, 11(6): 609–613. doi: 10.3969/j.issn.1673-5692.2016.06.009 期刊类型引用(29)
1. 张春杰，王冠博，陈奇，邓志安. 基于纯自注意力机制的毫米波雷达手势识别. 系统工程与电子技术. 2024(03): 859-867 . 
百度学术2. 赵雅琴，宋雨晴，吴晗，何胜阳，刘璞秋，吴龙文. 基于DenseNet和卷积注意力模块的高精度手势识别. 电子与信息学报. 2024(03): 967-976 . 
本站查看3. 许婷，饶云华，易建新. 基于半监督生成对抗网络的毫米波雷达跨域手势识别. 电子测量技术. 2024(04): 1-9 . 百度学术4. 刘秀兰，程林，周文斌，赵宇彤，孟颖，关宇. 基于调频连续波技术的充电系统智能故障定位方法. 电子器件. 2024(02): 436-441 . 百度学术5. 王潇怡，罗运华，喻忠军，孙浩，王晓蓓. 基于EfficientNet的多通道雷达目标微动特征分类方法. 系统工程与电子技术. 2024(09): 2988-2998 . 百度学术6. 林倩，杨姝玥，刘林盛. 浅析毫米波雷达在汽车电子中的应用. 天津理工大学学报. 2024(05): 80-85 . 百度学术7. 龚树凤，方一鸣，施汉银，闫鑫悦，吴哲夫. 基于深度学习的毫米波雷达手势识别实验教学设计. 实验技术与管理. 2023(04): 168-176 . 百度学术8. 许妍，常俊，吴彭，罗金燕，王义元. 基于毫米波雷达传感器RAI图像的手势识别方法. 电子测量技术. 2023(06): 15-22 . 百度学术9. 冯翔，刘涛，崔文卿，吴沐府，李风从，赵宜楠. 基于双视角时序特征融合的毫米波雷达手势数字识别研究. 电子与信息学报. 2023(06): 2134-2143 . 本站查看10. 李仕，卢俊阳，张明威，王航宁，王毅刚. 大场景下自由手势交互技术. 印刷与数字媒体技术研究. 2023(04): 244-251 . 百度学术11. 龚树凤，李棋斌，施汉银，林超，李翔. 基于小样本学习的毫米波雷达手势识别方法. 传感技术学报. 2023(08): 1235-1242 . 百度学术12. 陈君毅，蒋德琛，王智铭，曹佳禾，王勇. 一种基于双维度滤波和自适应定长化的FMCW雷达手势识别算法研究. 电子学报. 2023(08): 2179-2187 . 百度学术13. 魏军，韩君龙，王巍，左自辉. 基于毫米波雷达的铁路隧道人员定位技术研究. 隧道建设(中英文). 2023(S2): 223-229 . 百度学术14. 屈乐乐，张丁元，杨天虹，孙延鹏. 基于双频段FMCW雷达的人体动作识别. 电讯技术. 2022(01): 59-65 . 百度学术15. 韩崇，韩磊，孙力娟，郭剑. 基于时空压缩特征表示学习的毫米波雷达手势识别算法. 电子与信息学报. 2022(04): 1274-1283 . 本站查看16. 屈乐乐，张丁元，杨天虹，张丽丽，孙延鹏. 基于双流特征融合的FMCW雷达人体连续动作识别. 雷达科学与技术. 2022(05): 565-572 . 百度学术17. 屈乐乐，吴涵旭，杨天虹，孙延鹏. 基于双通道CNN的FMCW雷达手势识别方法. 电子器件. 2022(06): 1469-1475 . 百度学术18. 吴哲夫，邵承贤，龚树凤，毛科技，吕跃华. 基于信道状态特征的手势动作识别技术研究. 传感技术学报. 2021(01): 8-14 . 百度学术19. 谢垚，黄默，王长元，张圆圆，荆琛. 一种改进的宽波束线阵雷达物位测量算法. 西安电子科技大学学报. 2021(02): 165-172 . 百度学术20. 刘子铭，李军，张法桐，陈涛. 基于77G毫米波雷达的手势识别. 电子技术与软件工程. 2021(10): 55-58 . 百度学术21. 孙延鹏，艾俊，屈乐乐. 一种基于连续波雷达的手势识别方法. 电讯技术. 2021(07): 815-820 . 百度学术22. 严光君，陈万忠，张涛，蒋鋆，任水芳. 基于灰度理论模型的截肢受试者手势分类方法研究. 电子与信息学报. 2021(09): 2552-2560 . 本站查看23. 靳标，彭宇，邝晓飞，张贞凯. 基于串联式一维神经网络的毫米波雷达动态手势识别方法. 电子与信息学报. 2021(09): 2743-2750 . 本站查看24. 卢迪，马文强. 基于改进YOLOv4-tiny算法的手势识别. 电子与信息学报. 2021(11): 3257-3265 . 本站查看25. 陈涛，张法桐，刘子铭. 基于FMCW毫米波雷达手势识别. 应用科技. 2021(06): 23-27 . 百度学术26. 高波，许贤泽，陈潮升. 一种基于激光相位测距原理的重质原油液位测量方法. 激光杂志. 2021(12): 59-65 . 百度学术27. 李东阳，方建，刘勇，唐小宏. 一种Ka波段FMCW频率源的设计与实现. 微波学报. 2021(S1): 74-76 . 百度学术28. 李瑶，王欣，贺文涛，史宝岱. 基于随机森林的脉冲超宽带雷达微动手势识别. 激光与光电子学进展. 2021(22): 75-83 . 百度学术29. 张蒙蒙，代阳，杨鹏程，张敏，肖旭. 幻影成像装置的自然手势识别系统设计. 西安工程大学学报. 2020(05): 63-67 . 百度学术其他类型引用(28)
-
下载:
百度学术
计量
- 文章访问数: 4986
- HTML全文浏览量: 1557
- PDF下载量: 292
- 被引次数: 57
下载:
